Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Bibliography >>

$\textstyle \parbox{0.85\textwidth}{ \raggedleft {\bf V.~V.~Orlov, A.~V.~Petrova... ...~Rubinov}\\ Sankt-Peterburgskii gosudarstvennyi universitet\\ \raggedright }$

1


KRATNYE ZVEZDY:
FORMIROVANIE I EVOLYuCIYa


Soglasno sovremennym predstavleniyam (sm., naprimer, obzor Larsona [1]), bol'shinstvo odinochnyh i dvoinyh zvezd moglo sformirovat'sya pri raspade neierarhicheskih kratnyh zvezd. Takie ob'ekty obrazuyutsya pri fragmentacii yader molekulyarnyh oblakov (sm., naprimer, Klessen i dr. [2]). Nesmotrya na ogromnoe kolichestvo rabot po teorii zvezdoobrazovaniya i po nablyudeniyam oblastei zvezdoobrazovaniya, do sih por net kakoi-libo "standartnoi" modeli zvezdoobrazovaniya [1]. Po-vidimomu, formiruyushiesya malye gruppy zvezd obladayut shirokim diapazonom harakteristik (razmerov, dispersii skorostei, spektrov mass i t. d.).

Na nachal'noi stadii evolyucii takih sistem osnovnuyu rol' igrayut gazodinamicheskie processy, kotorye mozhno opisat' v ramkah SPH-shemy (sm., naprimer, obzor Bodenheimera i dr. [3], a takzhe stat'yu Monahana [4]). Drugoi effektivnyi podhod -- reshenie gidrodinamicheskih uravnenii metodom setok s ispol'zovaniem kratnyh setok ili adaptivnogo "rafinirovaniya" yacheek (AMR) (sm. ssylki v tom zhe obzore [3]). V AMR-sheme v dinamicheskom rezhime menyayutsya polozheniya i razmery setok, po mere neobhodimosti sozdayutsya novye setki i udalyayutsya nenuzhnye.

Chislennoe modelirovanie processa formirovaniya zvezdnyh sistem pokazyvaet, chto mogut obrazovyvat'sya sistemy razlichnoi kratnosti s harakternymi razmerami $ \sim 1-100$ a. e. V konce 60-h gg. proshlogo veka van Al'bada [5] predpolozhil, chto ustoichivye dvoinye i kratnye zvezdy mogli sformirovat'sya v rezul'tate dinamicheskogo raspada malyh zvezdnyh grupp, soderzhashih ot neskol'kih do neskol'kih desyatkov zvezd.

S drugoi storony, ierarhicheskie ustoichivye kratnye zvezdy takzhe mogut formirovat'sya iz vrashayushegosya gazopylevogo oblaka v rezul'tate fragmentacii (sm., naprimer, obzor [3]).

Dal'neishaya evolyuciya sistemy mozhet byt' opisana v ramkah gravitacionnoi zadachi $ N$ tel s uchetom ryada dopolnitel'nyh effektov -- sliyanii komponentov pri tesnyh sblizheniyah, prilivnyh vzaimodeistvii zvezd, poteri massy komponentami vsledstvie zvezdnogo vetra i vspyshechnoi aktivnosti. Primer dinamicheskoi evolyucii neierarhicheskoi sistemy $ N=6$ tel pokazan v sleduyushem fil'me. Zdes' my vidim sblizheniya, vybrosy i uhody zvezd, formirovanie dvoinyh podsistem. V finale evolyucii obrazuetsya dvoinaya ili ustoichivaya ierarhicheskaya troinaya sistema.

Chislennye eksperimenty (sm., naprimer, Sterzik i Durisen [6], Rubinov, Petrova i Orlov [7]) pokazyvayut, chto neierarhicheskie sistemy maloi kratnosti raspadayutsya na dinamicheski nesvyazannye podsistemy. Eto mogut byt' odinochnye zvezdy, dvoinye, ustoichivye ierarhicheskie troinye i, vozmozhno, sistemy bol'shei kratnosti. Rassmotrim raspredelenie sostoyanii kratnyh sistem s $ N=3,6,9,12,15,18$ i nachal'nym spektrom mass Solpitera na moment vremeni 300 $ T_{cr}$, gde $ T_{cr}$ -- srednee nachal'noe vremya peresecheniya komponentom sistemy (tabl. 1). Primerno v polovine sluchaev k etomu momentu evolyuciya sistemy zakanchivaetsya formirovaniem dvoinoi sistemy. Eshe primerno v 10-15% sluchaev obrazuetsya ustoichivaya troinaya sistema. Okolo 30% sistem k etomu momentu ne zavershili svoyu evolyuciyu.


Table: Raspredeleniya po sostoyaniyam pri $ t=300 T_{cr}$
  Dvoinye Dve Ustoich. Neustoich. Sistemy  
  sistemy odinochnyh troinye troinye s $ n \geq 4$  
$ 3$ $ 0.78$ - $ 0.01$ $ 0.21$ -  
$ 6$ $ 0.56$ $ 0.01$ $ 0.14$ $ 0.16$ $ 0.13$  
$ 9$ $ 0.55$ $ 0.03$ $ 0.16$ $ 0.14$ $ 0.12$  
$ 12$ $ 0.47$ $ 0.04$ $ 0.17$ $ 0.16$ $ 0.16$  
$ 15$ $ 0.49$ $ 0.06$ $ 0.13$ $ 0.15$ $ 0.17$  
$ 18$ $ 0.51$ $ 0.06$ $ 0.11$ $ 0.14$ $ 0.18$  

Interesno sopostavit' rezul'taty s funkciei kratnosti nablyudaemyh zvezd. Po katalogu 807 fizicheskih kratnyh sistem funkciyu kratnosti postroil Tokovinin [8]. On nashel otnosheniya chisla sistem raznoi kratnosti $ n$:

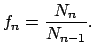
$\displaystyle f_n = {{N_n} \over {N_{n-1}}}. $


Table: Funkciya kratnosti
$ n$ 3 4 5 6
$ f_n$ 0.11 0.22 0.20 0.36
  3 2 4 14

Otmetim, chto otnoshenie $ f_n$ v predelah oshibok primerno postoyanno, nachinaya s $ n=4$, i sostavlyaet $ 0.26 \pm 0.05$. Pri perehode ot troinyh k dvoinym ono umen'shaetsya primerno vdvoe (tabl. 2).

Orlov i Titov [9] ocenili otnoshenie chisla zvezd, vhodyashih v sistemy kratnosti $ n=1,2,3, \geq 4$, dlya blizkih zvezd v predelah 25 pk ot Solnca kak $ 0.64:0.28:0.06:0.02$. Sootvetstvuyushie ocenki otnoshenii $ f_3 \approx 0.14$, $ f_4 \approx 0.25$ v predelah oshibok soglasuyutsya s dannymi Tokovinina [8]. Ocenka $ f_2 \approx 0.22$ dlya zvezd okrestnosti Solnca soglasuetsya s ocenkoi $ f_2 \approx 0.23$, poluchennoi dlya processa raspada malyh grupp zvezd.

Esli my predpolozhim, chto neustoichivye troinye sistemy v konechnom schete raspadayutsya s formirovaniem final'noi dvoinoi, to dolya final'nyh dvoinyh dostignet 70%. Sootvetstvuyushee otnoshenie $ f_3 \approx 0.2$ ne sil'no otlichaetsya ot ocenok, poluchennyh iz nablyudenii. Seichas my ne znaem, skol' chasto formiruyutsya ustoichivye sistemy s kratnost'yu $ n \geq 4$. Po-vidimomu, chast' sistem s $ n \geq 4$ neustoichivy i raspadayutsya za vremya, bol'shee 300 $ T_{cr}$, s obrazovaniem dvoinyh ili ustoichivyh troinyh sistem. Poetomu ocenka $ f_3 \approx 0.2$ nenadezhna.

Interesno opredelit' harakteristiki final'nyh ustoichivyh sistem i sravnit' ih s dannymi nablyudenii dvoinyh i troinyh zvezd.

Osnovnye harakteristiki dvoinyh zvezd -- bol'shaya poluos' i ekscentrisitet orbity. Pri nachal'nyh razmerah gruppy $ \sim 100$ a. e. bol'shie poluosi final'nyh i vybroshennyh dvoinyh sistem nahodyatsya v diapazone ot $ \sim 1$ do $ \sim 10^3$ a. e. Etot diapazon soglasuetsya s dannymi dlya shirokih dvoinyh (sm., naprimer, Dyukenua i Maior [10], Hikoks [11]). Bolee tesnye dvoinye v principe mogli sformirovat'sya pri dinamicheskom raspade bolee kompaktnyh grupp zvezd.

Raspredeleniya ekscentrisitetov dvoinyh, formiruyushihsya pri raspade sistem s kratnost'yu $ N=6$ i nachal'nym spektrom mass Solpitera, privedeny na ris. 1. Pryamaya sootvetstvuet zakonu  $ f(e) = 2e$, poluchennomu Ambarcumyanom [12] dlya ravnovesnogo raspredeleniya dvoinyh v zvezdnom pole. Takoe zhe raspredelenie polucheno v statisticheskoi teorii raspada troinyh sistem (sm. Monahan [13]).

Figure: Raspredeleniya ekscentrisitetov dvoinyh, sformirovavshihsya pri raspade sistem s $ N=6$. Belye stolbcy sootvetstvuyut final'nym dvoinym, serye -- uhodyashim dvoinym. Pryamaya sootvetstvuet zakonu $ f(e) = 2e$

Iz risunka vidno, chto rezul'taty chislennogo modelirovaniya soglasuyutsya s teoriei. Raspredeleniya ekscentrisitetov shirokih dvoinyh zvezd posle ucheta nablyudatel'noi selekcii takzhe soglasuyutsya s zakonom $ f(e) = 2e$ (sm., naprimer, Valtonen [14], Tokovinin [15]). Eto soglasovanie yavlyaetsya dopolnitel'nym argumentom v pol'zu dinamicheskogo proishozhdeniya shirokih dvoinyh.

Pereidem k rassmotreniyu ustoichivyh troinyh sistem. Ustoichivye troinye, obrazuyushiesya pri raspade malyh grupp, obladayut znachitel'noi ierarhiei -- srednee otnoshenie bol'shih poluosei orbit vneshnei i vnutrennei dvoinyh sostavlyaet primerno $ 20:1$, a srednee otnoshenie periodov -- priblizitel'no $ 70:1$.

Na ris. 2 predstavleny raspredeleniya ekscentrisitetov vnutrennih i vneshnih dvoinyh.

Figure: Raspredeleniya ekscentrisitetov vnutrennih (belye stolbiki) i vneshnih (serye stolbiki) dvoinyh v ustoichivyh troinyh. Sploshnaya liniya sootvetstvuet zakonu $ f(e) = 2e$

Iz risunka vidno, chto kak dlya vnutrennih, tak i dlya vneshnih par raspredeleniya ekscentrisitetov otlichayutsya ot zakona $ f(e) = 2e$. Nablyudaetsya deficit sil'no vytyanutyh orbit s $ e > 0.9$. Osobenno etot deficit zameten dlya vneshnih dvoinyh. Srednie znacheniya ekscentrisitetov sostavlyayut $ \overline {e_{in}} \approx 0.7$, $ \overline {e_{ex}} \approx 0.5$. Nami byla rassmotrena vyborka 38 ierarhicheskih troinyh zvezd s izvestnymi elementami orbit vnutrennei i vneshnei dvoinyh. Po etoi vyborke srednie znacheniya ekscentrisitetov $ \overline {e_{in}} \approx 0.37 \pm 0.04$, $ \overline {e_{ex}} \approx 0.38 \pm 0.04$. Eti znacheniya neskol'ko men'she velichin, poluchennyh dlya model'nyh sistem. Osobenno zametno razlichie dlya vnutrennih dvoinyh. Eto razlichie mozhet byt' svyazano s chastichnoi cirkulyarizaciei orbit vnutrennih dvoinyh iz-za prilivnogo vzaimodeistviya komponentov, kotoroe ne uchityvalos' pri chislennom modelirovanii. Krome togo, na rezul'tate mozhet skazat'sya selekciya -- trudnost' obnaruzheniya sil'no vytyanutyh sistem.

Eshe odna vazhnaya harakteristika struktury ierarhicheskih troinyh sistem -- otnositel'naya orientaciya orbit vnutrennei i vneshnei dvoinyh. V nashih modelyah s pervonachal'no izotropnym raspredeleniem skorostei v final'nyh ustoichivyh troinyh neskol'ko preobladayut sistemy s pryamymi dvizheniyami (ris. 3).

Figure: Raspredelenie uglov vzaimnogo naklona orbit vnutrennei i vneshnei dvoinyh (belye stolbiki). Serye stolbiki sootvetstvuyut sluchainoi orientacii orbit: $ f(i) = {1 \over 2} \sin i$

Analiz raspredeleniya $ f(i)$ dlya ustoichivyh troinyh, obrazuyushihsya pri raspade sistem s $ 3 \leq N \leq 10$ zvezd, byl vypolnen v rabote Sterzika i Tokovinina [16]. Rezul'tat zavisit ot geometrii sistemy, spektra mass, sootnosheniya mezhdu energiei vrasheniya i energiei sluchainyh dvizhenii komponentov. Dlya sluchaev s blizkimi k izotropnomu raspredeleniyami nachal'nyh skorostei final'nye troinye pokazyvayut umerennoe, no znachimoe preobladanie pryamyh dvizhenii so srednimi znacheniyami ugla mezhdu vektorami orbital'nyh momentov vneshnei i vnutrennei par $ \bar i \approx 70^\circ -80^\circ$. Dlya nablyudaemyh 22 troinyh sistem s izvestnymi elementami orbit vnutrennei i vneshnei dvoinyh (odnako s neopredelennost'yu dolgot voshodyashih uzlov) poluchena usrednennaya ocenka ugla $ \bar i = 79^\circ \pm 6^\circ$. Eta ocenka poluchena po smesi vernyh i lozhnyh uglov. Tem ne menee vidny yavnaya nekomplanarnost' orbit i tendenciya k preobladaniyu sistem s pryamymi dvizheniyami. Eta ocenka soglasuetsya i s rezul'tatami nashih chislennyh eksperimentov [7].

Nami byli vypolneny chislennye eksperimenty s drugim nachal'nym spektrom mass, menee krutym, chem spektr mass Solpitera. Takzhe byli rassmotreny raznye nachal'nye razmery sistem -- ot 3 do 1000 a. e. i raznye nachal'nye znacheniya virial'nogo otnosheniya -- ot 0.001 do 0.9.

Vyyasnilos', chto imeyutsya nekotorye invariantnye svoistva final'nyh sistem

  1. Vysokaya dolya ustoichivyh troinyh (10-15%).

  2. Universal'nost' raspredeleniya ekscentrisitetov final'nyh i uhodyashih dvoinyh $ f(e) = 2e$.

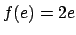  3. Znachitel'naya ierarhiya final'nyh troinyh.

  4. Vneshnie dvoinye imeyut menee vytyanutye orbity, chem vnutrennie.

  5. Preobladanie troinyh sistem s pryamymi dvizheniyami.

Na dinamicheskuyu evolyuciyu kratnyh zvezd mogut vliyat' nekotorye dopolnitel'nye faktory, v chastnosti:

1) dinamicheskoe trenie zvezd o mezhzvezdnuyu sredu,

2) poterya massy zvezdami,

3) prilivnoe vzaimodeistvie zvezd pri tesnyh sblizheniyah.

Nami byli rassmotreny pervye dva effekta. Dlya realistichnyh ocenok plotnosti mezhzvezdnoi sredy i tempa poteri massy rezul'taty okazyvayutsya prakticheski temi zhe, chto i bez ucheta etih effektov.

Poterya massy za schet zvezdnogo vetra skazyvaetsya na dinamicheskoi evolyucii shirokih kratnyh sistem s harakternymi nachal'nymi razmerami $ \sim 10^3$ a. e. Final'nye dvoinye i troinye stanovyatsya v srednem bolee shirokimi. Pri etom vneshnie dvoinye v ustoichivyh troinyh sistemah v srednem stanovyatsya bolee vytyanutymi.

Teper' rassmotrim evolyuciyu dvoinyh i ierarhicheskih troinyh sistem, kotorye mogut formirovat'sya kak pri raspade malyh grupp, tak i pri fragmentacii vrashayushegosya protozvezdnogo oblaka.

Shirokie dvoinye sistemy sohranyayut stabil'nost', esli oni dostatochno izolirovany ot zvezd polya. V tesnyh dvoinyh s obmenom veshestvom mezhdu komponentami vozmozhno sliyanie zvezd. V rezul'tate obrazuyutsya ob'ekty, kotorye nazyvayutsya golubymi brodyagami. V bolee shirokih dvoinyh prilivnoe vzaimodeistvie komponentov privodit k cirkulyarizacii orbit, sinhronizacii vrasheniya komponentov s orbital'nym dvizheniem i ortogonalizacii osei vrasheniya zvezd k ploskosti orbity.

Prilivnoe vzaimodeistvie zvezd, poterya massy i obmen veshestvom mezhdu komponentami mogut povliyat' na dinamicheskuyu evolyuciyu ierarhicheskih troinyh sistem, nahodyashihsya vblizi granicy ustoichivosti.

Okazalos' (sm. Orlov i Petrova [17]), chto vliyanie prilivov na izmenenie parametrov ustoichivosti troinyh sistem zavisit ot vrasheniya zvezd. Esli rotacionnye skorosti zvezd prevyshayut sinhronizovannye s orbital'nym dvizheniem, to zapas ustoichivosti troinoi sistemy umen'shaetsya. V protivnom sluchae on vozrastaet.

Effekt poteri massy posredstvom zvezdnogo vetra neskol'ko slozhnee. Zdes' sleduet rassmotret' dva scenariya narusheniya ustoichivosti troinoi sistemy:

  1. Obmen komponentami -- narushenie ierarhicheskoi struktury sistemy.

  2. Uhod udalennogo komponenta bez predshestvuyushego narusheniya ierarhii.

Okazalos' (Orlov, Petrova i Ivanova [18]), chto poterya massy zvezdami privodit k povysheniyu zapasa ustoichivosti troinoi sistemy po otnosheniyu k narusheniyu ierarhii. Chto kasaetsya uhoda udalennoi zvezdy bez narusheniya ierarhii, to rezul'tat zavisit ot otnosheniya mass komponentov. Esli massa udalennogo komponenta men'she, chem summarnaya massa vnutrennei dvoinoi, to imeet mesto tendenciya k potere ustoichivosti. V protivnom sluchae nablyudaetsya uvelichenie zapasa ustoichivosti. Sleduet otmetit', chto harakternye vremena izmeneniya mery ustoichivosti sravnimy s evolyucionnymi vremenami komponentov.

Mozhno rassmotret' takzhe effekt obmena veshestvom v tesnoi pare (Petrova [19]). Izmenenie zapasa ustoichivosti zavisit ot togo, kakoi iz komponentov tesnoi pary teryaet veshestvo. Esli massu teryaet bolee massivnyi komponent pary, to dvoinaya stanovitsya bolee tesnoi i zapas ustoichivosti troinoi sistemy uvelichivaetsya. Esli massu teryaet bolee legkii komponent pary, to dvoinaya stanovitsya shire i zapas ustoichivosti umen'shaetsya. Gravitacionnye vozmusheniya so storony tret'ego udalennogo komponenta privodyat k nekotorym neregulyarnostyam v zavisimostyah izmenenii parametrov ustoichivosti so vremenem - zavisimosti chasto imeyut vid stupenek. Naibolee sil'nye izmeneniya parametrov ustoichivosti proishodyat vblizi pericentra vneshnei dvoinoi.

V zaklyuchenie zametim, chto v principe pri fragmentacii gazovyh oblakov mogut formirovat'sya kak neierarhicheskie dinamicheski neustoichivye, tak i ierarhicheskie ustoichivye kratnye sistemy. V pervom sluchae sistema raspadaetsya na ustoichivye dvoinye i kratnye podsistemy i odinochnye zvezdy. Vremya raspada obychno na neskol'ko poryadkov velichiny koroche evolyucionnyh vremen komponentov. Vo vtorom sluchae dinamicheskaya evolyuciya protekaet znachitel'no medlennee - harakternye vremena sravnimy s evolyucionnymi vremenami komponentov.

Dlya dal'neishih rabot v etom napravlenii trebuetsya, s odnoi storony, nakoplenie nadezhnogo statisticheskogo materiala dlya troinyh zvezd i zvezd bol'shei kratnosti s izvestnymi orbitami vnutrennei i vneshnei par (osobenno ocenki vzaimnogo naklona orbit), a s drugoi storony, neobhodimy dostatochno ''rafinirovannye'' chislennye modeli dinamiki malyh grupp zvezd, a takzhe algoritmy ob'ektivnogo sravneniya modelei i nablyudenii.



Bibliography >>

Publikacii s klyuchevymi slovami: kratnye sistemy - dvoinye zvezdy - dvoinye sistemy - troinye sistemy - troinye zvezdy
Publikacii so slovami: kratnye sistemy - dvoinye zvezdy - dvoinye sistemy - troinye sistemy - troinye zvezdy
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 2.3 [golosov: 46]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya