Astronet > Fizicheskie voprosy teorii zvezdnoi evolyucii

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< Predislovie | Oglavlenie | 2. Relyativistskii gaz s vyrozhdeniem >>

Chast' I. FIZIKA ZVEZDNO' MATERII

Glava 1. Termodinamicheskie svoistva veshestva

Razdely

Veshestvo bol'shinstva zvezd imeet vysokuyu temperaturu i sravnitel'no umerennuyu plotnost'. V etih usloviyah kineticheskaya energiya chastic mnogo bol'she energii vzaimodeistviya mezhdu nimi i model' nerelyativistskogo, nevyrozhdennogo ideal'nogo gaza okazyvaetsya horoshim priblizheniem k real'nosti. Termodinamicheskie svoistva veshestva planet, naprimer. Zemli, izucheny gorazdo huzhe. Temperatura ih pri toi zhe plotnosti znachitel'no nizhe i veshestvo nahoditsya v zhidkoi i tverdoi fazah, issledovanie kotoryh sopryazheno s sushestvennymi trudnostyami.

V nedrah zvezd veshestvo i izluchenie nahodyatsya v termodinamicheskom ravnovesii, kotoroe ustanavlivaetsya bystrymi processami stolknovenii chastic, poglosheniem i ispuskaniem fotonov. Izluchenie, naryadu s gazom, sozdaet davlenie, protivodeistvuyushee sile tyazhesti.

Veshestvo zvezd sostoit iz razlichnyh himicheskih elementov, osnovnymi iz kotoryh yavlyayutsya vodorod i gelii. Na Solnce, naprimer, oni sostavlyayut v summe bolee 98,5% plotnosti veshestva. Ostal'naya chast' massy Solnca sostoit iz smesi prakticheski vseh stabil'nyh izotopov tablicy Mendeleeva. V tabl. 1 ukazano soderzhanie naibolee obil'nyh elementov, nablyudaemyh na Solnce [5]. Pri izmenenii ot centra do poverhnosti zvezdy temperatury na tri-chetyre poryadka i plotnosti na ~ 10 poryadkov izmenyaetsya sostoyanie ionizacii veshestva.

V central'nyh oblastyah zvezd s $\emph{M} \geq \emph{M}_{\odot }$ vse atomy prakticheski polnost'yu ionizovany.

Pust' $i$ - nomer himicheskogo elementa, kotoryi mozhet nahodit'sya v razlichnyh sostoyaniyah ionizacii ot neitral'nogo ( $j=0$ ) do polnost'yu ionizovannogo ( $j=i$ ). Oboznachim cherez $\epsilon_{\textrm{ij}}$ energiyu svyazi $j$ -kratno ionizovannogo iona elementa $i$ , opredelyaemuyu tak, chto dlya polnost'yu ionizovannogo iona $\epsilon_{\textrm{ij}}$ = 0. Udel'naya energiya E (erg g^-1), davlenie R (din sm^-2) i udel'naya entropiya S (erg g^-1 K^-1) dannoi smesi atomov, ionov i elektronov s izlucheniem imeyut vid [145] .

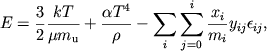
$%\begin{displaymath} %E=\frac{3}{2}\frac{kT}{\mu m_{u}}+\frac{aT^{4}}{\rho }-\Sigma _{i}\Sigma ^{i}_{j=0}\frac{x_{i}}{m_{i}}y_{ij}\epsilon _{ij} \end{displaymath} E={3\over2}{kT\over\mu m_{\rm u}}+ {\alpha T^4\over\rho}- \sum_i \sum_{j=0}^i {x_i\over m_i} y_{ij} \epsilon_{ij},$

(1.1)

$%\begin{displaymath}P=\frac{\rho kT}{\mu m_{u}}+\frac{1}{3}aT^{4} \end{displaymath} P = {\rho k T\over\mu m_{\rm u}}+{1\over 3}\alpha T^4,$

(1.2)

$%\begin{displaymath}S=\frac{k}{\rho }\Sigma _{i}\Sigma _{j=0}^{i}n_{ij}\left\{ \frac{5}{2}+\ln\left[ \left( \frac{m_{i}kT}{2\pi \hbar ^{2}}\right) ^{3/2}\frac{g_{ij}}{n_{ij}}\right] \right\} +\frac{k}{\rho }n_{e}\left\{ \frac{5}{2}+\ln\left[ \left( \frac{m_{e}kT}{2\pi \hbar }\right) ^{3/2}\frac{2}{n_{e}}\right] \right\} +\frac{4}{3}\frac{aT^{3}}{\rho } \end{displaymath} \eqalign{ S&={k\over\rho}\sum_i \sum_{j=0}^i n_{ij}\left\{ {5\over 2} \ln\left[ \left(m_i k T\over 2\pi \hbar^2\right)^{3/2} {g_{ij}\over n_{ij}}\right]\right\}\cr &\qquad+{k\over \rho} n_{\rm e} \left\{ {5\over 2}+\ln\left[ \left(m_{\rm e} k T\over 2\pi \hbar^2\right)^{3/2} {2\over n_{\rm e}} \right]\right\} +{4\over 3} {a T^3\over \rho},\cr }$

(1.3)

Zdes' ispol'zovany oboznacheniya:

$\rho$ - plotnost',

$T$ - temperatura,

$k=1.38067\cdot 10^{-16}\mbox{~erg}\cdot \mbox{K}^{-1}$ - postoyannaya Bol'cmana,

$\hbar =1.0546\cdot 10^{-27}\mbox{~erg}\cdot \mbox{s}$ - postoyannaya Planka,

$a=\pi ^{2}k^{4}/15\hbar ^{3}c^{3}=7.565\cdot 10^{-15}\mbox{~erg}\cdot \mbox{sm}^{-3}\cdot \mbox{K}^{-4}$ - postoyannaya plotnosti izlucheniya,

$c=2.9979\cdot 10^{10}\mbox{~sm}\cdot \mbox{s}^{-1}$ - skorost' sveta v vakuume,

$x_{ij}$ - massovaya dolya elementa s atomnym nomerom i,

Tablica 1. Rasprostranennost' naibolee obil'nyh himicheskih elementov (Solnce, [5])

Element	Simvol	Atomnyi nomer	Atomnaya massa	Desyatichnyi logarifm rasprostranennosti
Element	Simvol	Atomnyi nomer	Atomnaya massa	po chislu atomov	po masse
Vodorod	H	1	1.0080	12.00	12.00
Gelii	He	2	4.0026	10.93	11.53
Uglerod	C	6	12.0111	8.52	9.60
Azot	N	7	14.0067	7.96	9.11
Kislorod	O	8	15.9994	8.82	10.02
Neon	Ne	10	20.179	7.92	9.22
Natrii	Na	11	22.9898	6.25	7.61
Magnii	Mg	12	24.305	7.42	8.81
Alyuminii	Al	13	26.9815	6.39	7.78
Kremnii	Si	14	28.086	7.52	8.97
Fosfor	P	15	30.9738	5.52	7.01
Sera	S	16	32.06	7.20	8.71
Hlor	Cl	17	35.453	5.6	7.2
Argon	Ag	18	39.948	6.8	8.4
Kal'cii	Sa	20	40.08	6.30	7.90
Hrom	Sg	24	51.996	5.85	7.57
Marganec	Mn	25	54.9380	5.40	7.14
Zhelezo	Fe	26	55.847	7.60	9.35
Nikel'	Ni	28	58.71	6.30	8.07
Otnositel'noe soderzhanie po masse:			Chislo nuklonov na yadro,
Vodorod		X $_{\textrm{H}}$ =0.73	$\mu$ $_{\textrm{n}}$ =1.26
Gelii		X $_{\textrm{He}}$ =0.25	Srednyaya atomnaya massa pri polnoi ionizacii
Prochie elementy		$\Sigma$ x $_{\textrm{i}}$ =0.017	$\mu$ =0.60

$y_{ij}$ - stepen' $j$ -kratnoi ionizacii $j$ -go elementa, tak chto $\sum _{j=0}^{i}y_{ij}=1$ ,

$m_{i}\approx A_{i}m_{u}$ - massa yadra atoma s nomerom $i$ i atomnoi massoi $A_{i}\geq 4$

$m_{u}=1.66057\cdot 10^{-24}$ g - atomnaya edinica massy, ravnaya 1/12 massy izotopa $^{12}C$ ,

$m_{e}=9.10953\cdot 10^{-28}$ g - massa elektrona¹,

$%\begin{displaymath}n_{ij}=x_{i}\rho y_{ij}/m_{i} \mbox{~sm}^{-3} \end{displaymath} n_{ij}=x_i \rho y_{ij}/m_i \mbox{\rm~cm}^{-3}$

(1.4)

- koncentraciya ionov elementa $i$ v $j$ -m sostoyanii ionizacii,

$g_{ij}$ - statisticheskii ves iona $i$ -go elementa v $j$ -m sostoyanii ionizacii,

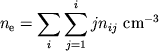$%\begin{displaymath}n_{e}=\Sigma _{i}\Sigma _{j=1}^{i}jn_{ij} \mbox{~sm}^{-3} \end{displaymath} n_{\rm e}=\sum_i \sum_{j=1}^i jn_{ij} \mbox{\rm~cm}^{-3}$

(1.5)

- koncentraciya elektronov v usloviyah elektroneitral'nosti,

$%\begin{displaymath}\mu =\left[ \Sigma _{i}\frac{m_{u}}{m_{i}}x_{i}\Sigma ^{i}_{j=0}(1+j)y_{ij}\right] ^{-1} \end{displaymath} \mu=\left[\sum_i {m_{\rm u}\over m_i} x_i \sum_{j=0}^i(1+j) y_{ij} \right]^{-1}$

(1.6)

- kolichestvo nuklonov na odnu chasticu gaza (srednyaya atomnaya massa).

V polnost'yu ionizovannom gaze, sostoyashem iz vodoroda, geliya i drugih elementov s $A_{i}\approx 2i\gg 1$ , imeem

$%\begin{displaymath} %\mu =\left[ 2x_{H}+\frac{3}{4}x_{He}+\frac{1}{2}x_{A}\right] ^{-1},~ %x_{A}=\Sigma _{i\geq 6}x_{i} ,~ %m_{He}\approx 4m_{u} ,~ %m_{H}\approx m_{u} \end{displaymath} \eqalign{ &\mu\simeq\left[2x_{\rm H}+{3\over 4}x_{\rm He}+{1\over 2} x_A\right]^{-1}, \qquad x_A=\sum\limits_{i\ge 6}x_i, \cr &m_{\rm He}\approx 4 m_{\rm u}, \quad m_{\rm H}\approx m_{\rm u}. \cr}$

(1.7)

Energiya v (1.1) otschityvaetsya ot energii pokoya polnost'yu ionizovannyh ionov i elektronov. Stepeni ionizacii elementov v termodinamicheskom ravnovesii opredelyayutsya formuloi Saha [145]

$%\begin{displaymath}\frac{y_{i,j-1}}{y_{i,j}}=n_{e}\frac{g_{i,j-1}}{2g_{ij}}\left( \frac{2\pi \hbar ^{2}}{m_{e}kT}\right) ^{3/2}e^{^{I_{ij}/kT}}=n_{e}K(T) . \end{displaymath} {y_{i,j-1}\over y_{ij}}=n_{\rm e}{g_{i,j-1}\over 2g_{ij}}\left( 2 \pi \hbar^2\over m_{\rm e}kT \right)^{3/2} e^{I_{ij}/kT}=n_{\rm e} K(T)$

(1.8)

Zdes' $I_{ij}=\epsilon _{i,j-1}-\epsilon _{ij}$ - energiya (potencial) ionizacii $i$ -go elektrona, $I_{i0}=0$ . Energii ionizacii naibolee obil'nyh elementov privedeny v tabl. 2. Dlya nahozhdeniya stepeni ionizacii elementov v smesi neobhodimo reshit' sistemu uravnenii (1.8) s uchetom (1.4), (1.5). Analiticheskoe re shenie poluchaetsya v sluchae odnokratnoi ionizacii odnogo ( $i$ -go) sorta atomov

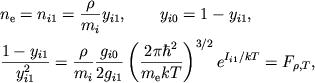
$\eqalign{ &n_{\rm e}=n_{i1}={\rho\over m_i} y_{i1}, \qquad y_{i0}=1-y_{i1}, \cr &{1-y_{i1}\over y_{i1}^2}={\rho\over m_i}{g_{i0}\over 2g_{i1}} \left( 2 \pi \hbar^2\over m_{\rm e}kT \right)^{3/2} e^{I_{i1}/kT}= F_{\rho,T}, \cr}$

otkuda

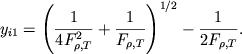$%\begin{displaymath}y_{i1}=\left( \frac{1}{4F_{\rho ,T}^{2}}+\frac{1}{F_{\rho ,T}}\right) ^{1/2}-\frac{1}{2F_{\rho ,T}}.\end{displaymath} y_{i1}=\left({1\over 4F_{\rho,T}^2}+{1\over F_{\rho,T}}\right)^{1/2} -{1\over 2F_{\rho,T}}.$

(1.9)

Tablica 2. Potencialy ionizacii i polnye momenty vneshnih elektronnyh obolochek naibolee obil'nyh elementov [180].

Atomnyi nomer	Element	Potencialy ionizacii, eV	Polnye momenty
1	H $^{-}$ ,H	0.747; 13.5985	0; 1/2
2	He	24.5876; 54.418	0; 1/2; 0
6	C	11.260; 24.284; 47.89; 64.49	0; 1/2; 0; 1/2
7	N	14.534; 29.602; 47.45; 77.47	3/2; 0; 1/2; 0
8	O	13.618; 35.118; 54.94; 77.41	2; 3/2; 0; 1/2
10	Ne	21.565; 40.964; 63.46; 97.12	0; 3/2; 2; 3/2
11	Na	5.1391; 47.287; 71.64; 98.92	1/2; 0; 3/2; 2
12	Mg	7.646; 15.035; 80.15; 109.2	0; 1/2; 0; 3/2
13	Al	5.9858; 18.828; 28.448; 120	1/2; 0; 1/2; 0
14	Si	8.152; 16.346; 33.493; 45.14	0; 1/2; 0; 1/2
15	P	10.49; 19.73; 30.18; 51.47	3/2; 0; 1/2; 0
16	S	10.36; 23.33; 34.83; 47.31	2; 3/2; 0; 1/2
17	Cl	12.968; 23.81; 39.61; 53.47	3/2; 2; 3/2; 0
18	Ar	15.760; 27.63; 40.74; 59.81	0; 3/2; 2; 3/2
20	Ca	6.113; 11.872; 50.91; 67.10	0; 1/2; 0; 3/2
24	Cr	6.766; 16.50; 30.96; 49	3; 5/2; 0; 3/2
25	Mn	7.4368; 15.640; 33.67; 51.2	5/2; 2; 5/2; 0
26	Fe	7.87; 16.18; 30.65; 54.8	4; 9/2 4; 5/2
28	Ni	7.63; 18.17; 35.2; 54.9	4; 5/2; 4; 9/2
1 eV = 11.604 K		X $_{0}$ ; X $_{+}$ ; X $_{++}$ ; X $_{+++}$	X $_{0}$ ; X $_{+}$ ; X $_{++}$ ; X $_{+++}$

Pri issledovanii zvezdnoi evolyucii chasto neobhodimo znat' znacheniya adiabaticheskih pokazatelei

$\gamma_1=\left(\partial\ln P\over \partial\ln\rho\right)_S, \quad \gamma_2=\left(\partial\ln T\over \partial\ln P\right)_S, \quad \gamma_3=\left(\partial\ln T\over \partial\ln\rho\right)_S,$

i teploemkostei

$%\begin{displaymath} %c_{\upsilon }=T\left( \frac{\partial S}{\partial T}\right) _{\rho } , \quad %c_{p}=\left( \frac{\partial S}{\partial T}\right) _{P}. %\end{displaymath} c_v=T\left(\partial S\over \partial T\right)_\rho,\quad c_p=T\left(\partial S\over \partial T\right)_P.$

V usloviyah nepolnoi ionizacii vse velichiny rasschityvayutsya chislenno, dlya chego ih udobno vyrazit' cherez proizvodnye

$%\begin{displaymath}\left( \frac{\partial \ln P}{\partial \ln\rho }\right) _{T} ,~ \left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho },~ %\left( \frac{\partial S}{\partial \ln\rho }\right) _{T} ,~ \left( \frac{\partial S}{\partial \ln T}\right) _{\rho }=c_{\upsilon }. \end{displaymath} \left(\partial\ln P\over \partial\ln\rho \right)_T,\quad \left(\partial\ln P\over \partial\ln T \right)_\rho,\quad \left(\partial S\over \partial\ln\rho\right)_T, \quad \left(\partial S\over \partial\ln T\right)_\rho=c_v.$

Vospol'zuemsya izvestnymi svoistvami yakobianov

$%\begin{displaymath}\frac{\partial (u,\upsilon )}{\partial (x,y)}=\frac{\partial (u,\upsilon )}{\partial (t,s)}\frac{\partial (t,s)}{\partial (x,y)} ; \quad %\frac{\partial (u,\upsilon )}{\partial (x,\upsilon )}=\left( \frac{\partial u}{\partial x}\right) _{\upsilon }. \end{displaymath} {\partial (u,v)\over \partial (x,y)} = {\partial (u,v)\over \partial (t,s)}{\partial (t,s)\over \partial (x,y)};\quad {\partial (u,v)\over \partial (x,v)} = \left(\partial u\over \partial x\right)_v,$

(1.10)

Poluchaem

$%\begin{displaymath}\gamma _{1}=\left( \frac{\partial \ln P}{\partial \ln\rho }\right) _{T}-\left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }\left( \frac{\partial S}{\partial \ln\rho }\right) _{T}\left/\left( \frac{\partial S}{\partial \ln T}\right)\right. _{\rho } , \end{displaymath} \gamma_1=\left(\partial\ln P\over \partial\ln\rho \right)_T- \left(\partial\ln P\over \partial\ln T \right)_\rho \left(\partial S\over \partial\ln\rho\right)_T \bigg/ \left(\partial S\over \partial\ln T\right)_\rho,$

(1.11)

$%\begin{displaymath}\gamma _{2}=\left[ \left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }-\left( \frac{\partial \ln P}{\partial \ln\rho }\right) _{T}\left( \frac{\partial S}{\partial \ln T}\right) _{\rho }\left/\left( \frac{\partial S}{\partial \ln\rho }\right)\right. _{T}\right] ^{-1}, \end{displaymath} \gamma_2=\left[\left(\partial\ln P\over \partial\ln T\right)_\rho- \left(\partial\ln P\over \partial\ln\rho \right)_T \left(\partial S\over \partial\ln T\right)_\rho \bigg/ \left(\partial S\over \partial\ln\rho\right)_T\right]^{-1},$

(1.12)

$%\begin{displaymath}\gamma _{3}=-\left( \frac{\partial S}{\partial \ln\rho }\right) _{T}\left/\left( \frac{\partial S}{\partial \ln T}\right)\right. _{\rho }, \end{displaymath} \gamma_3= -\left(\partial S\over \partial\ln\rho\right)_T \bigg/ \left(\partial S\over \partial\ln T\right)_\rho,$

(1.13)

$%\begin{displaymath}c_{\upsilon }=(\partial S/\partial \ln T)_{\rho }, \end{displaymath} c_v=\left(\partial S/\partial \ln T \right)_\rho,$

(1.14)

$%\begin{displaymath}c_{p}=c_{\upsilon }-\left( \frac{\partial S}{\partial \ln\rho }\right) _{T}\left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }\left/\left( \frac{\partial \ln P}{\partial \ln\rho }\right)\right. _{T}, \end{displaymath} c_p=c_v-\left(\partial S\over \partial\ln\rho\right)_T \left(\partial\ln P\over \partial\ln T \right)_\rho \bigg/ \left(\partial \ln P\over \partial\ln\rho\right)_T,$

(1.15)

$%\begin{displaymath}c_{p}/c_{\upsilon }=\gamma \left/\left( \frac{\partial \ln P}{\partial \ln\rho }\right)\right. _{T}. \end{displaymath} c_p/c_v=\gamma_1 \bigg/ \left(\partial \ln P\over \partial\ln\rho\right)_T.$

(1.16)

Proizvodnye ot entropii vyrazhayutsya cherez proizvodnye ot energii i davleniya iz pervogo zakona termodinamiki i usloviya polnoty differenciala svobodnoi energii $F=E-TS$ :

$%\begin{displaymath} %\left( \frac{\partial S}{\partial \ln T}\right) _{\rho }=\frac{1}{T}\left( \frac{\partial E}{\partial \ln T}\right) _{\rho }, \quad %\left( \frac{\partial S}{\partial \ln \rho }\right) _{T}=-\frac{1}{\rho T}\left( \frac{\partial P}{\partial \ln T}\right) _{T}. %\end{displaymath} \left(\partial S\over \partial\ln T\right)_\rho= {1\over T}\left(\partial E\over \partial\ln T\right)_\rho,\quad \left(\partial S\over \partial\ln\rho \right)_T= -{1\over\rho T}\left(\partial P\over \partial\ln T\right)_\rho.$

(1.17)

Esli stepeni ionizacii $y_{ij}$ postoyanny, to iz (1.3)-(1.6) slededuet

$%\begin{displaymath}S=\frac{k}{\mu m_{u}}\ln \left( T^{3/2}/\rho \right) +\frac{4}{3}\frac{aT^{3}}{\rho }+const \end{displaymath} S={k\over \mu m_{\rm u}}\ln(T^{3/2}/\rho)+{4\over 3}{aT^3\over\rho} +{\rm const}$

(1.18)

i vse proizvodnye vychislyayutsya analiticheski:

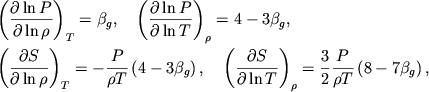$%\begin{displaymath} %\hbox{% %\begin{tabular}{ll} %$\displaystyle{ \left( \frac{\partial \ln P}{\partial \ln \rho }\right) _{T}=\beta _{g}, }$ & %$\displaystyle{ \left( \frac{\partial \ln P}{\partial \ln T}\right) _{\rho }=4-3\beta _{g}, }$ \\ %$\displaystyle{ \left( \frac{\partial S}{\partial \ln \rho }\right) _{T}=-\frac{P}{\rho T}\left( 4-3\beta _{g}\right), }$ & %$\displaystyle{ \left( \frac{\partial S}{\partial \ln T}\right) _{\rho }=\frac{3}{2}\frac{P}{\rho T}\left( 8-7\beta _{g}\right). }$ \\ %\end{tabular}} %\end{displaymath} \eqalign{ %(1.19) &\left(\partial \ln P\over \partial\ln\rho\right)_T=\beta_g, \quad \left(\partial \ln P\over \partial\ln T\right)_\rho=4-3 \beta_g, \cr &\left(\partial S\over \partial\ln \rho\right)_T=-{P\over\rho T} \left(4-3 \beta_g\right), \quad \left(\partial S\over \partial\ln T\right)_\rho= {3\over 2}{P\over\rho T}\left(8-7 \beta_g\right), \cr}$

(1.19)

Zdes' $\beta _{g}=P_{g}/P$ - otnoshenie gazovogo davleniya k polnomu. Vyrazheniya dlya adiabaticheskih pokazatelei i teploemkostei odnoatomnogo gaza s $\mu =const$ i izlucheniya prinimayut vid [218]

$\eqalign{ &\gamma_1=\beta_g +{2\over 3}{\left(4-3 \beta_g\right)^2\over 8-7 \beta_g}, \quad \gamma_2=\left[4-3\beta_g+{3\over 2}\beta_g{8-7\beta_g\over 4-3\beta_g} \right]^{-1},\cr &\gamma_3={2\over 3}{4-3 \beta_g\over 8-7 \beta_g}, \cr &c_v={3\over 2}{P\over\rho T}\left(8-7 \beta_g\right), \cr &c_p={3\over 2}{P\over\rho T}\left(8-7 \beta_g\right) \left[1+{2\over 3}{\left(4-3 \beta_g\right)^2\over\beta_g \left(8-7 \beta_g\right)}\right], \cr &{c_p\over c_v}=1+{2\over 3}{\left(4-3 \beta_g\right)^2\over\beta_g \left(8-7 \beta_g\right)}=\gamma_1/\beta_g. \cr}$

(1.20)

Sootnosheniya (1.18)-(1.20) shiroko primenyayutsya pri opisanii zvezd noi materii, tak kak osnovnaya chast' massy zvezd nahoditsya v sostoyanii polnoi ionizacii s $\mu =const$ . V obolochkah zvezd, gde temperatura men'she, veshestvo ionizovano ne polnost'yu i $\mu =\mu \left( \rho ,T\right)$ .

Zadacha. Vyvesti uravneniya dlya koncentracii elektronov v plazme, sostoyashei iz $H^{0},$ $H^{+},$ $H^{-}$ , $He^{0},$ $He^{+},$ $He^{++}$ , a takzhe atomov i odnokratno ionizovannyh ionov $k$ drugih elementov.

Reshenie. Ispol'zuya formulu Saha (1.8) i tabl. 2, poluchaem dlya vodoroda

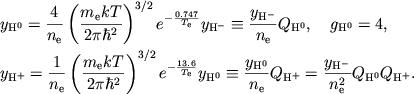$\eqalign{ &y_{\rm H^0}={4\over n_{\rm e}}\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{0.747 \over T_{\rm e}}} y_{\rm H^-}\equiv {y_{\rm H^-} \over n_{\rm e}}Q_{\rm H^0}, \quad g_{\rm H^0}=4, \cr &y_{\rm H^+}={1\over n_{\rm e}}\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{13.6 \over T_{\rm e}}} y_{\rm H^0}\equiv {y_{\rm H^0} \over n_{\rm e}}Q_{\rm H^+}= {y_{\rm H^-} \over n_{\rm e}^2}Q_{\rm H^0}Q_{\rm H^+}. \cr}$

(1)

$\begin{displaymath}y_{H^{+}}=\frac{1}{n_{e}}\left( \frac{m_{e}kT}{2\pi h^{2}}\right) ^{3/2}e^{-\frac{13.6}{T_{\mbox{e}}}}y_{H^{0}}\equiv \frac{y_{H^{0}}}{n_{e}}Q_{H^{+}}=\frac{y_{H^{-}}}{n_{e}^{2}}Q_{H^{0}}Q_{H^{+.}} \end{displaymath}$

Ispol'zuya uslovie $%$ y_{H^{-}}+y_{H^{0}}+y_{H^{+}}=1 $ y_{\rm H^-}+y_{\rm H^0}+y_{\rm H^+}=1$ , imeem

$%\begin{displaymath}y_{H^{-}}=n_{e}^{2}\left( n_{e}^{2}+n_{e}Q_{H^{0}}+Q_{H^{0}}Q_{H^{+}}\right) ^{-1} \end{displaymath} y_{\rm H^-}=n_{\rm e}^2\left(n_{\rm e}^2+n_{\rm e}Q_{\rm H^0}+ Q_{\rm H^0}Q_{\rm H^+}\right)^{-1}$

(2)

Analogichno dlya geliya poluchaem

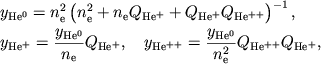$\eqalign{ &y_{\rm He^0}=n_{\rm e}^2\left(n_{\rm e}^2+n_{\rm e}Q_{\rm He^+}+ Q_{\rm He^+}Q_{\rm He^{++}}\right)^{-1}, \cr &y_{\rm He^+}={y_{\rm He^0} \over n_{\rm e}}Q_{\rm He^+}, \quad y_{\rm He^{++}}={y_{\rm He^0} \over n_{\rm e}^2} Q_{\rm He^{++}}Q_{\rm He^+}, \cr}$

(3)

gde

$%\begin{displaymath} %Q_{He^{+}}=4\left( \frac{m_{e}kT}{2\pi h^{2}}\right) ^{3/2}e^{-\frac{24.6}{T_{\mbox{e}}}}, \quad %Q_{He^{++}}=\left( \frac{m_{e}kT}{2\pi h^{2}}\right) ^{3/2}e^{-\frac{54.4}{T_{\mbox{e}}}} %\end{displaymath} Q_{\rm He^+}=4\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{24.6 \over T_{\rm e}}}, \quad Q_{\rm He^{++}}=\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{54.4 \over T_{\rm e}}}$

(4)

i dlya tyazhelyh elementov

$%\begin{displaymath} %y_{j^{+}}=\frac{Q_{j^{+}}}{n_{e}+Q_{j^{+}}} , \quad %Q_{j^{+}}=2\frac{g_{j^{+}}}{q_{j^{0}}}\left( \frac{m_{e}kT}{2\pi \hbar ^{2}}\right) ^{3/2}e^{-\frac{I_{j1}}{kT}} . %\end{displaymath} y_{j^+}={Q_{j^+}\over n_{\rm e}+ Q_{j^+}}, \quad Q_{j^+}=2{g_{j^+} \over g_{j^0}}\left(m_{\rm e}kT \over 2\pi\hbar^2 \right)^{3/2}e^{-{I_{j1} \over kT}}.$

(5)

Zdes' $T_{\mbox{e}}$ temperatura v elektronvol'tah. Ispol'zuya sootnoshenie (4) dlya kazhdogo elementa i uslovie elektroneitral'nosti (5)

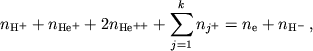
$%$ n_{H^{+}}+n_{He^{+}}+2n_{He^{++}}+\sum _{j=1}^{k}n_{j^{+}}=n_{e}+n_{H^{-}} $ n_{\rm H^+}+n_{\rm He^+}+2n_{\rm He^{++}}+\sum_{j=1}^kn_{j^+}= n_{\rm e}+n_{\rm H^-}\,,$

poluchaem uravnenie dlya privedennoi elektronnoi koncentracii

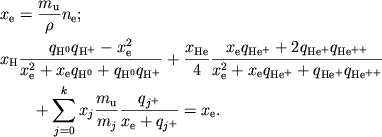$%\begin{displaymath} %\hbox{ %\begin{tabular}{l} %$\displaystyle{ x_{e}=\frac{m_{u}}{\rho }n_{e} , }$ %$\displaystyle{ x_{H}\frac{q_{_{^{H^{0}}}}q_{_{^{H^{+}}}}-x_{e}^{2}}{x^{2}_{e}+x_{e}q_{_{^{H^{0}}}}+q_{_{^{H^{0}}}}q_{_{^{j^{+}}}}}+\frac{x_{He}}{4}\frac{x_{e}q_{_{^{He^{+}}}}+2q_{_{^{He^{+}}}}q_{_{^{He^{++}}}}}{x_{e}^{2}+x_{e}q_{_{^{He^{+}}}}+q_{_{^{He^{+}}}}q_{_{^{He^{++}}}}}+ }$ %$\displaystyle{ \qquad\qquad + \Sigma _{j=0}^{k}\frac{m_{u}}{m_{j}}\frac{q_{_{^{j^{+}}}}}{x_{e}+q_{_{^{j^{+}}}}}=x_{e} . }$ %\end{tabular}} %\end{displaymath} \eqalign{ &x_{\rm e}= {m_{\rm u}\over \rho} n_{\rm e}; \cr &x_{\rm H}{q_{\rm H^0}q_{\rm H^+}-x_{\rm e}^2 \over x_{\rm e}^2+x_{\rm e}q_{\rm H^0}+q_{\rm H^0}q_{\rm H^+}}+ {x_{\rm He} \over 4} {x_{\rm e}q_{\rm He^+}+2q_{\rm He^+}q_{\rm He^{++}} \over x_{\rm e}^2+x_{\rm e}q_{\rm He^+}+q_{\rm He^+}q_{\rm He^{++}}} \cr &\qquad+\sum_{j=0}^k x_j{m_{\rm u} \over m_j} {q_{j^+} \over x_{\rm e}+q_{j^+}} = x_{\rm e}. \cr}$

(6)

Zdes' $q_{i}=m_{u}Q_{i}/\rho$ . Vse velichiny v (6) bezrazmerny i blizki k edinice, chto udobno dlya chislennogo resheniya.

Posle nahozhdeniya stepenei ionizacii v zavisimosti ot $\rho$ i $T$ , mozhno vychislit' termodinamicheskie funkcii i ih proizvodnye. Na ris. 1 v kachestve primera takogo rascheta privedena zavisimost' $\gamma _{3}(\rho ,T)$ dlya smesi s sostavom $x_{H}=0.75$ , $x_{He}=0.22$ h i solnechnym sootnosheniem mezhdu drugimi elementami (tabl. 1). Dva minimuma na krivyh $\gamma _{3}\left\vert _{\rho }(T)\right.$ sootvetstvuyut oblastyam ionizacii vodoroda i pervoi ionizacii geliya. Pri maloi plotnosti $\rho =10^{-12}\mbox{~g}\cdot \mbox{sm}^{-3}$ vtoroi minimum popadaet v oblast' preobladaniya davleniya izlucheniya i potomu ne zameten.

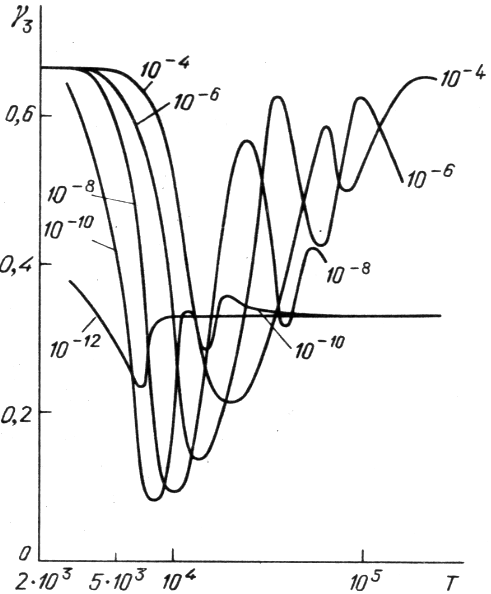Ris. 1. Zavisimosti $\gamma(T)$ pri $\rho$ = const, ukazannyh na krivyh, dlya normal'nogo sostava (tabl. 1) v oblasti, gde proishodit ionizaciya vodoroda i geliya

<< Predislovie | Oglavlenie | 2. Relyativistskii gaz s vyrozhdeniem >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce