Astronet > Fizicheskie voprosy teorii zvezdnoi evolyucii

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 2. Relyativistskii gaz s ... | Oglavlenie | 4. Veshestvo pri bol'shih ... >>

3. Uravnenie sostoyaniya pri nalichii yadernogo ravnovesiya i processov slabogo vzaimodeistviya

Kogda temperatura veshestva dostigaet neskol'kih milliardov kel'vinov, harakternye vremena yadernyh reakcii $t_{n}$ stanovyatsya men'she vseh makroskopicheskih vremen i ustanavlivaetsya ravnovesie otnositel'no yadernogo sostava. V usloviyah yadernogo ravnovesiya koncentracii yader nahodyatsya iz sootnosheniya mezhdu himicheskimi potencialami yader $\mu _{A,Z}$ , neitronov $\mu _{n}$ i protonov $\mu _{p}$ , analogichno usloviyu himicheskogo ravnovesiya

$\mu_{A,Z}=Z\mu_{\mathrm{n}}+(A-Z)\mu_{\mathrm{n}}.$

(3.1)

Dlya nerelyativistskih i nevyrozhdennyh yader imeem [145]

$\mu_{A,Z}=-kT\ln\left[\left(\AZ{m}kT\over 2\pi\hbar^2\right)^{3/2} {\AZ{g}\over \AZ{n}}\right]\AZ{m}c^2.$

(3.2)

Ravnovesnaya koncentraciya yader iz (3.1), (3.2) imeet vid

$\eqalign{ \AZ{n}&=\left(\pih\over kT\right)^{{3\over 2}(A-1)} \left(\AZ{m}\over {m_{\mathrm{p}}}^Z {m_{\mathrm{n}}}^{A-Z}\right)^{3/2} {\AZ{g}\over {g_{\mathrm{p}}}^Z {g_{\mathrm{n}}}^{A-Z}} \cr \noalign{\medskip} &\qquad\times\exp\left\{{[Zm_{\mathrm{p}}+(A-Z)m_{\mathrm{n}}-\AZ m]c^2\over kT}\right\} {n_{\mathrm{p}}}^Z {n_{\mathrm{n}}}^{A-Z}. \cr }$

(3.3)

V predeksponente dostatochno polozhit' $m_{n}=m_{p}=m_{u}$ , $m_{A,Z}=Am_{u}$ , a chislitel' v eksponente est' energiya svyazi yadra $B_{A,Z}$ . Uchtya takzhe $g_{p}=g_{n}=2$ , poluchim

$\AZ n=\left(\pih\over m_{\mathrm{p}} kT\right)^{{3\over 2}(A-1)} {A^{3/2}\over 2^A}\AZ g e^{{\AZ B\over kT}} {n_{\mathrm{p}}}^Z {n_{\mathrm{n}}}^{A-Z}.$

V tabl. 5 privedeny spiny $I$ , energii svyazi $B$ naibolee ustoichivyh yader, $g_{A,Z}=2I_{A,Z}+1$ . Blagodarya eksponencial'no bystroi zavisimosti skorosti yadernyh reakcii ot temperatury (sm. gl. 4), perehod ot zastyvshego yadernogo sostava k yadernomu ravnovesiyu zanimaet uzkuyu zonu temperatur, gde harakternye vremena yadernyh reakcii sravnimy s makroskopicheskimi (teplovym ili gidrodinamicheskim) i gde neobhodimo rassmotrenie kinetiki yadernyh reakcii. Pri dannoi temperature $T$ i plotnosti

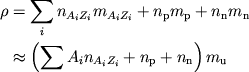$\eqalign{ \rho&=\sum_i n_{A_i Z_i}m_{A_i Z_i}+n_{\mathrm{p}} m_{\mathrm{p}}+n_{\mathrm{n}} m_{\mathrm{n}} \cr &\approx \left(\sum A_i n_{A_i Z_i}+n_{\mathrm{p}}+n_{\mathrm{n}}\right)m_{\mathrm{u}} \cr }$

(3.4)

dlya nahozhdeniya yadernogo sostava neobhodimo znat' svyaz' mezhdu koncentraciyami $n_{n}$ i $n_{p}$ .

Tablica 5. Energii svyazi i spiny yader stabil'nyh izotopov naibolee obil'nyh elementov [135, 180]

Atomnyi nomer	Element (izotop)	Energiya svyazi $E_{b}$ , keV	Spin yadra I
1	$^{1}H$ , $^{2}H$	0.2225	1/2, 1
2	$^{3}He$ , $^{4}He$	7718, 28297	1/2, 0
6	$^{12}C$ , $^{13}C$	92165, 97112	0, 1/2
7	$^{14}N$ , $^{15}N$	104663, 115496	1, 1/2
8	$^{16}O$ , $^{17}O$ , $^{18}O$	127624, 131766, 139813	0, 5/2, 0
10	$^{20}Ne$ , $^{21}Ne$ , $^{22}Ne$	160651, 167412, 177778	0, 3/2, 0
11	$^{23}Na$	186570	3/2
12	$^{24}Mg$ , $^{25}Mg$ , $^{26}Mg$	198262, 205594, 216688	0, 5/2, 0
13	$^{27}Al$	224959	5/2
14	$^{28}Si$ , $^{29}Si$ , $^{30}Si$	236544, 245018, 255627	0, 1/2, 0
15	$^{31}P$	262925	1/2
16	$^{32}S$ , $^{33}S$ , $^{34}S$	271789, 280432, 291847	0, 3/2, 0
17	$^{35}Cl$ , $^{37}Cl$	298220, 317112	3/2, 3/2
18	$^{36}Ar$ , $^{38}Ar$ , $^{40}Ar$	306727, 327354, 343822	0, 0, 0
20	$^{40}Ca$ , $^{42}Ca$ , $^{43}Ca$	342063, 361900, 369832	0, 0, 7/2
	$^{44}Ca$ , $^{46}Ca$ , $^{48}Ca$	380969, 398787, 416014	0, 0, 0
24	$^{50}Cr$ , $^{52}Cr$ , $^{53}Cr$ , $^{54}Cr$	435061, 456364, 464304, 474024	0, 0, 3/2, 0
25	$^{55}Mn$	482091	5/2
26	$^{54}Fe$ , $^{56}Fe$ , $^{57}Fe$ , $^{58}Fe$	471779, 492280, 499926, 509969	0, 0, 1/2, 0
28	$^{58}Ni$ , $^{60}Ni$ , $^{61}Ni$	506484, 526871, 534691	0, 0, 3/2
	$^{62}Ni$ , $^{64}Ni$	545288, 561788	0, 0
$B_{A,Z}=\left( Zm_{p}+\left( A-Z\right) m_{n}-m_{A,Z}\right) c^{2}$
$m_{n}=m_{p}+m_{e}+782.5$ keV

Vzaimoprevrasheniya protonov i neitronov, kak svobodnyh, tak i svyazannyh v yadrah, proishodyat v reakciyah slabogo vzaimodeistviya (sm. gl. 5). Harakternoe vremya slabyh processov $t_{\beta }$ pri vysokoi temperature znachitel'no bol'she yadernogo $t_{n}$ i mozhet byt' poryadka mikroskopicheskogo, gidrodinamicheskogo ili teplovogo. Neitrino, voznikayushie pri slabyh vzaimodeistviyah, svobodno uletayut iz zvezd. V etih usloviyah termodinamicheskoe ravnovesie otnositel'no reakcii slabogo vzaimodeistviya otsutstvuet. Isklyuchenie sostavlyayut goryachie neitronnye zvezdy, kotorye neproznachny dlya neitrino s energiei $E_{\nu _{e}}\geq 1\mbox{~MeV}$ . Termodinamicheskie funkcii ravnovesnogo neitrinnogo gaza $\nu _{e}$ , $\widetilde{\nu _{e}}$ -gaza s $kT\gg m_{\mu _{e}}c^{2}$ ⁵ analogichny elektronnym (2.56), gde $\beta =\mu _{\nu _{e}}/kT$ , a velichiny $E_{\nu _{e}\widetilde{\nu _{e}}}$ , $P_{\nu _{e}\widetilde{\nu _{e}}}$ , $S_{\nu _{e}\widetilde{\nu _{e}}}$ v dva raza men'she, chem $E_{e\pm }$ , $P_{e\pm }$ i $S_{e\pm }$ za schet statisticheskogo vesa. V levoi chasti pervogo sootnosheniya (2.56), sluzhashego dlya nahozhdeniya $\mu _{\nu _{e}}$ , $\rho /\mu _{Z}m_{u}$ vmesto $\rho /\mu _{Z}m_{u}$ dolzhna stoyat' velichina, svyazannaya s koncentraciei leptonnogo zaryada $Q_{\nu _{e}}:2\left( Q_{\nu _{e}}-n_{e-}+n_{e+}\right) =2\left( n_{\nu _{e}}-n_{\widetilde{\nu _{e}}}\right)$ . Posle takih zamen vse formuly p.d 2 primenimy dlya ravnovesnogo neitrinnogo gaza, a svyaz' mezhdu $n_{p}$ i $n_{n}$ opredelyaetsya sootnosheniyami mezhdu himicheskimi potencialami

$\mu_{\mathrm{n}}=\mu_{\mathrm{p}}+\mute+\mu_{\nuet},\quad \mu_{\nuet}=-\mu_{\nue}.$

(3.5)

Vtoroe sootnoshenie (3.5) sleduet iz ravnovesiya reakcii $\nu _{e}+\widetilde{\nu _{e}}\rightarrow e^{+}+e^{-}$ i usloviya (2.11). Ravnovesie drugih tipov neitrino $\nu _{\mu }$ i $\nu _{\tau }$ opisyvaetsya analogichno $\nu _{e}$ , hotya ono vryad li dostizhimo dazhe v goryachih neitronnyh zvezdah iz-za bol'shoi massy ih leptonov.

V usloviyah svobodnogo uleta neitrino strogoe nahozhdenie svyazi $n_{p}$ i $n_{n}$ sostoit v reshenii uravnenii kinetiki beta-processov

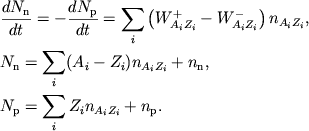$\eqalign{ &{dN_{\mathrm{n}}\over dt}=-{dN_{\mathrm{p}}\over dt} =\sum_i\left(W_{A_iZ_i}^+ -W_{A_iZ_i}^-\right)n_{A_iZ_i}, \cr &N_{\mathrm{n}}=\sum_i(A_i-Z_i)n_{A_i Z_i}+n_{\mathrm{n}}, \cr &N_{\mathrm{p}}=\sum_i Z_i n_{A_i Z_i}+n_{\mathrm{p}}. \cr }$

(3.6)

pri izvestnom nachal'nom sootnoshenii mezhdu $N_{n}$ i $N_{p}$ . V rabote [328] parametr $N_{n}/N_{p}$ schitalsya nezavisimym pri raschetah yadernogo ravnovesiya elementov gruppy zheleza. V pervom sootnoshenii (3.6) pri summirovanii nuzhno uchityvat' svobodnye neitrony i protony. Skorosti beta-reakcii ( $c^{-1}$ ) $W^{+}_{A,Z}=W_{A,Z}(e^{+}-\mbox{raspad})+W_{A,Z}(e^{-}-\mbox{zahvat})$ i $W^{-}_{A,Z}=W_{A,Z}(e^{-}-\mbox{raspad})+W_{A,Z}(e^{+}-\mbox{zahvat})$ rassmotreny v paragrafe 19.

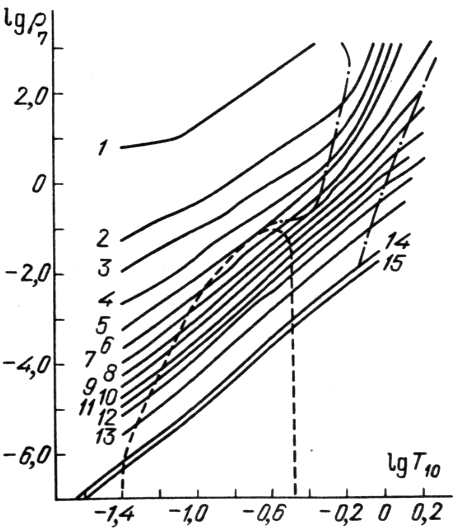Ris. 6. Izentropy veshestva na ploskosti $T$ , $\rho$ . Dlya 10⁹ < T < 2^.10¹⁰K, 10⁵ < $\rho$ < 10¹⁰ g/sm³ izentropy postroeny dlya ravnovesnogo himicheskogo sostava po dannym raboty [114]. Shtrihovaya liniya razdelyaet oblasti $\gamma_1$ > 4/3 i $\gamma_1$ < 4/3 i postroena po dannym raschetov [46]. Shtrihpunktirnye linii razdelyayut oblasti $\gamma_1$ > 4/3 i $\gamma_1$ < 4/3 i postroeny po dannym raboty [114] s uchetom raspada zheleza. Cifry na risunke sootvetstvuyut sleduyushim ieentropam: 1 - $S_{10}$ = 0,003981, 2 - $S_{10}$ = 0,01, 3 - $S_{10}$ = 0,01585, 4 - $S_{10}$ = 0,02512, 5 - $S_{10}$ = 0,03981, 6 - $S_{10}$ = 0,0631, 7 - $S_{10}$ = 0,1, 8 - $S_{10}$ = 0,1585, 9 - $S_{10}$ = 0,2512, 10 - $S_{10}$ = 0,3981, 11 - $S_{10}$ = 0,631, 12 - $S_{10}$ = 1,0, 13 - $S_{10}$ = 2,512, 14 - $S_{10}$ = 10, 15 - $S_{10}$ = 15,85, $S_{10} = S/10$ erg g^-1 K^-1

Esli v techenie vremeni $t\gg t_{\beta }$ velichiny $T$ i $\rho$ v zvezde menyayutsya slabo, to dostigaetsya kineticheskoe ravnovesie po beta-processam s $dN_{n}/dt=0$ v (3.6). V etom sluchae sootnosheniya (3.6) odnoznachno opredelyayut sostav veshestva [117-119, 224]. Dlya priblizhennogo opredeleniya sostava v usloviyah svobodnogo uleta neitrino inogda ispol'zuetsya sootnoshenie (3.5) s $\mu _{\nu _{e}}=0$ . Raschety v etom priblizhenii sdelany v [114]. V yadernom ravnovesii uchityvalis' yadra zheleza $^{56}Fe$ , vklyuchaya sem' pervyh vozbuzhdennyh urovnei, $^{4}He$ , $n$ i $p$ . Rost temperatury vedet snachala k rasshepleniyu yader zheleza na $^{4}He$ i nuklony, a zatem k chisto nuklonnomu sostavu. Pri bol'shoi plotnosti osnovnuyu chast' svobodnyh nuklonov sostavlyayut neitrony. Na ris. 6 iz [46] privedeny izentropy veshestva na ploskosti $\rho$ , $T$ i ukazany oblasti s $\gamma _{1}\lt 4/3$ , neobhodimye dlya analiza ustoichivosti (sm. gl.12). V oblasti yadernogo ravnovesiya ispol'zovalis' rezul'taty [114].

<< 2. Relyativistskii gaz s ... | Oglavlenie | 4. Veshestvo pri bol'shih ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce