Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu << 3. Uravnenie sostoyaniya pri ... | Oglavlenie |

4. Veshestvo pri ochen' bol'shih plotnostyah, neitronizaciya, vzaimodeistvie chastic

Pri ochen' bol'shih plotnostyah v usloviyah sil'noyu vyrozhdeniya elektronov i nuklonov priblizhenno veshestvo mozhno schitat' holodnym s \( T=S=0 \) [110].

a) Holodnaya neitronizaciya vdol' sostoyanii minimuma energii (SME).

Pri plotnostyah \( \rho \lt 8.1\mbox{~g}\cdot \mbox{sm}^{-3} \) veshestvo v SME sostoit iz \( ^{56}Fe \), yadra kotorogo maksimal'no stabil'ny6. Kogda \( \epsilon _{Fe} \) iz (2.21) dostigaet znacheniya \( \epsilon _{\beta } \) pri

$$ %\begin{displaymath} %\epsilon _{\beta }\left( A,Z\right) =\left( m_{A,Z-1}-m_{A,Z}\right) c^{2}-m_{e}c^{2}=B_{A,Z}-B_{A,Z-1}+\left( m_{n}-m_{p}\right) c^{2}-m_{e}c^{2} , %\end{displaymath} \eqalign{ \epsilon_\beta(A,Z)&=(m_{A,Z-1}-\AZ m)c^2-\mec{}2 \cr &=\AZ B-B_{A,Z-1}+(m_{\mathrm{n}}-m_{\mathrm{p}})c^2-\mec{}2, \cr } $$ (4.1)

zahvat elektrona stabil'nym yadrom \( \left( A,Z\right) \) stanovitsya energeticheski vygodnym. Yadro \( \left( A,Z-1\right) \), kotoroe v obychnyh usloviyah yavlyaetsya \( \beta ^{-} \) radioaktivnym, pri bol'shoi energii Fermi elektronov okazyvaetsya ustoichivym. Process zahvata elektrona yadrom, nazyvaemyi neitronizaciei, rasschitan vpervye v [216].

Pri nulevoi temperature sostoyanie termodinamicheskogo ravnovesiya sootvetstvuet minimumu polnoi energii \( E_{tot} \) kak funkcii \( A \) i \( Z \) pri dannom chisle nuklonov v edinice ob'ema. S rostom plotnosti ravnovesie smeshaetsya v storonu vse bolee pereobogashennyh neitronami yader. Pri \( \rho \geq \rho _{nd} \) energiya svyazi poslednego neitrona v yadre \( Q_{n} \) blizka k nulyu i v ravnovesii poyavlyayutsya svobodnye neitrony. V ravnovesii plotnost', pri kotoroi nachinayut otsheplyat'sya neitrony, ravna \( \rho _{nd}=4.3\cdot 10^{11}\mbox{~g}\cdot \mbox{sm}^{-3} \) [267].

V otsutstvie svobodnyh neitronov pri \( \rho \lt \rho _{nd} \) dlya energii edinicy ob'ema s uchetom energii pokoya imeem [267]

\begin{displaymath} \hbox{% \begin{tabular}{l} $\displaystyle{ E_{tot}\left( A,Z,n_{b}\right) =n_{A,Z}\left( m_{A,Z}c^{2}+W_{L}\right) +E_{e}\left( n_{e}\right) , }$ $\displaystyle{ n_{e}=Zn_{A,Z} , \quad n_{b}=An_{A,Z} . }$ \end{tabular}} \end{displaymath} (4.2)

Massy stabil'nyh yader opredelyayutsya s uchetom energii svyazi iz tabl. 4. Dlya yader, dalekih ot oblasti stabil'nosti, eksperimental'nye izmereniya massy \( m_{A,Z} \) otsutstvuyut. V etom sluchae ispol'zuyutsya poluempiricheskie (teoreticheskie, podpravlennye imeyushimisya eksperimental'nymi dannymi) formuly. Naibolee prostaya, otrazhayushaya vse kachestvennye zakonomernosti formula dlya energii svyazi, poluchennaya Veiczekkerom, imeet vid [23]
\begin{displaymath} B_{A,Z}=15.568-17.226A^{2/3}-0.698\frac{Z^{2}}{A^{1/3}}-23.279\frac{\left( A-2Z\right) ^{2}}{A}+\frac{34}{A^{3/4}}\delta \mbox{~MeV} \end{displaymath} (4.3)

Zdes' \( \delta =1 \) dlya chetnyh \( A \) i \( Z \), \( \delta =0 \) dlya nechetnyh \( A \) i lyubyh \( Z \), \( \delta =-1 \) dlya chetnyh \( A \) i nechetnyh \( Z \). V (4.3) uchteny statisticheskie i kapel'nye svoistva yader, energiya yadernogo vzaimodeistviya s uchetom effektov nesimmetrii (\( A\neq 2Z \)) i sparivaniya nuklonov, kulonovskaya i poverhnostnaya energii yader. Raschet ravnovesnogo sostava pri holodnoi neitronizacii s ispol'zovaniem formuly Veiczekkera sdelan v [77]. V rabote [267] dlya analogichnyh raschetov ispol'zovana bolee tochnaya, no gorazdo bolee slozhnaya formula Maiersa i Svyateckogo [486]. Energiya holodnyh elektronov dana v (2.22), (2.23), a velichina \( W_{L} \) est' energiya elektrostaticheskogo vzaimodeistviya, voznikayushaya iz-za nalichiya tochechnyh polozhitel'nyh zaryadov v odnorodnom fone otricatel'nyh. Minimum \( W_{L} \) dostigaetsya dlya ob'emno-centrirovannoi kubicheskoi reshetki i opredelyaetsya formuloi [267]
\begin{displaymath} W_{L}=-1.819620Z^{2}e^{2}/b , \quad n_{A,Z}b^{3}=2 . \end{displaymath} (4.4)

Elektrostaticheskoe vzaimodeistvie umen'shaet energiyu i davlenie veshestva, tak kak rasstoyanie mezhdu ottalkivayushimisya yadrami v srednem bol'she, chem mezhdu prityagivayushimisya zaryadami raznogo znaka [110]. Ravnovesnyi sostav, sootvetstvuyushii minimumu \( E_{tot} \) iz (4.2) pri zadannoi plotnosti barionov \( n_{b} \) priveden v tabl. 6 iz raboty [267]. Otmetim, chto mezhdu plotnostyami \( \rho _{max} \) i \( \rho _{max}\left( 1+\frac{\Delta \rho }{\rho }\right) \) davlenie pochti postoyanno (slabo rastet za schet davleniya yader). Velichina \( \rho =E_{tot}/c^{2} \) uchityvaet kineticheskuyu energiyu i energiyu vzaimodeistviya. Davlenie \( P \) k relyativistskii pokazatel' adiabaty \( \Gamma \) opredelyayutsya formulami [267]
\begin{displaymath} P=\left. n_{b}^{2}\frac{\partial \left( E_{tot}/n_{b}\right) }{\partial n_{b}}\right\vert _{S} , \quad \Gamma=\left. \frac{n_{b}}{P}\frac{\partial P}{\partial n_{b}}\right\vert _{S}=\frac{\rho +P/c^{2}}{P}\left( \frac{\partial P}{\partial \rho }\right) _{S} . \end{displaymath} (4.5)


Tablica 6. Ravnovesnyi yadernyi sostav pri plotnostyah, men'shih plotnosti ispareniya neitronov (iz [267])
Yadro \( B_{n},\mbox{~MeV} \) Z/A \( \rho _{max},\mbox{~g}\cdot \mbox{sm}^{-3} \) \( \mu _{te},\mbox{~MeV} \) \( \Delta \rho /\rho ,\% \)
\( ^{56}Fe \) 8.7905 0.4643 8.1 (6) 0.95 2.9
\( ^{62}Ni \) 8.7947 0.4516 2.7 (8) 2.6 3.1
\( ^{64}Ni \) 8.7777 0.4375 1.2 (9) 4.2 7.9
\( ^{84}Se \) 8.6797 0.4048 8.2 (9) 7.7 3.5
\( ^{82}Ge \) 8.5964 0.3902 2.2 (10) 10.6 3.8
\( ^{80}Zn \) 8.4675 0.3750 4.8 (10) 13.6 4.1
\( ^{78}Ni \) 8.2873 0.3590 1.6 (11) 20.0 4.6
\( ^{76}Fe \) 7.9967 0.3421 1.8 (11) 20.2 2.2
\( ^{124}Mo \) 7.8577 0.3387 1.9 (11) 20.5 3.1
\( ^{122}Zr \) 7.6705 0.3279 2.7 (11) 22.9 3.3
\( ^{120}Sr \) 7.4522 0.3166 3.7 (11) 25.2 3.5
\( ^{118}Kr \) 7.2002 0.3051 (4.3 (11)) (26.2) ...
Zdes' \( B_{n}=B_{A,Z}/A \) - energiya svyazi na nuklon, \( \rho _{max} \) - maksimal'naya plotnost', pri kotoroi sushestvuet dannyi nuklid, \( \mu _{te} \) - himicheskii potencial elektronov pri etoi plotnosti, \( \Delta \rho /\rho \) - otnositel'noe uvelichenie plotnosti pri perehode k sleduyushemu nuklidu. Pri \( \rho _{max}=4.3\cdot 10^{11}\mbox{~g}\cdot \mbox{sm}^{-3} \) - nachinaetsya isparenie neitronov.

V tablice 7 dany rezul'taty rascheta termodinamicheskih funkcii pri ravnovesnoi neitronizacii. Pri \( \rho \lt 10^{4}\mbox{~g}\cdot \mbox{sm}^{-3} \), kogda energiya vzaimodeistciya \( W_{L} \) stanovitsya poryadka kineticheskoi energii elektronov, znacheniya v tabl. 7 vzyaty iz raboty [201].


Tablica 7. Uravnenie sostoyaniya veshestva v ravnovesii, sootetstvuyushem minimumu polnoi energii, iz [267]
\( \rho ,\mbox{~g}\cdot \mbox{~sm}^{-3} \) \( P,\mbox{~din}\cdot \mbox{sm}^{-2} \) \( n_{b},\mbox{~sm}^{-3} \) Z A G
7.86 \( \geq \)1.01 (9) 4.73 (24) 26 56 ...
7.90 1.01 (10) 4.76 (24) 26 56 ...
8.15 1.01 (11) 4.91 (24) 26 56 ...
11.6 1.21 (12) 6.99 (24) 26 56 ...
16.4 1.40 (13) 9.90 (24) 26 56 ...
45.1 1.70 (14) 2.72 (25) 26 56 ...
212 5.82 (15) 1.27 (26) 26 56 ...
1150 1.90 (17) 6.93 (26) 26 56 ...
1.044 (4) 9.744 (18) 6.295 (27) 26 56 1.796
2.622 (4) 4.968 (19) 1.581 (28) 26 56 1.744
6.587 (4) 2.431 (20) 3.972 (28) 26 56 1.706
1.654 (5) 1.151 (21) 9.976 (28) 26 56 1.670
4.156 (5) 5.266 (21) 2.506 (29) 26 56 1.631
1.044 (6) 2.318 (22) 6.294 (29) 26 56 1.586
2.622 (6) 9.755 (22) 1.581 (30) 26 56 1.534
6.588 (6) 3.911 (23) 3.972 (30) 26 56 1.482
8.293 (6) 5.259 (23) 5.000 (30) 28 62 1.471
1.655 (7) 1.435 (24) 9.976 (30) 28 62 1.437
3.302 (7) 3.833 (24) 1.990 (31) 28 62 1.408
6.589 (7) 1.006 (25) 3.972 (31) 28 62 1.386
1.315 (8) 2.604 (25) 7.924 (31) 28 62 1.369
2.624 (8) 6.676 (25) 1.581 (32) 28 62 1.357
3.304 (8) 8.738 (25) 1.990 (32) 28 64 1.355
5.237 (8) 1.629 (26) 3.155 (32) 28 64 1.350
8.301 (8) 3.029 (26) 5.000 (32) 28 64 1.346
1.045 (9) 4.129 (26) 6.294 (32) 28 64 1.344
1.316 (9) 5.036 (26) 7.924 (32) 34 84 1.343
1.657 (9) 6.860 (26) 9.976 (32) 34 84 1.342
2.626 (9) 1.272 (27) 1.581 (33) 34 84 1.340
4.164 (9) 2.356 (27) 2.506 (33) 34 84 1.338
6.601 (9) 4.362 (27) 3.972 (33) 34 84 1.337
8.312 (9) 5.662 (27) 5.000 (33) 32 82 1.336
1.046 (10) 7.702 (27) 6.294 (33) 32 82 1.336
1.318 (10) 1.048 (28) 7.924 (33) 32 82 1.336
1.659 (10) 1.425 (28) 9.976 (33) 32 82 1.335
2.090 (10) 1.938 (28) 1.256 (34) 32 82 1.335
2.631 (10) 2.503 (28) 1.581 (34) 30 80 1.335
3.313 (10) 3.404 (28) 1.990 (34) 30 80 1.335
4.172 (10) 4.628 (28) 2.506 (34) 30 80 1.334
5.254 (10) 5.949 (28) 3.155 (34) 28 78 1.334
6.617 (10) 8.089 (28) 3.972 (34) 28 78 1.334
8.332 (10) 1.100 (29) 5.000 (34) 28 78 1.334
1.049 (11) 1.495 (29) 6.294 (34) 28 78 1.334
1.322 (11) 2.033 (29) 7.924 (34) 28 78 1.334
1.664 (11) 2.597 (29) 9.976 (34) 26 76 1.334
1.844 (11) 2.892 (29) 1.105 (35) 42 124 1.334
2.096 (11) 3.290 (29) 1.256 (35) 40 122 1.334
2.640 (11) 4.473 (29) 1.581 (35) 40 122 1.334
3.325 (11) 5.816 (29) 1.990 (35) 38 120 1.334
4.188 (11) 7.538 (29) 2.506 (35) 36 118 1.334
4.299 (11) 7.805 (29) 2.572 (35) 36 118 1.334

b) Poyavlenie svobodnyh nuklonov. SME pri sub'yadernyh plotnostyah s uchetom vzaimodeistviya nuklonov.

Pri \( \rho \gt \rho _{nd} \) vse svyazannye sostoyaniya neitronov v yadrah okazyvayutsya zapolnennymi i dal'neishii rost plotnosti privodit k poyavleniyu svobodnyh neitronov. Posle razlichnyh popytok rascheta uravneniya sostoyaniya v etoi oblasti (sm. obzor [266]), korrektnyi podhod k resheniyu problemy byl razvit v rabote [265]. Etot podhod osnovan na sleduyushih principah.

  1. Edinoe opisanie energii vzaimodeistviya nuklonov kak vnutri, tak i vne yader.

  2. Ispol'zovanie vyrazheniya dlya poverhnostnoi energii yader, kotoroe uchityvaet nalichie okruzhayushih neitronov i obrashaetsya v nul' pri identichnosti veshestva vnutri i snaruzhi.

  3. Uchet energii kulonovskogo vzaimodeistviya elektronov i yader reshetki, a takzhe protonov vnutri yadra.

Esli \( n_{A,Z} \) i \( n_{n} \) - koncentracii yader i svobodnyh neitronov v prostranstve vne yader, \( V_{A,Z} \) - ob'em yadra, a to vyrazhenie dlya polnoi energii edinicy ob'ema \( E_{tot} \) zapishetsya v vide


\begin{displaymath} E_{tot}\left( A,Z,n_{n},n_{A,Z},V_{A,Z}\right) =n_{A,Z}\left( W_{A,Z}+W_{L}\right) +\left( 1-V_{A,Z}n_{A,Z}\right) E_{n}\left( n_{n}\right) +E_{e}\left( n_{e}\right) . \end{displaymath} (4.6)

Dlya nahozhdeniya ravnovesnogo sostava i uravneniya sostoyaniya neobhodimo minimizirovat' \( E_{tot} \) otnositel'no argumentov pri postoyannoi koncentracii nuklonov \( n_{b} \):


\begin{displaymath} n_{b}=An_{A,Z}+\left( 1-V_{A,Z}n_{A,Z}\right) n_{n} . \end{displaymath} (4.7)

Vhodyashie v (4.6) kulonovskaya energiya reshetki \( W_{L} \) i energiya holodnyh elektronov opredeleny v (4.4) i (2.22), (2.23) sootvetstvenno. Energiya yadra, predstavlyaemogo v vide zhidkoi kapli, zapisyvaetsya v vide


\begin{displaymath} \eqalign{ W_{A,Z}\left( A,Z,V_{A,Z},n_{n}\right) =& \left[ \left( 1-x\right) m_{n}c^{2}+xm_{p}c^{2}+W\left( k,x\right) \right] A+ \cr & +W_{coul}\left( A,Z,V_{A,Z},n_{n}\right) +W_{surf}\left( A,Z,V_{A,Z},n_{n}\right), \quad x=\frac{Z}{A}, \cr } \end{displaymath} (4.8)

gde \( W\left( k,x\right) \) - energiya na odin barion v odnorodnoi yadernoi materii s koncentraciei \( n=k^{3}/1.5\pi ^{2}=A/V_{A,Z} \), \( W_{coul} \) - kulonovskaya energiya vzaimodeistviya protonov v yadre, \( W_{surf} \) - poverhnostnaya energiya yadra. Formula dlya energii neitronnogo gaza \( E_{n} \) poluchaetsya analogichno (4.8) pri \( x=0 \)


\begin{displaymath} E_{n}\left( n_{n}\right) =n_{n}W\left( k_{n},0\right) +m_{n}c^{2} , \quad n_{n}=k_{n}^{3}/1.5\pi ^{2} . \end{displaymath} (4.9)

Funkciya \( W\left( k,x\right) \), vhodyashaya v (4.8), (4.9), a takzhe \( W_{coul} \) i \( W_{surf} \), vhodyashie v (4.8), vychisleny v [266]. Poverhnostnaya energiya v [265] ocenivalas' dovol'no grubo iz soobrazhenii razmernosti. Bolee tochnye vyrazheniya dlya \( W_{surf} \) byli naideny v rabotah [313] metodom Tomasa-Fermi, [256] variacionnym metodom i [504, 548] metodom Hartri-Foka. Velichina - \( \left[ W\left( k,x\right) A+W_{coul}+W_{surf}\right] \) po fizicheskomu smyslu est' energiya svyazi yadra \( \left( A,Z\right) \) s uchetom okruzhayushei plotnosti neitronov, kotoraya dlya normal'nyh yader v vakuume approksimiruetsya formuloi Veiczekkera (4.3). Minimizaciya velichiny \( E_{tot} \) otnositel'no svoih argumentov pri postoyanstve \( n_{b} \) iz (4.7) svoditsya k chetyrem uravneniyam, opredelyayushim ravnovesie po sleduyushim processam: 1) szhatie i rasshirenie yadra davleniem vneshnih neitronov, 2) obmen neitronami mezhdu yadrom i neitronnym gazom, 3) prevrashenie neitronov i protonov drug v druga vnutri yadra, 4) vydelenie yadra, minimiziruyushego polnuyu energiyu. Reshenie etih chetyreh uravnenii opredelyaet svoistva ravnovesnogo veshestva, sostoyashego iz yader i svobodnyh neitronov. V tabl.8 iz [265] privedeny rezul'taty raschetov. S uvelicheniem plotnosti proishodit rost massy i ob'ema yader, poka oni ne kasayutsya drug druga pri \( \rho _{nm}=2.4\cdot 10^{14}\mbox{~g}\cdot \mbox{sm}^{-3} \). V [265] predpolagaetsya, chto pri plotnosti \( \rho _{nn} \) proishodit fazovyi perehod pervogo roda k odnorodnoi yadernoi materii.


Tablica 8. Harakteristiki veshestva v minimume polnoi energii pri nalichii svobodnyh neitronov (iz [265])
\( \rho ,\mbox{~g}\cdot \mbox{sm}^{-3} \) \( P,\mbox{~din}\cdot \mbox{sm}^{-3} \) \( n_{b},\mbox{~sm}^{-3} \) Z A G
4.460(11) 7.890(29) 2.,670(35) 40 126 0.40
5.228(11) 8.352(29) 3.126(35) 40 128 0.36
6.610(11) 9.098(29) 3.951(35) 40 130 0.40
7.964(11) 9.831(29) 4.759(35) 41 132 0.46
9.728(11) 1.083(30) 5.812(35) 41 135 0.54
1.196(12) 1.218(30) 7.143(35) 42 137 0.63
1.471(12) 1.399(30) 8.786(35) 42 140 0.73
1.805(12) 1.638(30) 1.077(36) 43 142 0.83
2.202(12) 1.950(30) 1.314(36) 43 146 0.93
2.930(12) 2.592(30) 1.748(36) 44 151 1.06
3.833(12) 3.506(30) 2.287(36) 45 156 1.17
4.933(12) 4.771(30) 2.942(36) 46 163 1.25
6.248(12) 6.481(30) 3.726(36) 48 170 1.31
7.801(12) 8.748(30) 4.650(36) 49 178 1.36
9.611(12) 1.170(31) 5.728(36) 50 186 1.39
1.246(13) 1.695(31) 7.424(36) 52 200 1.43
1.496(13) 2.209(31) 8.907(36) 54 211 1.44
1.778(13) 2.848(31) 1.059(37) 56 223 1.46
2.210(13) 3.931(31) 1.315(37) 58 241 1.47
2.988(13) 6.178(31) 1.777(37) 63 275 1.49
3.767(13) 8.774(31) 2.239(37) 67 311 1.51
5.081(13) 1.386(32) 3.017(37) 74 375 1.53
6.193(13) 1.882(32) 3.675(37) 79 435 1.54
7.732(13) 2.662(32) 4.585(37) 88 529 1.56
9.826(13) 3.897(32) 5.821(37) 100 683 1.60
1.262(14) 5.861(32) 7.468(37) 117 947 1.65
1.586 (14) 8.595 (32) 9.371 (37) 143 1390 1.70
2.004(14) 1.286(33) 1.182(38) 201 2500 1.74
2.520(14) 1.900(33) 1.484(38) ... ... 1.81
2.761(14) 2.242(33) 1.625(38) ... ... 1.82
3.085(14) 2.751(33) 1.814(38) ... ... 1.87
3.433(14) 3.369(33) 2.017(38) ... ... 1.92
3.885(14) 4.286(33) 2.280(38) ... ... 1.97
4.636(14) 6.103(33) 2.715(38) ... ... 2.03
5.094(14) 7.391(33) 2.979(38) ... ... 2.05

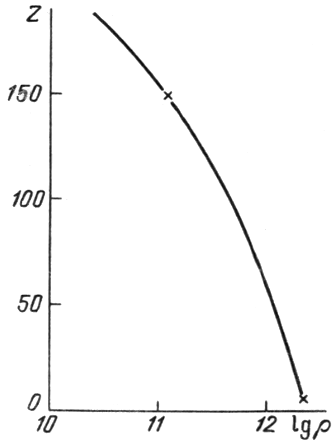
Utochnenie formuly dlya poverhnostnoi energii skazalos' tol'ko na izmenenii zaryada yadra \( Z\left( \rho \right) \), rost kotorogo zamedlilsya po sravneniyu s [265]. Na ris. 7 iz [266] privedeny rezul'taty rascheta \( Z\left( \rho \right) \) razlichnymi avtorami. Umen'shenie velichiny \( Z \) pri bol'shih plotnostyah privodit k bolee plavnomu izmeneniyu \( Z \) v processe fazovogo perehoda k odnorodnoi yadernoi materii. Nesovpadenie zavisimostei \( Z\left( \rho \right) \) u avtorov [256, 313, 504, 548] otrazhaet kak nedostatok fizicheskih znanii o zakonah vzaimodeistvii mezhdu nuklonami, tak i nesover shenstvo sushestvuyushih matematicheskih metodov rascheta.

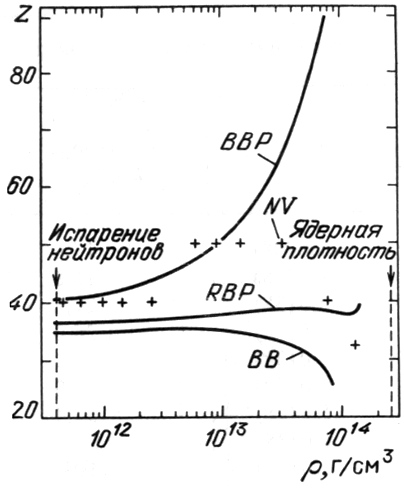Ris. 7. Zavisimost' zaryada $Z$ v kore neitronnoi zvezdy ot plotnosti, postroennaya po raschetam razlichnyh avtorov: VVR - [265], NV - [504], RBP - [548], VV - [313]

v) Plotnost', bol'she yadernoi.

Odnorodnaya yadernaya materiya (YaM), poyavlyayushayasya v rezul'tate fazovogo perehoda, sostoit iz neitronov s nebol'shoi primes'yu protonov i elektronov. Poka plotnost' YaM ne prevyshaet \( 2\rho _{0} \) ( \( \rho _{0}=2.8\cdot 10^{14}\mbox{~g}\cdot \mbox{sm}^{-3} \) - plotnost' svobodnoi YaM), dlya rascheta uravneniya sostoyaniya primenim metod Braknera-Bete-Goldstouna, osnovannyi na teorii vozmushenii [22]. Pri \( \rho \gt 2\rho _{0} \) raschety vedutsya s pomosh'yu variacionnogo principa, razrabotannogo Pandaripande [537]. Pri bol'shih plotnostyah uchityvaetsya rozhdenie tyazhelyh giperonov [9] i vozmozhnoe rozhdenie \( \pi ^{-} \)-mezonov (pionnaya kondensaciya [158]). Raschety uravneniya sostoyaniya yadernoi materii pri \( \rho \geq \rho _{0} \) vypolneny pri razlichnyh dopusheniyah v [275, 479]. V tabl. 9 iz [479] privoditsya uravnenie sostoyaniya dlya naibolee realisticheskogo varianta s parametrami potenciala vzaimodeistviya, uchityvayushimi eksperimental'nye dannye iz yadernoi fiziki vysokih energii, a takzhe rozhdenie giperonov. Vozmozhnoe poyavlenie pionnoi kondensacii slabo vliyaet na uravnenie sostoyaniya [275]. Sleduet imet' v vidu, chto s rostom plotnosti vse bolee vozrastaet neopredelennost' nashih znanii o fizike sil'nyh vzaimodeistvii i menee tochnymi stanovyatsya metody rascheta. V svyazi s etim dazhe v realisticheskom variante iz tabl. 9 pogreshnosti mogut dostigat' ~ 50%.

Kak otmechalos' vpervye Ya.B. Zel'dovichem [103, 110], trebovanie principa prichinnosti o tom, chto skorost' zvuka \( \nu _{s} \) ne dolzhna prevyshat' skorost' sveta \( c \), nakladyvaet ogranichenie na uravnenie sostoyaniya \( P\leq \epsilon =\rho c^{2} \). Vazhnost' etogo ogranicheniya svyazana s tem, chto ono deistvuet pri skol' ugodno bol'shih plotnostyah, gde o svoistvah yadernyh vzaimodeistvii izvestno ochen' malo.


Tablica 9. Realisticheskie parametry veshestva pri bol'shii plotnosti iz [479]
\( n_{b},\mbox{~sm}^{-3} \) \( \frac{E}{n_{b}}-m_{n}c^{2},\mbox{~MeV} \) \( \rho ,\mbox{~g}\cdot \mbox{sm}^{-3} \) \( P,\mbox{~din}\cdot \mbox{sm}^{-2} \)
1.0 (38) 12.6 1.70 (14) 1.19 (33)
1.5 (38) 16.6 2.55 (14) 2.93 (33)
2.0 (38) 21.2 3.42 (14) 6.00 (33)
2.5 (38) 26.0 4.31 (14) 1.09 (34)
3.0 (38) 32.2 5.21 (14) 1.83 (34)
4.0 (38) 46.9 7.04 (14) 4.09 (34)
5.0 (38) 64.4 8.95 (14) 7.61 (34)
6.0 (38) 83.7 1.09 (15) 1.26 (35)
7.0 (38) 109 1.31 (15) 1.99 (35)
8.0 (38) 134 1.54 (15) 2.85 (35)
9.0 (38) 160 1.76 (15) 3.71 (35)
1.0 (39) 189 2.01 (15) 4.02 (35)
1.1 (39) 215 2.26 (15) 5.02 (35)
1.25 (39) 254 2.66 (15) 6.76 (35)
1.4 (39) 295 3.08 (15) 8.81 (35)
1.5 (39) 324 3.37 (15) 1.03 (36)
1.7 (39) 383 4.00 (15) 1.38 (36)
2.0 (39) 475 5.04 (15) 2.02 (36)
2.5 (39) 639 7.02 (15) 3.40 (36)
3.0 (39) 814 9.36 (15) 5.20 (36)
Pri \( n_{b}\gt 1.0(39) \) imeyut mesto asimptoticheskie formuly
\( E=n_{b}\left( 15.05+3.03\left( \frac{n_{b}}{10^{39}}\right) ^{1.39}\right) \cdot 10^{-4} \mbox{erg}\cdot \mbox{sm}^{-3} \), \( P=403\left( n_{b}/10^{39}\right) ^{2.33}\cdot 10^{33} \mbox{din}\cdot \mbox{sm}^{-3} \),
\( \left( \rho =E/c^{2}\right) \).

g) Uchet konechnoi temperatury.

Uchet temperaturnyh effektov pri plotnostyah, kogda sushestvenno yadernoe vzaimodeistvie, sdelan dlya \( \rho \leq \rho _{0} \) s pomosh'yu obobsheniya metodov, primenyavshihsya pri issledovanii holodnogo veshestva [465] (sm. takzhe [314]). V ravnovesii rassmatrivalis' protony, neitrony, yadra geliya, odin tip tyazhelyh yader, dlya kotoryh nahodilsya minimum polnoi energii. Vvidu svobodnogo uleta neitrino i otsutstviya ravnovesiya po beta-processam, zadavalos' otnoshenie \( N_{p}/\left( N_{n}+N_{p}\right) =Y_{e} \). Vyrazheniya vseh vidov energii, vhodyashih v \( E_{tot} \) iz (4.6) i iz (4.8), zapisyvalis' s uchetom temperaturnyh popravok i k \( E_{tot} \) dobavlyalas' energiya dvizheniya yader, svyazannaya s konechnoi temperaturoi, a takzhe energii yader geliya. K nezavisimym velichinam, kotorye yavlyayutsya argumentami funkcii \( E_{tot} \) v (4.6), pri konechnoi temperature dobavlyayutsya \( n_{p} \) -koncentraciya svobodnyh protonov i \( n_{\alpha } \) - koncentraciya yader geliya, kotoraya opredelyaetsya iz usloviya ravnovesiya otnositel'no razbieniya na protony i neitrony tipa (3.3), no s uchetom konechnogo ob'ema (zadavaemogo) yader geliya. Dlya opredeleniya \( n_{p} \) dobavlyalos' uslovie ravnovesiya po obmenu protonami mezhdu yadrami i protonami v gaze. Na ris.8 iz [456] predstavleny himicheskie svoistva pri bol'shih temperaturah i plotnostyah dlya \( Y_{e}=0.25 \). Interesno, chto pri bol'shih plotnostyah \( \rho \gt 10^{14}\mbox{~g}\cdot \mbox{sm}^{-3} \), kogda yadra nachinayut zanimat' bol'she poloviny ob'ema, vmesto yader, pogruzhennyh v menee plotnyi nuklonnyi gaz, voznikayut shariki menee plotnogo veshestva (puzyri), pogruzhennye v bolee plotnuyu yadernuyu materiyu. Vazhnyi vyvod, sleduyushii iz dannyh raschetov, sostoit v sohranenii yader do ochen' vysokih temperatur \( \sim 20\mbox{~MeV}\approx 2\cdot 10^{11}\mbox{~K} \), chto yavlyaetsya sledstviem ucheta yadernyh vzaimodeistvii i vliyaniya okruzhayushego gaza na svoistva yader. V [456] otmechalos', chto diagramma na ris. 8 malo chuvstvitel'na k izmeneniyu \( Y_{e} \) v predelah \( 0.2\leq Y_{e}\leq 0.5 \). Uchet razlichnyh tipov tyazhelyh yader, odnovremenno prisutstvuyushih v ravnovesii [346], takzhe slabo vliyaet na poluchennye rezul'taty [456]. Na ris. 9 i 10 iz [456] privedeny izentropy veshestva i zavisimost' pokazatelya adiabaty \( \gamma _{1}\left( \rho \right) \) dlya etih izentrop. Vidno, chto sushestvovanie yader zametno umen'shaet \( \gamma _{1} \) po sravneniyu s nuklonnym gazom pri nenulevoi entropii. Kak vidno iz ris. 8, pri plotnosti, bol'she yadernoi, veshestvo vsegda odnorodno.

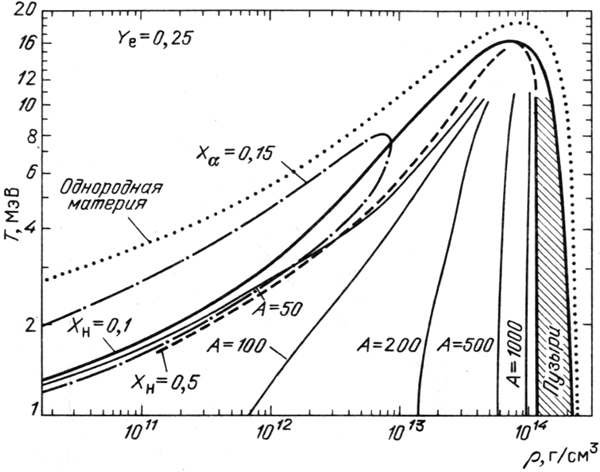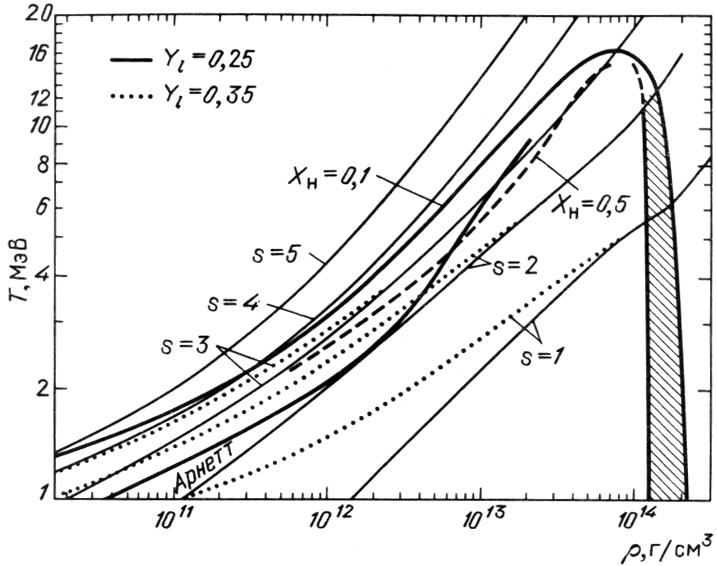Ris. 8. Himicheskie svoistva veshestva pri vysokih temperaturah i plotnostyah dlya $Y_e$ = 0,25 iz [456]. Sploshnaya liniya ogranichivaet oblast', gde vesovaya dolya yader $X_H$ > 0,1, a v oblasti vnutri shtrihovoi linii $X_H$ > 0,5. V oblasti vnutri shtrih-punktirnoi linii vesovaya dolya geliya $X_H$ > 0,15. Tonkie sploshnye linii zadayut massy yader. Zashtrihovana oblast' sushestvovaniya puzyrei. Punktirnaya liniya opredelyaet granicu ustoichivosti odnorodnoi materii otnositel'no razbieniya na dve fazy

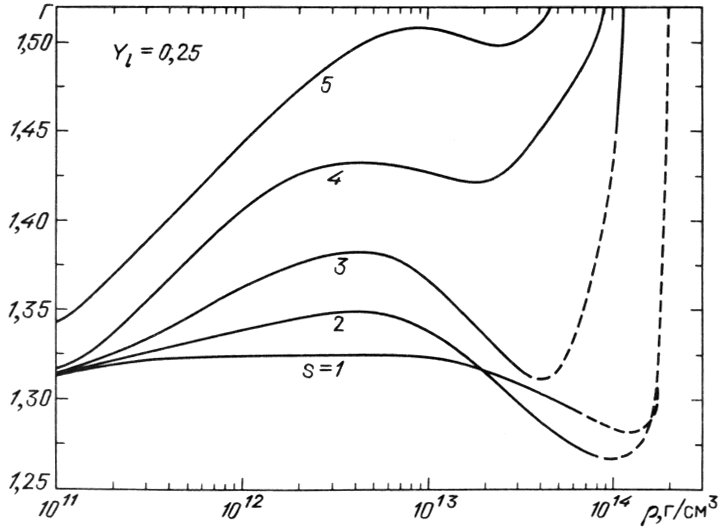Ris. 9. Adiabaty s ukazannymi znacheniyami bezrazmernoi entropii $s$ (v edinicah $k/m_u$) dlya $Y_L$ = 0,25 (sploshnye linii) i $Y_l$ = 0,35 (punktirnye linii), iz [456]. Linii $X_H$ = 0,1 i $X_H$ = 0,5 imeyut tot zhe smysl, chto i na ris. 8. Pri $\rho$ > 1012 g/sm3 veshestvo neprozrachno dlya neitrino i sohranyaetsya velichina $Y_l$ - leptonnyi zaryad na odin barion. Ukazana takzhe traektoriya centra zvezdy pri kollapse, poluchennaya Arnettom [255a]

Ris. 10. Zavisimost' pokazatelya adiabaty $G = \gamma_1 = (\partial\ln P/\partial\ln\rho)_S$ ot plotnosti $\rho$ dlya ukazannyh znachenii bezrazmernoi entropii $s$ (sm. ris. 9) pri $Y_l$ = 0,25 iz [456]. V oblasti shtrihovyh linii krivye $\gamma(\rho)$ privedeny sglazhennymi bez nekotoryh nesushestvennyh detalei

Energiya Fermi ideal'nogo neitronnogo gaza, opredelyaemaya analogichno (2.21), est'


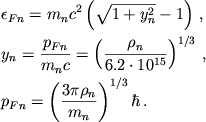\begin{displaymath} \eqalign{ & \epsilon _{Fn}=m_{n}c^{2}\left( \sqrt{1+y_{n}^{2}}-1\right)\,, \cr & y_{n}=\frac{p_{Fn}}{m_{n}c}=\left( \frac{\rho _{n}}{6.2\cdot 10^{15}}\right)^{1/3}\,, \cr & p_{Fn}=\left( \frac{3\pi \rho _{n}}{m_{n}}\right) ^{1/3}\hbar\,. \cr } \end{displaymath} (4.10)

Pri \( \rho \approx \rho _{n}\geq \rho _{0} \) imeem \( y_{n}\geq 0.36 \) i \( \epsilon _{Fn}\geq 61\mbox{~MeV} \). Maksimal'nye temperatury, dostigaemye pri gravitacionnom kollapse, obychno ne prevyshayut \( \sim 20\mbox{~MeV} \), poetomu pri \( \rho \geq \rho _{0} \) temperaturnye popravki k uravneniyu sostoyaniya nesushestvenny.

d) Neravnovesnaya neitronizaciya pri uvelichenii plotnosti v holodnom veshestve.

Ravnovesie po yadernomu sostavu dostigaetsya v veshestve pri vysokih temperaturah, kogda otkryty vse kanaly reakcii. Po mere ostyvaniya, bol'shinstvo kanalov reakcii zakryvaetsya i v holodnom veshestve dostizhenie SME, strogo govorya, nevozmozhno. Veshestvo pri malyh temperaturah vsegda nahoditsya v neravnovesnom sostoyanii, odnako stepen' ne ravnovesnosti i harakter ee zavisyat ot puti, kotorym veshestvo prishlo k sostoyaniyu s dannymi \( \rho \) i \( T \). V [60, 61, 287] rassmotreny dva vozmozhnyh puti: szhatie holodnogo veshestva i ostyvanie veshestva pri dannoi plotnosti s neravnovesnymi sostavami, voznikayushimi pri etom.

Rassmotrim szhatie holodnogo veshestva. Pust' pri malyh \( \rho \) veshestvo sostoit iz samogo stabil'nogo elementa \( ^{56}Fe \) i medlenno szhimaetsya pri temperature, blizkoi k nulyu. Kogda plotnost' dostigaet velichiny \( 1.24\cdot 10^{9}\mbox{~g}\cdot \mbox{sm}^{-3} \), \( \epsilon _{Fe}=3.81\mbox{~MeV} \), stanovitsya energeticheski vygodnym zahvat elektrona yadrom \( ^{56}Fe \)7. Vvidu men'shei ustoichivosti nechetno-nechetnyh yader, za pervym zahvatom srazu sleduet vtoroi i idet cepochka reakcii

\begin{displaymath} ^{56}Fe+e^{-}\rightarrow ^{56}Mn+\nu _{e} , \quad ^{56}Mn+e^{-}\rightarrow ^{56}Cr+\nu _{e} . \end{displaymath} (4.11)

Dlya vtoroi reakcii iz (4.11) velichina \( \epsilon _{\beta }=1.6\mbox{~MeV} \) [99]. Pri \( \epsilon _{Fe}=3.81\mbox{~MeV} \) ona prohodit neravnovesno i soprovozhdaetsya nagrevom ([56], sm. gl. 5), kotorym prenebregaem vvidu togo, chto on ne vliyaet na formirovanie himicheskogo sostava. Posle obrazovaniya \( ^{56}Cr \) v hode dal'neishego szhatiya stanovyatsya energeticheski vygodnymi prevrasheniya \( ^{56}Cr\rightarrow ^{56}K\rightarrow ^{56}Ar \) i t.d., poka ne obrazuetsya yadro s energiei otryva poslednego neitrona, blizkoi k nulyu \( Q_{n}\approx 0 \). Posle etogo povyshenie plotnosti i zahvat elektronov soprovozhdayutsya holodnym ispareniem neitronov iz yader i umen'sheniem \( A \) naryadu s \( Z \). Vvidu razlichiya v svoistvah chetnyh i nechetnyh yader, chast' isparyayushihsya neitronov unosit energiyu $\sim$1 MeV/neitron, idushuyu na nagrev veshestva [78].

V processe neravnovesnoi neitronizacii chislo yader, prihodyashihsya na odin barion, ne menyaetsya. Esli \( A_{0} \)- atomnaya massa nachal'nogo yadra, to pri dannoi plotnosti koncentracii yader i elektronov (s uchetom elektroneitral'nosti) zapishutsya v vide


\begin{displaymath} n_{A,Z}=\frac{\rho }{A_{0}m_{u}} , \quad n_{e}=\frac{Z\rho }{A_{0}m_{u}} . \end{displaymath} (4.12)

Zdes' massa yadra priblizhenno prinyata ravnoi \( Am_{u} \), a plotnost' \( \rho =Nm_{u} \), \( N=N_{n}+N_{p} \) polnaya koncentraciya barionov. Do nachala ispareniya neitronov pri \( A=A_{0} \) zaryad yadra \( Z \) ostaetsya postoyannym v intervale plotnostei, gde vypolnyaetsya neravenstvo


\begin{displaymath} \epsilon _{\beta }\left( A_{0},Z+2\right) \lt \epsilon _{Fe}\left( n_{e}\right) \lt \epsilon _{\beta }\left( A_{0},Z\right) . \end{displaymath} (4.13)

Kogda pervoe sootnoshenie v (4.13) obrashaetsya v ravenstvo, nachinaetsya ocherednoi zahvat elektrona pri postoyannyh \( \epsilon _{Fe} \) i \( P_{e} \) v intervale plotnostei \( \rho _{Z+2}\lt \rho \lt \rho _{Z} \):

\begin{displaymath} \eqalign{ & \epsilon _{Fe}\left( n_{e}\right) =\epsilon _{\beta }\left( A_{0},Z+2\right) =\mbox{const}, \cr & \frac{\rho _{Z}}{\rho _{Z+2}}=\frac{Z+2}{Z}\,. \cr } \end{displaymath} (4.14)

Svoistva veshestva pri holodnoi neitronizacii do nachala ispareniya neitronov privedeny v tabl. 10, gde ispol'zovalis' yadernye dannye iz [379]. Posle nachala ispareniya neitronov koncentraciya ih opredelyaetsya sootnosheniem


\begin{displaymath} n_{n}=\frac{\rho }{m_{u}}\left( 1-\frac{A}{A_{0}}\right) , \quad m_{n}\approx m_{p}\approx m_{u} . \end{displaymath} (4.15)

Isparenie neitrona iz yadra pri nalichii svobodnyh neitronov dopustimo, esli energiya vyletayushih neitronov prevyshaet ih energiyu Fermi (4.10). Uslovie ispareniya posle ocherednogo zahvata elektrona v usloviyah (4.14) zapishetsya v vide


\begin{displaymath} Q_{n}\left( A,Z\right) =B_{A,Z}-B_{A-1,Z}\leq -\epsilon _{Fn}\left( n_{n}\right) . \end{displaymath} (4.16)

Vvidu kolebaniya funkcii \( Q_{n}(A,Z) \) v zavisimosti ot chetnosti \( A \) i \( Z \), protekaet srazu cepochka reakcii


\begin{displaymath} \eqalign{ & \left( A,Z\right) +e^{-}\rightarrow \left( A,Z-1\right) +\nu _{e}\rightarrow \left( A-k_{1},Z-1\right) +k_{1}n+\nu _{e}\,, \cr & \left( A-k_{1},Z-1\right) +e^{-}\rightarrow \left( A-k_{1},Z-2\right) +\nu _{e}\rightarrow \left( A-k_{1}-k_{2},Z-2\right) +k_{2}n+\nu _{e}\,, \cr } \end{displaymath} (4.17)

gde \( k_{1}\approx k_{2}=3\div 4 \) dlya razlichnyh yader [560]. Raschet neravnovesnoi neitronizacii s ispareniem neitronov po sisteme uravnenii (4.12)-(4.16) provodilsya v [78] s energiei svyazi po formule Veiczekkera, a v [560] s uchetom yadernogo vzaimodeistviya nuklonov i vychislenii energii svyazi po metodike raboty [265] pri dopolnitel'nom uchete vliyaniya yadernyh obolochek. Rezul'taty etih raschetov privedeny v tabl. 10.


Tablica 10. Svoistva veshestva pri holodnoi neitronizacii yader zheleza
\( \rho, 10^{11}\mbox{~g}\cdot \mbox{sm}^{-3} \) \( A \); \( Z \) \( \epsilon _{Fe},\mbox{~MeV} \) \( \epsilon _{Fn},\mbox{~MeV} \) \( P,10^{30}\mbox{~din}\cdot \mbox{sm}^{-2} \) \( P_{\mbox{p}},10^{30}\mbox{~din}\cdot \mbox{sm}^{-2} \)
0.012 56; 24 3.81 0 5.5 (-4) 0
0.14 56; 22 8.83 0 0.014 0
0.57 56; 20 14.0 0 0.080 0
1.6 56; 18 19.3 0 0.28 0
3.098 54; 18 23.84 0.069 0.569 3(-4) (6.5)
3.9 56; 16 25.2 0 0.73 0
5.01 56; 16 26.98 0 0.933  
6.17 54; 16 28.85 0.09 1.20  
6.233 48; 16 29.52 0.232 1.25 0.0059 (5.7)
7.24 46; 16 29.19 0.26 1.29  
7.664 42; 14 29.66 0.468 1.41 0.0344 (3.6)
9.689 36; 12 30.47 0.693 1.75 0.0921 (4.1)
10.1 56; 14 31.78 0 1.97 0
10.23 40; 12 31.00 0.44 1.66  
12.1 48; 12 32.06 0.43 2.07 0.029
12.88 35; 10 31.60 0.58 1.86  
14.13 32; 9 31.47 0.65 1.86  
14.88 30; 10 31.36 0.987 2.12 0.422 (4.5)
15.0 40; 10 32.35 0.79 2.25 0.13
16.8 36; 9 32.50 0.9 2.38 0.23
17.43 24; 8 32.47 1.41 2.48 0.537 (5.2)
19.2 32; 8 32.64 1.22 2.59 0.39
22.2 28; 7 32.78 1.49 2.88 0.65
25.65 18; 6 33.47 2.04 3.57 1.36 (6.0)
26.3 24; 6 32.92 1.82 3.35 1.07
44.12 12; 4 35.38 2.52 6.06 3.31 (7.8)
\( P \) - polnoe davlenie, \( P_{n} \) - davlenie neitronov; sleva v stolbcah dany rezul'taty iz [78], sprava - iz [560], gde $P_n$ ne privoditsya. V seredine dany rezul'taty rascheta s ispol'zovaniem tablic [379, 135] do nachala ispareniya neitronov i formuly (4.20). V poslednem stolbce v skobkah dana temperatura \( T(10^{9}K) \) pri obrazovanii dannogo sostava za schet neravnovesnyh \( \beta \)-zahvatov iz [78].

V [560] otmechena vazhnost' piknoyadernyh reakcii v hode holodnoi ne ravnovesnoi neitronizacii vvidu togo, chto skorost' etih reakcii bystro rastet s rostom plotnosti (sm. gl. 4). Pri \( \rho =1.4\cdot 10^{12}\mbox{~g}\cdot \mbox{sm}^{-3} \) yadra s \( \left( A,Z\right) =\left( 32,9\right) \), obrazuyushiesya iz yader \( ^{56}Fe \), slivayutsya i posle zahvata dvuh elektronov i ispareniya vos'mi neitronov, obrazuyutsya yadra s \( \left( A,Z\right) =\left( 56,16\right) \). V [560] ne rassmatrivalsya teplovoi effekt etoi i posleduyushih reakcii sliyaniya. Holodnaya neravnovesnaya neitronizaciya dovedena do \( \rho =5.13\cdot 10^{13}\mbox{~g}\cdot \mbox{sm}^{-3} \) s obrazovaniem yadra \( \left( 99,19\right) \) (sr. s yadrom \( \left( 375,74\right) \) iz tabl. 8 ili \( Z=30\div 40 \) iz ris. 7 dlya ravnovesnogo sostava pri toi zhe plotnosti). Ne isklyucheno, chto vydelenie tepla pri piknoyadernyh reakciyah s posleduyushim bystrym neravnovesnym zahvatom elektronov i ispareniem neitronov mozhet dostatochno povysit' temperaturu dlya ustanovleniya yadernogo sostava, blizkogo k ravnovesnomu.

Energiya otryva poslednego protona

\begin{displaymath} Q_{p}\left( A,Z\right) =B_{A,Z}-B_{A-1,Z-1}=\epsilon _{\beta }\left( A,Z\right) +Q_{n}\left( A,Z-1\right) -\left( m_{n}-m_{p}\right) c^{2}+m_{e}c^{2} \end{displaymath} (4.18)

na granice \( Q_{n}=0 \) issledovalas' P.E. Nemirovskim, ocenki kotorogo privedeny na ris. 11. Grubo eta zavisimost' approksimiruetsya formuloi [61]
\begin{displaymath} Q_{p}=\left( 33-\frac{Z}{7}\right) \mbox{~MeV} , \quad A=4Z \mbox{~pri~} Q_{n}=0 , \quad Z\geq 6 \end{displaymath} (4.19)

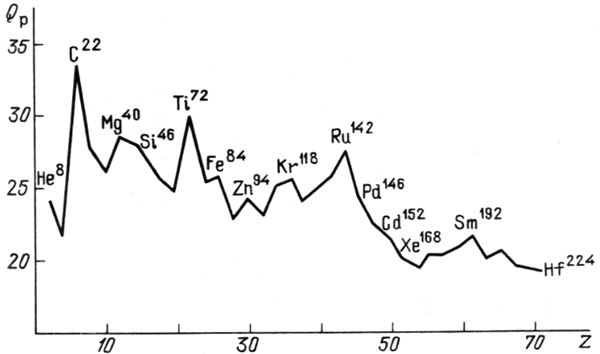Ris. 11. Energiya otryva protona $Q_p$ v zavisimosti ot $Z$ dnya yader, lezhashih na granice sushestvovaniya s $Q_n$ = 0. Zavisimost' postroena soglasno kolichestvennym ocenkam P.E. Nemirovskogo

Prenebregaya energiei Fermi svobodnyh neitronov i schitaya, chto neitronizaciya s ispareniem neitronov idet vdol' linii \( Q_{n}=0 \), poluchim iz (4.14) s uchetom (2.21), (4.12) i (4.19) sootnoshenie dlya opredeleniya \( Z\left( \rho \right) \), \( A\left( \rho \right) \) :

\begin{displaymath} \left[ 1+\left( \frac{Z_{\rho }}{10^{6}A_{0}}\right) ^{2/3}\right] ^{^{1/2}}=1.96\left( 33-\frac{Z}{7}\right) +2.53 ; \quad A=4Z \end{displaymath} (4.20)

Zdes' uchteno, chto \( m_{e}c^{2}=0.511\) MeV, \( \left( m_{n}-m_{p}\right) c^{2}=1.293\) MeV. Raschety s ispol'zovaniem (4.20) takzhe privedeny v tabl. 10, otkuda vidno, chto razlichie v davlenii \( P\left( \rho \right) \) dlya vseh treh sposobov ne prevyshaet 20%. V to zhe vremya eto davlenie bolee chem v poltora raza prevyshaet ravnovesnoe davlenie pri toi zhe plotnosti (tabl. 7).

e) Neravnovesnyi sostav pri ostyvanii goryachego plotnogo veshestva.

Kogda temperatura v ostyvayushem veshestve stanet men'she \( \left( 4-5\right) \cdot 10^{9}K \), reakcii mezhdu zaryazhennymi chasticami rezko zamedlyayutsya i koncentraciya yader zamorazhivaetsya. V etih usloviyah vozmozhno protekanie reakcii s neitronami, fotootsheplenie i zahvat neitronov, \( e^{-} \) raspady pri \( \epsilon _{\beta }\gt \epsilon _{Fe} \) i \( e^{-} \)-zahvaty pri \( \epsilon _{\beta }\lt \epsilon _{Fe} \). V usloviyah kineticheskogo ravnovesiya po beta-processam (3.6) s \( \frac{dN_{n}}{dt}=0 \), v veshestve imeetsya bol'shoi izbytok svobodnyh neitronov [224]. Pri konechnoi temperature yadra mogut prisoedinyat' neitrony i otsheplyat' ih, esli

\begin{displaymath} -\epsilon _{Fn}\lt Q_{n}\lt Q_{nb}\approx 20kT-\epsilon _{Fn} . \end{displaymath} (4.21)

V usloviyah izbytka neitronov \( x_{n}\gt 0.5 \) process formirovaniya neravnovesnogo himicheskogo sostava pri bystrom ostyvanii veshestva predstavlen na ris. 12 iz [61, 287]. Ploskost' \( \left( A,Z\right) \) dlya yader razbita na tri oblasti:

    I oblast' s \( Q_{n}\gt Q_{nb} \),

    II oblast' s \( -\epsilon _{Fn}\lt Q_{n}\lt Q_{nb} \), \( \epsilon _{\beta }\gt \epsilon _{Fe} \).

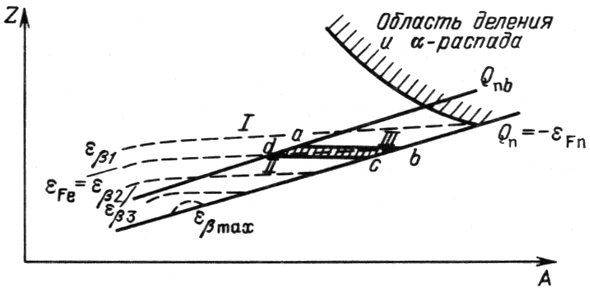    III oblast' s \( -\epsilon _{Fn}\lt Q_{n}\lt Q_{nb} \), \( \epsilon _{\beta }\lt \epsilon _{Fe} \).

Ris. 12. Obrazovanie himicheskogo sostava pri ostyvanii na stadii ogranichennogo ravnovesiya. Liniya $Q_n = -\epsilon_{Fn}$ otdelyaet oblast' sushestvovaniya yader. Liniya $Q_nb$, razdelyaet oblast' I, gde nevozmozhno fotootsheplenie neitronov, i oblasti II i III. Shtrihovye linii - urovni postoyannogo $\epsilon_\beta, \epsilon_\beta1 < \epsilon_\beta2 < \ldots < \epsilon_\beta,\max$. V oblasti I $Q_n > Q_nb$, v oblasti II $Q_n < Q_nb$, $\epsilon_Fn < \epsilon_\beta$, v oblasti III $Q_n < Q_nb$, $\epsilon_Fn < \epsilon_\beta$. Liniya so shtrihovkoi sprava otdelyaet oblast' deleniya i al'fa-raspada. Zashtrihovannaya oblast' abed opredelyaet granicy znachenii (A, Z) pri ogranichennom ravnovesii s dannymi $Q_nb(T)$ i $\epsilon_Fn(\rho)$

Pri vysokoi koncentracii neitronov sushestvuyushie yadra bystro pereidut iz oblasti I v oblasti II i III iz-za neitronnogo zahvata. V oblastyah II i III imeetsya ravnovesie po otnosheniyu k zahvatu i otshepleniyu neitronov. V oblasti II beta-raspady privodyat k rostu Z i yadra perehodyat v oblast' vyshe linii \( cd \). V oblasti III beta-zahvaty umen'shayut \( Z \) i perevodyat yadra v oblast' nizhe linii \( ab \). Takim obrazom, v usloviyah ogranichennogo ravnovesiya pri \( \epsilon _{Fe}\gg Q_{nb}\gg kT \), kogda temperaturnye effekty ne vliyayut na beta-processy, yadernyi sostav opredelyaetsya uzkoi oblast'yu aecd na ploskosti \( (A,Z) \) (ris. 12). Vyhod za predely etoi oblasti ne proishodit iz-za otsutstviya dopustimyh beta-processov i fotootsheplenii neitronov. Pri \( T\leq 5\cdot 10^{8}K \) ostaetsya tol'ko odno yadro na granice (4.16).

Esli prenebrech' \( \epsilon _{Fn} \) i uchest' (4.18) i (4.19), to yadernyi sostav mozhno priblizhenno naiti iz sootnoshenii, analogichnyh (4.20),

\begin{displaymath} A=4Z , \quad Z=7\left\{ 33-0.511\left[ \left( \frac{\rho }{\mu _{Z}10^{6}}\right) ^{2/3}+1\right] ^{1/2}+1.293\right\} . \end{displaymath} (4.22)

Zavisimost' \( Z(\rho ) \) pri \( x_{n}=1/2 \) privedena na ris. 13. Pri \( \rho =\rho _{2}=2.24\cdot 10^{12}\mbox{~g}\cdot \mbox{sm}^{-3} \) obrazuetsya yadro s \( Z=6 \), obladayushee \( \epsilon _{\beta ,\max} \), a pri \( \rho =\rho _{1}=1.2\cdot 10^{11}\mbox{~g}\cdot \mbox{sm}^{-3} \) obrazuetsya yadro s \( Z=150 \), dlya kotorogo \( Z^{2}/A=Z/4=37.5 \) i [164] vremya deleniya, zavisyashee ot \( Z^{2}/A \), est' \( \tau _{f}=3\cdot 10^{7} \) let. Pri \( \rho \lt \rho _{1} \) velichina \( Z^{2}/A \) rastet, a vremya deleniya umen'shaetsya. Yadernoe delenie, a takzhe al'fa-raspad privodyat k rostu chisla zarodyshevyh yader. Takim obrazom, pri \( \rho \gt \rho _{2} \) ili \( \rho \lt \rho _{1} \) himicheskii sostav mozhet priblizit'sya k ravnovesnomu v sostoyanii SME. Sushestvennaya neravnovesnost' pri ostyvanii vozmozhna tol'ko pri \( \rho _{1}\lt \rho \lt \rho _{2} \).

Ris. 13. Zavisimost' $Z(p)$ iz (4.22) dlya neravnovesnogo sostava, obrazuyushegosya pri ostyvanii plotnogo veshestva, dlya $x_n$ = 1/2. Krestikami ukazany primernye granicy neravnovesnosti

Otlichie neravnovesnosti, obrazuyusheisya pri ostyvanii, ot toi, kotoraya obrazuetsya pri holodnoi neitronizacii, imeetsya, v osnovnom, pri men'shih plotnostyah, gde dlya goryachego sluchaya poluchayutsya ochen' bol'shie \( Z \), sm. tabl. 10 i ris. 13. V to zhe vremya v oboih variantah imeyutsya principial'nye otlichiya ot SME, gde \( Z(\rho ) \) uvelichivaetsya s rostom plotnosti, v to vremya kak v oboih neravnovesnyh sostavah \( Z(\rho ) \) bystro padaet s rostom plotnosti.

zh) Termodinamicheskie svoistva veshestva pri uchete kulonovskogo vzaimodeistviya. Kulonovskie vzaimodeistviya v obychnom veshestve yavlyayutsya osnovnymi, opredelyayushimi agregatnoe sostoyanie, stepeni ionizacii i popravki k termodinamicheskim funkciyam. V razrezhennyh gazah vzaimodeistviya v osnovnom lokalizovany vnutri atomov i nepolnost'yu obodrannyh ionov. Pri nahozhdenii stepeni ionizacii po formule Saha (1.8) proishodit priblizhennyi uchet etogo vzaimodeistviya.

Osnovnym parametrom, harakterizuyushim stepen' ionizacii v razrezhennyh gazah, yavlyaetsya velichina \( \lambda _{ij}=I_{ij}/kT \) (sm. 1). Pri umen'shenii temperatury i roste \( \lambda _{ij} \) gaz stanovitsya neitral'nym, a zatem, kogda teplovaya energiya stanet men'she energii vzaimodeistviya mezhdu atomami, prevratitsya snachala v zhidkoe, a zatem v tverdoe kristallicheskoe telo s uporyadochennoi strukturoi, obladayushei minimumom energii8. Pri szhatii veshestva srednee rasstoyanie mezhdu atomami \( l=n^{-1/3}_{A}=Z^{1/3}n^{-1/3}_{e} \) umen'shaetsya9 i pri \( \rho =\rho _{i1} \) stanovitsya poryadka razmera atoma \( a_{Z}=Z^{-1/3}a_{0} \) v modeli Tomasa-Fermi (TF) [555], \( a_{0}=\hbar ^{2}/m_{e}e^{2} \) - Borovskii radius. Pri \( \rho =\rho _{i1} \) nachinaetsya ionizaciya davleniem. Veshestvo stanovitsya polnost'yu ionizovannym pri \( \rho =\rho _{i2} \). kogda mezhelektronnye rasstoyaniya stanovyatsya poryadka radiusa blizhaishei k yadru elektronnoi orbity \( a_{Z0}=a_{0}Z^{-1} \) [71]. Plotnost' \( \rho _{i1} \) nahoditsya s uchetom (2.21) iz sootnosheniya

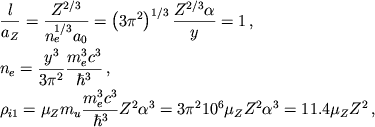\begin{displaymath} \eqalign{ & \frac{l}{a_{Z}}=\frac{Z^{2/3}}{n^{1/3}_{e}a_{0}}=\left( 3\pi ^{2}\right) ^{1/3}\frac{Z^{2/3}\alpha }{y}=1\,, \cr & n_{e}=\frac{y^{3}}{3\pi ^{2}}\frac{m^{3}_{e}c^{3}}{\hbar ^{3}}\,, \cr & \rho _{i1}=\mu _{Z}m_{u}\frac{m^{3}_{e}c^{3}}{\hbar ^{3}}Z^{2}\alpha ^{3}=3\pi ^{2}10^{6}\mu _{Z}Z^{2}\alpha ^{3}=11.4\mu _{Z}Z^{2}\,, \cr } \end{displaymath} (4.23)

\( \alpha =e^{2}/\hbar c=1/137 \) - postoyannaya tonkoi struktury. Analogichno dlya plotnosti \( \rho _{i2} \) imeem
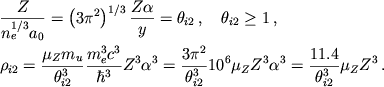\begin{displaymath} \eqalign{ & \frac{Z}{n^{1/3}_{e}a_{0}}=\left( 3\pi ^{2}\right) ^{1/3}\frac{Z\alpha }{y}=\theta _{i2}\,, \quad \theta _{i2}\geq 1\,, \cr & \rho_{i2}=\frac{\mu _{Z}m_{u}}{\theta _{i2}^{3}}\frac{m^{3}_{e}c^{3}}{\hbar ^{3}}Z^{3}\alpha ^{3}=\frac{3\pi ^{2}}{\theta _{i2}^{3}}10^{6}\mu _{Z}Z^{3}\alpha ^{3}=\frac{11.4}{\theta _{i2}^{3}}\mu _{Z}Z^{3}\,. \cr } \end{displaymath} (4.24)

Otmetim, chto pri \( Z\lt \frac{\theta }{\alpha \left( 3\pi ^{2}\right) ^{1/2}}\approx 44\theta _{i2} \) polnaya ionizaciya davleniem proishodit pri nerelyativistskih elektronah. Dlya zheleza \( ^{56}Fe \) imeem \( \rho _{i1}=1.7\cdot 10^{4}\mbox{~g}\cdot \mbox{sm}^{-3} \), \( \rho _{i2}=4.4\cdot 10^{5}\theta _{i2}^{-3}\mbox{~g}\cdot \mbox{sm}^{-3} \).

Rassmotrim fazovye prevrasheniya i kulonovskie popravki k termodinamicheskim funkciyam v plotnom, polnost'yu ionizovannom veshestve. V vidu malosti parametra \( \beta _{Z}=\frac{Z^{2/3}}{n^{1/3}_{e}a_{0}}\left( \approx \frac{E_{c}}{Z\epsilon _{Fe}}\right) \) popravki pri \( T=0 \) mozhno nahodit' metodom posledovatel'nyh priblizhenii [3,555]. Osnovnuyu popravku k kineticheskoi energii elektronov daet elektrostaticheskoe vzaimodeistvie ionov v reshetke i svobodnyh elektronov mezhdu soboi, a takzhe obmennoe vzaimodeistvie elektronov. V pervom priblizhenii elektrony mozhno schitat' raspolozhennymi odnorodno. Energiya elektrostaticheskogo vzaimodeistviya \( E_{c} \) naibolee prosto rasschityvaetsya v priblizhenii Vignera-Zeica (\( WS \)), gde uchityvaetsya tol'ko vzaimodeistvie ionov i elektronov vnutri sfericheskoi yacheiki radiusa $l_{WS}$

\begin{displaymath} \frac{4\pi }{3}l^{3}_{WS}=n_{A,Z}^{-1} , \quad l_{WS}=\left( \frac{3}{4\pi }\right) ^{1/3}l . \end{displaymath} (4.25)

Energiya na odno yadro \( E_{c} \) v dannom priblizhenii est' [3, 555]


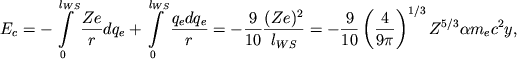\begin{displaymath} E_{c}=-\int\limits _{0}^{l_{WS}}\frac{Ze}{r}dq_{e}+\int\limits^{l_{WS}}_{0}\frac{q_{e}dq_{e}}{r}=-\frac{9}{10}\frac{(Ze)^{2}}{l_{WS}}=-\frac{9}{10}\left( \frac{4}{9\pi }\right) ^{1/3}Z^{5/3}\alpha m_{e}c^{2}y , \end{displaymath} (4.26)

gde \( q_{e}=\frac{4\pi }{3}en_{e}r^{3} \) - summarnyi elektricheskii zaryad elektronov vnutri radiusa \( r \), uchteno takzhe sootnoshenie \( l_{WS}=\left( \frac{9\pi }{4}\right) ^{1/3}\frac{\hbar }{m_{e}c}\frac{Z^{1/3}}{y} \)10. V [555] uchityvaetsya popravka sleduyushego poryadka za schet neodnorodnosti elektronnoi plotnosti vnutri yacheiki v TF priblizhenii. Eta popravka sostoit iz popravki k energii Fermi \( E_{TF} \) i korrelyacionnoi popravki k elektrostaticheskoi energii \( E_{cor} \):
\begin{displaymath} \eqalign{ & E_{TF}=-\frac{162}{175}\left( \frac{4}{9\pi }\right) ^{2/3}\sqrt{1+y^{2}}Z^{7/3}\alpha ^{2}m_{e}c^{2}\,, \cr & E_{cor}=\left[ 0.031\ln \left( \frac{e^{2}m_{e}}{\hbar ^{2}}l_{WS}\right) -0.048\right] Z\alpha ^{2}m_{e}c^{2}\,. \cr } \end{displaymath} (4.27)

Poslednii chlen stanovitsya sushestvennym pri umen'shenii plotnosti. Energiya obmennogo vzaimodeistviya v obshem sluchae est' [555]


\begin{displaymath} E_{ex}=-\frac{3Z}{4\pi }\alpha m_{e}c^{2}y\varphi \left( y\right) , \end{displaymath}


\begin{displaymath} \hbox{% \begin{tabular}{l} $\displaystyle{ \varphi \left( y\right) =\frac{1}{4y^{4}}\left[ \frac{9}{4}+3\left( \beta ^{2}-\frac{1}{\beta ^{2}}\right) \ln \beta -6\left( \ln \beta \right) ^{2}-\left( \beta ^{2}+\frac{1}{\beta ^{2}}\right) -\frac{1}{8}\left( \beta ^{4}+\frac{1}{\beta ^{4}}\right) \right] , }$ \\ $\displaystyle{ \beta =y+\sqrt{1+y^{2}} ; }$ \\ $\displaystyle{ \varphi \left( y\right) = \left\{ \begin{array}{cl} 1 & \quad \mbox{pri~} y\ll 1 , \\ -1/2 & \quad \mbox{pri~} y\gg 1 . \\ \end{array} \right. }$ \\ \end{tabular}} \end{displaymath} (4.28)

V nerelyativistskom predele \( E_{ex} \) privedena v [3]. Takim obrazom, osnovnye popravki k kineticheskoi energii holodnogo gaza (2.22) za schet kulonovskogo vzaimodeistviya dlya edinicy massy ravny s uchetom (2.19)

\begin{displaymath} \eqalign{ E_{q}=&\frac{1}{Am_{u}}\left( E_{c}+E_{TF}+E_{cor}+E_{ex}\right) = \cr & =\left\{ -\frac{3}{10\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{1/3}\alpha Z^{2/3}y-\frac{54}{175\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{2/3}\alpha ^{2}Z^{4/3}\sqrt{1+y^{2}}+ \right. \cr & \left. +\frac{0.031\alpha ^{2}}{3\pi ^{2}}\ln \left[ \left( \frac{9\pi }{4}\right) ^{1/3}\frac{\alpha Z^{1/3}}{y}\right] -\frac{0.016}{\pi ^{2}}\alpha ^{2}-\frac{\alpha }{4\pi ^{3}}y\varphi \left( y\right) \right\} \frac{m^{4}_{e}c^{5}}{\hbar ^{3}}\frac{y^{3}}{\rho }\,. \cr } \end{displaymath} (4.29)

Iz termodinamicheskogo sootnosheniya \( P=\rho ^{2}\frac{dE}{dp} \), \( \frac{dy}{dp}=\frac{1}{3}\frac{y}{\rho } \) nahodim popravku k davleniyu

\begin{displaymath} \eqalign{ P_{q}& =P_{c}+P_{TF}+P_{cor}+P_{ex}= \cr & =-\frac{m^{4}_{e}c^{5}}{\hbar ^{3}}y^{3}\left[ \frac{1}{10\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{1/3}\alpha Z^{2/3}y+\frac{18}{175\pi ^{2}}\left( \frac{4}{9\pi }\right) ^{2/3}\alpha ^{2}Z^{4/3}\frac{y^{2}}{\sqrt{1+y^{2}}}-\frac{0.031}{9\pi ^{2}}\alpha ^{2}+\frac{\alpha }{4\pi ^{3}}\frac{\chi \left( y\right) }{y^{3}}\right]\,, \cr } \end{displaymath} (4.30)

gde

\begin{displaymath} \hbox{% \begin{tabular}{l} $\displaystyle{ \chi \left( y\right) =\frac{y^{4}}{3}\frac{d}{dy}\left[ y\varphi \left( y\right) \right] =\frac{1}{32}\left( \beta ^{4}+\frac{1}{\beta ^{4}}\right) +\frac{1}{4}\left( \beta ^{2}+\frac{1}{\beta ^{2}}\right) -\frac{9}{16}-\frac{3}{4}\left( \beta ^{2}-\frac{1}{\beta ^{2}}\right) \ln \beta +\frac{3}{2}\left( \ln \beta \right) ^{2}- }$ \\ $\displaystyle{ \qquad\qquad -\frac{y}{3}\left( 1+\frac{y}{\sqrt{1+y^{2}}}\right) \left[ \frac{1}{8}\left( \beta ^{2}-\frac{1}{\beta ^{5}}\right) -\frac{1}{4}\left( \beta -\frac{1}{\beta ^{3}}\right) -\frac{3}{2}\left( \beta +\frac{1}{\beta ^{3}}\right) \ln \beta +\frac{3}{\beta }\ln \beta \right] , }$ \\[3mm] $\displaystyle{ \chi \left( y\right) =\left\{ \begin{array}{cl} y^{4}/3 & \quad \mbox{pri~} y\ll 1 , \\ -y^{4}/6 & \quad \mbox{pri~} y\gg 1 . \\ \end{array}\right. }$ \\ \end{tabular}} \end{displaymath}

Otsyuda v predel'nyh sluchayah imeem s uchetom (2.32) i (2.33)

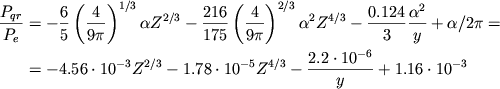\begin{displaymath} \eqalign{ \frac{P_{qr}}{P_{e}}& =-\frac{6}{5}\left( \frac{4}{9\pi }\right) ^{1/3}\alpha Z^{2/3}-\frac{216}{175}\left( \frac{4}{9\pi }\right) ^{2/3}\alpha ^{2}Z^{4/3}-\frac{0.124}{3}\frac{\alpha ^{2}}{y}+\alpha /2\pi = \cr & =-4.56\cdot 10^{-3}Z^{2/3}-1.78\cdot 10^{-5}Z^{4/3}-\frac{2.2\cdot 10^{-6}}{y}+1.16\cdot 10^{-3} \cr } \end{displaymath} (4.31)

dlya \( y\gg 1 \) [555].


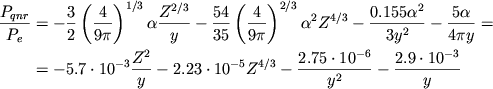\begin{displaymath} \eqalign{ \frac{P_{qnr}}{P_{e}}& =-\frac{3}{2}\left( \frac{4}{9\pi }\right) ^{1/3}\alpha \frac{Z^{2/3}}{y}-\frac{54}{35}\left( \frac{4}{9\pi }\right) ^{2/3}\alpha ^{2}Z^{4/3}-\frac{0.155\alpha ^{2}}{3y^{2}}-\frac{5\alpha }{4\pi y}= \cr & =-5.7\cdot 10^{-3}\frac{Z^{2}}{y}-2.23\cdot 10^{-5}Z^{4/3}-\frac{2.75\cdot 10^{-6}}{y^{2}}-\frac{2.9\cdot 10^{-3}}{y} \cr } \end{displaymath} (4.32)

dlya \( y\ll 1 \). Formuly (4.30), (4.32) primenimy tol'ko dlya znachenii \( y \), pri kotoryh \( P_{q}/P_{e}\ll 1 \). S umen'sheniem plotnosti kulonovskoe vzaimodeistvie kachestvenno menyaet vid uravneniya sostoyaniya. V [647] privedeno priblizhennoe analiticheskoe sootnoshenie dlya uravneniya sostoyaniya:
\begin{displaymath} \rho =\rho _{0}(\zeta +\varphi )^{3} , \quad \zeta ^{5}\equiv P/P_{0} , \end{displaymath} (4.33)

gde
\begin{displaymath} \rho _{0}=\frac{32}{3}\pi ^{-3}AZm_{u}a_{0}^{-3}=3.88ZA\cdot \mbox{g}\cdot \mbox{sm}^{-3} , \end{displaymath} (4.34)


\begin{displaymath} P_{0}=Z^{10/3}\frac{2^{8}\left( 2\pi \right) ^{1/3}}{15\pi ^{4}}\left( \frac{e^{2}}{\hbar c}\right) ^{2}\frac{m_{e}c^{2}}{a_{0}^{3}}=9.52\cdot 10^{13}Z^{10/3} \mbox{din}\cdot \mbox{sm}^{-2} \end{displaymath}


\begin{displaymath} \varphi =\frac{1}{20}3^{1/3}+\frac{1}{8}\left( \frac{3}{4}\pi ^{-2}Z^{-2}\right) ^{1/3} , \quad a_{0}=\hbar ^{2}/m_{e}e^{2} . \end{displaymath}

pri \( \rho \gg \rho _{0} \), \( \zeta \gg \varphi \) uravnenie sostoyaniya (4.33) svoditsya k (39.3).

V silu kvantovyh svoistv veshestva iony v reshetke pri absolyutnom nule sovershayut kolebaniya s chastotoi, opredelyaemoi vzaimodeistviem s elektronami. V \( WS \) priblizhenii vozvrashayushaya sila, deistvuyushaya na ion so storony elektronov v yacheike pri otklonenii ot ravnovesiya, est'

\begin{displaymath} F\left( r\right) =-\frac{Zeq_{e}}{r^{2}}=\frac{4\pi }{3}Ze^{2}n_{e}r , \end{displaymath}

chto privodit k chastote garmonicheskih kolebanii [125, 555]
\begin{displaymath} \omega ^{2}_{i}=\frac{F(r)}{Am_{u}r}=\frac{4\pi }{3}\frac{Ze^{2}n_{e}}{Am_{u}}=\frac{4}{9\pi }\frac{Zy^{3}}{Am_{u}}\alpha \frac{m_{e}^{3}c^{4}}{\hbar ^{2}} . \end{displaymath} (4.35)

Nulevuyu energiyu trehmernogo oscilyatora \( E_{zp}=\frac{3}{2}\hbar \omega _{i} \) sleduet sravnivat' s \( E_{c} \) iz (4.26). Imeem
\begin{displaymath} f=\frac{E_{zp}}{E_{c}}=\frac{5}{3}\left( \frac{4}{9\pi }\right) ^{1/6}\left( \frac{m_{e}}{m_{u}}\right) ^{1/2}\left( \frac{y}{\alpha AZ^{7/3}}\right) ^{1/2}=\left( 0.11\frac{y}{AZ^{7/3}}\right) ^{1/2} . \end{displaymath} (4.36)

Pri \( f\geq 1 \) kulonovskii kristall razrushaetsya uzhe pri nulevoi temperature za schet kvantovyh kolebanii. Pri etom neobhodimy slishkom bol'shie plotnosti \( \rho \gt 7.5\cdot 10^{8}\mu _{Z}A^{3}Z^{7} \), tak chto v holodnyh zvezdah nulevye kolebaniya ne razrushayut kristallicheskoi struktury.

Bolee real'nym yavlyaetsya razrushenie kristalla teplovymi dvizheniyami ionov [485, 620]. Plavlenie kristalla proishodit pri \( T=T_{m} \), kogda kineticheskaya energiya kolebanii \( kT \) sostavlyaet ~ 1/150 ot kulonovskoi energii \( WS \) yacheiki [544, 245,  578]11. Imeem s uchetom (4.26)

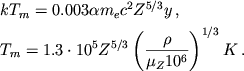\begin{displaymath} \eqalign{ & kT_{m}=0.003\alpha m_{e}c^{2}Z^{5/3}y\,, \cr & T_{m}=1.3\cdot 10^{5}Z^{5/3}\left( \frac{\rho }{\mu _{Z}10^{6}}\right) ^{1/3}K\,. \cr } \end{displaymath} (4.37)

Termodinamicheskie svoistva kristallicheskih tel horosho izvestny [145]. Pri malyh temperaturah vozbuzhdayutsya tol'ko stepeni svobody, sootvetstvuyushie dlinnym volnam (malym chastotam). Eti mody kolebanii (fonony) obladayut svoistvami, analogichnymi fotonnomu gazu. Naprotiv, pri bol'shih temperaturah vozbuzhdayutsya vse vozmozhnye mody kolebanii. Pri etom energiya kolebanii kristalla v dva raza bol'she kineticheskoi energii veshestva v gazovom sostoyanii pri toi zhe temperature. V obshem sluchae dlya teplovoi energii ionnoi reshetki na edinicu massy spravedliva interpolyacionnaya formula Debaya [145]

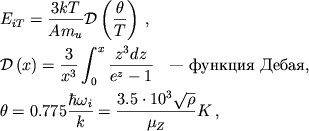\begin{displaymath} \eqalign{ & E_{iT}=\frac{3kT}{Am_{u}}{\cal D}\left( \frac{\theta }{T}\right)\,, \cr & {\cal D}\left( x\right) =\frac{3}{x^{3}}\int _{0}^{x}\frac{z^{3}dz}{e^{z}-1} \quad \mbox{--- funkciya Debaya,} \cr & \theta =0.775\frac{\hbar \omega _{i}}{k}=\frac{3.5\cdot 10^{3}\sqrt{\rho }}{\mu _{Z}}K\,, \cr } \end{displaymath} (4.38)

\( \theta \) - debaevskaya temperatura kulonovskoi reshetki [145, 620]. Zdes' \( \omega _{i} \) - chastota ionnyh kolebanii v kristalle (4.35). V predel'nyh sluchayah funkciya \( {\cal D}\left( x\right) \) ravna [145]12
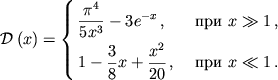\begin{displaymath} {\cal D}\left( x\right) =\left\{ \eqalignleft{ \frac{\pi ^{4}}{5x^{3}}-3e^{-x}\,, \quad & \mbox{~pri~} x\gg 1\,, \cr 1-\frac{3}{8}x+\frac{x^{2}}{20}\,, \quad & \mbox{~pri~} x\ll 1\,. \cr }\right. \end{displaymath} (4.39)

Entropiya edinicy massy i davlenie, svyazannye s ionnym kristallom, ravny [145]

\begin{displaymath} S_{iT}=\frac{k}{Am_{u}}\left[ -3\ln \left( 1-e^{-\frac{\theta }{T}}\right) +4{\cal D}\left( \frac{\theta }{T}\right) \right] , \end{displaymath}


\begin{displaymath} P_{iT}=\frac{3}{2}\frac{\rho kT}{Am_{u}}{\cal D}\left( \frac{\theta }{T}\right) =\frac{\rho E_{iT}}{2} . \end{displaymath} (4.40)

V predel'nyh sluchayah
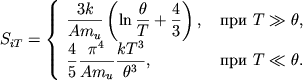\begin{displaymath} S_{iT}=\left\{ \begin{array}{ll} \displaystyle{ \frac{3k}{Am_{u}}\left( \ln \frac{\theta }{T}+\frac{4}{3}\right) , } & \mbox{~pri~} T\gg \theta , \\ \displaystyle{ \frac{4}{5}\frac{\pi ^{4}}{Am_{u}}\frac{kT^{3}}{\theta ^{3}} , } & \mbox{~pri~} T\ll \theta . \\ \end{array}\right. \end{displaymath} (4.41)

V zavisimosti ot sootnosheniya mezhdu temperaturami \( T \), \( T_{m} \) i \( \theta \) imeem sleduyushie sostoyaniya ionizovannogo veshestva:

\( T\lt \theta \lt T_{m} \) \( \theta \lt T\lt T_{m} \) \( \theta \lt T_{m}\lt T \) \( T_{m}\lt \theta \lt T \) \( T\lt T_{m}\lt \theta \) \( T_{m}\lt T\lt \theta \)
Kvantovyi (vyrozhdennyi) kristall Klassicheskii ionnyi kristall Klassicheskaya zhidkost' (neideal'naya plazma) Kvantovaya zhidkost'

Plavlenie ionnogo kristalla pri \( T\gt T_{m}\gt \theta \) soprovozhdaetsya vydeleniem tepla, a pri dal'neishem roste temperatury proishodit perehod k ideal'nomu gazu s \( E_{iT}=\frac{3}{2}kT/Am_{u} \). Soglasno [544, 245, 578] priblizhenie ideal'nogo gaza stanovitsya primenimym pri:

\begin{displaymath} T_{g}\approx 150T_{m}\approx 2\cdot 10^{7}Z^{5/3}\left( \rho /\mu _{Z}10^{6}\right) ^{1/3}K . \end{displaymath} (4.42)

V promezhutke \( T_{m}\lt T\lt 150T_{m} \) mozhno ispol'zovat' interpolyaciyu. Vopros o teplote plavleniya ne vpolne yasen. V [485] privodyatsya argumenty v pol'zu ochen' maloi teploty plavleniya pri postoyannyh \( T \) i \( \rho \). V [620] iz drugih soobrazhenii predpolagaetsya, chto fazovyi perehod otnositsya k pervomu rodu i teplota plavleniya reshetki pri postoyannyh \( T \) i \( \rho \) est'

\begin{displaymath} \delta U_{coul}\approx -\frac{3}{4}kT_{m} . \end{displaymath} (4.43)

Strogogo resheniya etoi problemy ne sdelano.

Naibolee slozhen dlya kolichestvennogo opisaniya promezhutochnyi interval plotnostei \( \rho _{i1}\lt \rho \lt \rho _{i2} \), gde stepen' ionizacii opredelyaetsya kak teplovoi energiei, tak i davleniem. V TF priblizhenii process ionizacii holodnogo veshestva davleniem issledovan v [126]. Obolochechnye popravki privodyat k skachkam davleniya pri kazhdoi posleduyushei ionizacii, pri plotnosti

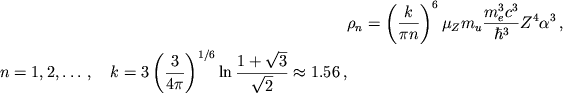\begin{displaymath} \eqalign{ & \rho _{n}=\left( \frac{k}{\pi n}\right) ^{6}\mu _{Z}m_{u}\frac{m^{3}_{e}c^{3}}{\hbar ^{3}}Z^{4}\alpha ^{3}\,, \cr n=1,2,\ldots\,, \quad k=3\left( \frac{3}{4\pi }\right) ^{1/6}\ln \frac{1+\sqrt{3}}{\sqrt{2}}\approx 1.56\,, \cr } \end{displaymath} (4.44)

Zavisimost' nemonotonnoi popravki k davleniyu ot plotnosti zadaetsya formuloi [126]

\begin{displaymath} \delta P=-12\left( \frac{9\pi }{4}\right) ^{1/6}k\frac{Z^{5/3}\upsilon ^{4/3}}{\ln \left( Z^{3}\upsilon \right) }\left[ S_{0}\right] \frac{m^{4}_{e}c^{5}}{\hbar ^{3}}\alpha ^{5} , \end{displaymath} (4.45)

gde
\begin{displaymath} \upsilon =\frac{Am_{u}}{\rho }\alpha \frac{m^{3}_{e}c^{4}}{\hbar ^{3}} , \quad S_{0}=kZ^{1/2}\upsilon ^{1/6}-\pi /2 , \end{displaymath} (4.46)

\( \left[ f\left( S_{0}\right) \right] \) pri \( -\pi /2\lt S_{0}\lt \frac{\pi }{2} \) s periodicheskim prodolzheniem vne etoi oblasti. Skachki davleniya (4.45), voznikayushie pri \( \rho =\rho _{n} \) i \( \upsilon =\upsilon _{n} \), sootvetstvuyut fazovym perehodam pervogo roda. V okrestnosti \( \rho =\rho _{n} \) davlenie elektronov postoyanno, prichem velichina \( P_{n} \) nahoditsya po pravilu Maksvella (ravenstvo ploshadei, ris. 14). Obolochechnye effekty ischezayut, soglasno (4.44), pri
\begin{displaymath} \rho \gt \rho _{1}=0.015\mu _{Z}m_{u}\frac{m^{3}_{e}c^{3}}{\hbar ^{3}}\alpha ^{3}Z^{4} , \end{displaymath} (4.47)

kogda vse urovni energii uhodyat v nepreryvnyi spektr. Po fizicheskomu smyslu \( \rho \leq \rho _{i2} \) iz (4.24). Esli prinyat', chto pri \( \rho =\rho _{i2} \) elektrony stanovyatsya relyativistskimi s \( y=1 \), to poluchaem \( \theta _{i2}=1.11 \) i uslovie \( Z\leq 49 \) dlya primenimosti nerelyativistskogo TF-rassmotreniya processa ionizacii [126].

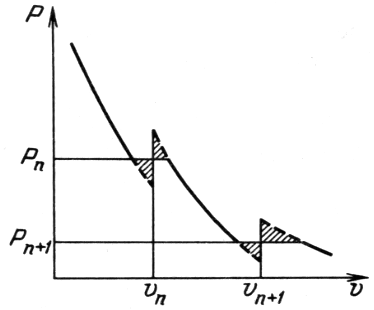Ris. 14. Shematicheskaya zavisimost' davleniya ot udel'nogo ob'ema pri uchete obolochechnyh effektov. Postoyannye urovni davleniya $R_n$ nahodyatsya iz ravenstva zashtrihovannyh ploshadei

Termodinamicheskie svoistva smesi vodoroda i geliya pri konechnoi temperature s uchetom vzaimodeistviya i ionizacii davleniem izuchalis' v [403]. Uchityvalis' soedineniya \( H_{2} \), \( H \), \( H^{+} \), \( H^{-} \), \( He \), \( He^{+} \), \( He^{++} \). Dlya dannoi temperatury \( T \) i polnogo chisla ionov \( N_{i} \) v ob'eme \( V \) vychislyaetsya svobodnaya energiya \( F \) v vide

\begin{displaymath} F=F_{0}+F_{c} , \end{displaymath} (4.48)

gde \( F_{0} \) sootvetstvuet ideal'nomu gazu, a \( F_{c} \) otrazhaet kulonovskoe vzaimodeistvie. Davlenie \( P \), entropiya \( S \) i energiya sistemy \( E \) nahodyatsya iz sootnoshenii
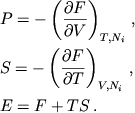\begin{displaymath} \eqalign{ & P=-\left( \frac{\partial F}{\partial V}\right) _{T,N_{i}}\,, \cr & S=-\left( \frac{\partial F}{\partial T}\right) _{V,N_{i}}\,, \cr & E=F+TS\,. \cr } \end{displaymath} (4.49)

Kulonovskoe vzaimodeistvie uchityvaetsya zdes' takzhe v vide popravok k ideal'nomu gazu

\begin{displaymath} P=P_{0}+P_{c}\,, \quad S=S_{0}+S_{c}\,, \quad E=E_{0}+E_{c}\,. \end{displaymath} (4.50)

Na osnove TF teorii s debai-h'yukkelevskim potencialom vokrug yadra (TFDH) imeem [403]

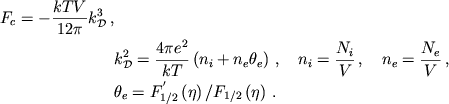\begin{displaymath} \eqalign{ F_{c}=-\frac{kTV}{12\pi }k_{{\cal D}}^{3}\,, \cr & k^{2}_{{\cal D}}=\frac{4\pi e^{2}}{kT}\left( n_{i}+n_{e}\theta _{e}\right)\,, \quad n_{i}=\frac{N_{i}}{V}\,, \quad n_{e}=\frac{N_{e}}{V}\,, \cr & \theta _{e}=F_{1/2}^{'}\left( \eta \right) /F_{1/2}\left( \eta \right)\,. \cr } \end{displaymath} (4.51)

gde \( F_{\alpha }(\eta ) \) - funkcii Fermi iz (2.49), \( \eta kT \) - himicheskii potencial svobodnyh elektronov, \( k^{-1}_{{\cal D}} \) - debaevskii radius (sm. takzhe (8.47)), i predpolagaetsya, chto vse iony imeyut odinakovyi srednii zaryad \( Z=1 \). Dlya rassmotrennoi smesi s \( x_{H}=0.739 \), \( x_{He}=0.261 \) velichina \( Z \) menyaetsya ot edinicy do 1.0811 pri izmenenii sostava ot polnost'yu neitral'nogo do polnost'yu ionizovannogo, \( n_{e} \) - koncentraciya svobodnyh elektronov. S uchetom (4.51), popravki k termodinamicheskim funkciyam ravny
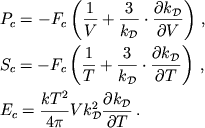\begin{displaymath} \eqalign{ & P_{c}=-F_{c}\left( \frac{1}{V}+\frac{3}{k_{\cal D}}\cdot \frac{\partial k_{\cal D}}{\partial V}\right)\,, \cr & S_{c}=-F_{c}\left( \frac{1}{T}+\frac{3}{k_{\cal D}}\cdot \frac{\partial k_{\cal D}}{\partial T}\right)\,, \cr & E_{c}=\frac{kT^{2}}{4\pi }Vk^{2}_{\cal D}\frac{\partial k_{\cal D}}{\partial T}\,. \cr } \end{displaymath} (4.52)

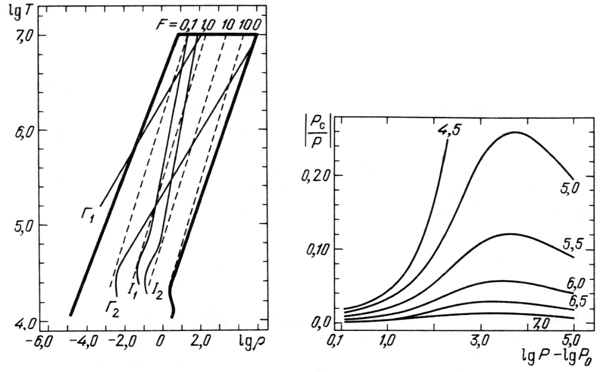
Rezul'taty TFDH rassmotreniya verny pri

\begin{displaymath} \Gamma_{e}=\frac{e^{2}}{kT}\left( \frac{4\pi }{3}n_{e}\right) ^{1/3}\ll 1 . \end{displaymath} (4.53)

V [403] TFDH teoriya primenyaetsya pri \( \Gamma_{e}\lt 0.1 \), pri \( \Gamma_{e}\gt 1 \) ispol'zuyutsya rezul'taty raschetov Monte-Karlo, a pri \( 0.1\lt \Gamma_{e}\lt 1 \) rezul'taty oboih metodov interpoliruyutsya.

Dlya opredeleniya stepeni ionizacii ispol'zuetsya uravnenie Saha, v kotorom uchityvaetsya, v dopolnenie k (1.8), konechnaya stepen' vyrozhdeniya svobodnyh elektronov, vliyayushaya na ih himicheskii potencial. Sdvig urovnei ionov i molekul pri uchete ekraniruyushego DH potenciala privodit k umen'sheniyu chisla svyazannyh sostoyanii i umen'shenii ih glubiny. Ih uchet v formule Saha otrazhaet ionizaciyu davleniem. V celom, uchet ionizacii davleniem svoditsya k slozhnoi samosoglasovannoi probleme, v kotoroi koncentraciya svobodnyh elektronov pe i ionov i,- opredelyaet DH radius i potencial, a te, v svoyu ochered', opredelyayut koncentraciyu posredstvom sdviga urovnei, vhodyashih v uravnenie Saha. Zadacha oslozhnyaetsya otsutstviem analiticheskih reshenii dlya uravneniya Shredingera s DH potencialom [240], poetomu neobhodimy chislennye raschety. Rezul'taty takih raschetov, vypolnennyh v [403], predstavleny na ris. 15 i 16. Tablicy uravneniya sostoyaniya s uchetom kulonovskogo vzaimodeistviya, rasschitannye analogichnym sposobom, dany v [358].

Ris. 15. Oblast' na ploskosti $(\lg\rho, \lg T)$, gde rasschityvalis' termodinamicheskie funkcii [403]. Sleva ot linii $\Gamma_e = \Gamma_1$ = 0,1 raschety velis' po TFDH teorii, sprava ot linii $\Gamma_e = \Gamma_1$ = 1,0 po metodu Monte-Karlo (sm. (4.53)). Sleva ot linii $I_1$ vodorod i gelii chastichno ionizovany, mezhdu liniyami $I_1$ i $I_2$ vodorod ionizovan polnost'yu, a gelii chastichno, a sprava ot linii $I_2$ oba ionizovany polnost'yu, shtrihami ukazany linii postoyannogo znacheniya $F = 4F_{1/2}(\eta)/\sqrt{\pi\,}$, harakterizuyushie vyrozhdenie, v nevyrozhdennoi plazme $F \ll 1$.
Ris. 16. Otnoshenie kulonovskoi popravki k davleniyu k polnomu davleniyu pri T = const. Na kazhdoi krivoi ukazana velichina $\lg T$, dlya kotoroi $\lg P_0 = 2,74118$, $\lg T = 4,58825$

Zadacha. Sdelat' gladkuyu interpolyaciyu uravneniya sostoyaniya holodnogo veshestva neitronnyh zvezd.

Reshenie [14]. Gladkaya s pervoi proizvodnoi interpolyaciya uravneniya sostoyaniya \( P(\rho ) \) iz tabl. 9 [479] opredelyaetsya sleduyushimi formulami (\( \rho \) - polnaya plotnost' massy-energii s uchetom vzaimodeistviya):

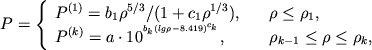\begin{displaymath} P=\left\{ \begin{array}{ll} \displaystyle{ P^{(1)}=b_{1}\rho ^{5/3}/(1+c_{1}\rho ^{1/3}) ,\quad } & \rho \leq \rho _{1} , \\ \displaystyle{ P^{(k)}=a\cdot 10^{^{b_{k}(lg\rho -8.419)^{c_{k}}}} ,\quad } &\rho _{k-1}\leq \rho \leq \rho _{k} , \\ \end{array}\right. \end{displaymath} (1)

\( k=2,3,\ldots 6 \),
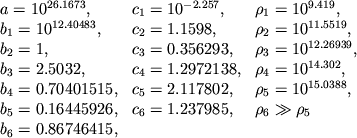
\(\displaystyle{ \begin{array}{@{}lll} a=10^{26.1673}, & c_{1}=10^{-2.257}, & \rho_{1}=10^{9.419}, \\ b_{1}=10^{12.40483}, & c_{2}=1.1598, & \rho_{2}=10^{11.5519}, \\ b_{2}=1, & c_{3}=0.356293, & \rho_{3}=10^{12.26939}, \\ b_{3}=2.5032, & c_{4}=1.2972138, & \rho_{4}=10^{14.302}, \\ b_{4}=0.70401515, & c_{5}=2.117802, & \rho_{5}=10^{15.0388}, \\ b_{5}=0.16445926, & c_{6}=1.237985, & \rho_{6} \gg \rho_{5} \\ b_{6}=0.86746415, \\ \end{array}}\)

Nepreryvnost' proizvodnyh \( dP/d\rho \) v tochkah \( \rho =\rho _{k} \) iz (1) dostigaetsya s pomosh'yu sglazhivaniya v vide

\begin{displaymath} P(\rho )=\left\{ \eqalign{ & P^{(k)},\quad \rho \in \left[ \rho _{k-1}+\xi _{k-1},\rho _{k}-\xi _{k}\right], \quad k=1,2,...6, \cr & \theta _{k}P^{(k)}+(1-\theta _{k})P^{(k+1)}, \quad \rho \in \left[ \rho _{k}-\xi _{k}\,,\right. \cr & \left.\rho _{k}+\xi _{k}\right]\,, \quad \rho _{0}+\xi _{0}=0\,, }\right. \end{displaymath} (2)

gde

\begin{displaymath} \theta _{k}=\theta _{k}(\rho )=\frac{1}{2}-\frac{1}{2}\sin\left( \frac{\pi }{2\xi _{k}}(\rho -\rho _{k})\right) , \end{displaymath}


\begin{displaymath} \xi _{k}=0.01\rho _{k} . \end{displaymath}


<< 3. Uravnenie sostoyaniya pri ... | Oglavlenie |

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - fizicheskie processy
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 2.6 [golosov: 87]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya