3.2. Ekvatorial'naya sistema koordinat
Napravlenie osi vrasheniya Zemli yavlyaetsya vtorym vybrannym napravleniem dlya nablyudatelya, nahodyashegosya na poverhnosti Zemli. S napravleniem osi vrasheniya Zemli svyazana vtoraya shiroko ispol'zuemaya v astronomii sistema koordinat -- ekvatorial'naya.
Dopustim poka, chto centr nebesnoi sfery sovpadaet s centrom mass Zemli. Esli prodolzhit' os' vrasheniya Zemli do peresecheniya s nebesnoi sferoi, to tochki peresecheniya nazyvayutsya polyusami mira, a sama os' -- os'yu mira.
V nastoyashee vremya severnyi polyus mira raspolagaetsya vblizi (na
rasstoyanii menee ![]() ) ot Polyarnoi zvezdy (
) ot Polyarnoi zvezdy (![]() Maloi
Medvedicy). Poetomu Polyarnaya zvezda prakticheski nepodvizhna. Esli
nablyudatel' nahoditsya v severnom polusharii Zemli i budet smotret'
na nee dlitel'noe vremya, to uvidit, chto ostal'nye zvezdy sovershayut
krugovoe dvizhenie vokrug Polyarnoi zvezdy. Kazhusheesya vrashenie
nebesnoi sfery otnositel'no Polyarnoi zvezdy (tochnee vokrug osi
mira) proishodit protiv chasovoi strelki i yavlyaetsya otrazheniem
vrasheniya Zemli. Esli vstat' licom po napravleniyu k Polyarnoi
zvezde i provesti bol'shoi krug cherez nee (tochnee cherez severnyi
polyus mira) i zenit, to peresechenie etogo kruga s ploskost'yu
gorizonta opredelit tochku severa.
Maloi
Medvedicy). Poetomu Polyarnaya zvezda prakticheski nepodvizhna. Esli
nablyudatel' nahoditsya v severnom polusharii Zemli i budet smotret'
na nee dlitel'noe vremya, to uvidit, chto ostal'nye zvezdy sovershayut
krugovoe dvizhenie vokrug Polyarnoi zvezdy. Kazhusheesya vrashenie
nebesnoi sfery otnositel'no Polyarnoi zvezdy (tochnee vokrug osi
mira) proishodit protiv chasovoi strelki i yavlyaetsya otrazheniem
vrasheniya Zemli. Esli vstat' licom po napravleniyu k Polyarnoi
zvezde i provesti bol'shoi krug cherez nee (tochnee cherez severnyi
polyus mira) i zenit, to peresechenie etogo kruga s ploskost'yu
gorizonta opredelit tochku severa.
V dal'neishem izlozhenii budem schitat', chto na nebesnuyu sferu my smotrim snaruzhi. Eto analogichno vzglyadu na globus Zemli. Koordinaty zvezd v ekvatorial'noi sisteme v etom sluchae opredelyayutsya analogichno shirote i dolgote na poverhnosti Zemli. Zametim, chto pri vzglyade na nebesnuyu sferu snaruzhi raspolozhenie zvezd zerkal'no otlichaetsya ot togo, chto vidit nablyudatel' s poverhnosti Zemli.
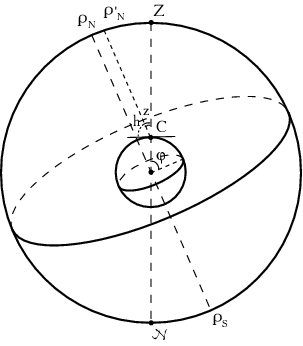
Otmetim na ris. 3.2 severnyi (![]() ) i yuzhnyi (
) i yuzhnyi (![]() ) polyusy
mira, a takzhe zenit
) polyusy
mira, a takzhe zenit ![]() i nadir
i nadir ![]() nablyudatelya, raspolozhennogo
v tochke
nablyudatelya, raspolozhennogo
v tochke ![]() na poverhnosti Zemli.
na poverhnosti Zemli.
Paradoks, sut' kotorogo zaklyuchaetsya v tom, chto s odnoi storony radius
nebesnoi sfery raven edinice, a s drugoi, chto tochki ![]() i
i ![]() raspolozheny na beskonechnom rasstoyanii, reshaetsya dostatochno prosto:
radius Zemli prenebrezhimo mal po sravneniyu s rasstoyaniem do blizhaishih
zvezd.
raspolozheny na beskonechnom rasstoyanii, reshaetsya dostatochno prosto:
radius Zemli prenebrezhimo mal po sravneniyu s rasstoyaniem do blizhaishih
zvezd.
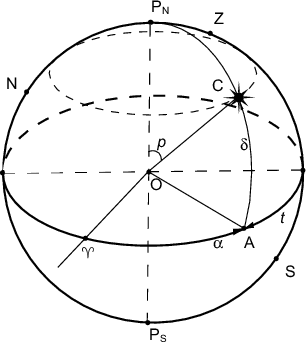
Pust' ![]() -- zvezda na nebesnoi sfere (ris. 3.3).
-- zvezda na nebesnoi sfere (ris. 3.3).
Vtoroi koordinatoi v ekvatorial'noi sisteme koordinat yavlyaetsya
pryamoe voshozhdenie ![]() .
Nikakogo osobogo (vydelennogo) napravleniya v ploskosti ekvatora
net. Poetomu vybor nachala otscheta pryamyh voshozhdenii proizvolen.
.
Nikakogo osobogo (vydelennogo) napravleniya v ploskosti ekvatora
net. Poetomu vybor nachala otscheta pryamyh voshozhdenii proizvolen.
Do 1998 goda eta tochka opredelyalas' v moment peresecheniya centrom Solnca nebesnogo ekvatora, kogda Solnce dvigaetsya iz yuzhnogo polushariya v severnoe. Eto proishodit primerno 21 marta kazhdogo goda, i tochka nazyvaetsya tochkoi vesennego ravnodenstviya. Protivopolozhnaya tochka na ekvatore nazyvaetsya tochkoi osennego ravnodenstviya. Etu tochku Solnce prohodit primerno 23 sentyabrya.
Vidimoe dvizhenie Solnca est' ne chto inoe, kak otrazhenie dvizheniya Zemli vokrug Solnca. Ploskost' zemnoi orbity nazovem ploskost'yu ekliptiki, kotoraya opredelyaet eklipticheskuyu sistemu koordinat. Poetomu, soglasno opredeleniyu, prinyatomu do 1998 g., tochki vesennego i osennego ravnodenstvii lezhali na linii peresecheniya nebesnogo ekvatora i ekliptiki. Tak kak koordinaty Zemli i Solnca nahodyatsya na osnove resheniya uravnenii dinamiki, to ploskost' ekliptiki opredelyaetsya na osnove dinamicheskogo metoda. Tochki vesennego i osennego ravnodenstvii, opredelyaemye peresecheniem ekvatora i ekliptiki, nazyvayutsya dinamicheskimi, a sam moment peresecheniya centrom Solnca dinamicheskoi tochki vesennego ravnodenstviya -- dinamicheskim ravnodenstviem.
S 1998 g. Mezhdunarodnym astronomicheskim soyuzom (MAS) v kachestve
realizacii nebesnoi sistemy koordinat prinyat katalog
vnegalakticheskih radioistochnikov. MAS rekomenduet, chtoby nachalo
pryamyh voshozhdenii novoi nebesnoi sistemy koordinat bylo blizkim
k dinamicheskomu ravnodenstviyu J2000.03.4. Dlya etogo nachalo sistemy otscheta pryamyh
voshozhdenii s 1998 g. po resheniyu MAS bylo opredeleno sleduyushim
obrazom. Iz raznyh katalogov byli vybrany 23 radioistochnika,
sredi kotoryh byl i kvazar 3C273, i vychisleny srednie znacheniya
pryamogo voshozhdeniya kazhdogo iz nih. Zatem koordinaty istochnikov
byli ispravleny takim obrazom, chtoby pryamoe voshozhdenie kvazara
3C273 bylo soglasovano so znacheniem v sisteme fundamental'nogo
kataloga FK5 (
![]() J2000.0), t.e.
raznica mezhdu etim znacheniem i srednim pryamym voshozhdeniem
3C273 byla dobavlena k pryamym voshozhdeniyam ostal'nyh 22
istochnikov. Pri takom opredelenii tochka vesennego ravnodenstviya
uzhe ne privyazyvaetsya k ekliptike.
J2000.0), t.e.
raznica mezhdu etim znacheniem i srednim pryamym voshozhdeniem
3C273 byla dobavlena k pryamym voshozhdeniyam ostal'nyh 22
istochnikov. Pri takom opredelenii tochka vesennego ravnodenstviya
uzhe ne privyazyvaetsya k ekliptike.
V nastoyashee vremya tochka vesennego ravnodenstviya nahoditsya v
sozvezdii Ryb, tochka osennego ravnodenstviya -- v sozvezdii Devy.
Prinyatoe oboznachenie tochek -- ![]() i
i ![]() dlya vesennego
i osennego ravnodenstvii, sootvetstvenno, otnosyatsya k znakam Ovna
i Vesov. Prichinoi smesheniya tochek vesennego i osennego
ravnodenstviya yavlyaetsya precessiya, o kotoroi my rasskazhem
pozzhe. V rezul'tate precessii ploskost'
nebesnogo ekvatora ne sohranyaet svoe polozhenie v prostranstve, a
polyusy mira opisyvayut na nebesnoi sfere okruzhnost' priblizitel'no
za 26000 let. Primerno 4500 let nazad severnyi polyus mira
nahodilsya okolo zvezdy
dlya vesennego
i osennego ravnodenstvii, sootvetstvenno, otnosyatsya k znakam Ovna
i Vesov. Prichinoi smesheniya tochek vesennego i osennego
ravnodenstviya yavlyaetsya precessiya, o kotoroi my rasskazhem
pozzhe. V rezul'tate precessii ploskost'
nebesnogo ekvatora ne sohranyaet svoe polozhenie v prostranstve, a
polyusy mira opisyvayut na nebesnoi sfere okruzhnost' priblizitel'no
za 26000 let. Primerno 4500 let nazad severnyi polyus mira
nahodilsya okolo zvezdy ![]() Drakona (Tuban), kotoraya byla v
to vremya polyarnoi. Cherez 2000 let polyarnoi budet zvezda
Drakona (Tuban), kotoraya byla v
to vremya polyarnoi. Cherez 2000 let polyarnoi budet zvezda ![]() Cefeya (Al'ran), a cherez 14000 let -- Vega (sozvezdie Lira).
Cefeya (Al'ran), a cherez 14000 let -- Vega (sozvezdie Lira).
Esli pri vychislenii polozheniya nebesnogo ekvatora na opredelennyi moment vremeni uchityvaetsya tol'ko yavlenie precessii (nutaciya ne prinimaetsya vo vnimanie), to ekvator nazyvaetsya srednim. Mezhdunarodnyi astronomicheskii soyuz rekomenduet otnosit' koordinaty zvezd ili radioistochnikov k srednemu ekvatoru dlya vybrannyh momentov vremeni, tak nazyvaemym standartnym epoham. V nastoyashee vremya standartnoi epohoi schitaetsya data: yanvar' 1,5 2000 g. Moment vremeni opredelyaetsya dlya geocentricheskoi sistemy otscheta v shkale zemnogo vremeni (Terrestrial Time, TT) (sm. §5.5.2).
Esli tochka vesennego ravnodenstviya ![]() opredelena, to duga
ekvatora
opredelena, to duga
ekvatora
![]() ot tochki vesennego ravnodenstviya do
kruga sklonenii zvezdy nazyvaetsya pryamym
voshozhdeniem:
ot tochki vesennego ravnodenstviya do
kruga sklonenii zvezdy nazyvaetsya pryamym
voshozhdeniem:
Esli ![]() -- zenit nablyudatelya,
-- zenit nablyudatelya, ![]() i
i ![]() -- tochki severa i yuga na ploskosti gorizonta (na ris. 3.3
gorizont ne pokazan), to, kak bylo skazano ran'she, ploskost'
-- tochki severa i yuga na ploskosti gorizonta (na ris. 3.3
gorizont ne pokazan), to, kak bylo skazano ran'she, ploskost'
![]() yavlyaetsya ploskost'yu nebesnogo meridiana. Dvugrannyi
ugol mezhdu ploskost'yu nebesnogo meridiana i krugom skloneniya
nazyvaetsya chasovym uglom
yavlyaetsya ploskost'yu nebesnogo meridiana. Dvugrannyi
ugol mezhdu ploskost'yu nebesnogo meridiana i krugom skloneniya
nazyvaetsya chasovym uglom ![]() svetila.
Chasovye ugly otschityvayutsya ot vysshei tochki ekvatora po chasovoi
strelke, esli smotret' s severnogo polyusa mira, ot
svetila.
Chasovye ugly otschityvayutsya ot vysshei tochki ekvatora po chasovoi
strelke, esli smotret' s severnogo polyusa mira, ot ![]() do
do
![]() ili ot
ili ot ![]() do
do ![]() . Zametim, chto sistema
koordinat
. Zametim, chto sistema
koordinat
![]() , zadavaemaya chasovym uglom i skloneniem,
yavlyaetsya levoi.
, zadavaemaya chasovym uglom i skloneniem,
yavlyaetsya levoi.
Malyi krug, parallel'nyi ekvatoru i prohodyashii cherez zvezdu ![]() ,
nazyvaetsya parallel'yu (pokazan punktirnoi liniei na
ris. 3.3).
,
nazyvaetsya parallel'yu (pokazan punktirnoi liniei na
ris. 3.3).
V ekvatorial'noi sisteme koordinat osnovnymi krugami yavlyayutsya: ekvator, ot kotorogo otschityvayutsya skloneniya, nebesnyi meridian, krug sklonenii. Osnovnye tochki -- eto polyusy mira, tochka vesennego ravnodenstviya -- nachalo otscheta pryamyh voshozhdenii -- i vysshaya tochka ekvatora -- nachalo otscheta chasovyh uglov.
Bazisnuyu troiku vektorov, opredelyayushih ekvatorial'nuyu sistemu
koordinat, oboznachim kak
![]() , prichem vektor
, prichem vektor
![]() napravlen v severnyi polyus mira
napravlen v severnyi polyus mira ![]() i opredelyaet os'
i opredelyaet os'
![]() dekartovoi sistemy koordinat, vektor
dekartovoi sistemy koordinat, vektor ![]() napravlen v
tochku vesennego ravnodenstviya
napravlen v
tochku vesennego ravnodenstviya ![]() i opredelyaet os'
i opredelyaet os' ![]() , a
vektor
, a
vektor ![]() raven:
raven:
![]() i zadaet
os'
i zadaet
os' ![]() , tak chto
, tak chto
![]() sostavlyayut pravuyu
troiku vektorov.
sostavlyayut pravuyu
troiku vektorov.
<< 3.1. Gorizontal'naya sistema koordinat | Oglavlenie | 3.3. Eklipticheskaya sistema koordinat >>
|
Publikacii s klyuchevymi slovami:
astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |