Astronet > Sfericheskaya astronomiya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 3.2. Ekvatorial'naya sistema koordinat | Oglavlenie | 3.4. Galakticheskaya sistema koordinat >>

3.3. Eklipticheskaya sistema koordinat

Pri izuchenii dvizheniya tel solnechnoi sistemy udobnee ispol'zovat' ne ekvatorial'nuyu, a eklipticheskuyu sistemu koordinat. Delo v tom, chto ploskosti orbit bol'shinstva tel solnechnoi sistemy nakloneny k ploskosti orbity Zemli pod malymi uglami (iz planet samyi bol'shoi naklon u orbity Plutona -- $\sim 17^\circ$ ). Poetomu dlya nablyudatelya, nahodyashegosya na Zemle, vybor v kachestve osnovnoi ploskosti sistemy ploskosti orbity Zemli vpolne estestvenen.

Osnovoi dlya postroeniya eklipticheskoi sistemy koordinat sluzhit uravneniya dinamiki, opisyvayushie dvizhenie Zemli po orbite vokrug Solnca. Srednyaya ploskost' orbity Zemli nazyvaetsya ploskost'yu ekliptiki, a peresechenie etoi ploskost'yu nebesnoi sfery -- ekliptikoi. Dvizhenie Zemli po orbite privodit k kazhushemusya dvizheniyu Solnca po otnosheniyu k dalekim zvezdam. Polnyi oborot po ekliptike Solnce prohodit za god. Znachit, Solnce dvizhetsya otnositel'no zvezd so skorost'yu $\sim 1^\circ$ v sutki.

Os' vrasheniya Zemli naklonena k ploskosti orbity pod uglom $\sim 23\hbox{$^{\circ}$\kern-.15cm{,}\kern.04cm}5$ . Ochevidno, chto ugol $\varepsilon$ mezhdu ploskostyami ekvatora i ekliptiki (nazovem ego naklonom ekliptiki k ekvatoru) takzhe raven etoi velichine. Ugol $\varepsilon$ medlenno menyaetsya iz-za precessii ot planet. Prityazhenie planetami Zemli privodit takzhe k vozmusheniyam v dvizhenii Zemli. V rezul'tate centr mass Zemli okazyvaetsya to nizhe, to vyshe srednei ploskosti orbity Zemli. Kak otrazhenie vozmushenii v dvizhenii Zemli my vidim, chto centr Solnca nahoditsya to vyshe, to nizhe ekliptiki.

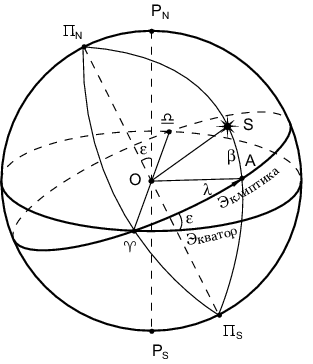
Glavnoi ploskost'yu v eklipticheskoi sisteme koordinat yavlyaetsya ploskost' ekliptiki. Severnyi polyus ekliptiki oboznachim cherez $\Pi_N$ ; po opredeleniyu duga $\widehat{P_N\Pi_N}$ dolzhna byt' men'she $90^\circ$ (ris. 3.4).

Ris. 3.4. Eklipticheskaya sistema koordinat

Yuzhnyi polyus ekliptiki oboznachim kak $\Pi_S$ . Liniya peresecheniya dvuh ploskostei -- nebesnogo ekvatora i ekliptiki nazyvaetsya liniei uzlov. Ekliptika delit nebesnuyu sferu na dva polushariya: severnoe i yuzhnoe.

Opredelenie 3.3.1 Bol'shoi krug, provedennyi cherez polyusy ekliptiki i nebesnyi ob'ekt, nazyvaetsya krugom shiroty.

Duga kruga shiroty $\widehat{AS}$ , otschityvaemaya ot ploskosti ekliptiki, nazyvaetsya eklipticheskoi shirotoi :

$\displaystyle \widehat{AS}=\beta.$

Shirota polozhitel'na v severnom i otricatel'na v yuzhnom polusharii: $-90^\circ\le \beta \le 90^\circ$ .

Vtoroi koordinatoi yavlyaetsya eklipticheskaya dolgota, ravnaya dvugrannomu uglu mezhdu bol'shim krugom, kotoryi prohodit cherez polyusy ekliptiki i dinamicheskuyu tochku vesennego ravnodenstviya, i krugom shiroty:

$\displaystyle \widehat{\aries A}=\lambda.$

Dolgota izmeryaetsya ot tochki vesennego ravnodenstviya ot $0^\circ$ do $360^\circ$ protiv chasovoi strelki, esli smotret' s severnogo polyusa ekliptiki, to est' v napravlenii vozrastaniya pryamyh voshozhdenii. Os' $Ox$ v eklipticheskoi sisteme koordinat sovpadaet s os'yu $Ox$ ekvatorial'noi sistemy. Oboznachim orty eklipticheskoi sistemy cherez ${\bf i}_e, {\bf j}_e,{\bf k}_e$ , prichem ${\bf i}_e={\bf i}$ , vektor ${\bf k}_e$ napravlen v severnyi polyus ekliptiki $\Pi_N$ , a ${\bf j}_e={\bf k}_e\times {\bf i}_e$ .

Osnovnymi krugami v eklipticheskoi sisteme koordinat yavlyayutsya ekliptika, krug shiroty, a osnovnymi tochkami -- polyusy ekliptiki i tochka vesennego ravnodenstviya.

<< 3.2. Ekvatorial'naya sistema koordinat | Oglavlenie | 3.4. Galakticheskaya sistema koordinat >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni

Sm. takzhe:

Dostizheniya kosmicheskoi astrometrii

Skonchalsya Konstantin Vladislavovich Kuimov

Konstantinu Vladislavovichu Kuimovu – 75 let

Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya.

Vrashenie Zemli i prodolzhitel'nost' sutok

80 let so dnya rozhdeniya Al'berta Petrovicha Gulyaeva

Rukovodstvo po prakticheskoi rabote s katalogom Hipparcos

Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce