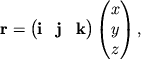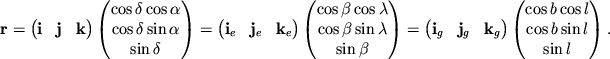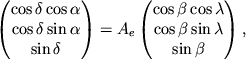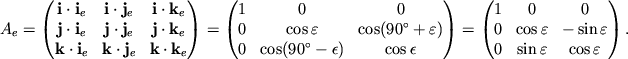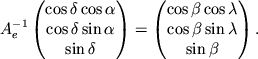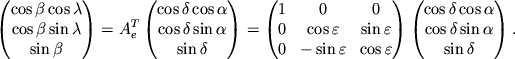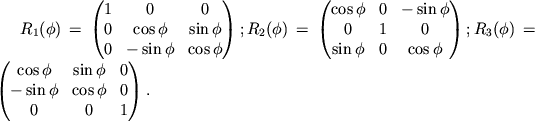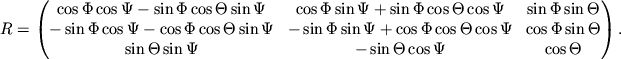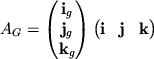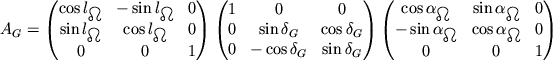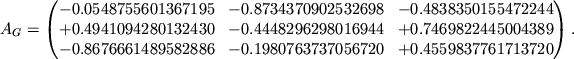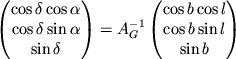Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu << 3.4. Galakticheskaya sistema koordinat | Oglavlenie | 3.6. Sutochnoe vrashenie nebesnoi >>

3.5. Preobrazovanie koordinat iz odnoi sistemy v druguyu

Dannaya zadacha uzhe upominalas' pri rassmotrenii gorizontal'noi sistemy koordinat. Esli sistema ustanovki teleskopa gorizontal'naya, to dvizhenie zvezd v etoi sisteme budet neravnomernym. Dlya tochnogo vedeniya teleskopa za zvezdoi trebuetsya nepreryvno pereschityvat' ekvatorial'nye koordinaty zvezdy v gorizontal'nye.

Rassmotrim snachala klassicheskii metod i naidem vyrazheniya, svyazyvayushie ekvatorial'nye i gorizontal'nye koordinaty. Zatem rassmotrim matrichnyi metod, kotoryi znachitel'no oblegchaet zadachu preobrazovaniya koordinat vektora iz odnoi sistemy v druguyu.

Rassmotrim treugol'nik $ {P_N}ZC$ (ris. 3.6).

Ris. 3.6. Svyaz' gorizontal'nyh i ekvatorial'nyh koordinat

Vershinami v etom treugol'nike yavlyayutsya zenit, polyus mira i zvezda $ C$. Takoi treugol'nik nazyvaetsya parallakticheskim. Soglasno opredeleniyam koordinat, imeem: duga $ \widehat{ZC}$ ravna zenitnomu rasstoyaniyu $ z$, duga $ \widehat{P_NC}$ ravna $ 90^\circ-\delta$, duga $ \widehat {P_NZ}$ ravna $ 90^\circ-\varphi$, dvugrannyi ugol $ Z{P_N}C$ -- eto chasovoi ugol $ t$, dvugrannyi ugol $ {P_N}ZC$ raven $ 180^\circ-A$. Dopustim, chto trebuetsya naiti zenitnoe rasstoyanie i azimut istochnika po ego sfericheskim koordinatam. Po teoreme kosinusov, ispol'zuya treugol'nik $ {P_N}ZC$, imeem:

$\displaystyle \cos{z}=\cos(90^\circ-\delta) \cos(90^\circ-\varphi) +\sin(90^\circ-\delta) \sin(90^\circ-\varphi) \cos{t} $

ili

$\displaystyle \cos{z}=\sin{\delta} \sin{\varphi} +\cos{\delta} \cos{\varphi} \cos{t}$ (3.1)

Po teoreme sinusov poluchim:

$\displaystyle \frac{\sin{z}}{\sin{t}}=\frac{\sin(90^\circ-\delta)}{\sin(180^\circ-A)} $

ili

$\displaystyle \sin{z} \sin{A} =\cos{\delta} \sin{t}$ (3.2)

Po teoreme podobiya poluchim:

$\displaystyle \sin z \cos (180^\circ -A) = \cos (90^\circ -\delta) \sin (90^\circ -\varphi) - \sin (90^\circ -\delta) \cos (90^\circ-\varphi) \cos t $

ili

$\displaystyle \sin z \cos A = -\sin \delta \cos \varphi + \cos \delta \sin \varphi \cos t.$ (3.3)

Iz sistemy uravnenii (3.1-3.3) mozhno odnoznachno opredelit' $ z$ i $ A$ po koordinatam $ \delta$ i $ t$. Obratim vnimanie na neobhodimost' ispol'zovaniya vseh treh uravnenii (3.1-3.3) dlya resheniya zadachi. Tak kak azimut $ A$ vhodit v uravneniya pod znakom sinusa i kosinusa, to tol'ko sovmestnoe reshenie uravnenii (3.2-3.3) pozvolyaet odnoznachno naiti $ A$.

Obratnoe preobrazovanie (ot $ z$ i $ A$ k $ \delta$ i $ t$) mozhno zapisat' v vide:

$\displaystyle \cos \delta \cos t$ $\displaystyle =$ $\displaystyle \cos z \cos \varphi + \sin z \sin \varphi \cos A, \notag$ (4)
$\displaystyle \cos \delta \sin t$ $\displaystyle =$ $\displaystyle \sin z \sin A,$ (5)
$\displaystyle \sin \delta$ $\displaystyle =$ $\displaystyle \cos z \sin \varphi - \sin z \cos \varphi \cos A. \notag$ (6)

Tochno tak zhe mozhno poluchit' formuly, svyazyvayushie ekvatorial'nuyu sistemu koordinat s eklipticheskoi, ekvatorial'nuyu s galakticheskoi i t.d.

Odnako bolee prosto naiti preobrazovanie ot odnoi sistemy koordinat k drugoi sisteme s pomosh'yu matrichnyh metodov. Tak kak v dal'neishem my budem ispol'zovat' eti metody chasto, rassmotrim ih podrobno.

Razlozhenie vektora po troike bazisnyh vektorov ($ \bf i$, $ \bf j$, $ \bf k$) bylo zapisano v vide (2.5):

$\displaystyle {\bf r} = x{\bf i} + y{\bf j} + z{\bf k}, $

gde $ x$, $ y$, $ z$ -- proekcii vektora $ {\bf r}$ (2.3) na vektory $ {\bf i}$, $ {\bf j}$, $ {\bf k}$, sootvetstvenno. Ispol'zuya matrichnye oboznacheniya, eto vyrazhenie mozhno zapisat' v vide:

$\displaystyle {\bf r} = \begin{pmatrix}{\bf i} & {\bf j} & {\bf k} \end{pmatrix} \begin{pmatrix}x \\ y \\ z \end{pmatrix},$ (3.7)

gde zapis' ( $ {\bf i}\ {\bf j}\ {\bf k}$) oboznachaet vektor-stroku. Ostavim oboznachenie ( $ {\bf i}\ {\bf j}\ {\bf k}$) dlya bazisnoi troiki vektorov ekvatorial'noi sistemy. Bazisnye troiki vektorov eklipticheskoi i galakticheskoi sistemy koordinat oboznacheny v § 3.3 i 3.4 kak ( $ {\bf i}_e\ {\bf j}_e\ {\bf k}_e$) i ( $ {\bf i}_g\ {\bf j}_g\ {\bf k}_g$), sootvetstvenno.

Razlozhim radius-vektor odnogo i togo zhe nebesnogo ob'ekta po bazisnym troikam ekvatorial'noi, eklipticheskoi i galakticheskoi sistem. Dlya etogo ispol'zuem formulu (2.20), v kotoroi koordinaty $ \theta, \lambda$ zamenyayutsya na $ \alpha,\delta$, ili $ \beta,\lambda$, ili $ b,l$, i zapishem matrichnoe ravenstvo (3.5) v vide:

$\displaystyle {\bf r} = \begin{pmatrix}{\bf i}&{\bf j}&{\bf k} \end{pmatrix} \begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin\delta \end{pmatrix} = \begin{pmatrix}{\bf i}_e&{\bf j}_e&{\bf k}_e \end{pmatrix} \begin{pmatrix}\cos\beta \cos\lambda \\ \cos\beta \sin\lambda \\ \sin\beta \end{pmatrix} = \begin{pmatrix}{\bf i}_g&{\bf j}_g&{\bf k}_g \end{pmatrix} \begin{pmatrix}\cos b\cos l \\ \cos b\sin l \\ \sin l \end{pmatrix}.$ (3.8)

Chtoby naiti preobrazovanie ot odnoi sistemy koordinat k drugoi, nado naiti matricu povorota ot odnoi bazisnoi troiki k drugoi. Naprimer, naidem preobrazovanie ot ekvatorial'noi k eklipticheskoi sisteme. Togda

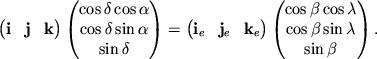
$\displaystyle \begin{pmatrix}{\bf i} & {\bf j} & {\bf k} \end{pmatrix}\begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin \delta \end{pmatrix} = \begin{pmatrix}{\bf i}_e & {\bf j}_e & {\bf k}_e \end{pmatrix}\begin{pmatrix}\cos\beta \cos\lambda \\ \cos\beta \sin\lambda \\ \sin \beta \end{pmatrix}. $

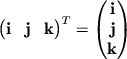Umnozhim obe chasti uravneniya na vektor-stolbec $ \begin{pmatrix}{\bf i} & {\bf j} & {\bf k} \end{pmatrix} ^{T}$ sleva, gde indeks "T" oboznachaet transponirovanie, t.e. $ \begin{pmatrix}{\bf i} & {\bf j} & {\bf k} \end{pmatrix}^{T} = \begin{pmatrix}{\bf i} \\ {\bf j} \\ {\bf k} \end{pmatrix}$. V rezul'tate poluchim

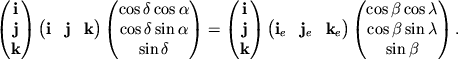
$\displaystyle \begin{pmatrix}{\bf i} \\ {\bf j} \\ {\bf k} \end{pmatrix}\begin{pmatrix}{\bf i} & {\bf j} & {\bf k} \end{pmatrix}\begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin \delta \end{pmatrix} = \begin{pmatrix}{\bf i} \\ {\bf j} \\ {\bf k} \end{pmatrix}\begin{pmatrix}{\bf i}_e & {\bf j}_e & {\bf k}_e \end{pmatrix}\begin{pmatrix}\cos\beta \cos\lambda \\ \cos\beta \sin\lambda \\ \sin \beta \end{pmatrix}. $

Po opredeleniyu skalyarnogo proizvedeniya i pravilu umnozheniya matric imeem:

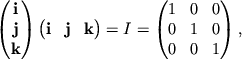
$\displaystyle \begin{pmatrix}{\bf i} \\ {\bf j} \\ {\bf k} \end{pmatrix}\begin{pmatrix}{\bf i} & {\bf j} & {\bf k} \end{pmatrix} = I = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, $

gde $ I$ -- edinichnaya matrica.

Takim obrazom preobrazovanie ot eklipticheskoi k ekvatorial'noi sisteme mozhno zapisat' sleduyushim obrazom:

$\displaystyle \begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin \delta \end{pmatrix} = A_e \begin{pmatrix}\cos\beta \cos\lambda \\ \cos\beta \sin\lambda \\ \sin \beta \end{pmatrix},$ (3.9)

gde

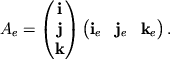
$\displaystyle A_e = \begin{pmatrix}{\bf i} \\ {\bf j} \\ {\bf k} \end{pmatrix}\begin{pmatrix}{\bf i}_e & {\bf j}_e & {\bf k}_e \end{pmatrix}. $

Vychislim matricu $ A_e$ v yavnom vide, ispol'zuya ris. 3.7.

Ris. 3.7. Raspolozhenie osei ekvatorial'noi i eklipticheskoi sistem koordinat

V obeih sistemah os' $ Ox$ napravlena v tochku vesennego ravnodenstviya $ \aries$. Poetomu napravlenie vektorov $ {\bf i}$ i $ {\bf i}_e$ sovpadaet. Osi $ Oz$ i $ Oz'$ napravleny sootvetstvenno v polyus mira $ P_N$ i polyus ekliptiki $ \Pi_N$. Sledovatel'no ugol mezhdu vektorami $ {\bf k}$ i $ {\bf k}_e$ raven $ \varepsilon$. Ugol mezhdu vektorami $ {\bf j}$ i $ {\bf j}_e$ takzhe raven $ \varepsilon$. Ispol'zuya opredelenie skalyarnogo proizvedeniya, poluchim:

$\displaystyle A_e = \begin{pmatrix}{\bf i}\cdot{\bf i}_e & {\bf i}\cdot{\bf j}_e & {\bf i}\cdot{\bf k}_e \\ {\bf j}\cdot{\bf i}_e & {\bf j}\cdot{\bf j}_e & {\bf j}\cdot{\bf k}_e \\ {\bf k}\cdot{\bf i}_e & {\bf k}\cdot{\bf j}_e & {\bf k}\cdot{\bf k}_e \end{pmatrix} = \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos\varepsilon & \cos (90^\circ+\varepsilon) \\ 0 & \cos(90^\circ-\epsilon) & \cos\epsilon \end{pmatrix} = \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos\varepsilon & -\sin\varepsilon \\ 0 & \sin\varepsilon & \cos\varepsilon \end{pmatrix}.$ (3.10)

Uravneniya (3.7) i (3.8) odnoznachno opredelyayut svyaz' mezhdu dvumya sistemami koordinat, i udobny pri vychislenii na komp'yutere. Tem ne menee privedem preobrazovanie (3.7) v yavnom vide:

$\displaystyle \cos\delta \cos\alpha$ $\displaystyle = \cos\beta \cos\lambda,$ (11)
$\displaystyle \cos\delta \sin\alpha$ $\displaystyle = \cos\beta \sin\lambda \cos\varepsilon - \sin\beta \sin\varepsilon,$ (12)
$\displaystyle \sin \delta$ $\displaystyle = \cos\beta \sin\lambda \sin\varepsilon + \sin \beta \cos \varepsilon.$ (13)

Ispol'zuya matrichnuyu zapis' (3.7) legko naiti obratnoe preobrazovanie ot ekvatorial'noi k eklipticheskoi sisteme koordinat. Dlya etogo umnozhim uravnenie (3.7) sleva na matricu, obratnuyu $ A_e$, t.e. na $ A_e^{-1}$:

$\displaystyle A^{-1}_e \begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin \delta \end{pmatrix} = \begin{pmatrix}\cos\beta \cos\lambda \\ \cos \beta \sin \lambda \\ \sin \beta \end{pmatrix}.$ (3.14)

Matrica $ A_e$ obladaet special'nymi svoistvami. Netrudno proverit', chto $ A^T_e A_e = A_e A^T_e = I$, t.e. $ A_e^T = A_e^{-1}$. Podobnye matricy nazyvayutsya ortogonal'nymi. Preobrazovanie (3.12) imeet, takim obrazom, vid:

$\displaystyle \begin{pmatrix}\cos\beta \cos\lambda \\ \cos\beta \sin\lambda \\ \sin \beta \end{pmatrix} = A^T_e \begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin \delta \end{pmatrix} = \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos\varepsilon & \sin\varepsilon \\ 0 & -\sin\varepsilon & \cos\varepsilon \end{pmatrix} \begin{pmatrix}\cos\delta \cos\alpha \\ \cos\delta \sin\alpha \\ \sin \delta \end{pmatrix}.$ (3.15)

Matrica $ A^T_e$ opisyvaet preobrazovanie ot ekvatorial'noi sistemy k eklipticheskoi. Vrashenie na ugol $ \varepsilon$ dlya sovmesheniya osei $ Oy$ i $ Oz$ s osyami $ Oy'$ i $ Oz'$, sootvetstvenno, nazyvaetsya pravym, tak kak pri etom dvizhenie voobrazhaemogo pravogo vinta sovpadaet s napravleniem osi $ Ox$. Matrica $ A^T_e$, poetomu, opisyvaet pravoe vrashenie otnositel'no osi $ Ox$.

V yavnom vide iz (3.13) poluchim:

$\displaystyle \cos \beta \cos \lambda =$ $\displaystyle \cos\delta \cos\alpha$    
$\displaystyle \cos \beta \sin \lambda =$ $\displaystyle \cos \delta \sin \alpha \cos \varepsilon +\sin \delta \sin \varepsilon$ (16)
$\displaystyle \sin \beta = -$ $\displaystyle \cos \delta \sin \alpha \sin \varepsilon + \sin \delta \cos \varepsilon .$    

Analogichno mogut byt' polucheny matricy vrashenii otnositel'no osei $ Oy$ i $ Oz$. Dlya sohraneniya obshnosti izlozheniya oboznachim matricy povorotov otnositel'no osei $ Ox$, $ Oy$, $ Oz$ na ugol $ \phi$ kak $ R_1(\phi)$, $ R_2(\phi)$, $ R_3(\phi)$ sootvetstvenno, prichem

$\displaystyle R_1 (\phi) = \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos \phi & \sin \phi \\ 0 & -\sin \phi & \cos \phi \end{pmatrix}; R_2 (\phi) = \begin{pmatrix}\cos \phi & 0 & -\sin \phi \\ 0 & 1 & 0 \\ \sin \phi & 0 & \cos \phi \end{pmatrix}; R_3 (\phi) = \begin{pmatrix}\cos\phi & \sin\phi & 0 \\ -\sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix}.$ (3.17)

Matrica $ A_e$ (3.8) ravna, sledovatel'no, $ R_1(-\varepsilon)$, t.e. dlya perehoda ot eklipticheskoi k ekvatorial'noi sisteme neobhodimo povernut' osi eklipticheskoi sistemy otnositel'no osi $ Ox$ ($ Ox'$) na ugol $ -\varepsilon$.

S pomosh'yu matric (3.15) mozhno vychislit' lyubuyu matricu, opisyvayushuyu vrashenie v trehmernom prostranstve.

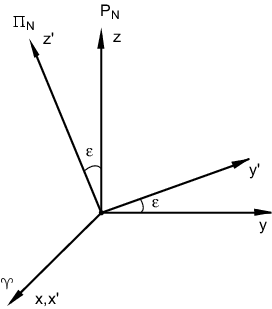
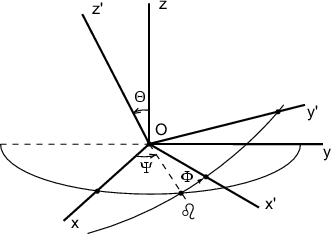
Rassmotrim dve dekartovy sistemy koordinat: $ Oxyz$ i $ Ox'y'z'$ (ris. 3.8).

Ris. 3.8. Opredelenie uglov Eilera

Naidem matricu preobrazovaniya $ R$ koordinat vektora iz sistemy $ Oxyz$ k sisteme $ Ox'y'z'$. Dlya etogo snachala povernem sistemu $ Oxyz$ otnositel'no osi $ Oz$ na ugol $ \Psi$ (do sovmesheniya osi $ Ox$ s liniei uzlov $ O\ascnode$). Vrashenie otnositel'no linii uzlov (kotoraya teper' sovpadaet s os'yu $ Ox$) na ugol $ \Theta$ privedet k sovmesheniyu osi $ Oz$ s os'yu $ Oz'$. I, nakonec, povorot otnositel'no osi $ Oz'$ na ugol $ \Phi$ perevodit os' $ Ox$ v polozhenie $ Ox'$ ($ Oy$ v $ Oy'$ sootvetstvenno). Vse povoroty -- polozhitel'ny.

Ugly $ \Psi$, $ \Theta$, $ \Phi$ nazyvayutsya uglami Eilera. Tri ugla Eilera odnoznachno opredelyayut povorot odnoi sistemy koordinat otnositel'no drugoi. V teoreticheskoi mehanike i astronomii eti ugly imeyut sobstvennye nazvaniya. Esli osi $ Ox$, $ Oy$ lezhat v ploskosti ekliptiki, to ugol $ \Psi$ nazyvaetsya uglom precessii. Ugol $ \Theta$ est' ugol nutacii, a ugol $ \Phi$ nazyvaetsya uglom sobstvennogo vrasheniya.

Matrica vrasheniya $ R$ ravna proizvedeniyu treh matric (obratite vnimanie na poryadok peremnozheniya matric i posledovatel'nost' vrashenii):

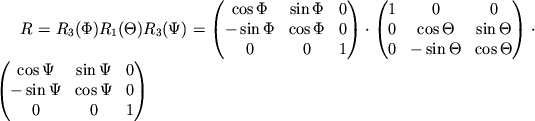
$\displaystyle R=R_3 (\Phi) R_1 (\Theta) R_3 (\Psi) = \begin{pmatrix}\cos\Phi & \sin\Phi & 0 \\ -\sin\Phi & \cos\Phi & 0 \\ 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos\Theta & \sin\Theta \\ 0 & -\sin\Theta & \cos\Theta \end{pmatrix}\cdot \begin{pmatrix}\cos\Psi & \sin\Psi & 0 \\ -\sin\Psi & \cos\Psi & 0 \\ 0 & 0 & 1 \end{pmatrix}$

ili

$\displaystyle R=\begin{pmatrix}\cos\Phi\cos\Psi - \sin\Phi\cos\Theta\sin\Psi & \cos\Phi\sin\Psi + \sin\Phi\cos\Theta\cos\Psi & \sin\Phi\sin\Theta \\ -\sin\Phi\cos\Psi - \cos\Phi\cos\Theta\sin\Psi & -\sin\Phi\sin\Psi + \cos\Phi\cos\Theta\cos\Psi & \cos\Phi\sin\Theta \\ \sin\Theta\sin\Psi & -\sin\Theta\cos\Psi & \cos\Theta \end{pmatrix}.$ (3.18)

S pomosh'yu matrichnogo metoda legko naiti matricu preobrazovaniya ekvatorial'nyh koordinat ($ \alpha$, $ \delta$) v galakticheskie koordinaty ($ l$,$ b$) (ris. 3.5).

Iz uravneniya (3.6) imeem:

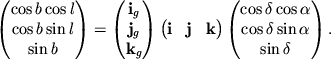
$\displaystyle \begin{pmatrix}\cos b\cos l \\ \cos b\sin l \\ \sin b \end{pmatrix} = \begin{pmatrix}{\bf i}_g \\ {\bf j}_g \\ {\bf k}_g \end{pmatrix}\begin{pmatrix}{\bf i}& {\bf j}& {\bf k} \end{pmatrix}\begin{pmatrix}\cos\delta\cos\alpha \\ \cos\delta\sin\alpha \\ \sin\delta \end{pmatrix}. $

Napomnim, chto ort $ {\bf i}$ napravlen v tochku vesennego ravnodenstviya $ \aries$, $ {\bf j}$ -- v tochku s pryamym voshozhdeniem, ravnym $ 90^\circ$, i $ {\bf k}$ -- v severnyi polyus mira. Soglasno opredeleniyu vektor $ {\bf i}_g$ napravlen v centr Galaktiki, $ {\bf k}_g$ -- v severnyi polyus $ G_N$ (§ 3.4).

Matrica

$\displaystyle A_G=\begin{pmatrix}{\bf i}_g \\ {\bf j}_g \\ {\bf k}_g \end{pmatrix} \begin{pmatrix}{\bf i}& {\bf j}& {\bf k} \end{pmatrix}$ (3.19)

yavlyaetsya iskomoi matricei preobrazovaniya.

Dovol'no trudno vychislit' skalyarnye proizvedeniya $ {\bf i}_g\cdot{\bf i}$, $ {\bf i}_g\cdot{\bf j}$ i t.d. neposredstvenno. Poetomu vychislim matricu (3.17), sootvetstvuyushuyu perehodu ot ekvatorial'noi sistemy k galakticheskoi sleduyushim obrazom (sm. ris. 3.5): vypolnim pervoe vrashenie otnositel'no osi mira na ugol $ \alpha_{\ascnode}$ (pryamoe voshozhdenie tochki $ \ascnode$), t. e. vychislyaem matricu $ R_3(\alpha_{\ascnode})$, zatem vypolnyaem vrashenie otnositel'no linii uzlov na ugol $ 90^\circ-\delta_{G_N}$ i vychislyaem matricu $ R_1(90^\circ-\delta_{G_N})$, gde $ \delta_{G_N}$ -- sklonenie severnogo galakticheskogo polyusa. Tretii povorot -- eto povorot otnositel'no osi, soedinyayushei severnyi i yuzhnyi polyusa Galaktiki, na ugol $ -l_{\ascnode}$. V rezul'tate matrica $ A_G$ zapisyvaetsya v vide:

$\displaystyle A_G=R_3 (-l_{\ascnode})\cdot R_1(90^\circ-\delta_{G_N})\cdot R_3 (\alpha_{\ascnode}). $

Zametim, chto $ \alpha_{\ascnode} = \alpha_{G_N} + 90^\circ$, $ \alpha_{G_N}$ -- pryamoe voshozhdenie severnogo galakticheskogo polyusa. Eto sleduet iz togo, chto dvugrannyi ugol $ G_N P_N \ascnode$ raven $ 90^\circ$. Zamenyaya simvol $ \phi$ v (3.15) na sootvetstvuyushie ugly, poluchim:

$\displaystyle A_G =\begin{pmatrix}\cos l_{\ascnode} & -\sin l_{\ascnode} & 0 \\ \sin l_{\ascnode} & \cos l_{\ascnode} & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix}1 & 0 & 0 \\ 0 & \sin\delta_G & \cos\delta_G \\ 0 & -\cos\delta_G & \sin\delta_G \end{pmatrix} \begin{pmatrix}\cos\alpha_{\ascnode} & \sin\alpha_{\ascnode} & 0 \\ -\sin\alpha_{\ascnode} & \cos\alpha_{\ascnode} & 0 \\ 0 & 0 & 1 \end{pmatrix}$ (3.20)

Podstaviv znacheniya uglov i vychisliv proizvedenie matric, poluchim:

$\displaystyle A_G =\begin{pmatrix}-0.0548755601367195 & -0.8734370902532698 & -0.4838350155472244 \\ +0.4941094280132430 & -0.4448296298016944 & +0.7469822445004389 \\ -0.8676661489582886 & -0.1980763737056720 & +0.4559837761713720 \end{pmatrix}.$ (3.21)

Obratnoe preobrazovanie (ot galakticheskoi k ekvatorial'noi sisteme koordinat) vyrazhaetsya matrichnym uravneniem:

$\displaystyle \begin{pmatrix}\cos\delta\cos\alpha \\ \cos\delta\sin\alpha \\ \sin\delta \end{pmatrix} = A^{-1}_G \begin{pmatrix}\cos b\cos l \\ \cos b\sin l \\ \sin b \end{pmatrix}$ (3.22)

Tak kak matrica $ A_G$ -- ortogonal'naya, to $ A^{-1}_G = A^T_G$.

V zaklyuchenie ispol'zuem matrichnyi metod dlya vychisleniya matricy preobrazovaniya ot gorizontal'noi ($ z,A$) k ekvatorial'noi sisteme koordinat ($ t,\delta$) (ris. 3.3 i 3.6). Dlya etogo dostatochno vypolnit' odin povorot: otnositel'no osi $ -Oy$ (obe sistemy koordinat -- levye) na ugol $ -(90^\circ-\varphi)$, gde $ \varphi$ -- astronomicheskaya shirota. Sledovatel'no matrichnoe uravnenie preobrazovaniya koordinat mozhno zapisat' kak

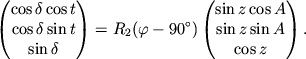$\displaystyle \begin{pmatrix}\cos\delta \cos t \\ \cos\delta \sin t \\ \sin \delta\end{pmatrix} =R_2(\varphi-90^\circ) \begin{pmatrix}\sin z \cos A \\ \sin z \sin A \\ \cos z \end{pmatrix}.$ (3.23)

Legko proverit', chto eta sistema sovpadaet s uravneniyami (3.4).



Ispol'zuem poluchennye formuly preobrazovaniya koordinat dlya resheniya sleduyushih zadach.

Zadacha 1. Naiti geometricheskoe mesto tochek na nebesnoi sfere, u kotoryh sklonenie $ \delta$ ravno eklipticheskoi shirote $ \beta$.

Reshenie. Preobrazovanie koordinat tochki iz ekvatorial'noi v eklipticheskuyu sistemu zadaetsya uravneniyami (3.14):

$\displaystyle \cos \beta \cos \lambda =$ $\displaystyle \cos \delta \cos \alpha,$    
$\displaystyle \cos \beta \sin \lambda =$ $\displaystyle \cos \delta \sin \alpha \cos \varepsilon +\sin \delta \sin \varepsilon,$    
$\displaystyle \sin \beta = -$ $\displaystyle \cos \delta \sin \alpha \sin \varepsilon + \sin \delta \cos \varepsilon .$    

Iz pervogo uravneniya poluchim: $ \cos \lambda = \cos \alpha$. Esli iz vtorogo uravneniya vyrazit' $ \sin\alpha$ i podstavit' v tret'e, to naidem, chto $ \sin\lambda=-\sin\alpha$. Resheniem etoi sistemy budet $ \alpha=-\lambda$.

Ochevidno, chto v tochke vesennego ravnodenstviya $ \delta=\beta = 0$, takzhe $ \alpha=\lambda = 0$; v tochke osennego ravnodenstviya $ \delta=\beta = 0$, $ \alpha=\lambda = 180^\circ$. Geometricheskim mestom na sfere, udovletvoryayushim usloviyu $ \delta=\beta=\kappa$ ($ \kappa$ -- nekotoroe chislo), yavlyaetsya tochka sfericheskogo treugol'nika, odnoi iz storon kotorogo yavlyaetsya duga mezhdu polyusom mira i polyusom ekliptiki i ravnaya $ \varepsilon$, dvumya drugimi -- dugi s dlinoi $ 90^\circ-\kappa$. Pri uvelichenii $ \kappa$ do $ 90^\circ$ treugol'nik vyrozhdaetsya v dugu, a tochka podnimaetsya po duge okruzhnosti, prohodyashei poseredine mezhdu polyusom mira i polyusom ekliptiki.

Takim obrazom, geometricheskim mestom tochek na nebesnoi sfere budet okruzhnost' -- peresechenie bol'shogo kruga, naklonennogo k ekvatoru pod uglom $ 90^\circ+\varepsilon/2$ i prohodyashego cherez tochki ravnodenstviya, s nebesnoi sferoi.



Zadacha 2. Naiti geometricheskoe mesto tochek na nebesnoi sfere, u kotoryh pryamoe voshozhdenie $ \alpha$ ravno eklipticheskoi dolgote $ \lambda$.

Reshenie. Po analogii s predydushei zadachei poluchim dva uravneniya:

$\displaystyle \cos \beta$ $\displaystyle =\cos \delta ,$    
$\displaystyle \sin\beta$ $\displaystyle =-\sin\delta,$    

kotorye udovletvoryayutsya pri $ \beta=-\delta$. Legko dokazat', chto geometricheskim mestom na nebesnoi sfere, sootvetstvuyushim usloviyu $ \beta=-\delta$, budet okruzhnost' -- peresechenie sfery s bol'shim krugom, naklonennym k ekvatoru pod uglom $ \varepsilon/2$.



Zadacha 3. Kakovo pryamoe voshozhdenie i sklonenie severnogo i yuzhnogo polyusa ekliptiki?

Reshenie. Koordinaty polyusov ekliptiki mozhno naiti, reshaya uravneniya (3.14). Odnako proshe naiti reshenie, vospol'zovavshis' ris. 3.7. Dlya sovmesheniya osei dvuh sistem dostatochno povernut' ekvatorial'nuyu sistemu otnositel'no osi $ Ox$ na ugol $ \varepsilon$, t.e. polyusy ekliptiki lezhat v ploskosti $ Oyz$. Znachit, koordinaty severnogo polyusa ekliptiki ravny $ \alpha =270^\circ, \delta=90^\circ-\varepsilon$, a yuzhnogo -- $ \alpha =90^\circ, \delta=-90^\circ+\varepsilon$.



Zadacha 4. V kakih tochkah Zemli ekliptika mozhet sovpadat' s pervym vertikalom?

Reshenie. Napomnim, chto pervym vertikalom nazyvaetsya vertikal'nyi krug, prohodyashii cherez tochki vostoka i zapada, t.e. ekliptika dolzhna prohodit' cherez zenit nablyudatelya i tochki vostoka i zapada. Znachit severnyi polyus ekliptiki dolzhen nahodit'sya v ploskosti gorizonta nablyudatelya i sovpadat' s tochkoi severa. Eto vozmozhno, esli shirota nablyudatelya ravna $ \varepsilon$, t.e. nablyudatel' nahoditsya severnom tropike. Solnce voshodit v tochke vostoka, dvizhetsya cherez zenit nablyudatelya i zahodit v tochke zapada. Esli vstat' licom k severu, to Solnce vstaet sprava, zahodit sleva.

V yuzhnom polusharii analogichnaya kartina nablyudaetsya, esli nablyudatel' nahoditsya na yuzhnom tropike (shirota ravna $ -\varepsilon$). Odnako kazhetsya, chto nebesnaya sfera vrashaetsya v protivopolozhnuyu storonu; Solnce vstaet sleva, zahodit sprava, esli vstat' licom k yugu.


<< 3.4. Galakticheskaya sistema koordinat | Oglavlenie | 3.6. Sutochnoe vrashenie nebesnoi >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]
Ocenka: 3.5 [golosov: 304]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya