Astronet > Sfericheskaya astronomiya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 3.5. Preobrazovanie koordinat iz | Oglavlenie | 3.7. Voshod i zahod >>

3.6. Sutochnoe vrashenie nebesnoi sfery

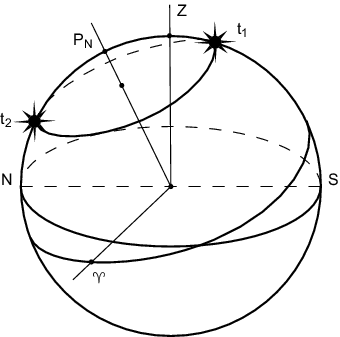
Iz-za vrasheniya Zemli vokrug svoei osi kazhetsya, chto nebesnaya sfera vrashaetsya vokrug osi mira, kotoraya parallel'na osi vrasheniya Zemli. V rezul'tate etogo cherez nebesnyi meridian periodicheski prohodyat zvezdy, Solnce i drugie svetila.

Opredelenie 3.6.1 Moment prohozhdeniya zvezdy cherez meridian nazyvaetsya kul'minaciei zvezdy.

Ta iz dvuh kul'minacii, kotoraya proishodit blizhe k zenitu, nazyvaetsya verhnei, vtoraya -- nizhnei. Dlya nablyudatelya v severnom polusharii verhnyaya kul'minaciya proishodit k yugu ot severnogo polyusa mira (moment $t_{1}$ ), a nizhnyaya -- k severu ot tochki $P_{N}$ (moment $t_{2}$ ) (ris. 3.9).

Ris. 3.9. Verhnyaya i nizhnyaya kul'minacii zvezdy dlya nablyudatelya v severnom polusharii

Ochevidno, chto promezhutok vremeni mezhdu $t_{1}$ i $t_{2}$ raven $12^h$ (ili $180^\circ$ v uglovoi mere).

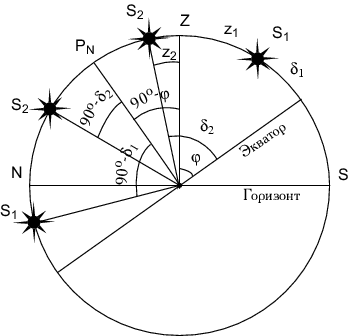
Iz ris. 3.10 yasno, chto dlya zvezdy $S_1$ , kul'miniruyushei k yugu ot zenita, $\varphi =z_1+\delta_1$ , togda kak dlya zvezdy $S_2$ , kul'miniruyushei k severu ot zenita, spravedlivo ravenstvo $\varphi =\delta_2 -z_2$ .

Ris. 3.10. Zahodyashie i nezahodyashie zvezdy

Takim obrazom v verhnei kul'minacii imeem:

$\displaystyle \textrm{dlya}\ S_1:\qquad z_u=\varphi -\delta,\ \textrm{ esli}\ \varphi\gt \delta;$

(3.24)

$\displaystyle \textrm{dlya}\ S_2:\qquad z_u=\delta -\varphi,\ \textrm{esli}\ \varphi \lt \delta.$

(3.25)

Dlya nizhnei kul'minacii poluchim:

$\displaystyle z_l=(90^\circ-\varphi)+(90^\circ-\delta)=180^\circ-(\varphi+\delta).$

(3.26)

Zenitnoe rasstoyanie zvezdy v verhnei (nizhnei) kul'minacii yavlyaetsya minimal'nym (maksimal'nym) zenitnym rasstoyaniem. V zavisimosti ot velichin $z_u$ i $z_l$ zvezdy mozhno razdelit' na nezahodyashie, nevoshodyashie, voshodyashie i zahodyashie. Esli v nizhnei kul'minacii $z_l\lt 90^\circ$ , to zvezda vsegda nahoditsya nad gorizontom. Iz (3.24) sleduet: chto

$\displaystyle z_l=180^\circ-(\varphi +\delta )\lt 90^\circ .$

Dlya nezahodyashih zvezd v severnom polusharii vypolnyaetsya sootnoshenie:

$\displaystyle \delta \gt 90^\circ-\varphi.$

Dlya nevoshodyashih zvezd zenitnoe rasstoyanie v verhnei kul'minacii $z_u\gt 90^\circ$ ,t.e. $\varphi -\delta \gt 90^\circ$ ili $\delta \lt -(90^\circ-\varphi)$ . Takim obrazom, esli sklonenie zvezdy $\delta$ udovletvoryaet usloviyu

$\displaystyle -(90^\circ-\varphi)\lt \delta \lt 90^\circ-\varphi,$

to zvezda periodicheski voshodit i zahodit.

Chasto nablyudeniya zvezdy v verhnei i nizhnei kul'minaciyah ispol'zuetsya dlya opredeleniya shiroty mesta ili skloneniya zvezdy. Esli pri pomoshi nablyudenii polucheny $z_u$ i $z_l$ , to, skladyvaya (3.23) i (3.24), poluchim:

$\displaystyle \varphi =90^\circ-\frac{z_u+z_l}{2}.$

V etom sluchae ne trebuetsya znat' sklonenie zvezdy. Obratno, sklonenie zvezdy mozhet byt' naideno, esli neizvestna shirota mesta iz uravneniya:

$\displaystyle \delta =90^\circ+\frac{z_u-z_l}{2}.$

<< 3.5. Preobrazovanie koordinat iz | Oglavlenie | 3.7. Voshod i zahod >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni

Sm. takzhe:

Dostizheniya kosmicheskoi astrometrii

Skonchalsya Konstantin Vladislavovich Kuimov

Konstantinu Vladislavovichu Kuimovu – 75 let

Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya.

Vrashenie Zemli i prodolzhitel'nost' sutok

80 let so dnya rozhdeniya Al'berta Petrovicha Gulyaeva

Rukovodstvo po prakticheskoi rabote s katalogom Hipparcos

Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce