3.7. Voshod i zahod nebesnyh tel
V moment voshoda i zahoda nebesnogo tela ego zenitnoe rasstoyanie
![]() . Togda formulu (3.1) mozhno preobrazovat' k vidu:
. Togda formulu (3.1) mozhno preobrazovat' k vidu:
Znaya sklonenie
Vozmozhny tri sluchaya.
- Kazhdoe iz uravnenii (3.25), (3.26) imeet dva resheniya
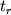 ,
,
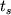 : znachenie
: znachenie 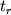 lezhit mezhdu
lezhit mezhdu 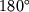 i
i 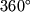 -- v
etot moment nebesnoe telo voshodit; znachenie
-- v
etot moment nebesnoe telo voshodit; znachenie 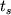 lezhit mezhdu
lezhit mezhdu
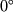 i
i 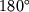 i yavlyaetsya momentom zahoda. Eto oznachaet,
chto nebesnoe telo periodicheski voshodit i zahodit.
i yavlyaetsya momentom zahoda. Eto oznachaet,
chto nebesnoe telo periodicheski voshodit i zahodit.
Azimut v tochkah voshoda i zahoda opredelyaetsya iz sistemy uravnenii:
gde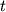 ravnyaetsya
ravnyaetsya 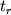 ili
ili 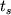 . Azimut v tochke voshoda mozhet
prinimat' znacheniya
. Azimut v tochke voshoda mozhet
prinimat' znacheniya
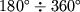 , v tochke zahoda --
, v tochke zahoda --
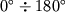 .
.
Chtoby naiti vremya voshoda (zahoda), neobhodimo k chasovomu uglu
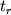 (ili
(ili 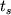 ) pribavit' pryamoe voshozhdenie
) pribavit' pryamoe voshozhdenie 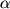 nebesnogo
tela:
gde
nebesnogo
tela:
gde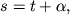
 -- mestnoe zvezdnoe vremya. Opredelenie zvezdnogo vremeni
budet dano nizhe (sm. §
5.2).
-- mestnoe zvezdnoe vremya. Opredelenie zvezdnogo vremeni
budet dano nizhe (sm. §
5.2).
- Esli uravneniya (3.25), (3.26) imeyut odno reshenie, to eto
oznachaet, chto nebesnoe telo kasaetsya gorizonta. Esli eto sobytie
proishodit vo vremya nizhnei kul'minacii, to
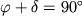 . Pri etom iz (3.26) poluchim:
. Pri etom iz (3.26) poluchim:
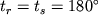 , a iz (3.27)
, a iz (3.27)
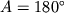 . Esli nebesnoe
telo dostigaet ploskosti gorizonta vo vremya verhnei kul'minacii,
to
. Esli nebesnoe
telo dostigaet ploskosti gorizonta vo vremya verhnei kul'minacii,
to
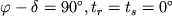 ,
, 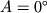 .
.
- Esli pravaya chast' uravneniya (3.25) bol'she 1 ili men'she -1, to
uravnenie ne imeet reshenii, t.e. voshod i zahod nevozmozhny. Chtoby
reshit' vopros, yavlyaetsya li nebesnoe telo nezahodyashim ili
nevoshodyashim v severnom polusharii, nado proverit' neravenstva:
V pervom sluchae telo yavlyaetsya nezahodyashim, vo vtorom -- nevoshodyashim.
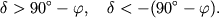
Zametim v konce paragrafa, chto pri vyvode formuly (3.25) ne uchityvalos' yavlenie refrakcii (§6.1), kotoroe privodit k pod'emu svetila nad gorizontom otnositel'no ego istinnogo polozheniya. V rezul'tate refrakcii vremya voshoda nastupaet na neskol'ko minut ran'she, a vremya zahoda -- na neskol'ko minut pozzhe vychislennogo po formulam (3.25), (3.26).
<< 3.6. Sutochnoe vrashenie nebesnoi | Oglavlenie | 3.8. Opredelenie sistem koordinat >>
|
Publikacii s klyuchevymi slovami:
astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
Mneniya chitatelei [13]
Astrometriya
-
Astronomicheskie instrumenty
-
Astronomicheskoe obrazovanie
-
Astrofizika
-
Istoriya astronomii
-
Kosmonavtika, issledovanie kosmosa
-
Lyubitel'skaya astronomiya
-
Planety i Solnechnaya sistema
-
Solnce