3.10.1. Zakony Keplera
Dlya opredeleniya sistemy koordinat neobhodimo snachala opredelit'
ploskost', zatem v ploskosti opredelit' napravlenie na
vydelennuyu tochku. Togda s edinichnym vektorom
![]() ,
napravlennym v etu tochku, mozhno svyazat' os'
,
napravlennym v etu tochku, mozhno svyazat' os' ![]() , s
perpendikulyarom k ploskosti -- edinichnyi vektor
, s
perpendikulyarom k ploskosti -- edinichnyi vektor
![]() i
os'
i
os' ![]() ; edinichnyi vektor
; edinichnyi vektor
![]() (os'
(os' ![]() sistemy koordinat)
opredelyaetsya na osnove vektornogo proizvedeniya tak, chtoby
sistema osei byla pravoi (
sistemy koordinat)
opredelyaetsya na osnove vektornogo proizvedeniya tak, chtoby
sistema osei byla pravoi (
![]() ).
).
Rassmotrim vopros, kak v prostranstve opredelit' etu ploskost' i osi, lezhashie v ploskosti.
V osnove dinamicheskogo metoda opredeleniya sistemy koordinat lezhat
uravneniya dinamiki -- i v pervuyu ochered' zakon prityazheniya
N'yutona. Soglasno etomu zakonu dva tela s massami ![]() i
i ![]() prityagivayutsya s siloi
prityagivayutsya s siloi
![]() , gde
, gde ![]() -- rasstoyanie mezhdu
telami. Koefficient
-- rasstoyanie mezhdu
telami. Koefficient
![]() nazyvaetsya postoyannoi
tyagoteniya. Esli tela raspolozheny v tochkah
nazyvaetsya postoyannoi
tyagoteniya. Esli tela raspolozheny v tochkah ![]() i
i ![]() s
dekartovymi koordinatami
s
dekartovymi koordinatami
![]() i
i
![]() ,
sootvetstvenno, to dvizhenie tela s massoi
,
sootvetstvenno, to dvizhenie tela s massoi ![]() opisyvaetsya
uravneniyami:
opisyvaetsya
uravneniyami:
tochkami oboznacheno differencirovanie po vremeni:
Vvedem oboznacheniya:
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Vychitaya iz uravnenii (3.28)
uravneniya (3.29), poluchim
. Vychitaya iz uravnenii (3.28)
uravneniya (3.29), poluchim
V uravneniya (3.30-3.32) vhodyat lish' otnositel'nye koordinaty dvuh tochek, t.e. uravneniya dvizheniya ne zavisyat ot polozheniya nachala sistemy koordinat. Umnozhaya uravnenie (3.30) na
Iz (3.33) sleduet, chto velichina v skobkah ne zavisit ot vremeni, t.e.
Analogichnym obrazom iz uravnenii (3.31),(3.32) poluchim vyrazhenie:
a iz (3.30) i (3.32):
Uravneniya (3.34-3.36) nazyvayutsya integralami ploshadei, a postoyannye
Umnozhaya uravnenie (3.34) na ![]() , (3.35) -- na
, (3.35) -- na ![]() ,
(3.36) -- na
,
(3.36) -- na ![]() i skladyvaya, nahodim, chto
i skladyvaya, nahodim, chto
Uravnenie (3.37) -- eto uravnenie ploskosti. Znachit, dva tela, dvizhushiesya v prostranstve pod deistviem sily prityazheniya, vsegda nahodyatsya v odnoi i toi zhe ploskosti; traektoriya tela 2 otnositel'no tela 1 yavlyaetsya ploskoi krivoi i nazyvaetsya orbitoi. Drugimi slovami orbita odnogo tela otnositel'no drugogo lezhit v ploskosti.
Raspolozhim osi ![]() sistemy koordinat, kotoruyu my hotim
opredelit' v ploskosti orbity, a os'
sistemy koordinat, kotoruyu my hotim
opredelit' v ploskosti orbity, a os' ![]() budet perpendikulyarna
ei. Tochku
budet perpendikulyarna
ei. Tochku ![]() (nachalo sistemy koordinat) sovmestim s telom s
massoi
(nachalo sistemy koordinat) sovmestim s telom s
massoi ![]() . Togda uravneniya dvizheniya (3.30-3.32) mozhno
zapisat' v vide:
. Togda uravneniya dvizheniya (3.30-3.32) mozhno
zapisat' v vide:
gde
gde
Umnozhim teper' uravneniya (3.30-3.32) sootvetstvenno na
![]() ,
,
![]() ,
,
![]() i slozhim. Koordinaty
i slozhim. Koordinaty
![]() yavlyayutsya koordinatami tela 2 otnositel'no tela 1.
V rezul'tate poluchim sleduyushee uravnenie:
yavlyayutsya koordinatami tela 2 otnositel'no tela 1.
V rezul'tate poluchim sleduyushee uravnenie:
gde
Tak kak orbita lezhit v ploskosti, i polozhenie tela 2 otnositel'no
tela 1 opredelyaetsya lish' koordinatami ![]() , to udobno dlya
dal'neishih vychislenii vvesti polyarnye koordinaty
, to udobno dlya
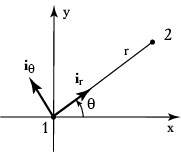
dal'neishih vychislenii vvesti polyarnye koordinaty ![]() (ris. 3.12), tak chto
(ris. 3.12), tak chto
V polyarnoi sisteme koordinat vvedem dva edinichnyh vektora
![]() , prichem pervyi iz nih napravlen
vdol'
, prichem pervyi iz nih napravlen
vdol'
![]() , a vtoroi--perpendikulyaren emu i
napravlen v storonu uvelicheniya ugla
, a vtoroi--perpendikulyaren emu i
napravlen v storonu uvelicheniya ugla ![]() . Togda
. Togda
ili v vektornom vide
Sledovatel'no, v polyarnyh koordinatah uravnenie uglovogo momenta (3.39) imeet vid:
Dopustim, chto v moment ![]() telo 2 nahodilos' na rasstoyanii
telo 2 nahodilos' na rasstoyanii ![]() ot
tela 1, a cherez promezhutok vremeni
ot
tela 1, a cherez promezhutok vremeni ![]() peremestilos' na
ugol
peremestilos' na
ugol
![]() , prichem rasstoyanie stalo ravnyat'sya
, prichem rasstoyanie stalo ravnyat'sya
![]() . Schitaya, chto promezhutok vremeni
. Schitaya, chto promezhutok vremeni ![]() mal, mozhno schitat'
dugu, po kotoroi dvizhetsya telo 2, pryamoi liniei. Togda ploshad'
sektora, kotoryi obrazuyut dva radius-vektora
mal, mozhno schitat'
dugu, po kotoroi dvizhetsya telo 2, pryamoi liniei. Togda ploshad'
sektora, kotoryi obrazuyut dva radius-vektora ![]() i
i
![]() ,
budet blizok k ploshadi treugol'nika, ravnoi
,
budet blizok k ploshadi treugol'nika, ravnoi
![]() . Ustremlyaya
. Ustremlyaya
![]() k nulyu i delya na promezhutok vremeni
k nulyu i delya na promezhutok vremeni
![]() , nahodim, chto ploshad' sektora, opisyvaemaya telom
ravna
, nahodim, chto ploshad' sektora, opisyvaemaya telom
ravna
![]() . Sledovatel'no, na
osnove uravneniya (3.42) mozhno utverzhdat', chto za odinakovye
promezhutki vremeni radius-vektor opisyvaet ravnye ploshadi, prichem
velichina uglovogo momenta ravna udvoennoi ploshadi sektora. Eto
-- vtoroi zakon Keplera.
. Sledovatel'no, na
osnove uravneniya (3.42) mozhno utverzhdat', chto za odinakovye
promezhutki vremeni radius-vektor opisyvaet ravnye ploshadi, prichem
velichina uglovogo momenta ravna udvoennoi ploshadi sektora. Eto
-- vtoroi zakon Keplera.
Zapishem teper' uravnenie (3.38) v polyarnyh koordinatah. Tak kak
proizvodnaya
![]() uzhe naidena (3.41), to
uzhe naidena (3.41), to
Edinichnye vektory
Polagaya, chto
![]() , zapishem uravnenie (3.38)
v polyarnyh koordinatah v sleduyushem vide:
, zapishem uravnenie (3.38)
v polyarnyh koordinatah v sleduyushem vide:
Differencial'nye uravneniya (3.42) i (3.44) opisyvayut
zavisimost' rasstoyaniya ![]() odnogo tela otnositel'no drugogo i ugla
odnogo tela otnositel'no drugogo i ugla
![]() ot vremeni. Dlya resheniya etih uravnenii obychno isklyuchayut
vremya iz (3.44) s pomosh'yu (3.42). Dlya udobstva vvedem
parametr
ot vremeni. Dlya resheniya etih uravnenii obychno isklyuchayut
vremya iz (3.44) s pomosh'yu (3.42). Dlya udobstva vvedem
parametr ![]() , tak chto
, tak chto
Reshenie differencial'nogo uravneniya vtorogo poryadka (3.45) zapisyvaetsya v vide:
Uravnenie (3.46) yavlyaetsya uravneniem konicheskih sechenii. Vid
orbity zavisit ot parametra ![]() -- ekscentrisiteta
orbity. Esli
-- ekscentrisiteta
orbity. Esli
![]() , to traektoriya
yavlyaetsya ellipsom, esli
, to traektoriya
yavlyaetsya ellipsom, esli ![]() , to
-- paraboloi, esli
, to
-- paraboloi, esli ![]() , to -- giperboloi. Vid orbity mozhno
opredelit' takzhe po velichine postoyannoi energii v
uravnenii (3.40), kotoraya zavisit ot skorosti i
radiusa-vektora tela. Poetomu udobno svyazat' vid orbity s
nachal'nymi parametrami
, to -- giperboloi. Vid orbity mozhno
opredelit' takzhe po velichine postoyannoi energii v
uravnenii (3.40), kotoraya zavisit ot skorosti i
radiusa-vektora tela. Poetomu udobno svyazat' vid orbity s
nachal'nymi parametrami ![]() i
i ![]() :
:
Ogranichimsya seichas sluchaem, kogda
![]() . V etom sluchae
uravnenie (3.46) yavlyaetsya matematicheskoi formoi
pervogo zakona Keplera.
. V etom sluchae
uravnenie (3.46) yavlyaetsya matematicheskoi formoi
pervogo zakona Keplera.
Esli telo s massoi ![]() nazvat' Solncem, drugoe telo --
planetoi, to pervyi zakon Keplera formuliruetsya sleduyushim
obrazom: planeta dvizhetsya po ellipsu, v odnom iz fokusov kotorogo
nahoditsya Solnce. Parametr
nazvat' Solncem, drugoe telo --
planetoi, to pervyi zakon Keplera formuliruetsya sleduyushim
obrazom: planeta dvizhetsya po ellipsu, v odnom iz fokusov kotorogo
nahoditsya Solnce. Parametr ![]() nazyvaetsya parametrom ellipsa i
svyazan s bol'shoi poluos'yu
nazyvaetsya parametrom ellipsa i
svyazan s bol'shoi poluos'yu ![]() ellipsa
formuloi:
ellipsa
formuloi:
![]() . Malaya poluos'
. Malaya poluos' ![]() mozhet byt' vyrazhena cherez
mozhet byt' vyrazhena cherez ![]() i
i ![]() :
:
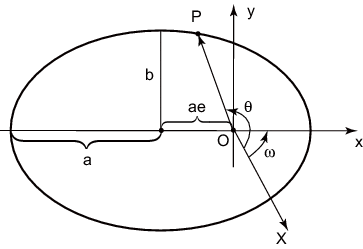
![]() (ris. 3.13). Na ris. 3.13 Solnce nahoditsya v
tochke
(ris. 3.13). Na ris. 3.13 Solnce nahoditsya v
tochke ![]() , planeta -- v tochke
, planeta -- v tochke ![]() , os'
, os' ![]() napravlena v tochku
voshodyashego uzla orbity, a os'
napravlena v tochku
voshodyashego uzla orbity, a os' ![]() -- v tochku orbity, blizhaishei k Solncu, kotoraya nazyvaetsya
perigeliem. Ugol
-- v tochku orbity, blizhaishei k Solncu, kotoraya nazyvaetsya
perigeliem. Ugol ![]() nazyvaetsya
dolgotoi perigeliya.
nazyvaetsya
dolgotoi perigeliya.
Esli oboznachit' period obrasheniya planety ![]() kak
kak ![]() , to soglasno
vtoromu zakonu Keplera za vremya
, to soglasno
vtoromu zakonu Keplera za vremya ![]() planeta opishet polnyi ellips,
ploshad' kotorogo ravna
planeta opishet polnyi ellips,
ploshad' kotorogo ravna ![]() . Otnoshenie ploshadi ellipsa k
periodu obrasheniya ravno polovine uglovogo momenta planety, t.e.
. Otnoshenie ploshadi ellipsa k
periodu obrasheniya ravno polovine uglovogo momenta planety, t.e.
Tak kak
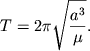
V sluchae, kogda na tela 1 i 2 ne deistvuyut sily prityazheniya drugih tel (v nebesnoi mehanike eta zadacha tak i nazyvaetsya zadachei dvuh tel), period obrasheniya est' velichina postoyannaya i mozhet sluzhit' edinicei vremeni. V nachale XX veka na osnove nablyudenii Solnca i Luny formirovalas' shkala efemeridnogo vremeni (Ephemeris Time, ET). Tak kak iz-za vozmushenii orbity drugimi telami period obrasheniya menyaetsya, dlya postroeniya shkaly ET neobhodimy byli dlitel'nye nablyudeniya. Iz-za slozhnosti postroeniya etoi shkaly, a takzhe iz-za poyavleniya v seredine 50-h godov XX veka atomnyh standartov chastoty ot shkaly vremeni, osnovannoi na obrashenii Zemli vokrug Solnca, prishlos' otkazat'sya. V nastoyashee vremya v osnove scheta vremeni lezhit atomnaya shkala vremeni TAI, odnako samoi stabil'noi na bol'shih intervalah vremeni mozhet okazat'sya pul'sarnaya shkala vremeni, prichem pul'sar yavlyaetsya odnoi iz zvezd v dvoinoi sisteme.
Oboznachim cherez ![]() srednyuyu skorost' dvizheniya planety:
srednyuyu skorost' dvizheniya planety:
V nebesnoi mehanike parametr
Analogichnoe uravnenie mozhno napisat' dlya drugoi planety s massoi
Uravnenie (3.51) yavlyaetsya matematicheskoi zapis'yu tret'ego zakona Keplera. Tak kak dlya samoi massivnoi planety v solnechnoi sisteme -- Yupitera otnoshenie
Kvadraty periodov obrasheniya planet otnosyatsya kak kuby ih bol'shih poluosei. Opredelyaya bol'shuyu poluos'
<< 3.10. Osnovy nebesnoi mehaniki | Oglavlenie | 3.10.2. Parametry i anomalii >>
|
Publikacii s klyuchevymi slovami:
astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |