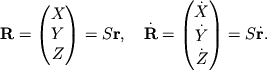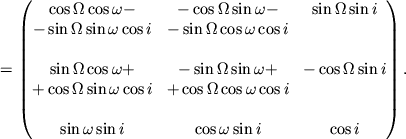3.10.2. Parametry i anomalii keplerovskoi orbity
Pri rassmotrenii dvizheniya planet mozhno ogranichit'sya tol'ko sluchaem ellipticheskogo dvizheniya. Orbita planety v etom sluchae harakterizuetsya shest'yu parametrami.
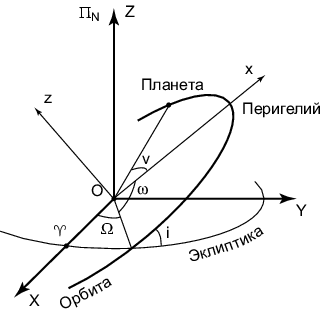
Opredelim sistemu koordinat ![]() , svyazannuyu s orbitoi planety.
Tochka orbity, blizhaishaya k Solncu, nazyvaetsya
perigeliem, a naibolee udalennaya ot Solnca --
afeliem. Os'
, svyazannuyu s orbitoi planety.
Tochka orbity, blizhaishaya k Solncu, nazyvaetsya
perigeliem, a naibolee udalennaya ot Solnca --
afeliem. Os' ![]() napravim v perigelii,
os'
napravim v perigelii,
os' ![]() -- perpendikulyarno ploskosti orbity. Tochki peresecheniya
ploskosti orbity planety i ekliptiki nazyvayutsya uzlami
orbity, prichem voshodyashim uzlom nazyvaetsya tot, kotoryi planeta
prohodit, perehodya iz oblasti otricatel'nyh shirot v oblast'
polozhitel'nyh shirot. Graficheskoe
predstavlenie i parametry keplerovskoi orbity pokazany na
ris. 3.14.
-- perpendikulyarno ploskosti orbity. Tochki peresecheniya
ploskosti orbity planety i ekliptiki nazyvayutsya uzlami
orbity, prichem voshodyashim uzlom nazyvaetsya tot, kotoryi planeta
prohodit, perehodya iz oblasti otricatel'nyh shirot v oblast'
polozhitel'nyh shirot. Graficheskoe
predstavlenie i parametry keplerovskoi orbity pokazany na
ris. 3.14.
Orientaciya orbity v prostranstve (orientaciya sistemy koordinat
![]() otnositel'no geliocentricheskoi sistemy
otnositel'no geliocentricheskoi sistemy ![]() )
opisyvaetsya tremya uglami. Ugol mezhdu napravleniem na tochku
vesennego ravnodenstviya i tochku voshodyashego uzla nazyvaetsya
dolgotoi voshodyashego uzla i oboznachaetsya
)
opisyvaetsya tremya uglami. Ugol mezhdu napravleniem na tochku
vesennego ravnodenstviya i tochku voshodyashego uzla nazyvaetsya
dolgotoi voshodyashego uzla i oboznachaetsya
![]() . Dvugrannyi ugol mezhdu
ploskostyami orbity i ekliptiki nazyvaetsya nakloneniem
orbity i oboznachaetsya kak
. Dvugrannyi ugol mezhdu
ploskostyami orbity i ekliptiki nazyvaetsya nakloneniem
orbity i oboznachaetsya kak ![]() . Tret'im
uglom, kotoryi oboznachaetsya
. Tret'im
uglom, kotoryi oboznachaetsya ![]() i nazyvaetsya
argumentom perigeliya, yavlyaetsya ugol mezhdu
napravleniyami na voshodyashii uzel i perigelii. Tak kak ugol
i nazyvaetsya
argumentom perigeliya, yavlyaetsya ugol mezhdu
napravleniyami na voshodyashii uzel i perigelii. Tak kak ugol ![]() postoyanen, to eto oznachaet
neizmennost' polozheniya osi
postoyanen, to eto oznachaet
neizmennost' polozheniya osi ![]() i v ploskosti orbity, i v
prostranstve.
i v ploskosti orbity, i v
prostranstve.
Sleduyushie dva parametra: bol'shaya poluos' ![]() i ekscentrisitet
i ekscentrisitet ![]() opredelyayut razmery i formu
orbity. I, nakonec,
polozhenie tela na orbite v nachal'nyi moment opredelyaetsya
epohoi prohozhdeniya cherez perigelii
--
opredelyayut razmery i formu
orbity. I, nakonec,
polozhenie tela na orbite v nachal'nyi moment opredelyaetsya
epohoi prohozhdeniya cherez perigelii
-- ![]() .
.
Mgnovennoe polozhenie planety na moment ![]() opredelyaetsya uglom
opredelyaetsya uglom
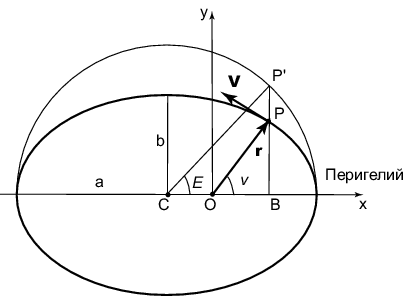
![]() , kotoryi nazyvaetsya istinnoi
anomaliei (ris. 3.15).
, kotoryi nazyvaetsya istinnoi
anomaliei (ris. 3.15).
Pomimo istinnoi anomalii v nebesnoi mehanike ispol'zuyutsya
ekscentricheskaya ![]() i
srednyaya
i
srednyaya ![]() anomalii. Postroim
okruzhnost' radiusa
anomalii. Postroim
okruzhnost' radiusa ![]() , ravnym bol'shoi poluosi ellipsa, s
centrom, kotoryi sovpadaet s centrom ellipsa
, ravnym bol'shoi poluosi ellipsa, s
centrom, kotoryi sovpadaet s centrom ellipsa ![]() . Opustim
perpendikulyar
. Opustim
perpendikulyar ![]() na os'
na os' ![]() ; togda ego prodolzhenie peresechet
okruzhnost' v tochke
; togda ego prodolzhenie peresechet
okruzhnost' v tochke ![]() . Ugol
. Ugol
![]() nazyvaetsya
ekscentricheskoi anomaliei. Ugol, ravnyi srednei anomalii,
opredelyaetsya srednim dvizheniem i raven
nazyvaetsya
ekscentricheskoi anomaliei. Ugol, ravnyi srednei anomalii,
opredelyaetsya srednim dvizheniem i raven
Chasto v nebesnoi mehanike i astrometrii ispol'zuetsya velichina, opredelyaemaya formuloi
i nazyvaemaya srednei dolgotoi.
Tak kak dvizhenie planety pri keplerovskom dvizhenii proishodit v
ploskosti, to polozhenie planety opredelyaetsya proekciyami
radius-vektora
![]() , kotorye ravny
, kotorye ravny ![]() . Proekciya
. Proekciya
![]() na os'
na os' ![]() ravna nulyu:
ravna nulyu:
![]() . Iz ris. 3.15
ochevidno, chto
. Iz ris. 3.15
ochevidno, chto
Takzhe, ispol'zuya ris. 3.15, nahodim, chto
Tak kak
Iz vyrazhenii (3.56), (3.57) i formuly tangensa polovinnogo ugla poluchim vyrazhenie, svyazyvayushee istinnuyu i ekscentricheskuyu anomalii:
Ugly
Teper' vernemsya k uravneniyu (3.42). Tak kak
![]() , to uravnenie (3.42) mozhno perepisat' v
vide:
, to uravnenie (3.42) mozhno perepisat' v
vide:
Zamenyaya
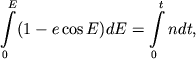
gde
Naidem teper' vektor skorosti
![]() . Zametim, chto
. Zametim, chto
![]() . Vektor skorosti lezhit v
ploskosti orbity, sledovatel'no, ego proekciya na os'
. Vektor skorosti lezhit v
ploskosti orbity, sledovatel'no, ego proekciya na os' ![]() ravna
nulyu. Iz (3.56) nahodim proekcii
ravna
nulyu. Iz (3.56) nahodim proekcii
![]() :
:
i kvadrat skorosti
Differenciruya po vremeni vektor skorosti (3.62) i uchityvaya,
chto
![]() , naidem vektor uskoreniya tela pri
dvizhenii po keplerovskoi orbite, kotoryi takzhe lezhit v ploskosti
orbity:
, naidem vektor uskoreniya tela pri
dvizhenii po keplerovskoi orbite, kotoryi takzhe lezhit v ploskosti
orbity:
Dlya vychisleniya pryamougol'nyh koordinat i proekcii skorosti tela v
geliocentricheskoi sisteme koordinat dostatochno naiti matricu
povorota ![]() sistemy
sistemy ![]() . Esli matrica
. Esli matrica ![]() izvestna, to
preobrazovanie zapisyvaetsya v vide matrichnyh uravnenii:
izvestna, to
preobrazovanie zapisyvaetsya v vide matrichnyh uravnenii:
Matrica ![]() vychislyaetsya sleduyushim obrazom (sm. ris. 3.14):
snachala vypolnyaem povorot otnositel'no osi
vychislyaetsya sleduyushim obrazom (sm. ris. 3.14):
snachala vypolnyaem povorot otnositel'no osi ![]() na ugol
na ugol ![]() do sovmesheniya osi
do sovmesheniya osi ![]() s liniei uzlov, zatem -- povorot
otnositel'no linii uzlov na ugol
s liniei uzlov, zatem -- povorot
otnositel'no linii uzlov na ugol ![]() i, nakonec, povorot
otnositel'no osi
i, nakonec, povorot
otnositel'no osi ![]() na ugol
na ugol ![]() :
:
Esli elementy orbity tela izvestny, to ego polozhenie i skorost' v
eklipticheskoi sisteme koordinat v lyuboi moment vremeni ![]() opredelyayutsya sleduyushei posledovatel'nost'yu vychislenii: 1) snachala
nahoditsya srednyaya anomaliya
opredelyayutsya sleduyushei posledovatel'nost'yu vychislenii: 1) snachala
nahoditsya srednyaya anomaliya ![]() po formule (3.53); 2) reshaya
uravnenie Keplera (3.61), nahodim ekscentricheskuyu anomaliyu
po formule (3.53); 2) reshaya
uravnenie Keplera (3.61), nahodim ekscentricheskuyu anomaliyu
![]() ; 3) znaya
; 3) znaya ![]() , poluchim radius-vektor tela
, poluchim radius-vektor tela
![]() (3.57) i ego proekcii
(3.57) i ego proekcii ![]() v orbital'noi sisteme
koordinat (3.56); 4) i, ispol'zuya uravneniya (3.65) i
matricu (3.66), poluchim pryamougol'nye eklipticheskie koordinaty
i proekcii skorosti tela.
v orbital'noi sisteme
koordinat (3.56); 4) i, ispol'zuya uravneniya (3.65) i
matricu (3.66), poluchim pryamougol'nye eklipticheskie koordinaty
i proekcii skorosti tela.
Esli ekscentrisitet orbity mal, to udobnym metodom resheniya
uravneniya Keplera yavlyaetsya metod iteracii. Na pervom shage
predpolagaetsya, chto ![]() . Togda process iteracii
. Togda process iteracii
Vyrazim teper' v vide ryada po stepenyam ekcentrisiteta ![]() istinnuyu anomaliyu
istinnuyu anomaliyu ![]() kak funkciyu srednei anomalii
kak funkciyu srednei anomalii ![]() . Dlya etogo
umnozhim snachala pervoe uravnenie (3.56) na
. Dlya etogo
umnozhim snachala pervoe uravnenie (3.56) na ![]() , vtoroe
-- na
, vtoroe
-- na ![]() i slozhim rezul'tat. Posle privedeniya podobnyh
chlenov poluchim:
i slozhim rezul'tat. Posle privedeniya podobnyh
chlenov poluchim:
Vyrazim teper'
![$\displaystyle \sin E=\sin(M+e\sin M+\frac{e^2}{2}\sin 2M) \approx \sin
M\Bigl[1-\frac{(e\sin M)^2}{2}\Bigr]+\frac{e}{2}\sin
2M+\frac{e^2}{2}\cos M\sin 2M.
$](https://images.astronet.ru/pubd/2003/06/11/0001190894/tex/formula912.gif)
Analogichno nahodim, chto
V zaklyuchenie etogo razdela rassmotrim dvizhenie Zemli po orbite.
1) Centr tyazhesti Zemli dvizhetsya otnositel'no centra mass sistemy
Zemlya+Luna. Poslednii nahoditsya na linii, soedinyayushei centry mass
Zemli i Luny, na rasstoyanii, ravnom
![]() km ot centra tyazhesti Zemli, gde
km ot centra tyazhesti Zemli, gde ![]() -- rasstoyanie mezhdu Zemlei i Lunoi, massy kotoryh ravny
-- rasstoyanie mezhdu Zemlei i Lunoi, massy kotoryh ravny
![]() .
.
2) Centr tyazhesti sistemy Zemlya+Luna dvizhetsya vokrug Solnca po
orbite, elementy kotoroi ne yavlyayutsya postoyannymi, a yavlyayutsya
funkciyami vremeni. Orbita blizka k krugovoi; ekscentrisitet
orbity raven
![]() . Orbita centra tyazhesti sistemy
Zemlya+Luna yavlyaetsya vozmushennoi vsledstvie prityazheniya
Zemli, Luny i Solnca planetami. Iz-za vozmushenii dvizhenie centra
tyazhesti sistemy Zemlya+Luna otlichaetsya ot keplerovskogo dvizheniya,
odnako eto otlichie ne prevyshaet v dolgote
. Orbita centra tyazhesti sistemy
Zemlya+Luna yavlyaetsya vozmushennoi vsledstvie prityazheniya
Zemli, Luny i Solnca planetami. Iz-za vozmushenii dvizhenie centra
tyazhesti sistemy Zemlya+Luna otlichaetsya ot keplerovskogo dvizheniya,
odnako eto otlichie ne prevyshaet v dolgote
![]() , v shirote
, v shirote
![]() .
.
3) Centr Solnca dvizhetsya otnositel'no centra tyazhesti solnechnoi
sistemy -- baricentra. Dvizhenie centra Solnca
otnositel'no baricentra solnechnoi sistemy opredelyaetsya, glavnym
obrazom, dvumya naibolee massivnymi planetami -- Yupiterom i
Saturnom i predstavlyaetsya dvumya pochti krugovymi dvizheniyami s
periodami obrasheniya etih planet (![]() i
i ![]() let).
Radius krugovyh dvizhenii centra Solnca otnositel'no baricentra
raven primerno
let).
Radius krugovyh dvizhenii centra Solnca otnositel'no baricentra
raven primerno
![]() dlya Yupitera i
dlya Yupitera i
![]() dlya Saturna (
dlya Saturna (![]() i
i ![]() --
otnosheniya massy Solnca k massam Yupitera i Saturna)
(ris. 3.16).
--
otnosheniya massy Solnca k massam Yupitera i Saturna)
(ris. 3.16).
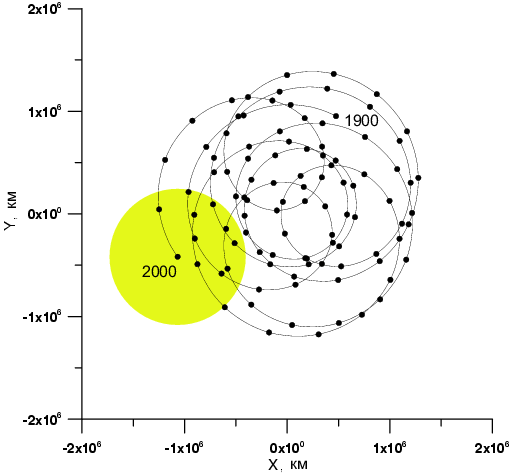 |
Ris. 3.16. Dvizhenie Solnca otnositel'no baricentra solnechnoi sistemy v eklipticheskoi sisteme koordinat na intervale vremeni 1900 -- 2000 gg. Promezhutok mezhdu tochkami raven odnomu godu. |
Orbital'nye skorosti dvizheniya Yupitera i Saturna ravny primerno 13
km/s i 9,5 km/s, sootvetstvenno komponenty skorosti dvizheniya
centra Solnca, vyzyvaemye etimi planetami, sostavlyayut
![]() ,
,
![]() .
.
<< 3.10.1. Zakony Keplera | Oglavlenie | 4. Sistemy koordinat na >>
|
Publikacii s klyuchevymi slovami:
astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |