Astronet > Sfericheskaya astronomiya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 1.2. Kratkii istoricheskii obzor | Oglavlenie | 2.2. Skalyary, vektory, tenzory >>

2. Osnovy sfericheskoi geometrii

Odnim iz glavnyh dostizhenii kosmicheskogo proekta HIPPARCOS, osushestvlennogo v 90-h godah XX veka, yavlyaetsya izmerenie parallaksov (ili rasstoyanii) do $\sim 120000$ zvezd, kotorye nahodyatsya na rasstoyanii do 1 kiloparseka (kpk) ot Solnca. Nesmotrya na to, chto ob'em, v kotorom raspolozheny eti zvezdy sostavlyaet ochen' maluyu chast' ot ob'ema nashei Galaktiki, izmerenie rasstoyanii yavlyaetsya vazhneishim rezul'tatom proekta, potomu chto okazalos' vozmozhnym postroit' trehmernuyu kartinu blizhaishei okrestnosti Solnca.

Esli rasstoyaniya do nebesnyh ob'ektov neizvestny, to udobno otnesti vse ob'ekty: zvezdy, radioistochniki i t.d. na odno i to zhe rasstoyanie, to est' raspolozhit' ih na poverhnosti sfery s centrom v tochke, gde nahoditsya nablyudatel'. Takaya sfera nazyvaetsya nebesnoi sferoi. Radius nebesnoi sfery proizvolen, no udobno dlya dal'neishih vychislenii schitat' ego ravnym edinice.

Chtoby znat' izmenenie polozheniya zvezdy v prostranstve, neobhodimo izmerit' tri komponenty skorosti zvezdy. K sozhaleniyu dlya bol'shinstva zvezd izvestny lish' dve komponenty skorosti v kartinnoi ploskosti, to est' v ploskosti, perpendikulyarnoi linii, soedinyayushei nablyudatelya i zvezdu. Udobnee vsego schitat', chto kartinnaya ploskost' sovpadaet s ploskost'yu, kasatel'noi k nebesnoi sfere.

Geometricheskie postroeniya i vychisleniya na poverhnosti sfery otlichayutsya ot takovyh na ploskosti. Poetomu mozhno govorit' o sfericheskoi geometrii kak o samostoyatel'nom razdele geometrii. Sleduet zametit', chto formuly sfericheskoi geometrii spravedlivy ne tol'ko dlya nebesnoi sfery, no i dlya lyuboi drugoi sfery (naprimer, pri provedenii vychislenii na zemnom globuse). Neobhodimo lish' uchityvat' radius sfery.

Odnimi iz osnovnyh ponyatii planimetrii yavlyayutsya ponyatiya tochki i pryamoi linii. V sfericheskoi geometrii analogom pryamoi linii kak linii s naimen'shei dlinoi, soedinyayushei dve tochki, yavlyaetsya duga okruzhnosti, obrazovannoi peresecheniem bol'shogo kruga s nebesnoi sferoi. Tak kak krug -- eto chast' ploskosti, ogranichennaya okruzhnost'yu, to dadim sleduyushee opredelenie.

Opredelenie 2.1.1 Bol'shim krugom nazyvaetsya chast' ploskosti, kotoraya prohodit cherez centr sfery.

Opredelenie 2.1.2 Lyubaya ploskost', kotoraya ne prohodit cherez centr sfery, nazyvaetsya malym krugom.

Cherez lyubye dve tochki, lezhashie na poverhnosti sfery, mozhno provesti bol'shoi krug. Eto utverzhdenie ekvivalentno aksiome iz planimetrii: cherez lyubye dve tochki mozhno provesti pryamuyu liniyu. Perpendikulyar k bol'shomu krugu, prohodyashii cherez centr sfery, peresekaet ee v dvuh tochkah, nazyvaemyh polyusami. Bol'shoi krug peresekaet sferu po okruzhnosti. Ochevidno, chto lyubaya pryamaya, lezhashaya v ploskosti bol'shogo kruga i prohodyashaya cherez centr sfery, yavlyaetsya diametrom sfery. Sledovatel'no, dva bol'shih kruga peresekayutsya po diametru sfery.

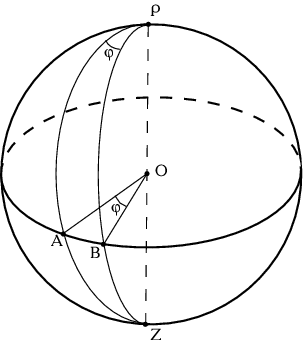
Rassmotrim sferu s centrom v tochke $O$ (ris. 2.1).

Ris. 2.1. Opredelenie dvugrannogo ugla

Provedem bol'shoi krug cherez dve tochki $A$ i $B$ , lezhashie na poverhnosti sfery, zatem provedem perpendikulyar k bol'shomu krugu. Polyusy oboznachim kak $P$ i $Z$ . Cherez tochki $P$ i $A$ , zatem cherez $P$ i $B$ provedem dva bol'shih kruga.

Opredelenie 2.1.3 Ugol mezhdu ploskostyami dvuh bol'shih krugov nazyvaetsya dvugrannym uglom.

Edinicami izmereniya uglov v astronomii yavlyayutsya gradusy, radiany, chasy. Tak kak radius sfery raven edinice, to dlina dugi $\widehat{AB}$ (ris. 2.1) ravna central'nomu uglu $AOB$ , to est' $\varphi$ , vyrazhennomu v radianah. Po opredeleniyu gradus $(^\circ)$ -- eto central'nyi ugol, ravnyi $1/360$ chasti okruzhnosti. Gradus delitsya na 60 uglovyh minut $(1^\circ = 60')$ , kazhdaya iz kotoryh ravna 60 uglovym sekundam $(1'=60\hbox{$^{\prime\prime}$})$ , to est' gradus sostoit iz 3600 uglovyh sekund $(1^\circ = 3600\hbox{$^{\prime\prime}$})$ .

Dlina okruzhnosti ravna $2\pi$ radian, poetomu

$\displaystyle 1\$ radian $\displaystyle = \frac{360^\circ}{2\pi} \approx 57\hbox{$^{\circ}$\kern-.15cm{,}\kern.04cm}29577951308232\approx 206264\hbox{$^{\prime\prime}$\kern-.15cm{,}\kern.04cm}80624709636.$

V sovremennyh astrometricheskih nablyudeniyah tochnost' namnogo prevyshaet $1\hbox{$^{\prime\prime}$}$ . Poetomu chasto v kachestve edinicy izmereniya uglov ispol'zuetsya millisekunda (ms) dugi, prichem $1\$ ms dugi $= 10^{-3}\hbox{$^{\prime\prime}$}$ . Chtoby predstavit' sebe velichinu ugla v 1 ms dugi, vychislim uglovoi razmer goroshiny diametrom 5 mm, nahodyasheisya na rasstoyanii, ravnom 1000 km. Uglovoi razmer goroshiny raven:

$\displaystyle \frac{5\cdot 10^{-3}\ \textrm{m}}{10^6\ \textrm{m}}\times 206264\hbox{$^{\prime\prime}$\kern-.15cm{,}\kern.04cm}8062 \approx 10^{-3}\hbox{$^{\prime\prime}$}.$

Dlya izmereniya uglov ispol'zuyutsya takzhe chasy, prichem $(1^h)$ -- eto central'nyi ugol, sootvetstvuyushii $1/24$ chasti okruzhnosti. V odnom chase soderzhitsya 60 minut ili 3600 sekund $(1^h = 60^m =3600^s)$ . Ochevidno, chto $1^h = 15^\circ, 1^m =15', 1^s=15\hbox{$^{\prime\prime}$}$ .

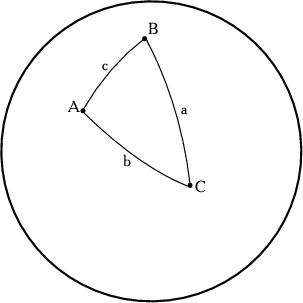
Rassmotrim teper' tri tochki, kotorye lezhat na sfere i ne prinadlezhat odnomu bol'shomu krugu. Cherez kazhduyu paru tochek mozhno provesti bol'shie krugi (ris. 2.2).

Ris. 2.2. Opredelenie sfericheskogo treugol'nika

Opredelenie 2.1.4 Sfericheskim treugol'nikom nazyvaetsya figura, obrazovannaya tremya dugami okruzhnostei bol'shih krugov, poparno soedinyayushih tri tochki.

Primerami sfericheskih treugol'nikov mogut byt' treugol'niki $ABP$ , $ABZ$ (ris. 2.1) i $ABC$ (ris. 2.2).

Obychno ugly sfericheskogo treugol'nika oboznachayut bol'shimi bukvami, naprimer $A,B,C$ , a storony, protivolezhashie uglam -- sootvetstvuyushimi malymi bukvami: $AB=c, BC=a, AC=b$ (ris. 2.2). Kak i v planimetrii, v sfericheskoi geometrii sushestvuyut opredelennye sootnosheniya mezhdu storonami i uglami treugol'nikov. Osnovnye formuly, svyazyvayushie ugly i storony treugol'nika, budut vyvedeny v sleduyushem paragrafe. Zdes' otmetim lish' sleduyushie svoistva sfericheskih treugol'nikov. Ugly $A$ i $B$ v treugol'nike $ABP$ (ris. 2.1) - pryamye, tak kak bol'shie krugi, prohodyashie cherez tochki $P,A,Z$ i $P,B,Z$ , perpendikulyarny ploskosti $AOB$ . Poetomu, poskol'ku ugol $\varphi\gt 0$ , summa uglov sfericheskogo treugol'nika mozhet prevyshat' $180^\circ$ . Teper' provedem ploskost' cherez tochki $A,B,C$ (ris. 2.2), lezhashie na sfere, i parallel'no ei ploskost', kotoraya prohodit cherez centr sfery. Ochevidno, chto eta ploskost' podelit sferu na dve polusfery, prichem treugol'nik $ABC$ budet polnost'yu lezhat' v odnoi iz polusfer. Takim obrazom, lyuboi iz uglov sfericheskogo treugol'nika budet men'she, chem $180^\circ$ . V predele (pri uvelichenii kazhdogo iz uglov do $180^\circ$ ) sfericheskii treugol'nik transformiruetsya v polusferu.

Sleduyushie svoistva sfericheskogo treugol'nika analogichny svoistvam ploskogo treugol'nika:
a) V kazhdom sfericheskom treugol'nike protiv bol'shego ugla lezhit bol'shaya storona;
b) Summa lyubyh dvuh storon bol'she tret'ei storony.

Naidem ploshad' sfericheskogo treugol'nika. Dlya etogo rassmotrim treugol'nik $ABC$ (ris. 2.3).

Ris. 2.3. Vychislenie ploshadi sfericheskogo treugol'nika

Oboznachim ego ploshad' cherez $S$ . Ploskost' $ABMA'B'N$ delit sferu na dve polusfery, v odnoi iz kotoryh i raspolozhen treugol'nik $ABC$ . Ploshad' polusfery ravna $2\pi R^2$ , esli radius sfery raven $R$ . Na ris. 2.3 ploshad' blizhnei k nam polusfery skladyvaetsya iz ploshadei sleduyushih figur: segmenta sfery $ABMA'CA$ , segmenta $BCB'NAB$ minus treugol'nik $ABC$ , segmenta $CA'C'B'C$ minus treugol'nik $A'B'C'$ . Esli ugly treugol'nika $ABC$ izmeryayutsya v radianah, to ploshad' kazhdogo iz ukazannyh segmentov ravna $2AR^2$ , $2BR^2$ , $2CR^2$ , sootvetstvenno. Treugol'nik $A'B'C'$ ravnovelik zadannomu treugol'niku $ABC$ . Poetomu mozhno napisat' uravnenie:

$\displaystyle 2\pi R^2 = 2AR^2+ 2BR^2-S+ 2CR^2-S.$

Otsyuda ploshad' sfericheskogo treugol'nika $ABC$ ravna

$\displaystyle S=R^2(A+B+C-\pi),$

gde ugly $A,B,C$ vyrazheny v radianah.

Opredelim teper' ploshad' vsei nebesnoi sfery. Dlya etogo udobno ploshad' sfery vyrazit' v kvadratnyh gradusah. Dlya etogo snachala vyrazim radius sfery v gradusah: $R=360^\circ/2\pi$ . Togda ploshad' vsei sfery ravna

$\displaystyle 4\pi R^2=4\pi\left(\frac{360^\circ}{2\pi}\right)^2\approx 41252.97$ kvadratnyh gradusov $\displaystyle .$

<< 1.2. Kratkii istoricheskii obzor | Oglavlenie | 2.2. Skalyary, vektory, tenzory >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni

Sm. takzhe:

Dostizheniya kosmicheskoi astrometrii

Skonchalsya Konstantin Vladislavovich Kuimov

Konstantinu Vladislavovichu Kuimovu – 75 let

Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya.

Vrashenie Zemli i prodolzhitel'nost' sutok

80 let so dnya rozhdeniya Al'berta Petrovicha Gulyaeva

Rukovodstvo po prakticheskoi rabote s katalogom Hipparcos

Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

2. Osnovy sfericheskoi geometrii

Razdely

2.1. Osnovnye ponyatiya