Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu << A.2 Lineinaya algebra | Oglavlenie | A.4 Elementy differencial'nogo i >>

A.3 Dekartovy pryamougol'nye i sfericheskie koordinaty vektora

Esli bazisnye vektory ili orty $ {\mathbf{i}},{\mathbf{j}}, {\mathbf{k}}$ vzaimno perpendikulyarny i opredelyayut osi sistemy koordinat $ Ox, Oy, Oz$, to razlozhenie

$\displaystyle {\mathbf{u}} = u_x{\mathbf{i}}+u_y{\mathbf{j}}+ u_z{\mathbf{e}} $

opredelyaet dekartovy pryamougol'nye koordinaty $ u_x,u_y,u_z$ vektora $ {\mathbf{u}}$.

Bazisnymi vektorami sfericheskoi sistemy koordinat yavlyaetsya troika edinichnyh vektorov $ {\mathbf{i}}_r,{\mathbf{i}}_\theta, {\mathbf{i}}_\lambda$, napravlennyh v storonu uvelicheniya sootvetstvuyushih koordinat: $ r$ -- rasstoyaniya, $ \theta$ -- koshiroty, $ \lambda$ -- dolgoty. Razlozhenie vektora $ {\mathbf{u}}$ po bazisu imeet vid:

$\displaystyle {\mathbf{u}}=u_r{\mathbf{i}}_r+u_\theta{\mathbf{i}}_\theta+ u_\lambda{\mathbf{i}}_\lambda, $

$ u_r,u_\theta,u_\lambda$ komponenty vektora $ {\mathbf{u}}$ v bazise $ {\mathbf{i}}_r,{\mathbf{i}}_\theta, {\mathbf{i}}_\lambda$.

Dekartovy koordinaty vektora $ {\mathbf{u}}=(u_x,u_y,u_z)$ vyrazhayutsya cherez sfericheskie koordinaty $ (r,\theta,\lambda)$ sleduyushim obrazom:

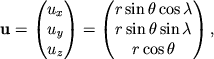
$\displaystyle {\mathbf{u}}= \begin{pmatrix} u_x \\ u_y \\ u_z \end{pmatrix} = \begin{pmatrix} r\sin\theta\cos\lambda \\ r\sin\theta\sin\lambda \\ r\cos\theta \end{pmatrix}, $

$ r=\vert{\mathbf{u}}\vert$.

Edinichnye vektory $ {\mathbf{i}}_r,{\mathbf{i}}_\theta, {\mathbf{i}}_\lambda$ v dekartovyh koordinatah imeyut vid:

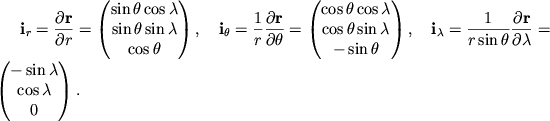
$\displaystyle {\mathbf{i}}_r=\frac{\partial{\mathbf{r}}}{\partial{r}}= \begin{pmatrix} \sin\theta\cos\lambda \\ \sin\theta\sin\lambda \\ \cos\theta \end{pmatrix}, \quad {\mathbf{i}}_\theta=\frac{1}{r}\frac{\partial{\mathbf{r}}}{\partial{\theta}}= \begin{pmatrix} \cos\theta\cos\lambda \\ \cos\theta\sin\lambda \\ -\sin\theta \end{pmatrix}, \quad {\mathbf{i}}_\lambda=\frac{1}{r\sin\theta}\frac{\partial{\mathbf{r}}}{\partial{\lambda}}= \begin{pmatrix} -\sin\lambda \\ \cos\lambda \\ 0 \end{pmatrix}. $

Preobrazovanie mezhdu komponentami vektora v dekartovom i sfericheskom bazise imeet vid:

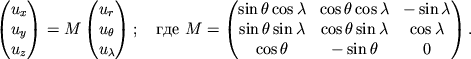
$\displaystyle \begin{pmatrix} u_x \\ u_y \\ u_z \end{pmatrix} = M \begin{pmatrix} u_r \\ u_\theta \\ u_\lambda \end{pmatrix}; \quad \textrm{gde}\ M = \begin{pmatrix} \sin\theta\cos\lambda & \cos\theta\cos\lambda & -\sin\lambda\\ \sin\theta\sin\lambda & \cos\theta\sin\lambda & \cos\lambda\\ \cos\theta & -\sin\theta & 0 \end{pmatrix}. $

Obratnoe preobrazovanie imeet vid:

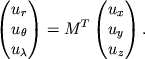
$\displaystyle \begin{pmatrix} u_r \\ u_\theta \\ u_\lambda \end{pmatrix} = M^T \begin{pmatrix} u_x \\ u_y \\ u_z \end{pmatrix}. $


<< A.2 Lineinaya algebra | Oglavlenie | A.4 Elementy differencial'nogo i >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]
Ocenka: 3.5 [golosov: 304]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya