Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu << A.3 Dekartovy pryamougol'nye i | Oglavlenie | A.5 Krivolineinye koordinaty >>

A.4 Elementy differencial'nogo i integral'nogo ischisleniya

Differencial funkcii $ y=f(x)$ v tochke $ x$, esli on sushestvuet, raven:

$\displaystyle dy = \frac{dy}{dx}dx=f'(x)dx, $

$ f'(x)=dy/dx$ -- proizvodnaya funkcii.

Differencial funkcii $ y=f(x_1,x_2,\ldots,x_n)$, esli on sushestvuet, raven:

$\displaystyle dy = \frac{\partial{f}}{\partial{x}_1}dx_1+\frac{\partial{f}}{\partial{x}_2}dx_2+\ldots+ \frac{\partial{f}}{\partial{x}_n}dx_n, $

prichem chastnye proizvodnye $ \frac{\partial{f}}{dx_1},\ldots,\frac{\partial{f}}{dx_n}$ vychislyayutsya v rassmatrivaemoi tochke.

Esli $ f(x)$ -- deistvitel'naya funkciya, imeyushaya v intervale $ a\leq x \lt b$ $ n$-uyu proizvodnuyu $ f^{(n)}$, to

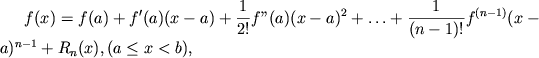
$\displaystyle f(x)=f(a)+f'(a)(x-a)+\frac{1}{2!}f

gde $ R_n(x)$ nazyvaetsya ostatochnym chlenom.

Gradientom skalyarnoi funkcii $ F({\mathbf{r}})=F(x,y,z)$ nazyvaetsya vektornaya funkciya, opredelyaemaya formuloi:

$\displaystyle \textrm{grad}\ F({\mathbf{r}})$ $\displaystyle = \frac{\partial{F}}{\partial{x}}{\mathbf{i}} + \frac{\partial{F}}{\partial{y}}{\mathbf{j}} + \frac{\partial{F}}{\partial{z}}{\mathbf{k}}$ $\displaystyle \textrm{v dekartovyh koordinatah},$    
$\displaystyle \textrm{grad}\ F({\mathbf{r}})$ $\displaystyle = \frac{\partial{F}}{\partial{r}}{\mathbf{i}}_r + \frac{1}{r}\frac{\partial{F}}{\partial{\theta}}{\mathbf{i}}_\theta + \frac{1}{r\sin\theta}\frac{\partial{F}}{\partial{\lambda}}{\mathbf{i}}_\lambda$ $\displaystyle \textrm{v sfericheskih koordinatah}.$    

Polnyi differencial $ dF$ skalyarnoi funkcii $ F({\mathbf{r}})=F(x,y,z)$, sootvetstvuyushii peremesheniyu tochki na $ d{\mathbf{r}} = dx\,{\mathbf{i}} + dy\,{\mathbf{j}} + dz\,{\mathbf{k}}$ raven:

$\displaystyle dF({\mathbf{r}}) = \frac{\partial{F}}{\partial{x}}dx + \frac{\partial{F}}{\partial{y}}dy + \frac{\partial{F}}{\partial{z}}dx = d{\mathbf{r}}\cdot \textrm{grad}\ F({\mathbf{r}}). $

Differencial $ d{\mathbf{r}}$ radius-vektora $ {\mathbf{r}}$ vdol' krivoi $ C$, opisyvaemoi uravneniem

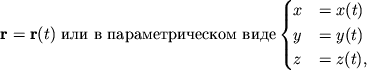
\begin{displaymath} {\mathbf{r}}={\mathbf{r}}(t)\ \textrm{ili v parametricheskom vide} \begin{cases} x &=x(t) \\ y &=y(t) \\ z &=z(t), \end{cases}\end{displaymath}

opredelyaetsya v kazhdoi tochke $ {\mathbf{r}}=\Bigl(x(t),y(t),z(t)\Bigr)$ krivoi formuloi:

$\displaystyle d{\mathbf{r}} = dx\,{\mathbf{i}} + dy\,{\mathbf{j}} + dz\,{\mathbf{k}} =\Bigl( \frac{dx}{dt}{\mathbf{i}} + \frac{dy}{dt}{\mathbf{j}} + \frac{dz}{dt}{\mathbf{k}}\Bigr)dt. $

Vektor $ d{\mathbf{r}}$ napravlen po kasatel'noi k krivoi $ C$ v tochke s radius-vektorom $ {\mathbf{r}}$.

Kvadrat elementa dliny raven

$\displaystyle ds^2$ $\displaystyle = dx^2+dy^2+dz^2$ $\displaystyle \textrm{v dekartovyh koordinatah},$    
$\displaystyle ds^2$ $\displaystyle = dr^2+r^2d\theta^2+r^2\sin^2\theta\, d\lambda^2$ $\displaystyle \textrm{v sfericheskih koordinatah}.$    

Preobrazovanie differencialov iz sfericheskoi v dekartovu sistemu koordinat imeet vid:

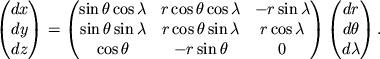
$\displaystyle \begin{pmatrix} dx \\ dy \\ dz \end{pmatrix} = \begin{pmatrix} \sin\theta\cos\lambda & r\cos\theta\cos\lambda & -r\sin\lambda\\ \sin\theta\sin\lambda & r\cos\theta\sin\lambda & r\cos\lambda\\ \cos\theta & -r\sin\theta & 0 \end{pmatrix}\begin{pmatrix} dr \\ d\theta \\ d\lambda \end{pmatrix}. $


<< A.3 Dekartovy pryamougol'nye i | Oglavlenie | A.5 Krivolineinye koordinaty >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]
Ocenka: 3.5 [golosov: 304]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya