Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu << A.4 Elementy differencial'nogo i | Oglavlenie | A.6 Sfericheskie funkcii >>

A.5 Krivolineinye koordinaty

Esli v oblasti $ V$ trehmernogo evklidova prostranstva zadany sootnosheniya, stavyashie v sootvetstvie kazhdoi tochke $ (x,y,z)$ troiku chisel $ x^i,\ i=1,2,3$, prichem

$\displaystyle x^1=f_1(x,y,z), \quad x^2=f_2(x,y,z), \quad x^3=f_3(x,y,z), $

to funkcii $ x^1, x^2, x^3$ nazyvayutsya krivolineinymi koordinatami tochki.

Uslovie $ x^i=f_i(x,y,z)=\textrm{const},\ i=1,2,3$ opredelyaet koordinatnuyu poverhnost'. Dve koordinatnyh poverhnosti, sootvetstvuyushie razlichnym koordinatam $ x^i, x^j, (i\neq j)$ peresekayutsya po koordinatnoi linii, sootvetstvuyushei tret'ei koordinate $ x^k$.

Edinichnye vektory $ {\mathbf{i}}_1(x^1,x^2,x^3), {\mathbf{i}}_2(x^1,x^2,x^3), {\mathbf{i}}_3(x^1,x^2,x^3)$ kasatel'nye k koordinatnym liniyam $ x^1, x^2, x^3$ yavlyayutsya lokal'nymi bazisnymi vektorami.

V kachestve lokal'nyh bazisnyh vektorov mozhno vybrat' troiku vektorov (ne obyazatel'no edinichnyh), kotorye opredelyayutsya uravneniyami:

$\displaystyle {\mathbf{e}}_1(x^1,x^2,x^3)=\sqrt{g_{11}}\,{\mathbf{i}}_1, \quad {\mathbf{e}}_2(x^1,x^2,x^3)=\sqrt{g_{22}}\,{\mathbf{i}}_2, \quad {\mathbf{e}}_2(x^1,x^2,x^3)=\sqrt{g_{33}}\,{\mathbf{i}}_3, $

napravlennyh po koordinatnym liniyam, gde $ g_{ii}$ -- komponenty metricheskogo tenzora:

$\displaystyle g_{ik}(x^1,x^2,x^3)=\left.\Bigl(\frac{\partial{x}}{\partial{x}^i}\frac{\partial{x}}{\partial{x}^k} + \frac{\partial{y}}{\partial{x}^i}\frac{\partial{y}}{\partial{x}^k} + \frac{\partial{z}}{\partial{x}^i}\frac{\partial{z}}{\partial{x}^k}\Bigr)\right\vert _{(x^1,x^2,x^3)}. $

Lokal'nye bazisnye vektory $ {\mathbf{e}}_1,{\mathbf{e}}_2, {\mathbf{e}}_3$ mogut byt' vyrazheny cherez orty $ {\mathbf{i}},{\mathbf{j}}, {\mathbf{k}}$ dekartovoi sistemy koordinat po formulam:

$\displaystyle {\mathbf{e}}_i = \frac{\partial{x}}{\partial{x}^i}{\mathbf{i}} + \frac{\partial{y}}{\partial{x}^i}{\mathbf{j}} + \frac{\partial{z}}{\partial{x}^i}{\mathbf{k}}. $

Funkcii $ \frac{\partial{x}}{\partial{x}^i}, \frac{\partial{y}}{\partial{x}^i}, \frac{\partial{z}}{\partial{x}^i}$ yavlyayutsya napravlyayushimi kosinusami orta $ {\mathbf{e}}_i$ po otnosheniyu k dekartovym osyam $ Ox, Oy, Oz$.

V kachestve lokal'nyh bazisnyh vektorov mozhno vybrat' troiku vektorov $ {\mathbf{e}}^1, {\mathbf{e}}^2, {\mathbf{e}}^3$:

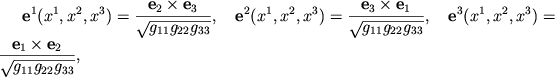
$\displaystyle {\mathbf{e}}^1(x^1,x^2,x^3)=\frac{{\mathbf{e}}_2\times {\mathbf{e}}_3} {\sqrt{g_{11}g_{22}g_{33}}}, \quad {\mathbf{e}}^2(x^1,x^2,x^3)=\frac{{\mathbf{e}}_3\times {\mathbf{e}}_1} {\sqrt{g_{11}g_{22}g_{33}}}, \quad {\mathbf{e}}^3(x^1,x^2,x^3)=\frac{{\mathbf{e}}_1\times {\mathbf{e}}_2} {\sqrt{g_{11}g_{22}g_{33}}}, $

napravlennyh perpendikulyarno k koordinatnym poverhnostyam.

V bazise $ {\mathbf{e}}_1,{\mathbf{e}}_2, {\mathbf{e}}_3$ koordinaty vektora $ \mathbf{a}$ nazyvayutsya kovariantnymi koordinatami:

$\displaystyle a_i = a_i(x^1,x^2,x^3)={\mathbf{a}}\cdot{\mathbf{e}}_i,\ i=1,2,3, $

a v bazise $ {\mathbf{e}}^1, {\mathbf{e}}^2, {\mathbf{e}}^3$ -- kontravariantnymi:

$\displaystyle a^i = a^i(x^1,x^2,x^3)={\mathbf{a}}\cdot{\mathbf{e}}^i,\ i=1,2,3. $

Spravedlivy formuly:

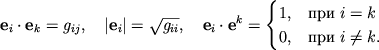
$\displaystyle {\mathbf{e}}_i\cdot {\mathbf{e}}_k=g_{ij}, \quad \vert{\mathbf{e}}_i\vert = \sqrt{g_{ii}}, \quad {\mathbf{e}}_i\cdot {\mathbf{e}}^k= \begin{cases} 1,& \textrm{pri}\ i=k\\ 0,& \textrm{pri}\ i\neq k. \end{cases}$

V chastnom sluchae pryamougol'nyh dekartovyh koordinat $ x^1=x, x^2=y, x^3=z$ imeem:

$\displaystyle {\mathbf{e}}_1={\mathbf{e}}^1={\mathbf{i}}_1={\mathbf{i}}, \quad {\mathbf{e}}_2={\mathbf{e}}^2={\mathbf{i}}_2={\mathbf{j}}, \quad {\mathbf{e}}_3={\mathbf{e}}^3={\mathbf{i}}_3={\mathbf{k}}. $

Sistema krivolineinyh koordinat $ x^1, x^2, x^3$ yavlyaetsya ortogonal'noi, esli

$\displaystyle g_{ik}(x^1,x^2,x^3)=0\ \textrm{pri}\ i\neq k $

v kazhdoi tochke $ (x^1, x^2, x^3)$. Koordinatnye linii, a znachit, i vektory lokal'nogo bazisa $ {\mathbf{i}}_1, {\mathbf{i}}_2, {\mathbf{i}}_3$ budut perpendikulyarny drug k drugu v kazhdoi tochke.

Element ob'ema $ dV$ v krivolineinyh koordinatah raven:

$\displaystyle dV = \sqrt{g}\,dx^1dx^2dx^3,\ \sqrt{g}= \sqrt{g_{11}g_{22}g_{33}}\,. $

Integral po ob'emu ot funkcii $ f(x,y,z)=f[x(x^1,x^2,x^3), y(x^1,x^2,x^3), z(x^1,x^2,x^3)]$ po ogranichennoi oblasti $ V$ raven

$\displaystyle \int_V f(x,y,z)dV$ $\displaystyle = \iiint_V f(x,y,z)dx dy dz =$    
$\displaystyle =\iiint_V f[x(x^1,x^2,x^3), y(x^1,x^2,x^3), z(x^1,x^2,x^3)] \sqrt{g}dx^1dx^2dx^3.$    

Integral po ob'emu ne zavisit ot vybora sistemy koordinat i mozhet byt' vyrazhen neposredstvenno cherez troinye integraly po $ x,y,z$ ili $ x^1, x^2, x^3$.

V sfericheskih koordinatah $ \sqrt{g}=r^2\sin\theta$.


<< A.4 Elementy differencial'nogo i | Oglavlenie | A.6 Sfericheskie funkcii >>

Publikacii s klyuchevymi slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [13]
Ocenka: 3.5 [golosov: 304]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya