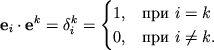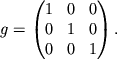2.3. Sfericheskaya sistema koordinat
Dlya resheniya mnogih zadach okazyvaetsya udobnee vmesto dekartovoi
sistemy ispol'zovat' krivolineinye sistemy koordinat. V obshem
sluchae ispol'zuyutsya tri funkcii
![]() ,
,
![]() ,
,
![]() dlya opredeleniya polozheniya tela v prostranstve.
Koordinatnaya setka sostoit iz peresekayushihsya krivyh
dlya opredeleniya polozheniya tela v prostranstve.
Koordinatnaya setka sostoit iz peresekayushihsya krivyh
![]() vmesto setki pryamyh linii
vmesto setki pryamyh linii
![]() v
dekartovoi sisteme. Esli funkcii vybrany podhodyashim obrazom, to
polozhenie ob'ekta mozhet byt' odnoznachno opredeleno s
pomosh'yu krivolineinyh koordinat
v
dekartovoi sisteme. Esli funkcii vybrany podhodyashim obrazom, to
polozhenie ob'ekta mozhet byt' odnoznachno opredeleno s
pomosh'yu krivolineinyh koordinat
![]() vmesto dekartovyh
koordinat
vmesto dekartovyh
koordinat ![]() .
.
K takim sistemam otnositsya i sfericheskaya sistema
koordinat, shiroko
ispol'zuemaya ne tol'ko v astronomii, no i drugih naukah.
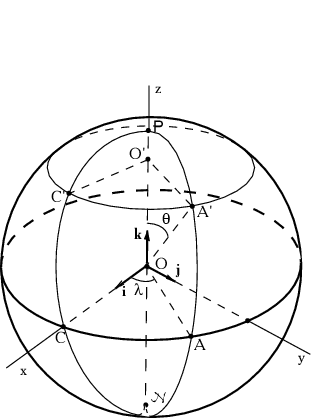
Sfericheskie koordinaty (sm. ris. 2.5): ![]() --
radius-vektor ob'ekta,
--
radius-vektor ob'ekta, ![]() -- polyarnoe
rasstoyanie, kotoroe inogda nazyvayut
koshirotoi, i
-- polyarnoe
rasstoyanie, kotoroe inogda nazyvayut
koshirotoi, i ![]() -- dolgota svyazany s dekartovymi koordinatami
-- dolgota svyazany s dekartovymi koordinatami
![]() uravneniyami:
uravneniyami:
Polyarnoe rasstoyanie izmenyaetsya ot
Sistema uravnenii (2.20) predstavlyaet preobrazovanie mezhdu
sfericheskoi i dekartovoi sistemami koordinat. Sledovatel'no,
funkcii
![]() ravny:
ravny:
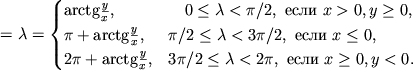 |
Vernemsya k ris. 2.5. Cherez proizvol'no vybrannye tochki ![]() i
i ![]() provedem bol'shoi krug. Polyusy oboznachim kak
provedem bol'shoi krug. Polyusy oboznachim kak ![]() i
i ![]() .
Provedem teper' cherez polyusy i tochku
.
Provedem teper' cherez polyusy i tochku ![]() bol'shoi krug (analogichno
provedem bol'shoi krug cherez tochku
bol'shoi krug (analogichno
provedem bol'shoi krug cherez tochku ![]() ). Oboznachim cherez
). Oboznachim cherez ![]() central'nyi ugol mezhdu napravleniem na tochku
central'nyi ugol mezhdu napravleniem na tochku ![]() i napravleniem na
proizvol'nuyu tochku
i napravleniem na
proizvol'nuyu tochku ![]() , lezhashuyu na sfere v ploskosti bol'shogo
kruga
, lezhashuyu na sfere v ploskosti bol'shogo
kruga ![]() . Provedem cherez tochku
. Provedem cherez tochku ![]() ploskost',
parallel'nuyu bol'shomu krugu
ploskost',
parallel'nuyu bol'shomu krugu ![]() . Poluchennaya ploskost' yavlyaetsya
malym krugom, i radius
. Poluchennaya ploskost' yavlyaetsya
malym krugom, i radius ![]() okruzhnosti raven, esli
okruzhnosti raven, esli
![]() :
:
Vvedem dekartovu sistemu koordinat: os' ![]() napravim vdol' radiusa
napravim vdol' radiusa
![]() , os'
, os' ![]() -- vdol' radiusa
-- vdol' radiusa ![]() . Oboznachim edinichnye vektory
osei
. Oboznachim edinichnye vektory
osei ![]() i
i ![]() kak
kak ![]() i
i ![]() , sootvetstvenno. Napravlenie
osi
, sootvetstvenno. Napravlenie
osi ![]() zadadim edinichnym vektorom
zadadim edinichnym vektorom ![]() soglasno uravneniyu:
soglasno uravneniyu:
Vektornoe proizvedenie (2.22) vektorov
Oboznachim cherez ![]() dvugrannyi ugol mezhdu ploskostyami
dvugrannyi ugol mezhdu ploskostyami
![]() i
i ![]() . Chisla
. Chisla
![]() nazyvayutsya
sfericheskimi koordinatami tochki
nazyvayutsya
sfericheskimi koordinatami tochki ![]() . Pri
. Pri ![]() dostatochno
znat' dve koordinaty
dostatochno
znat' dve koordinaty
![]() dlya opredeleniya polozheniya
tochki na sfere. V sleduyushei glave budut opredeleny razlichnye
sistemy sfericheskih koordinat. V kazhdoi iz nih koordinaty
dlya opredeleniya polozheniya
tochki na sfere. V sleduyushei glave budut opredeleny razlichnye
sistemy sfericheskih koordinat. V kazhdoi iz nih koordinaty
![]() imeyut raznye nazvaniya i mogut oboznachat'sya drugimi
bukvami.
imeyut raznye nazvaniya i mogut oboznachat'sya drugimi
bukvami.
Pust' tochka ![]() lezhit na sfere i yavlyaetsya tochkoi peresecheniya
bol'shogo kruga
lezhit na sfere i yavlyaetsya tochkoi peresecheniya
bol'shogo kruga ![]() i malogo kruga
i malogo kruga ![]() (ris. 2.5). Naidem dlinu dugi
(ris. 2.5). Naidem dlinu dugi
![]() . Tak kak
central'nyi ugol
. Tak kak
central'nyi ugol ![]() raven
raven ![]() , to
, to
Rassmotrim bolee podrobno vopros preobrazovaniya koordinat vektora v krivolineinyh koordinatah.
V krivolineinoi sisteme koordinat v otlichie ot dekartovoi
vozmozhny dva sposoba vybora bazisnoi troiki vektorov: 1) bazisnye
vektory yavlyayutsya kasatel'nymi v tochke
![]() k krivym
k krivym
![]() ,
,
![]() ,
,
![]() ; oboznachim ih kak
; oboznachim ih kak
![]() ,
,
![]() ,
,
![]() i 2) bazisnye vektory
perpendikulyarny v tochke
i 2) bazisnye vektory
perpendikulyarny v tochke
![]() k poverhnostyam,
zadavaemym funkciyami
k poverhnostyam,
zadavaemym funkciyami
![]() , t.e.
, t.e.
![]() ,
,
![]() ,
,
![]() ; oboznachim ih kak
; oboznachim ih kak
![]() ,
,
![]() ,
,
![]() . Eshe odnim otlichiem ot
dekartovoi sistemy yavlyaetsya to, chto napravlenie, a takzhe dlina
bazisnyh vektorov mozhet razlichat'sya v raznyh tochkah prostranstva.
. Eshe odnim otlichiem ot
dekartovoi sistemy yavlyaetsya to, chto napravlenie, a takzhe dlina
bazisnyh vektorov mozhet razlichat'sya v raznyh tochkah prostranstva.
V sluchae sfericheskih koordinat poverhnost', zadavaemaya uravneniem
![]() , est' sfera radiusa
, est' sfera radiusa ![]() , uravnenie
, uravnenie
![]() opredelyaet malyi krug, a
opredelyaet malyi krug, a
![]() -- ploskost' meridiana. Peresecheniya
etih ploskostei so sferoi yavlyayutsya okruzhnostyami. Tak kak krivye
-- ploskost' meridiana. Peresecheniya
etih ploskostei so sferoi yavlyayutsya okruzhnostyami. Tak kak krivye
![]() ,
,
![]() ,
,
![]() takzhe yavlyayutsya
okruzhnostyami, to v sluchae sfericheskih koordinat obe bazisnye
troiki sovpadayut. V obshem sluchae eto ne tak.
takzhe yavlyayutsya
okruzhnostyami, to v sluchae sfericheskih koordinat obe bazisnye
troiki sovpadayut. V obshem sluchae eto ne tak.
Dva vybora bazisnyh troek dayut vozmozhnost' naiti proekcii vektora
![]() kak na osi
kak na osi
![]() ,
,
![]() ,
,
![]() ,
tak i na osi
,
tak i na osi
![]() ,
,
![]() ,
,
![]() :
:
indeksy summirovaniya mogut oboznachat'sya lyubymi bukvami.
Chisla
![]() nazyvayutsya
kontravariantnymi, a
nazyvayutsya
kontravariantnymi, a
![]() --
kovariantnymi proekciyami
vektora
--
kovariantnymi proekciyami
vektora
![]() .
.
Dlya bazisnyh vektorov
![]() spravedlivy
sootnosheniya:
spravedlivy
sootnosheniya:
Simvol
Skalyarnoe proizvedenie v krivolineinyh koordinatah zapisyvaetsya v vide
Dlya togo, chtoby poluchit' yavnoe vyrazhenie kovariantnyh i
kontravariantnyh koordinat vektora, umnozhim skalyarno pervoe iz
uravnenii (2.24) na
![]() , a vtoroe -- na
, a vtoroe -- na
![]() . Uchityvaya opredelenie (2.25), naidem:
. Uchityvaya opredelenie (2.25), naidem:
Znachit,
Ispol'zuya formuly (2.26), perepishem (2.24) v vide:
Sootnosheniya spravedlivy dlya lyubogo vektora
![]() . Esli vmesto
. Esli vmesto
![]() v (2.27) podstavit' bazisnye vektory, to poluchim:
v (2.27) podstavit' bazisnye vektory, to poluchim:
Vvodya oboznacheniya
perepishem sootnosheniya (2.28) takim obrazom:
Dlya postroeniya bazisnoi troiki
![]() po vektoram
po vektoram
![]() neobhodimo znat' matricu s elementami
neobhodimo znat' matricu s elementami ![]() ; i,
naoborot, dlya postroeniya bazisa
; i,
naoborot, dlya postroeniya bazisa
![]() po bazisu
po bazisu
![]() -- matricu s elementami
-- matricu s elementami ![]() . Eti matricy
vzaimno obratny, t.e.
. Eti matricy
vzaimno obratny, t.e.
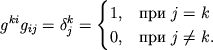
Velichiny ![]() i
i ![]() nazyvayutsya komponentami dvazhdy
kontravariantnogo i kovariantnogo metricheskogo
tenzora, sootvetstvenno.
nazyvayutsya komponentami dvazhdy
kontravariantnogo i kovariantnogo metricheskogo
tenzora, sootvetstvenno.
Chto iz sebya predstavlyaet tenzor v matematike? Kak my videli, zadanie bazisnoi troiki opredelyaet sistemu koordinat, v kotoroi mozhno naiti koordinaty proizvol'nyh vektorov, t.e. ih proekcii na bazisnye vektory. No tak kak pri perehode v druguyu tochku prostranstva napravlenie i velichina bazisnyh vektorov mozhet menyat'sya, to neobhodimo reshit' zadachu o preobrazovanii proekcii proizvol'nyh vektorov iz odnoi bazisnoi troiki v druguyu. Eta zadacha reshaetsya metodami tenzornogo analiza. Tenzory predstavlyayut soboi sistemu velichin, preobrazuyushihsya po lineinomu zakonu pri perehode ot odnoi sistemy koordinat k drugoi. Sootnosheniya, zapisannye v tenzornoi forme, sohranyayut svoyu formu v lyuboi koordinatnoi sisteme.
Naidem teper' rasstoyanie
![]() mezhdu dvumya beskonechno
blizkimi tochkami prostranstva. Dekartovy koordinaty vektora
mezhdu dvumya beskonechno
blizkimi tochkami prostranstva. Dekartovy koordinaty vektora
![]() ravny
ravny ![]() . Dlya etogo, schitaya
. Dlya etogo, schitaya ![]() v
formulah (2.20) funkciyami peremennyh
v
formulah (2.20) funkciyami peremennyh
![]() naidem
differencialy
naidem
differencialy ![]() ,
, ![]() ,
, ![]() . Po pravilu vychisleniya
differencialov funkcii mnogih peremennyh, snachala fiksiruem
peremennye
. Po pravilu vychisleniya
differencialov funkcii mnogih peremennyh, snachala fiksiruem
peremennye
![]() i nahodim izmenenie funkcii (chastnuyu
proizvodnuyu
i nahodim izmenenie funkcii (chastnuyu
proizvodnuyu
![]() ) v zavisimosti ot prirasheniya
) v zavisimosti ot prirasheniya ![]() ,
zatem fiksiruem peremennye
,
zatem fiksiruem peremennye ![]() i
i ![]() i nahodim izmenenie
funkcii v zavisimosti ot prirasheniya
i nahodim izmenenie
funkcii v zavisimosti ot prirasheniya ![]() , i nakonec pri
postoyannyh
, i nakonec pri
postoyannyh ![]() i
i ![]() nahodim chastnuyu proizvodnuyu
nahodim chastnuyu proizvodnuyu
![]() . V rezul'tate poluchim:
. V rezul'tate poluchim:
Po opredeleniyu chastnye proizvodnye
![]() i dr. yavlyayutsya kasatel'nymi k
funkciyam
i dr. yavlyayutsya kasatel'nymi k
funkciyam ![]() , t.e. predstavlyayut soboi komponenty bazisnyh
vektorov
, t.e. predstavlyayut soboi komponenty bazisnyh
vektorov
![]() ,
,
![]() ,
,
![]() vdol'
napravlenii
vdol'
napravlenii
![]() :
:
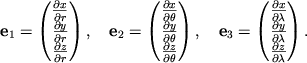
Sledovatel'no, differencial funkcii yavlyaetsya kontravariantnym
vektorom. Pereoboznachiv beskonechno malye prirasheniya kak
![]() ,
, ![]() ,
, ![]() , naidem kvadrat rasstoyaniya
, naidem kvadrat rasstoyaniya ![]() mezhdu dvumya beskonechno blizkimi tochkami, kotoryi ravnyaetsya v
dekartovoi sisteme koordinat
mezhdu dvumya beskonechno blizkimi tochkami, kotoryi ravnyaetsya v
dekartovoi sisteme koordinat
V bolee obshem vide s uchetom pravila summirovaniya vyrazhenie dlya kvadrata rasstoyaniya mezhdu dvumya tochkami prostranstva zapisyvaetsya v vide:
gde
Vybor toi ili inoi sistemy koordinat daet vozmozhnost' opredelit' polozhenie tela v prostranstve i uprostit' uravneniya dvizheniya tela, no ne opredelyaet svoistva samogo prostranstva. Zadanie metriki sovmestno s opredeleniem sistemy koordinat polnost'yu opisyvaet prostranstvo. Eto oznachaet, chto, znaya metricheskii tenzor, mozhno vychislit' rasstoyanie mezhdu dvumya tochkami. V sluchae evklidova prostranstva, kotoroe nazyvaetsya ploskim, rasstoyanie nahoditsya po formule (2.32) i metricheskii tenzor raven
V sluchae ploskogo prostranstva metricheskii tenzor
Esli prostranstvo ne yavlyaetsya ploskim, to dlya vychisleniya rasstoyanii uzhe nel'zya ispol'zovat' zakon Pifagora (2.32). V chastnosti, pri vychisleniyah na sfere (v krivom prostranstve) dlina dugi mezhdu dvumya tochkami ne ravna dline hordy (rasstoyaniyu v ploskom prostranstve).
Kvadrat elementa dliny v sfericheskoi sisteme koordinat legko
naiti, vychisliv chastnye proizvodnye
![]() i t.d. i podstaviv ih
v (2.32). Ispol'zuya uravneniya (2.20), nahodim, chto
i t.d. i podstaviv ih
v (2.32). Ispol'zuya uravneniya (2.20), nahodim, chto
![]() ,
,
![]() i t.d. V rezul'tate
posle privedeniya podobnyh chlenov poluchim, chto
i t.d. V rezul'tate
posle privedeniya podobnyh chlenov poluchim, chto
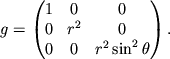
Takim obrazom, svoistva geometrii v krivolineinoi sisteme
koordinat opredelyayutsya komponentami ![]() metricheskogo
tenzora. V dal'neishem my budem rassmatrivat' chetyrehmernoe
prostranstvo-vremya dlya vychisleniya effektov teorii otnositel'nosti
(izmeneniya hoda chasov, nahodyashihsya v gravitacionnom pole,
otkloneniya lucha sveta). V chetyrehmernom prostranstve-vremeni
imeetsya, sledovatel'no, 16 komponent tenzora, iz nih tol'ko 10
razlichny iz-za simmetrichnosti tenzora (chetyre s odinakovymi
indeksami i
metricheskogo
tenzora. V dal'neishem my budem rassmatrivat' chetyrehmernoe
prostranstvo-vremya dlya vychisleniya effektov teorii otnositel'nosti
(izmeneniya hoda chasov, nahodyashihsya v gravitacionnom pole,
otkloneniya lucha sveta). V chetyrehmernom prostranstve-vremeni
imeetsya, sledovatel'no, 16 komponent tenzora, iz nih tol'ko 10
razlichny iz-za simmetrichnosti tenzora (chetyre s odinakovymi
indeksami i ![]() s razlichnymi indeksami).
s razlichnymi indeksami).
<< 2.2. Skalyary, vektory, tenzory | Oglavlenie | 2.4. Osnovnye formuly sfericheskoi >>
|
Publikacii s klyuchevymi slovami:
astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni
Publikacii so slovami: astrometriya - sfericheskaya astronomiya - sistemy koordinat - shkaly vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |