Astronet > Protozvezdy. Gde, kak i iz chego formiruyutsya zvezdy

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 4. Ot N'yutona do Dzhinsa | Oglavlenie | 6. Kakie zvezdy rozhdayutsya >>

Ot Dzhinsa do nashih dnei

"...razumno nadeyat'sya, chto v ne slishkom otdalennom budushem my smozhem ponyat' takuyu prostuyu vesh', kak zvezda." [24]

A. Eddington, 1926 g.

"...chem bol'she my poznaem deistvitel'noe sostoyanie takogo slozhnogo fizicheskogo obrazovaniya, kakim yavlyaetsya zvezda, tem bolee zaputannym ono nam predstavlyaetsya." [32]

M. Shvarcshil'd, 1960 g.

Dzheims Hopvud Dzhins (ris. 5.1), tol'ko chto blestyashe zakonchivshii Kembridzhskii universitet, v techenie neskol'kih let vypolnyaet seriyu vydayushihsya rabot po raznym razdelam teoreticheskoi fiziki: on publikuet monografiyu po kineticheskoi teorii gazov, issledovaniya po molekulyarnoi fizike i teorii izlucheniya [33]. V nachale 1900-h godov pod vliyaniem professora astronomii i fiziki Kembridzhskogo universiteta Dzhordzha Govarda Darvina (syna znamenitogo biologa Charlza Darvina) Dzheims Dzhins vypolnyaet seriyu rabot po teoreticheskoi astrofizike. Sredi nih byla i fundamental'naya rabota "Ustoichivost' sfericheskoi tumannosti", opublikovannaya v 1902 g. v "Soobsheniyah Londonskogo korolevskogo obshestva". Dzheimsu v tu poru bylo 25 let. Eta rabota o povedenii gazovyh uplotnenii pod deistviem sily samogravitacii stala fundamentom sovremennoi teorii gravitacionnoi neustoichivosti, ob'yasnyayushei proishozhdenie prakticheski vseh strukturnyh elementov Vselennoi - ot galaktik i ih skoplenii, do zvezd, planet i ih sputnikov. Harakternye razmer i massa gravitacionno-neustoichivyh gazovyh uplotnenii nazyvayutsya s teh por dzhinsovskimi i otmechayutsya indeksom J (ot James Jeans), naprimer, M_J - dzhinsovskaya massa, R_J - dzhinsovskii .radius.

Voobshe, Dzh. Darvin mog gordit'sya tem, chto privlek vnimanie molodogo Dzhinsa k astronomii: ego podopechnyi sdelal ochen' mnogoe dlya razvitiya kosmogonii i zvezdnoi dinamiki.

Dzheims Hopvud Dzhins

Ris. 5.1. Dzheims Hopvud Dzhins - sozdatel' teorii gravitacionnoi neustoichivosti. Etot portret nahoditsya v galeree Londonskogo korolevskogo obshestva, chlenom, a zatem i sekretarem kotorogo dolgie gody byl vydayushiisya uchenyi

No mog li predpolagat' Dzh. Darvin, zanimavshii v 1899-1900 gg. post prezidenta Korolevskogo astronomicheskogo obshestva, chto cherez chetvert' veka na etu pochetnuyu dolzhnost' vstupit Dzh. Dzhinc i v pamyat' o svoem nastavnike uchredit ezhegodnye Darvinovskie lekcii. Vprochem, svyaz' mezhdu Darvinym i Dzhinsom okazalas' eshe bolee glubokoi. Darvin proslavilsya izucheniem prilivov i figur vrashayushihsya zhidkih tel [29]. Dzhins prodolzhil issledovaniya kosmogonicheskoi roli prilivnyh yavlenii i dazhe razrabotal prilivnuyu teoriyu proishozhdeniya Solnechnoi sistemy, ochen' modnuyu v pervoi polovine XX veka. V etoi teorii rozhdenie planetnoi sistemy rassmatrivaetsya kak redchaishii fakt, vyzvannyi blizkim proletom ryadom s Solncem drugoi zvezdy, vyrvavshei iz obolochki Solnca sgustok proto-planetnogo veshestva [34]. I hotya v otnoshenii Solnechnoi sistemy etu gipotezu vspominayut seichas lish' kak istoricheskii fakt, sam mehanizm prilivnogo vzaimodeistviya nesomnenno igraet bol'shuyu rol' v mire galaktik, zvezdnyh skoplenii i, vozmozhno, protozvezd [35].

Vernemsya, odnako, k teorii gravitacionnoi neustoichivosti. Posle togo, kak v nachale XX veka Dzh. Dzhins zalozhil ee fundament, astronomam ponadobilos' eshe 70 let dlya obnaruzheniya imenno togo komponenta mezhzvezdnoi sredy, kotoryi neposredstvenno svyazan s formirovaniem zvezd i pri opisanii kotorogo teoriya Dzhinsa pravil'no predskazyvaet massy i razmer novorozhdennyh zvezd. Davaite kratko poznakomimsya s etoi teoriei.

N'yuton, razvivaya ideyu gravitacionnoi kondensacii pervichnogo veshestva, predpolagal eto veshestvo sovershenno inertnym, holodnym, ne soprotivlyayushimsya gravitacii. Poetomu on schital, chto lyubaya neodnorodnost' plotnosti dolzhna progressivno szhimat'sya i uplotnyat'sya siloi tyazhesti. K koncu XIX veka fiziki uzhe yasno ponimali, chto vsyakoe veshestvo, v tom chisle i razrezhennyi gaz, obladaet uprugost'yu: imenno eto svoistvo gaza pozvolyaet rasprostranyat'sya v nem zvukovym volnam. Poetomu Dzhins zaklyuchil, chto process gravitacionnogo szhatiya mozhet nachat'sya lish' v tom sluchae, esli sila tyazhesti pobedit silu gazovogo davleniya.

Obychno, chtoby opisat' rasprostranenie zvuka v gaze, fiziki zapisyvayut uravnenie kolebanii, v kotoroe vhodyat inercionnye harakteristiki gaza (plotnost', massa molekul) i silovye (davlenie). Dzhine vpervye dobavil v eto uravnenie novyi chlen, uchityvayushii gravitacionnoe vzaimodeistvie chastic gaza. Okazalos', chto pri etom uravnenie poluchilo novye resheniya; pri vysokoi chastote kolebanii, t. e. pri maloi dline volny, ego resheniem po-prezhnemu ostavalis' begushie ili stoyachie zvukovye volny, no chem bol'she stanovitsya dlina volny, tem sil'nee chuvstvuetsya vliyanie gravitacii, i, nakonec, pri opredelennoi kriticheskoi dline volny l_J rasprostranenie zvukovyh voln prekrashaetsya. Vse uplotneniya v gaze, harakternyi razmer kotoryh prevyshaet l_J, dolzhny neuderzhimo szhimat'sya pod deistviem sobstvennoi sily tyazhesti - gazovoe davlenie ne mozhet protivostoyat' etomu.

Ob'yasnit' eto yavlenie mozhno dovol'no prosto. Rassmotrim, kakie processy proishodyat pri nebol'shom sluchainom szhatii oblaka gaza s harakternym razmerom l i plotnost'yu r. S odnoi storony, sila gravitacii stremitsya prodolzhit' eto szhatie. Esli by gazovoe davlenie voobshe otsutstvovalo, to vse veshestvo upalo by k centru oblaka za vremya svobodnogo padeniya (free fall time):

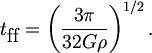
$\large$$t_{\textrm{ff}}=\left(\frac{3\pi}{32G\rho}\right)^{1/2}.$$$ (5.1)

Eto vyrazhenie legko mozhno poluchit' iz Tret'ego zakona Keplera: vremya poluoborota po ochen' vytyanutoi ellipticheskoi orbite, t. e. vremya svobodnogo padeniya, ravno p(l³/GM)^1/2, a massa oblaka M = 4pl³r/3.

S drugoi storony, v sluchae otsutstviya gravitacii sily gazovogo davleniya zastavili by oblako rasshirit'sya za dinamicheskoe (dynamic), vremya: t_dyn = l/V_s, gde V_s - skorost' zvuka, kotoraya zavisit tol'ko ot temperatury i himicheskogo sostava gaza. Esli vozmusheniya plotnosti v gaze slaby (t. e. r » r₀ i T » T₀), to otnoshenie t_dyn / t_ff ~ l. Znachit, v vozmusheniyah plotnosti malen'kogo razmera (t_dyn << t_ff) gazovoe davlenie vsegda budet uspevat' pereraspredelit' veshestvo takim obrazom, chtoby vosprepyatstvovat' dal'neishemu szhatiyu. I naprotiv, vozmusheniya plotnosti bol'shogo razmera (t_dyn >> t_ff), sluchaino vozniknuv, uzhe ne smogut vnov' rasshirit'sya: u nih dlya etogo prosto ne hvatit vremeni, tak kak gravitaciya srabotaet bystree, chem sila gazovogo davleniya.

Kakovy zhe kriticheskie znacheniya l_J i M_J? Grubo ih mozhno ocenit', priravnyav drug drugu t_ff i t_dyn, a bolee tochno - iz usloviya ravnovesiya gaza pod deistviem davleniya i sily tyazhesti. Zvukovaya volna - eto ciklicheskii process szhatiya i razrezheniya gaza: polperioda dlitsya szhatie, polperioda - razrezhenie. Znachit, harakternyi razmer oblasti uplotneniya l/2, a ee massa M = r(l/2)³. Izvestno, chto davlenie ideal'nogo gaza R = RTr/m, gde R = 8,31 10³ Dzh/K kg - universal'naya gazovaya postoyannaya, a T i m - temperatura i molekulyarnyi ves gaza. Ochevidno, vytalkivayushaya sila, deistvuyushaya na edinichnyi ob'em gaza, v pervom priblizhenii ravna P/(l/4), a sila tyagoteniya, stremyashayasya pogruzit' element ob'ema gaza vnutr' vozmusheniya plotnosti, mozhet byt' zapisana tak: GMr/(l/4)². Dlina volny i massa vozmusheniya stanovyatsya kriticheskimi, kogda eti sily ravny: 4P/l_J = GM_Jr/(l_J/4)². Otsyuda:

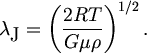
$\large$$\lambda_{\textrm{J}}=\left(\frac{2RT}{G\mu\rho}\right)^{1/2}.$$$ (5.2)

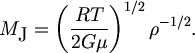
$\large$$M_{\textrm{J}}=\left(\frac{RT}{2G\mu}\right)^{1/2}\rho^{-1/2}.$$$ (5.3)

Poslednyaya formula yavlyaetsya vazhneishei v teorii gravitacionnoi neustoichivosti Dzhinsa. Iz nee sleduet, chto esli v pokoyasheisya razrezhennoi srede v silu kakih-to prichin voznikayut vozmusheniya plotnosti razlichnogo masshtaba, to te iz nih, massa kotoryh M > M_J, dolzhny neuderzhimo szhimat'sya i uplotnyat'sya. Obychno v gaze vozmusheniya plotnosti malyh masshtabov preobladayut nad krupnomasshtabnymi, poetomu naibolee veroyatno, chto gravitacionnoi neustoichivosti podvergnutsya vozmusheniya s massoi M » M_J.

Spustya 240 let posle pis'ma N'yutona k Bentli Dzhine napisal v svoei knige "Zvezdy v ih razvitii" (v russkom perevode - "Dvizhenie mirov" [36]): "Predpolozhim, chto v nachale vremen vse prostranstvo bylo zapolneno gazom... Togda mozhno dokazat', chto gaz ne ostavalsya by ravnomerno raspredelennym v prostranstve, a nemedlenno stal by sobirat'sya v shary. My mozhem vychislit', skol'ko gaza potrebuetsya dlya obrazovaniya kazhdogo shara". K sozhaleniyu, Dzhins nemnogo preuvelichival svoi vozmozhnosti: on ne mog dostatochno ubeditel'no proverit' rabotosposobnost' svoih formul, tak kak v to vremya pochti nichego ne bylo izvestno o fizicheskih svoistvah i sostave mezhzvezdnogo gaza, iz kotorogo formiruyutsya zvezdy. Odnako teper' my mozhem eto sdelat'.

Himicheskii sostav zvezd i mezhzvezdnogo gaza otlichaetsya bol'shoi stabil'nost'yu: na 1000 atomov vodoroda prihoditsya okolo 100 atomov geliya i 2-3 atoma bolee tyazhelyh elementov. V plotnyh holodnyh oblakah, v kotoryh formiruyutsya zvezdy, vodorod nahoditsya v forme molekul N₂, molekulyarnyi ves kotoryh m(N₂) = 2. S uchetom vseh drugih himicheskih elementov srednii molekulyarnyi ves gaza v oblakah sostavlyaet m = 2.3. Ispol'zuya eto znachenie, udobno normirovat' formulu (5.3) na harakternye parametry mezhzvezdnogo gaza:

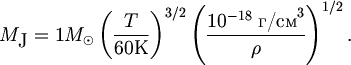
$\large$$M_{\textrm{J}}=1M_\odot \left(\frac{T}{60\textrm{K}}\right)^{3/2} \left(\frac{10^{-18}~\mbox{\rm g/sm}^3}{\rho}\right)^{1/2}.$$$ (5.4)

Kak my uvidim dalee, tipichnymi mestami formirovaniya zvezd yavlyayutsya melkomasshtabnye kondensacii v molekulyarnyh oblakah, gde temperatura T = (5 - 20) K i plotnost' T = (10^-20 - 10^-18) g/sm³. Podstaviv eti znacheniya v formulu Dzhinsa, my opredelim, chto M_J = (0.02 - 2) M. Deistvitel'no, massy bol'shinstva zvezd zaklyucheny imenno v etom diapazone - ubeditel'nyi argument v pol'zu teorii gravitacionnoi neustoichivosti. Eshe odnim testom dlya etoi teorii mozhet sluzhit' razmer oblaka - predka zvezdy. Dlya Solnechnoi sistemy etot razmer iz nablyudenii ocenivaetsya v 10⁴ a. e.: imenno v etom ob'eme sosredotochena osnovnaya massa yader komet (tak nazyvaemoe, vnutrennee oblako Oorta). A chto predskazyvaet na etot schet teoriya Dzhinsa?

Radiusom gazovogo fragmenta v moment nastupleniya ego gravitacionnoi neustoichivosti estestvenno schitat' velichinu R_J = l_J/4, znachenie kotoroi

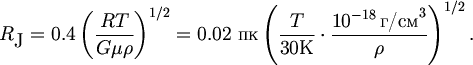
$\large$$R_{\textrm{J}}=0.4\left(\frac{RT}{G\mu\rho}\right)^{1/2} =0.02\mbox{\rm~pk}\left(\frac{T}{30\textrm{K}}\cdot \frac{10^{-18}\,\mbox{\rm g/sm}^3}{\rho}\right)^{1/2}.$$$ (5.5)

V poslednie gody, govorya o plotnosti mezhzvezdnoi sredy, astronomy vse chashe ispol'zuyut ne massovuyu plotnost' r, a koncentraciyu molekul vodoroda n(H₂). Poetomu formuly (5.4) i (5.5) mozhno perepisat' v bolee udobnoi forme, ispol'zuya ochevidnoe sootnoshenie

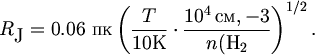
$\large$$R_{\textrm{J}}=0.06\mbox{\rm~pk} \left(\frac{T}{10\textrm{K}}\cdot \frac{10^4\,\mbox{\rm sm},{-3}}{n(\mathrm{H}_2}\right)^{1/2}.$$$ (5.6)

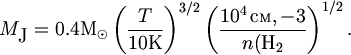
$\large$$M_{\textrm{J}}=0.4\textrm{M}_\odot \left(\frac{T}{10\textrm{K}}\right)^{3/2} \left(\frac{10^4\,\mbox{\rm sm},{-3}}{n(\mathrm{H}_2}\right)^{1/2}.$$$ (5.7)

Dlya tipichnyh parametrov gaza v oblastyah zvezdoobrazovaniya - T = 20 K i n(H₂) = 10⁴ sm^-3, - privodyashih k znacheniyu M_J = 1.4 M, teoriya predskazyvaet kriticheskii radius oblaka R_J = 0.08 pk » 10⁴ a. e. Takoe horoshee sovpadenie znacheniya R_J i nablyudaemogo razmera Solnechnoi sistemy takzhe yavlyaetsya vpechatlyayushim svidetel'stvom v pol'zu teorii Dzhinsa.

Razumeetsya, prostye formuly Dzhinsa ne uchityvayut mnogih fizicheskih processov, proishodyashih v mezhzvezdnoi srede. Eti formuly verny dlya ideal'nogo pokoyashegosya odnorodnogo gaza, kotoryi v prirode nikogda ne vstretish'. Mezhzvezdnoe veshestvo nahoditsya v postoyannom dvizhenii so skorost'yu, chasto prevoshodyashei skorost' zvuka; ono ispytyvaet sil'noe vliyanie magnitnogo polya, prityazhenie k zvezdam Galaktiki i luchevoe davlenie so storony naibolee yarkih iz nih. Poetomu mnogie fiziki posle Dzhinsa bralis' za utochnenie i razvitie teorii gravitacionnoi neustoichivosti. Otmetim sredi nih E.M. Lifshica, S. Chandrasekara, Ya.B. Zel'dovicha, Dzh. Silka. Seichas eta teoriya razvita vpolne detal'no: ona uchityvaet rasshirenie i vrashenie gazovoi sredy, ee vzaimodeistvie s magnitnym polem i s drugimi istochnikami gravitacii. Tem, kto zahochet poznakomit'sya s ee matematicheskim apparatom i osnovnymi prilozheniyami, sovetuem vospol'zovat'sya knigami [37-40].

Vazhno, odnako, chto uchet dopolnitel'nyh fizicheskih faktorov principial'no ne izmenil vyvody teorii: znacheniya dzhinsovskoi massy i dzhinsovskogo radiusa, opredelennye formulami (5.6) i (5.7), do sih por ispol'zuyutsya v bol'shinstve rabot pri ocenke rezul'tatov gravitacionnoi neustoichivosti. Otchasti eto svyazano s tem, chto iz nablyudenii redko udaetsya poluchit' inye harakteristiki protozvezdnoi sredy, krome ee plotnosti i temperatury.

Sam Dzhins byl chrezvychaino voodushevlen rezul'tatom svoih issledovanii i prezhde vsego ih naglyadnost'yu i prostotoi. On pisal: "...dlya nas yasno, pochemu vse zvezdy imeyut ochen' shodnyi ves; eto potomu, chto vse oni obrazovany odinakovym processom. Oni, pozhalui, pohozhi na fabrichnye izdeliya, sdelannye odnoyu i toyu zhe mashinoi" [36]. Znaya segodnya, chto zvezdy razlichayutsya po masse v tysyachi raz, a usloviya v mezhzvezdnoi srede - eshe sil'nee, my vprave nazvat' optimizm Dzhinsa prezhdevremennym. Odnako on i sam ponimal, chto proiden lish' pervyi rubezh, i, predvidya gryadushie trudnosti, s kotorymi stolknetsya teoriya formirovaniya zvezd i galaktik, zaklyuchil: "Pri sovremennom sostoyanii vashih znanii lyubaya popytka diktovat' okonchatel'nye resheniya po osnovnym problemam kosmogonii byla by nichem inym, kak chistym dogmatizmom".

<< 4. Ot N'yutona do Dzhinsa | Oglavlenie | 6. Kakie zvezdy rozhdayutsya >>

Publikacii s klyuchevymi slovami: Protozvezdy - zvezdoobrazovanie Publikacii so slovami: Protozvezdy - zvezdoobrazovanie
Sm. takzhe: IC 348 i Barnard 3 M16: stolpy sozidaniya Vybrosy iz protozvezd v Zmee CG4: globula i galaktika NGC 604: gigantskie zvezdnye yasli NGC 7714: vspyshka zvezdoobrazovaniya posle stolknoveniya galaktik Tumannost' Konus ot teleskopa imeni Habbla Vse publikacii na tu zhe temu >>

Mneniya chitatelei [4]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce