Astronet > 1. Matematicheskii apparat klassifikacii

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< Vvedenie | Oglavlenie | 2. Biblioteka template-spektrov >>

Razdely

1.1. Pervyi uroven' obrabotki fotometricheskih dannyh - sposoby predstavleniya dannyh
1.2. Vtoroi uroven' obrabotki fotometricheskih dannyh - matematicheskii i statisticheskii apparat
1.3. Tretii uroven' obrabotki fotometricheskih dannyh - ispol'zovanie dopolnitel'nyh svedenii

1. Matematicheskii apparat klassifikacii

Matematicheskii i statisticheskii podhod k klassifikacii ob'ektov po fotometricheskim dannym mozhno razdelit' na tri urovnya. Pod pervym urovnem budem ponimat' sposob ispol'zovaniya fotometricheskih dannyh, pod vtorym - algoritm, primenyaemyi dlya raboty s dannymi, a pod tret'im - dopolnitel'nuyu korrekciyu rezul'tatov, provodimuyu za schet privlecheniya dopolnitel'nyh svedenii. Vybor vernogo puti po etim urovnyam v znachitel'noi mere opredelyaet uspeh klassifikacii.

1.1. Pervyi uroven' obrabotki fotometricheskih dannyh - sposoby predstavleniya dannyh

Dannye, poluchaemye v rezul'tate obrabotki nablyudenii, predstavlyayut iz sebya potoki izlucheniya ot ob'ektov v kazhdom fil'tre. Sushestvuet neskol'ko variantov predstavleniya etih dannyh dlya dal'neishei obrabotki.

Pervyi variant - vychislenie pokazatelei cveta ob'ektov, to est' raznostei zvezdnyh velichin, poluchaemyh iz potokov v kazhdom fil'tre. Obsheprinyatym v nastoyashee vremya yavlyaetsya ispol'zovanie tak nazyvaemyh AB-velichin, predlozhennyh Oke [19]. V etom sluchae primenyayutsya $F_{\nu}$ -potoki. Zvezdnaya velichina v fil'tre vychislyaetsya po formule:

$\begin{displaymath} AB=-2.5 \lg{\frac{\int F_{\nu}(\nu)D(\nu)d\nu}{\int D(\nu)d\nu}}-48.61 \end{displaymath}$ (1.1)

gde $F_{\nu}$ vyrazheno v $erg \cdot cm^{-2} s^{-1} Hz^{-1}$ , a $D(\nu)$ - krivaya propuskaniya fil'tra.
Gruppa nemeckih issledovatelei iz instituta im.Maksa Planka (obzor CADIS), kotoraya rabotaet s pokazatelyam cvetov ob'ektov, ispol'zuet zvezdnye velichiny, poluchaemye iz potokov ot ob'ektov, vyrazhennyh v $\gamma \cdot m^{-2} s^{-1}$ $^{-1}$ , kak prinyato v rentgenovskoi astronomii.
Dalee mozhno stroit' dvucvetnye diagrammy dlya razlichnyh kombinacii pokazatelei cveta i pytat'sya razdelyat' razlichnye tipy ob'ektov po oblastyam lokalizacii na etih diagrammah. Takie raboty provodyatsya s nachala 60-h godov. Seichas etot podhod razvivaet vysheupomyanutaya gruppa nemeckih issledovatelei. On zhe ispol'zuetsya pri vybore ob'ektov dlya spektroskopii v obzore SDSS. Kak pokazano v rabotah [6,7], pri pomoshi analiza znachenii pokazatelei cveta v situacii s bol'shim chislom fil'trov, stanovitsya vozmozhnym dovol'no tochnoe opredelenie krasnogo smesheniya dlya vnegalakticheskih ob'ektov (oshibka v opredelenii 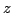men'she 0.1).
V nastoyashee vremya v svyazi s moshnym i bystrym razvitiem vychislitel'nyh sredstv stanovitsya vozmozhnym stroit' klassifikaciyu ob'ektov v mnogomernom prostranstve cvetov pri pomoshi metodov klasternogo analiza, kogda kazhdomu tipu ob'ektov sootvetstvuyut svoi oblasti svyaznosti.
Ser'eznym nedostatkom podhoda, ispol'zuyushego pokazateli cveta, mozhno schitat' uvelichenie oshibok pri ih nahozhdenii za schet togo, chto obe zvezdnye velichiny, ispol'zuemye v raschetah, izvestny s oshibkami, sootvetstvenno vzyatie ih raznosti uvelichivaet absolyutnuyu i otnositel'nuyu oshibki znacheniya pokazatelya cveta.
Vtoroi variant, kotoryi v nastoyashee vremya aktivno ispol'zuetsya znachitel'noi chast'yu nauchnyh kollektivov, rabotayushih po dannoi tematike, zaklyuchaetsya v postroenii zavisimostei potoka (AB-velichiny, pokazatelya cveta) ot dliny volny ili chastoty, i dal'neishem analize etoi zavisimosti. V sluchae ispol'zovaniya potokov dannaya zavisimost' nazyvaetsya raspredeleniem energii v spektre ob'ekta (Spectral Energy Distribution, SED) i predstavlyaet soboi, po suti, nizkodispersionnyi spektr ob'ekta. Posle etogo proizvoditsya sravnenie SED klassificiruemyh ob'ektov s SED ob'ektov izvestnogo tipa i krasnogo smesheniya, libo s model'nymi dannymi. Pervym issledovatelem, primenivshih etot metod dlya poiska vnegalakticheskih ob'ektov, byl Baum v 1962 godu (sm gl. 1).
Teper' mozhno rassmotret', v kakom vide luchshe predstavlyat' dannye pri rabote s raspredeleniyami energii v spektrah:
1. Pervyi sposob - predstavlenie dannyh v vide potokov v fil'trah, to est' neposredstvennoe ispol'zovanie vyhodnyh dannyh fotometrii pryamyh izobrazhenii. V etom sluchae pri sravnenii raspredelenii energii v spektrah dlya ob'ektov raznoi yarkosti neobhodimo naiti normirovochnyi koefficient, kotoryi dostatochno prosto opredelyaetsya pri ispol'zovanii metoda minimizacii $\chi^2$ ili maksimal'nogo pravdopodobiya (sm. nizhe). Pri etom dannyi sposob naibolee udoben s tochki zreniya raschetov.
2. Vtoroi sposob - predstavlenie potokov ot ob'ektov v zvezdnyh velichinah. V etom sluchae, v svyazi s logarifmicheskim harakterom zvezdnyh velichin, koefficient normirovki prevrashaetsya v additivnuyu konstantu. V etom sluchae uproshayutsya raschety v sluchae ispol'zovaniya mnogomernogo polinomial'nogo priblizheniya model'nyh dannyh, no poyavlyayutsya problemy, svyazannye so slabymi ob'ektami, kogda potok blizok k nulyu i sootvetstvenno zvezdnaya velichina budet imet' bol'shie oshibki, libo vovse ne budet opredelena v sluchae otricatel'nogo znacheniya potoka. Vyhod iz etoi situacii zaklyuchaetsya v ispol'zovanii tak nazyvaemyh asinh-velichin [20].
3. Tretii sposob - ispol'zovanie pokazatelei cveta ot ob'ektov, v dannom sluchae - raznostei zvezdnyh velichin v sosednih fil'trah. Po suti eto chislennoe differencirovanie SED, poluchennogo vtorym sposobom. V etom sluchae zavisimosti pokazatelei cveta ot dliny volny dlya ob'ektov s razlichnoi yarkost'yu, no odinakovym vidom spektra, budut sovpadat' s tochnost'yu do oshibok opredeleniya pokazatelei cveta. Togda moshnye emissionnye/absorbcionnye detali v spektre budut privodit' k skachkam pokazatelei cveta v sosednih tochkah cherez nol'. Osnovnoi nedostatok takogo predstavleniya, uzhe otmechennyi vyshe - eto uvelichenie oshibok pri opredelenii pokazatelei cveta dlya slabyh ob'ektov.
V celom s matematicheskoi tochki zreniya vse tri sposoba byli by identichny pri vysokom otnoshenii signal/shum, no na praktike v sluchae predel'no slabyh ob'ektov (maloe otnoshenie signal/shum) luchshe ispol'zovat' pervyi sposob predstavleniya, pri srednih otnosheniyah signal/shum vozmozhno ispol'zovanie vtorogo sposoba, a pri vysokih - tret'ego. V dannoi rabote ispol'zuetsya pervyi sposob, to est' rabota s raspredeleniyami energii v spektrah vedetsya v terminah potokov (). Eto pozvolyaet rabotat' vo vsem diapazone otnoshenii signal/shum, chto neobhodimo dlya uspeshnoi klassifikacii ob'ektov v glubokih polyah.

1.2. Vtoroi uroven' obrabotki fotometricheskih dannyh - matematicheskii i statisticheskii apparat

Dannyi razdel soderzhit opisanie matematicheskih i statisticheskih algoritmov, prednaznachennyh dlya vtorogo varianta predstavleniya fotometricheskih dannyh. Vse matematicheskie vykladki dlya metodov approksimacii raspredelenii energii v spektrah budut privedeny dlya predstavleniya dannyh v vide potokov ( $F_{\lambda}$ ). Oni mogut byt' dostatochno prosto preobrazovany k vidu, ispol'zuyushemu dannye v lyuboi iz dvuh ostavshihsya form.

1.2.1. Metody minimizacii i maksimal'nogo pravdopodobiya

V kachestve vhodnyh dannyh my imeem znacheniya potokov ot ob'ekta v N fil'trah, ih oshibki, shablonnyi (template) spektr i krivye propuskaniya ispol'zuemyh svetofil'trov. Oboznachim nablyudaemye potoki kak $F_{i}$ , ih oshibki kak $\Delta F_{i}$ , krivye propuskaniya fil'trov kak $D_{i}(\lambda )$ , raspredelenie energii v template-spektre kak $S(\lambda )$ , model'nye potoki kak $T_{i}$ . Predpolagaetsya, chto nablyudaemye potoki ispravleny za spektral'nuyu chuvstvitel'nost' priemnika.

Togda

$\begin{displaymath} T_{i}=\int\limits_{0}S(\lambda )D_{i}(\lambda )d\lambda \end{displaymath}$

(1.2)

Kriterii $\chi ^{2}$ vychislyaetsya sleduyushim obrazom:

$\begin{displaymath} \chi ^{2}=\sum_{i=1}^{N}\frac{(\alpha T_{i}-F_{i})^{2}}{\Delta F_{i}^{2}} \end{displaymath}$

(1.3)

Gde normirovochnyi mnozhitel' $\alpha$ mozhno vychislit', ishodya iz soobrazhenii o minimume $\chi ^{2}$ , pri fiksirovannyh znacheniyah potokov, prodifferencirovav vyrazhenie dlya $\chi ^{2}$ po $\alpha$ i priravnyav znachenie proizvodnoi 0, otkuda poluchaem:

$\begin{displaymath} \alpha =\frac{\sum\limits_{i=1}^{N}{\frac{T_{i}F_{i}}{\Delta... ...}{% \sum\limits_{i=1}^{N}{\frac{T_{i}^{2}}{\Delta F_{i}^{2}}}} \end{displaymath}$

(1.4)

Vychisliv znachenie $\chi ^{2}$ legko vychislit' kriterii znachimosti:

$\begin{displaymath} P(\chi ^{2})=\frac{\int\limits_{\chi ^{2}}e^{-t}t^{\frac{N}{2}-1}dt}{% \int\limits_{0}e^{-t}t^{\frac{N}{2}-1}dt} \end{displaymath}$

(1.5)

V kachestve naibolee prostogo primera rassmotrim popytku proklassificirovat' ob'ekt kak zvezdu. Dlya etogo neobhodimo postroit' model'nye potoki dlya zvezd iz kakoi-libo biblioteki zvezdnyh spektrov, naprimer Pickles, vzyatyh v opredelennoi posledovatel'nosti, skazhem po spektral'nym klassam. Togda posle vychisleniya znacheniya $\chi^2$ dlya kazhdogo tipa spektra budet poluchena zavisimost' kriteriya znachimosti kazhdogo takogo opredeleniya ot spektral'nogo klassa i klassa svetimosti, chto pozvolit sdelat' vyvod, chto, k primeru, ob'ekt N klassificiruetsya kak zvezda K4V s pogreshnost'yu 1 spektral'nyi podklass s veroyatnost'yu 70%.

Vhodnye dannye dlya metoda maksimal'nogo pravdopodobiya takie zhe, kak i v predydushem sluchae, no vmesto minimizacii $\chi^2$ vychislyaetsya znachenie i proizvoditsya maksimizaciya tak nazyvaemoi funkcii pravdopodobiya :

$\begin{displaymath} -\ln{L}+const=\sum\limits_{i=1}^{N}\frac{(\alpha T_{i}-F_{i})^{2}}{2 \Delta F_{i}^{2}} \end{displaymath}$

(1.6)

S matematicheskoi tochki zreniya dannaya procedura absolyutno identichna minimizacii $\chi^2$ , razlichie zaklyuchaetsya lish' v oboznacheniyah.

1.2.2. Metody mnogomernoi polinomial'noi approksimacii

Principial'no drugim yavlyaetsya podhod k fotometricheskoi klassifikacii ob'ektov, ispol'zuyushii tak nazyvaemye trenirovochnye nabory dannyh, to est' fotometricheskie dannye dlya ob'ektov izvestnogo tipa (v chastnom sluchae krasnogo smesheniya) v teh zhe fil'trah. V kachestve trenirovochnogo nabora dannyh mozhno brat' rezul'taty modelirovaniya. Vnachale nekim obrazom proizvoditsya parametrizaciya raspredelenii energii v spektrah ob'ektov iz trenirovochnogo nabora. Zatem proizvoditsya approksimaciya zavisimosti iskomyh parametrov ob'ekta (tipa ob'ekta, krasnogo smesheniya, spektral'nogo klassa i t.p.) ot etih raspredelenii, obychno s pomosh'yu mnogomernogo polinomial'nogo fittinga. V rezul'tate mozhno opredelit' iskomye parametry dlya neizvestnogo ob'ekta, podstaviv parametrizaciyu ego SED v approksimaciyu dannoi zavisimosti.

Matematicheski dannaya zadacha dovol'no slozhna, i v nastoyashee vremya odin iz naibolee populyarnyh podhodov k ee resheniyu zaklyuchaetsya v ispol'zovanii iskusstvennyh neironnyh setei [23,24].

Neironnye seti neodnokratno uspeshno ispol'zovalis' v astronomii, v chastnosti, dlya morfologicheskoi klassifikacii galaktik [25], dlya morfologicheskogo razdeleniya zvezd i galaktik [21,22] i spektral'noi klassifikacii zvezd [26,27,28]. S matematicheskoi tochki zreniya neironnaya set' predstavlyaet soboi nelineinyi operator, deistvuya kotorym na vhodnye dannye, mozhno poluchit' rezul'tat opredelennogo vida na vyhode. Obychno neironnye seti dlya naglyadnosti predstavlyayut kak sovokupnost' neskol'kih urovnei - vhodnogo, odnogo ili bolee skrytyh i vyhodnogo. Pri etom kazhdyi uzel seti soedinen so vsemi uzlami predydushego urovnya i so vsemi uzlami sleduyushego urovnya. Arhitektura neironnoi seti mozhet byt' opisana sootnosheniem $N_{in}:N_1:N_2:\ldots:N_{out}$ , gde $N_{in}$ - chislo vhodnyh uzlov, $N_{i}$ - chislo uzlov na -m skrytom urovne i $N_{out}$ - chislo vyhodov. Kazhdaya svyaz' mezhdu uzlami imeet ves i vse oni dlya kazhdogo iz urovnei obrazuyut vektor vesovyh koefficientov.

Rassmotrim process poiska krasnogo smesheniya dlya vnegalakticheskih ob'ektov. Na vhod neironnoi seti podayutsya potoki ili -velichiny v kazhdom iz fil'trov, na vyhode poluchaetsya znachenie krasnogo smesheniya. Pered ispol'zovaniem neironnyh setei dlya polucheniya korrektnyh rezul'tatov neobhodimo provesti tak nazyvaemyi process trenirovki seti. Dlya etogo na vhod podayutsya dannye ih trenirovochnogo nabora, a na vyhod - izvestnoe . Togda v processe trenirovki neironnoi seti proizvoditsya ee optimizaciya pri pomoshi minimizacii ostatochnoi funkcii:

$\begin{displaymath} E = \frac{1}{2}\sum\limits_{k}[z_k-F(w,x_k)]^2 \end{displaymath}$

(1.7)

gde funkciya

zadaetsya set'yu. Peredatochnaya funkciya

, zadannaya v kazhdom uzle

, beret v kachestve argumenta

$\begin{displaymath} u_p=\sum\limits_{j}w_j x_j \end{displaymath}$

(1.8)

gde summa beretsya po vsem vhodnym uzlam dlya uzla

. Ona obychno vybiraetsya takim obrazom, chtoby vhodnoi argument mog prinimat' proizvol'nye znacheniya, a vyhodnye znacheniya lezhali by v strogo ogranichennom diapazone. Po analogii s biologiei v kachestve peredatochnoi funkcii obychno ispol'zuyut kakuyu-libo iz sigmoidnyh funkcii, k primeru $g_p(u_p)=1/[1+\exp{(-u_p)}]$ , to est' funkciyu, grafik kotoroi pohozh na bukvu

. Kombinaciya

po vsei seti formiruet funkciyu

. V processe trenirovki neironnoi seti neobhodimo delat' proverku rabotosposobnosti s pomosh'yu vyborki dannyh iz trenirovochnogo nabora, imeyushih te zhe statisticheskie harakteristiki, chto i dannye, ispol'zuemye dlya trenirovki; pri etom vesa svyazei zamorazhivayutsya [24].

Kak pokazano v rabotah [23,24] primenenie neironnyh setei dlya metoda, ispol'zuyushego trenirovochnye nabory dannyh, daet rezul'taty ne huzhe metodov minimizacii $\chi^2$ , a zachastuyu namnogo luchshe.

Esli neobhodimo proizvodit' veroyatnostnye ocenki, to est', naprimer, poluchit' plotnost' veroyatnosti ot krasnogo smesheniya, neobhodimo postroit' neironnuyu set' s bol'shim kolichestvom vyhodov, kazhdyi iz kotoryh budet sootvetstvovat' shagu po . Vo vremya trenirovki neobhodimo zadavat' "1" tol'ko na vyhode, sootvetstvuyushem pravil'nomu krasnomu smesheniyu, a na vseh ostal'nyh "0". Togda v rezul'tate primeneniya neironnoi seti k vhodnym dannym na kazhdom iz vyhodov budet poluchat'sya sootvetstvuyushee znachenie plotnosti veroyatnosti.

U metoda ispol'zuyushego neironnye seti est' odin dostatochno bol'shoi nedostatok - dazhe pri ispol'zovanii sovremennyh vychislitel'nyh sredstv vremya, zatrachivaemoe na trenirovku neironnoi seti, dostigaet neskol'kih chasov, v otlichie ot metoda minimizacii $\chi^2$ , pri pravil'noi realizacii kotorogo neskol'ko tysyach ob'ektov budut obrabotany men'she, chem za minutu.

1.3. Tretii uroven' obrabotki fotometricheskih dannyh - ispol'zovanie dopolnitel'nyh svedenii

Posle provedeniya vtorogo etapa obrabotki mozhet okazat'sya, chto chast' ob'ektov primerno ravnoveroyatno klassificiruetsya po razlichnym tipam i/ili krasnym smesheniyam. Pri etom v ryade sluchaev nekotorye varianty mozhno otbrosit', esli privlech' dopolnitel'nye svedeniya.

Naprimer, esli ob'ekt 18-i zvezdnoi velichiny ravnoveroyatno klassificiruetsya kak kvazar s krasnym smesheniem 4.0 i ellipticheskaya galaktika s krasnym smesheniem 3.9, to vtoroi variant fizicheski ne realizuem, esli prinyat' vo vnimanie rasstoyanie, opredelyaemoe po znacheniyu z, i diapazon svetimostei kvazarov i galaktik. Zdes' dopolnitel'noi informaciei sluzhat funkcii svetimosti sootvetstvuyushih tipov ob'ektov.

Drugim vidom dopolnitel'noi informacii yavlyaetsya morfologiya ob'ekta. Esli ob'ekt na pryamom snimke imeet protyazhennyi vid, a klassificiruetsya libo kak zvezda spektral'nogo klassa K, libo kak galaktika s nebol'shim krasnym smesheniem, to pervyi variant otbrasyvaetsya, tak kak zvezda dolzhna byt' tochechnym ob'ektom, to est' ee forma ne mozhet sil'no otlichat'sya ot srednei PSF po polyu.

Naibolee neodnoznachnoi yavlyaetsya situaciya, kogda slabyi ob'ekt klassificiruetsya kak zvezda i kak kvazar libo galaktika s bol'shim krasnym smesheniem. Zdes' morfologicheskii kriterii ne rabotaet, funkcii svetimosti dalekih ob'ektov izvestny ne ochen' horosho. No v sluchae esli nablyudaetsya pole na vysokih galakticheskih shirotah, mozhno nalozhit' ogranicheniya na yarkost' zvezd polya, prinimaya vo vnimanie zvezdnoe naselenie, kotoroe prisutstvuet na dannyh napravleniyah v Galaktike. Zdes' privoditsya tablica 1.1, v kotoroi soderzhitsya informaciya o razlichnyh tipah zvezd, kotorye mozhno vstretit' na vysokih galakticheskih shirotah. V pervoi kolonke soderzhitsya informaciya o spektral'nom klasse i klasse svetimosti zvezd, vo vtoroi - diapazon absolyutnyh zvezdnyh velichin v fil'tre V, v tret'ei - maksimal'noe rasstoyanie, na kotorom mozhno vstretit' dannye zvezdy, i v chetvertoi - minimal'nuyu yarkost', kotoruyu oni mogut imet'.

Tablica 1.1. Nizhnie predely na yarkost' zvezd, nablyudaemyh na vysokih galakticheskih shirotah

Sp, Lum	M	R, kpc	$m_{lim}$	Sp, Lum	M	R, kpc	$m_{lim}$
OI-V	-4..-9	0.5	4	FV-VI	5..1	0.5	13
BI-V	0..-8	0.5	8	GV-VI	7..3	25	24
AI-IV	-1..-8	0.5	7	KV-VI	9..5	25	26
FI-IV	0..-7	25	17	MV-VI	17..8	25	30
GI-IV	2..-7	25	19	LV	17	25	30
KI-IV	4..-7	25	21	WD	16..8	25	30
MI-IV	4..-7	25	21	PLN*	8..0	25	25
AV-VI	3..-1	0.5	11

Ispol'zuya dannye iz tablicy, v nekotoryh sluchayah mozhno uverenno otdelit' zvezdy ot dalekih galaktik i kvazarov. K primeru, esli ob'ekt klassificiruetsya primerno ravnoveroyatno kak dalekii ob'ekt i kak zvezda, i pri etom ego yarkost' sushestvenno slabee znacheniya iz tret'ei kolonki tablicy, to predpochtenie otdaetsya pervomu variantu klassifikacii.

<< Vvedenie | Oglavlenie | 2. Biblioteka template-spektrov >>

Publikacii s klyuchevymi slovami: galaktika - Spektr - kvazary - Seifertovskaya galaktika Publikacii so slovami: galaktika - Spektr - kvazary - Seifertovskaya galaktika
Sm. takzhe: M106: spiral'naya galaktika so strannym yadrom Tri galaktiki v Drakone Solnce i propavshie cveta V rukavah NGC 1097 Blizkaya spiral'naya galaktika NGC 4945 Kvazar v rannei Vselennoi Kometa Leonarda i galaktika Kit Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce