Gidromagnitnoe dinamo

GIDROMAGNITNOE DINAMO - mehanizm usileniya ili podderzhaniya stacionarnogo (libo kolebatel'nogo) sostoyaniya magn. polya gidrodinamich. dvizheniyami provodyashei sredy.

Bol'shinstvo kosmich. tel (planety, zvezdy, galaktiki) i okruzhayushaya ih sreda obladayut magn. polyami. Proishozhdenie i nablyudaemye izmeneniya kosmich. magn. polei svyazany, kak pravilo, s dvizheniyami plazmy. Ideyu o tom, chto dvizheniya plazmy mogut privodit' k usileniyu magn. polya, vydvinul angl. fizik Dzh. Larmor v 1919 g. Nazvanie G. d. vozniklo iz-za shozhesti processa s rabotoi dinamo-mashiny. Osobennost' G. d. sostoit v tom, chto ono dolzhno byt' samovozbuzhdayushimsya, t. e. ne podderzhivayushimsya za schet vnesh. istochnikov polya. V teoretich. issledovaniyah prinyato govorit' o probleme kinematich. G. d., k-ruyu mozhno sformulirovat' sled. obrazom. Pust' v ob'eme plazmy s zadannoi provodimost'yu podderzhivayutsya k.-l. dvizheniya plazmy i sozdano slaboe magn. pole, ne podderzhivaemoe dalee vnesh. istochnikami. Esli so vremenem pole i polnaya magnitnaya energiya rassmatrivaemogo ob'ema ne ubyvayut, nesmotrya na deistvie omicheskoi dissipacii, to imeet mesto G. d.

Teoriya G. d. yavl. vetv'yu magnitogidrodinamiki. Relyativistskie effekty, toki smesheniya, v teorii G. d. obychno ne uchityvayutsya. V etom smysle magn. pole ne zavisit ot sistemy otscheta i mozhno pol'zovat'sya predstavleniem o magn. silovyh liniyah.

Vozmozhnost' usileniya nachal'nogo (zatravochnogo) magn. polya dvizheniyami sredy svyazana s t. n. vmorozhennost'yu polya v plazmu (sm. Magnitogidrodinamika). Delo v tom, chto harakternye razmery L oblastei, zanimaemyh kosmich. telami, obychno stol' veliki, chto dazhe pri umerennoi provodimosti plazmy s harakternye vremena t omicheskogo zatuhaniya polya ogromny:

t = 4psL²/c² є L²/v_m,

gde v_m є c²/4ps- magnitnaya vyazkost' (formuly dany v gaussovoi sisteme edinic). Poetomu magnitnye silovye linii prakticheski "prikleeny" k dvizhusheisya provodyashei srede, kotoraya uvlekaet za soboi pole. Esli silovaya liniya prohodila cherez k.-l. dve blizkie chasticy sredy, to ona budet prohodit' cherez nih i v dal'neishem. V usloviyah vmorozhennosti proizvedenie indukcii V magn. polya na ploshad' lyubogo dvizhushegosya so sredoi kontura (magnitnyi potok) sohranyaetsya, chto mozhet privesti k usileniyu magn. polya pri deformacii (napr., pri szhatii) kontura. S drugoi storony, dvizheniya mogut zaputyvat' silovye linii polya, umen'shaya ego harakternye masshtaby i usilivaya tem samym dissipaciyu.

Otnositel'naya rol' usileniya polya dvizheniyami plazmy i dissipativnogo effekta opredelyaetsya bezrazmernym otnosheniem Lv/v_m є Rm - magn. chislom Reinol'dsa (v - harakternaya skorost' dvizhenii). Neobhodimoe uslovie raboty G. d. obychno zaklyuchaetsya v tom, chtoby R_m prevyshalo nek-roe znachenie R_{m kritich} 10. V kosmich. plazme R_m, kak pravilo, ochen' veliko, i etot kriterii vypolnen s bol'shim zapasom. K dostatochnym usloviyam raboty G. d. otnositsya ryad ogranichenii na geometricheskie, tochnee topologicheskie, sv-va techeniya. Eti ogranicheniya dostatochno polno ustanovleny dlya sluchaya, kogda rassmatrivaetsya povedenie magn. polya pri zadannom techenii plazmy (kinematich. dinamo). V chastnosti, G. d. nevozmozhno, kogda dvizhenie proishodit vdol' sferich. ili ploskih poverhnostei. Pri dvizheniyah provodyashei sredy vdol' poverhnostei dr. tipov, napr, cilindricheskih ili toroidal'nyh, G. d. vozmozhno. Magn. pole pri etom (esli prenebrech' ego vliyaniem na dvizhenie) rastet eksponencial'no. Odnako skorost' rosta polya okazyvaetsya maloi v sluchae bol'shih R_m (medlennoe dinamo). Takoe dinamo v principe mozhet rabotat' v yadrah planet, gde R_m otnositel'no neveliki: v zemnom yadre R_m »150. Poskol'ku dlya bol'shinstva kosmich. ob'ektov znacheniya R_m ochen' veliki (napr., v solnechnoi konvektivnoi zone R_m~10⁸), principial'no vazhno otvetit' na vopros, sushestvuet li bystroe dinamo so skorost'yu rosta, ne stremyasheisya k nulyu (ili k otricat. znacheniyu) pri R_m >> 1.

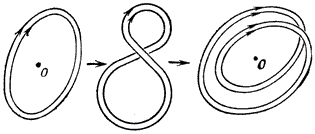
Ris. 1. Usilenie magnitnogo polya putem perekruchivaniya i udvoeniya petel': dvizheniya sredy pridayut liniyam nachal'nogo toroidal'nogo magnitnogo polya formu vos'merki, zatem sovmeshayut petli vos'merki i rastyagivayut poluchivshiisya tor do nachal'nyh razmerov. Posle etogo process povtoryaetsya. Pri kazhdom udvoenii chisla petel' proishodit dvukratnoe usilenie magnitnogo polya.

Primer bystrogo dinamo, predlozhennyi Ya. B. Zel'dovichem, pokazan na ris. 1.

Bystroe dinamo mozhet rabotat' v tipichnoi dlya kosmich. uslovii turbulentnoi srede. V to zhe vremya turbulentnye dvizheniya zaputyvayut magn. silovye linii, umen'shaya ih harakternyi masshtab. Dlya usileniya i podderzhaniya krupnomasshtabnyh magn. polei turbulentnye dvizheniya ne dolzhny obladat' zerkal'noi simmetriei. Narushenie zerkal'noi simmetrii oznachaet preobladanie vihrei odnogo znaka (pravovintovyh ili levovintovyh), t. e. nalichie sr. spiral'nosti. Takaya turbulentnost' ne tipichna dlya laboratornyh eksperimentov, odnako estestvennym obrazom voznikaet v kosmich. usloviyah blagodarya vrasheniyu neodnorodnyh nebesnyh tel. Kak pokazali teoretich. issledovaniya, zerkal'no-nesimmetrichnye sluchainye dvizheniya sposobny generirovat' krupnomasshtabnoe magn. pole.

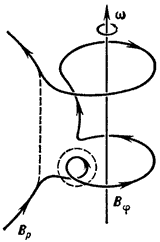Ris. 2. Generaciya magnitnogo polya v sluchae neodnorodnogo vrasheniya plazmy. V rezul'tate nakruchivaniya vmorozhennyh magnitnyh silovyh linii iz ishodnogo poloidal'nogo  (meridional'nogo) polya Vr obrazuetsya azimutal'noe pole Vj. Shtrihovym kruzhkom otmechena odna petlya, sozdannaya turbulentnymi dvizheniyami (ona izobrazhena na ris. 3).

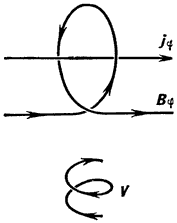Ris. 3. Gidromagnitnoe dinamo pri nalichii srednei spiral'nosti dvizhenii plazmy. Preobladanie techenii ukazannogo na risunke (vnizu) tipa (levo- ctoronnyaya spiral') privodit k poyavleniyu elektricheskogo toka jj, parallel'nogo magnitnomu polyu Bj. Takoi tok v svoyu ochered' sozdaet magnitnoe pole, perpendikulyarnoe ishodnomu polyu. Povtornoe pri- menenie effekta k novomu polyu pozvolyaet sozdat' pole, parallel'noe (ili antiparallel'- noe) ishodnomu, t. e. privodit k samovozbuzhdeniyu sistemy.

Effekty generacii magn. polya blagodarya neodnorodnomu (differencial'nomu) vrasheniyu i spiral'nosti turbulentnosti sostavlyayut osnovu teorii turbulentnogo G. d. krupnomasshtabnyh magn. polei. Eta teoriya ispol'zuetsya pri reshenii ryada astrofizich. zadach: generaciya magn. polei v yadrah planet, v diskah dvoinyh rentg. istochnikov, v galaktich. diske, sushestvovanie solnechnogo cikla i dr. Differencial'noe vrashenie v provodyashei srede s magn. polem v meridional'noi (soderzhashei os' vrasheniya) ploskosti privodit k poyavleniyu (nakruchivaniyu) azimutal'nogo (perpendikulyarnogo meridional'noi ploskosti v dannoi tochke) polya (ris. 2). Turbulentnye dvizheniya sozdayut i zakruchivayut petli azimutal'nogo polya. Kogda imeetsya preimushestvennoe napravlenie zakruchivaniya (sr. spiral'nost' turbulentnosti), poyavlyaetsya sr. tok, parallel'nyi azimutal'nomu magn. polyu i, sledovatel'no, porozhdayushii novuyu meridional'nuyu sostavlyayushuyu polya (ris. 3). Sovokupnoe deistvie etih dvuh effektov ili dazhe tol'ko vtorogo pri podhodyashih usloviyah privodit k samovozbuzhdeniyu polya, t. e. k G. d.

V dopolnenie k ukazannym dvum effektam krupnomasshtabnoe pole podvergaetsya turbulentnoi diffuzii, k-raya gorazdo effektivnee omicheskoi. Krome togo, neodnorodnaya (v chastnosti, u granic) turbulizovannaya provodyashaya sreda s bol'shim R_m vedet sebya podobno diamagnetiku, t. e. krupnomasshtabnoe magn. pole vytalkivaetsya iz turbulentnoi oblasti. K vytalkivaniyu magn. silovyh linii privodyat i krupnomasshtabnye techeniya plazmy s zamknutymi liniyami toka. Svoeobraznyi effekt vytesneniya polya vozmozhen v yacheistoi konvekcii, v k-roi zhidkost' podnimaetsya v centre yacheiki i opuskaetsya u ee granic.

Bol'shoi interes dlya kosmich. fiziki predstavlyaet vopros o G. d. melkomasshtabnyh fluktuacionnyh polei. Srednekvadratichnye znacheniya etih polei, kak pravilo, prevyshayut velichinu krupnomasshtabnogo sr. polya. Pri turbulentnom dvizhenii so sr. spiral'noet'yu i bez nee (s uchetom vliyaniya polya na dvizhenie) G. d. melkomasshtabnyh polei vozmozhno. Pri nalichii sr. spiral'nosti magn. polya generiruyutsya vo vseh masshtabah, prevyshayushih dissipacionnyi, prichem s techeniem vremeni proishodit sdvig "centra tyazhesti" generiruemyh polei v storonu bol'shih masshtabov (effektivnost' generacii rastet s masshtabom polya).

V teoretich. rabotah mnogo vnimaniya udelyaetsya postroeniyu modelei G. d. dlya laminarnyh techenii plazmy. Pervym primerom takogo dinamo byla model' samovozbuzhdeniya magn. polya v sisteme, sostoyashei iz dvuh sfer, vrashayushihsya vokrug neparallel'nyh osei i pogruzhennyh v sredu s konechnoi provodimost'yu. Postroeny tochnye resheniya ur-nii G. d. dlya sistemy iz dvuh toroidal'nyh vihrei, vintovogo dvizheniya vdol' cilindrich. poverhnosti i mn. dr. Idei laminarnogo G. d. ispol'zuyutsya pri ob'yasnenii proishozhdeniya magn. polei v planetah i dvoinyh zvezdnyh sistemah. Vedutsya issledovaniya s cel'yu postroeniya laboratornoi modeli G. d.

Lit.: Pikel'ner S. B., Osnovy kosmicheskoi elektrodinamiki, 2 izd., M., 1966;
Moffat G., Vozbuzhdenie magnitnogo polya v provodyashei srede, per, s angl., M., 1980;
Vainshtein S. I., Zel'dovich Ya. B., Ruzmaikin A. A., Turbulentnoe dinamo v astrofizike, M., 1980;
Parker E. N., Kosmicheskie magnitnye polya, per. s angl., M., 1982;
Krauze F., Redler K. - X., Magnitnaya gidrodinamika srednih polei i teoriya dinamo, per. s angl., M., 1984;
Bochkarev N. G., Magnitnye polya v kosmose, M., 1985.

(A.A. Ruzmaikin)