Gravitacionnyi kollaps
GRAVITACIONNY' KOLLAPS
Soderzhanie:
1. Vvedenie
2. Usloviya gidrostaticheskogo
ravnovesiya zvezdy n vozniknovenie
gravitacionnogo kollapsa
3. Dinamika gravitacionnogo
kollapsa zvezd s razlichnymi massami
zheleznogo yadra (![]() ).
).
4. Termoyadernyi vzryv uglerodno-kislorodnyh
zvezd (![]() ) i razvitie
gravitacionnogo kollapsa
) i razvitie
gravitacionnogo kollapsa
5. Vspyshki sverhnovyh zvezd,
statistika kollapsiruyushih zvezd,
vozmozhnosti nablyudenii
G. k. zvezdy - katastroficheski bystroe ee
szhatie pod deistviem sobstv. sil tyagoteniya -
mozhet proizoiti posle prekrasheniya v centr.
oblasti zvezdy termoyadernyh reakcii. S
istosheniem v zvezde zapasov yadernoi
energii i ugasaniem central'nogo istochnika
energii neposredstvenno narushaetsya ee
teplovoe, a zatem i gidrostaticheskoe (mehanich.)
ravnovesie. Pri etom oslablyayutsya sily,
protivodeistvuyushie tyagoteniyu, i voznikayut
usloviya dlya bystrogo szhatiya zvezdy. G. k.
rassmatrivayut kak odin iz vozmozhnyh putei
zaversheniya evolyucii
zvezd (s ![]() ),
privodyashei k obrazovaniyu neitronnyh zvezd
ili dazhe (v sluchae relyativistskogo G. k.)
chernyh dyr. Vybros vnesh. sloev zvezdy,
vozmozhnyi pri G. k. ee centr. oblasti,
privodit k poyavleniyu sverhnovoi zvezdy.
),
privodyashei k obrazovaniyu neitronnyh zvezd
ili dazhe (v sluchae relyativistskogo G. k.)
chernyh dyr. Vybros vnesh. sloev zvezdy,
vozmozhnyi pri G. k. ee centr. oblasti,
privodit k poyavleniyu sverhnovoi zvezdy.
Termoyadernye reakcii sluzhat istochnikom
energii zvezdy i obespechivayut v nei
gidrostatich. i teplovoe ravnovesie vplot'
do obrazovaniya v ee centr. oblasti atomnyh
yader gruppy zheleza. .Eti yadra imeyut
naibol'shuyu energiyu
svyazi na nuklon, tak chto
sintez yader bolee tyazhelyh, chem yadra zheleza,
uzhe ne soprovozhdaetsya vydeleniem energii, a,
naoborot, trebuet zatrat energii. Lishennaya
s etogo momenta termoyadernyh istochnikov
energii, zvezda ne mozhet skompensirovat'
poteri energii vo vneshnee prostranstvo, tem
bolee chto k koncu "termoyadernogo"
etapa evolyucii eti poteri chrezvychaino
vozrastayut. K obychnym poteryam energii s
poverhnosti zvezdy (ispuskaniyu fotonov
fotosferoi zvezdy) zdes' pribavlyayutsya
ob'emnye poteri energii, obuslovlennye
intensivnym izlucheniem neitrino
(v) i antineitrino (![]() ) centr. oblast'yu zvezdy.
Ob'emnye poteri energii, kak pokazyvayut
raschety evolyucii zvezd, stanovyatsya
preobladayushimi nad poteryami s poverhnosti
pri temp-pax v centre zvezdy
) centr. oblast'yu zvezdy.
Ob'emnye poteri energii, kak pokazyvayut
raschety evolyucii zvezd, stanovyatsya
preobladayushimi nad poteryami s poverhnosti
pri temp-pax v centre zvezdy ![]() . Dlya
pozdnei stadii yadernoi evolyucii dostatochno
massivnoi zvezdy eto uslovie vypolnyaetsya s
izbytkom - pri sinteze yader gruppy zheleza
temp-pa v centre zvezdy s
. Dlya
pozdnei stadii yadernoi evolyucii dostatochno
massivnoi zvezdy eto uslovie vypolnyaetsya s
izbytkom - pri sinteze yader gruppy zheleza
temp-pa v centre zvezdy s ![]() dostigaet 3.109K. U malomassivnyh zvezd, s
massoi okolo nizhnego predela
dostigaet 3.109K. U malomassivnyh zvezd, s
massoi okolo nizhnego predela ![]() , temp-pa
v centre v konce yadernoi evolyucii tozhe
dostigaet znacheniya
, temp-pa
v centre v konce yadernoi evolyucii tozhe
dostigaet znacheniya ![]() i ob'emnye
poteri energii v vide neitrinnogo
izlucheniya stanovyatsya osnovnymi.
i ob'emnye
poteri energii v vide neitrinnogo
izlucheniya stanovyatsya osnovnymi.
Neskompensirovannye poteri energii narushayut ravnovesie zvezdy. Sozdayutsya usloviya dlya szhatiya ee centr. oblasti pod deistviem sobstv. sil tyagoteniya. Zvezda rashoduet teper' gravitacionnuyu energiyu, vydelyayushuyusya pri szhatii. Temp-pa v szhimayusheisya zvezde vozrastaet (sm. Viriala teorema). Snachala szhatie zvezdy idet medlenno, tak chto uslovie gidrostatich. ravnovesiya eshe vypolnyaetsya. Nakonec, temp-ra dostigaet takih vysokih znachenii, »(5-10).109K, chto yadra gruppy zheleza teryayut ustoichivost'. Oni raspadayutsya na yadra geliya, neitrony i protony (na pervom etape raspada 5626Fe ® 1342He + 4n - 124,4 MeV, a pri dal'neishem roste temp-ry raspadayutsya i yadra Ne: 42Ne ® 2n + 2r - 26,21MeV). Raspad yader trebuet znachit. zatrat energii, t. k. predstavlyaet soboi kak by vsyu cep' termoyadernyh reakcii sinteza ot vodoroda do zheleza, no idushuyu v obratnom napravlenii (ne s vydeleniem, a s poglosheniem energii). Temp-pa v nedrah zvezdy vse zhe rastet (za schet gravitac. szhatiya), no iz-za raspada yader zheleza, trebuyushego zatrat energii, ne tak bystro, kak eto bylo by neobhodimo dlya priostanovleniya szhatiya. V rezul'tate poter' energii na neitrinnoe izluchenie i raspada yader proishodit svoeobraznyi vzryv zvezdy - vzryv vnutr' (inogda v nauchnoi literature ego naz. imploziei, v otlichie ot eksplozii - vzryva naruzhu, vyzvannogo bystrym vysvobozhdeniem energii). Pri implozii veshestvo centr. oblasti zvezdy padaet k centru so skorost'yu, blizkoi k skorosti svobodnogo padeniya. Voznikayushaya pri etom gidrodinamicheskaya volna razrezheniya vtyagivaet posledovatel'no v rezhim padeniya vse bolee udalennye ot centra sloi zvezdy. Nachavshiisya G. k. pri opredelennyh usloviyah mozhet zatormozit'sya ili dazhe ostanovit'sya, no v ryade sluchaev mozhet bezostanovochno prodolzhat'sya, perehodya v t. n. relyativistskii gravitacionnyi kollaps.
Vyyasnenie vsego kompleksa uslovii, privodyashih k G. k.,- zadacha kraine slozhnaya. Odin iz vazhnyh etapov resheniya etoi zadachi - issledovanie uslovii gidrostatich. ravnovesiya na pozdnih stadiyah evolyucii zvezdy s privlecheniem ur-niya sostoyaniya veshestva v zvezde.
2. Usloviya gidrostaticheskogo ravnovesiya zvezdy i vozniknovenie gravitacionnogo kollapsa
Na vsem protyazhenii evolyuc. razvitiya
zvezdy, svyazannogo s termoyadernymi
reakciyami v ee centr. oblasti, v zvezde za
redkim isklyucheniem podderzhivaetsya
gidrostatich. ravnovesie. Ono zaklyuchaetsya v
ravenstve (v kazhdoi tochke zvezdy i v lyuboi
moment vremeni) sil tyagoteniya ![]() i
sil ottalkivaniya chastic veshestva,
obuslovlennyh davleniem r, F-= -Dr/Dr [zdes'
figuriruyut abs. velichiny etih sil, r -
rasstoyanie ot centra do rassmatrivaemoi
tochki zvezdy,
i
sil ottalkivaniya chastic veshestva,
obuslovlennyh davleniem r, F-= -Dr/Dr [zdes'
figuriruyut abs. velichiny etih sil, r -
rasstoyanie ot centra do rassmatrivaemoi
tochki zvezdy, ![]() - massa vnutri sfery
radiusa r, r - plotnost' veshestva, -Dr/Dr -
priblizhennoe vyrazhenie radial'noi
sostavlyayushei gradienta davleniya v
okrestnosti rassmatrivaemoi tochki].
Usrednennoe dlya vsei zvezdy v celom ur-nie
gidrostatich. ravnovesiya mozhno priblizhenno
zapisat' v vide:
- massa vnutri sfery
radiusa r, r - plotnost' veshestva, -Dr/Dr -
priblizhennoe vyrazhenie radial'noi
sostavlyayushei gradienta davleniya v
okrestnosti rassmatrivaemoi tochki].
Usrednennoe dlya vsei zvezdy v celom ur-nie
gidrostatich. ravnovesiya mozhno priblizhenno
zapisat' v vide:
![]()
gde ![]() i R - polnaya massa i radius zvezdy,
rs
i rs - plotnost' i davlenie v centre zvezdy.
Eto ur-nie pozvolyaet, v chastnosti, ocenit'
temp-ru Ts okolo centra zvezdy. Esli prinyat',
chto veshestvo tam podchinyaetsya ur-niyu
sostoyaniya ideal'nogo gaza, to
i R - polnaya massa i radius zvezdy,
rs
i rs - plotnost' i davlenie v centre zvezdy.
Eto ur-nie pozvolyaet, v chastnosti, ocenit'
temp-ru Ts okolo centra zvezdy. Esli prinyat',
chto veshestvo tam podchinyaetsya ur-niyu
sostoyaniya ideal'nogo gaza, to
![]() , gde m
- molekulyarnaya massa veshestva zvezdy, R0
- universal'naya gazovaya postoyannaya. Dlya
zvezd tipa Solnca Ts~107K, dlya
kollapsiruyushih (bolee massivnyh) zvezd ona
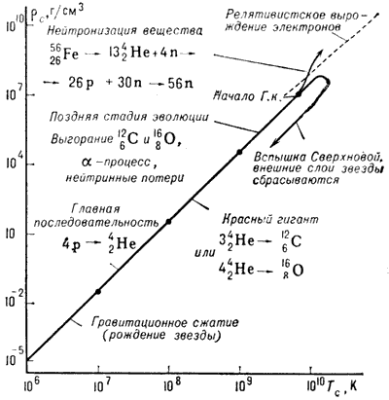
gorazdo vyshe. Na ris. 1 pokazana vozmozhnaya
shema evolyuc. puti massivnoi zvezdy (
, gde m
- molekulyarnaya massa veshestva zvezdy, R0
- universal'naya gazovaya postoyannaya. Dlya
zvezd tipa Solnca Ts~107K, dlya
kollapsiruyushih (bolee massivnyh) zvezd ona
gorazdo vyshe. Na ris. 1 pokazana vozmozhnaya
shema evolyuc. puti massivnoi zvezdy (![]() ) ot momenta ee rozhdeniya iz gazovo-pylevogo
oblaka do momenta polnogo istosheniya v ee
centr. oblasti termoyadernogo topliva i
nastupleniya G. k. (tochka razvetvleniya).
) ot momenta ee rozhdeniya iz gazovo-pylevogo
oblaka do momenta polnogo istosheniya v ee
centr. oblasti termoyadernogo topliva i
nastupleniya G. k. (tochka razvetvleniya).
 |
|
Ris. 1. Evolyucionnyi put' zvezdy s |
Evolyuciya zvezdy posle "vyklyucheniya" termoyadernyh istochnikov energii, strogo govorya, mozhet idti dvumya putyami: pri sohranenii gidrostatich. ravnovesiya i gidrodinamich. putem, kogda sily tyagoteniya stanut sushestvenno preobladayushimi (F+>F-). Put', po k-romu poidet evolyuciya zvezdy, zavisit ot togo, kak davlenie veshestva zvezdy izmenyaetsya s izmeneniem temp-ry i plotnosti, t. e. ot ur-niya sostoyaniya veshestva. Esli uvelichenie plotnosti pri szhatii veshestva silami tyagoteniya ne soprovozhdaetsya dostatochno intensivnym rostom davleniya, to v zvezde sozdayutsya predposylki dlya narusheniya gidrostatich. ravnovesiya i razvitiya G. k. Svyaz' davleniya s plotnost'yu v sluchae bystrogo szhatiya veshestva (imeyushego harakter adiabaticheskogo processa) imeet vid: rs ~ rgc (g nazyvaetsya pokazatelem adiabaty).
V svoyu ochered', plotnost' veshestva opredelyaetsya razmerami zvezdy rc ~ 1/R3. Vyrazhenie dlya sil ottalkivaniya mozhet byt' zapisano, sledovatel'no, v vide:
![]()
Zavisimost' sil tyagoteniya ot radiusa zvezdy daetsya sootnosheniem:
![]()
Iz sootnoshenii (2) i (3) vidno, chto sily tyagoteniya bystree narastayut s umen'sheniem radiusa zvezdy po sravneniyu s silami davleniya, esli
5 > 1 + 3g ili g < 4/3 (4),
Pri g < 4/3 lyuboe sluchainoe maloe gidrodinamich. vozmushenie tipa szhatiya budet narastat'. Uprugost' veshestva v etom sluchae nedostatochna dlya predotvrasheniya G. k. V protivnom sluchae (pri g > 4/3) gidrostatich. ravnovesie ustoichivo: sluchaino voznikshie uplotneniya budut rassasyvat'sya i zatuhat'. V strogoi teorii gidrostatich. ustoichivosti zvezd uchityvayut neodinakovost' g dlya razlichnyh sloev zvezdy. Fakticheski usloviya G. k. nastupayut, kogda v centr. oblasti g < 4/3, a vo vnesh. sloyah eshe vypolnyaetsya uslovie g > 4/3. Na ris. 2 privedeny rezul'taty teoretich. raschetov velichiny g v zavisimosti ot plotnosti i temp-ry veshestva. Provedennye linii urovnya g = 4/3 otchetlivo vydelyayut "ovrag neustoichivosti" (oblast' s g < 4/3). Kogda v processe evolyucii v "ovrag neustoichivosti" popadaet znachit. chast' centr. oblasti zvezdy, nachinaetsya ee G. k.
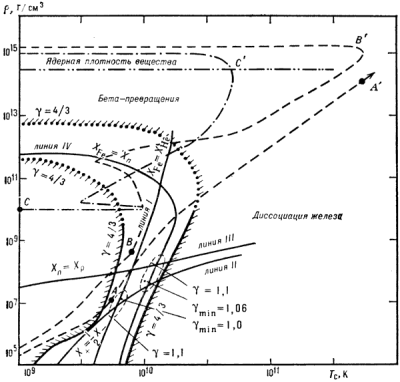 |
Ris. 2. Diagramma vzaimnyh prevrashenii
razlichnyh chastic zvezdnogo veshestva i ego
uprugih svoistv v zavisimosti ot plotnosti
(r) i temp-ry (Ts). Oblasti naimen'shei
uprugosti veshestva (s pokazatelem adiabaty gmin = 1 ,0
i 1,06) lezhat vblizi peresecheniya linii ravnyh
vesovyh koncentracii X: I - yader zheleza i
geliya (sleva ot linii preobladayut yadra
zheleza, sprava - geliya, na samoi linii XFe=XHe); II - elektron-pozitronnyh par i
atomnyh elektronov (vyshe etoi linii
preobladayut elektrony); III - neitronov i
protonov (vyshe linii preobladayut neitrony);
IV - yader zheleza i neitronov (vyshe i pravee
linii preobladayut neitrony). Na diagramme
izobrazheny puti central'nyh tochek zvezd: s
massoi |
3. Dinamika gravitacionnogo kollapsa
zvezd s razlichnymi massami zheleznogo yadra
(![]() )
)
Vyyavlenie fiz. processov, privodyashih k znacheniyam pokazatelya g < 4/3 predstavlyaet soboi odnu iz vazhnyh problem teorii G. k. Pri vysokih temp-pax i davleniyah, harakternyh dlya stadii polnogo prekrasheniya termoyadernyh reakcii v zvezde, plotnost' veshestva v centre zvezdy prevyshaet v milliony ili dazhe v milliardy raz plotnost' tverdyh tel na poverhnosti Zemli. Nesmotrya na eto, zvezdnoe veshestvo po sv-vam blizko k ideal'nomu gazu, t. k. kinetich. energiya obrazuyushih ego chastic znachitel'no prevyshaet potenc. energiyu ih vzaimodeistviya. Ot obychnogo ideal'nogo gaza veshestvo centr. oblasti zvezdy otlichaetsya tem, chto obrazuyushie ego raznorodnye chasticy (fotony, elektrony, pozitrony, protony, neitrony i raznoobraznye slozhnye atomnye yadra) pri vzaimodeistvii mogut ispytyvat' razlichnye prevrasheniya. Pri stolknovenii elektrona s pozitronom proishodit ih annigilyaciya, i rozhdayutsya fotony. V svoyu ochered', fotony vysokih energii pri stolknovenii s dr. chasticami mogut rozhdat' pary elektron - pozitron ili putem fotoyadernyh reakcii vyzyvat' dissociaciyu slozhnyh yader. Protony i neitrony uchastvuyut v raznoobraznyh yadernyh reakciyah so slozhnymi yadrami, k-rye takzhe mogut vzaimodeistvovat' mezhdu soboi. Nuklony i yadra ispytyvayut eshe razlichnye beta-prevrasheniya (sm. Beta-processy). Podobnye vzaimnye prevrasheniya chastic pri opredelennoi dostatochno vysokoi temp-re dostigayut dinamich. ravnovesiya (yadernogo statistich. ravnovesiya), i eto sostoyanie opredelyaet ravnovesnye koncentracii vseh chastic i vse sv-va zvezdnogo veshestva, v t. ch. granicy i glubinu "ovraga neustoichivosti".
Naryadu s prevrasheniyami chastic, k-rye
protekayut s ravnoi veroyatnost'yu v pryamom i
obratnom napravleniyah (tak chto oni
uravnoveshivayut drug druga), v konce
termoyadernoi stadii evolyucii zvezd znachit.
intensivnosti dostigayut beta-prevrasheniya.
V beta-prevrasheniyah obyazatel'no uchastvuyut
neitrino i antineitrino, k-rye srazu zhe
posle svoego rozhdeniya pokidayut zvezdu (dlya
nih tolsha zvezdy prozrachna). Poetomu beta-prevrasheniya
imeyut odnostoronnii harakter - reakcii
vzaimodeistviya neitrino i antineitrino s k.-l.
drugimi chasticami (napr., zahvat neitrino
protonom) v zvezde ne proishodit.
Odnostoronnii harakter beta-prevrashenii
oznachaet, chto v zvezdnom veshestve net
polnogo termodinamicheskogo ravnovesiya.
Kolichestvenno vklad beta-prevrashenii
osobenno sushestven v levoi verhnei chasti
"ovraga neustoichivosti", kuda mogut
popast' menee massivnye zvezdy, s ![]() .
Iz-za otsutstviya termodinamich. ravnovesiya
izobrazhennye v etoi chasti ris. 2 linii nosyat
uslovnyi harakter (oni byli fakticheski
vychisleny s ispol'zovaniem ves'ma grubogo
priblizheniya). Strogoe opredelenie fiz.
uslovii pri sushestvennom vklade beta-prevrashenii
trebuet posledovatel'nogo rascheta ih
kinetiki, samosoglasovannogo s raschetom
evolyucii i G. k. zvezdy. Tem ne menee moglo by
ustanavlivat'sya t. n. kinetich. ravnovesie, v k-rom uravnoveshivalis' by vse beta-prevrasheniya,
za isklyucheniem teh, k-rye mogli by byt'
vyzvany svobodno uletayushimi neitrino i
antineitrino. Pri takom ravnovesii dlya
bystryh gidrodinamicheskih vozmushenii, za
kotorymi ne pospevayut beta-prevrasheniya, "ovrag
neustoichivosti" meleet i suzhaetsya. A eto
oznachaet, chto mogut razvivat'sya tol'ko
neustoichivosti s harakternym vremenem beta-prevrashenii.
Poetomu u malomassivnyh zvezd G. k. dolzhen
razvivat'sya sravnitel'no medlenno. V obshem
sluchae zadachu razvitiya G. k. sleduet reshat'
s uchetom kinetiki vseh beta-prevrashenii.
.
Iz-za otsutstviya termodinamich. ravnovesiya
izobrazhennye v etoi chasti ris. 2 linii nosyat
uslovnyi harakter (oni byli fakticheski
vychisleny s ispol'zovaniem ves'ma grubogo
priblizheniya). Strogoe opredelenie fiz.
uslovii pri sushestvennom vklade beta-prevrashenii
trebuet posledovatel'nogo rascheta ih
kinetiki, samosoglasovannogo s raschetom
evolyucii i G. k. zvezdy. Tem ne menee moglo by
ustanavlivat'sya t. n. kinetich. ravnovesie, v k-rom uravnoveshivalis' by vse beta-prevrasheniya,
za isklyucheniem teh, k-rye mogli by byt'
vyzvany svobodno uletayushimi neitrino i
antineitrino. Pri takom ravnovesii dlya
bystryh gidrodinamicheskih vozmushenii, za
kotorymi ne pospevayut beta-prevrasheniya, "ovrag
neustoichivosti" meleet i suzhaetsya. A eto
oznachaet, chto mogut razvivat'sya tol'ko
neustoichivosti s harakternym vremenem beta-prevrashenii.
Poetomu u malomassivnyh zvezd G. k. dolzhen
razvivat'sya sravnitel'no medlenno. V obshem
sluchae zadachu razvitiya G. k. sleduet reshat'
s uchetom kinetiki vseh beta-prevrashenii.
V lyubom sluchae veshestvo zvezdy, popadaya v
"ovrag neustoichivosti", teryaet
uprugost', i zvezda, v konechnom schete, ne
mozhet protivodeistvovat' silam tyagoteniya,
chto vedet k razvitiyu G. k. Strogie raschety
dlya zvezdy s massoi ![]() (massa zheleznogo
yadra
(massa zheleznogo
yadra ![]() , ostal'noe - kislorodnaya
vnesh. obolochka) pokazyvayut ostanovku G. k.
pri dostizhenii v centre zvezdy plotnosti rs
~ 1013 g/sm3 i temp-ry Ts ~ 1011K. Posle ostanovki G.
k. nachinaetsya process obrazovaniya goryachei
neitronnoi zvezdy. Pri etom prodolzhaetsya
dovol'no medlennoe uvelichenie (vsya bystraya
stadiya G. k. do ostanovki harakterizuetsya
gidrodinamich. vremenem ~0,1 s) centr.
plotnosti do rs~1015 g/sm3 i temp-ry
Ts ~ 1012K (za
vremya »3s). Zatem proishodit eshe bolee
medlennyi process ohlazhdeniya goryachei
neitronnoi zvezdy, zavershayushiisya
obrazovaniem holodnoi neitronnoi zvezdy,
dlya k-roi massa
, ostal'noe - kislorodnaya
vnesh. obolochka) pokazyvayut ostanovku G. k.
pri dostizhenii v centre zvezdy plotnosti rs
~ 1013 g/sm3 i temp-ry Ts ~ 1011K. Posle ostanovki G.
k. nachinaetsya process obrazovaniya goryachei
neitronnoi zvezdy. Pri etom prodolzhaetsya
dovol'no medlennoe uvelichenie (vsya bystraya
stadiya G. k. do ostanovki harakterizuetsya
gidrodinamich. vremenem ~0,1 s) centr.
plotnosti do rs~1015 g/sm3 i temp-ry
Ts ~ 1012K (za
vremya »3s). Zatem proishodit eshe bolee
medlennyi process ohlazhdeniya goryachei
neitronnoi zvezdy, zavershayushiisya
obrazovaniem holodnoi neitronnoi zvezdy,
dlya k-roi massa ![]() eshe dopustima (sm.
Neitronnye
zvezdy).
eshe dopustima (sm.
Neitronnye
zvezdy).
Takoi zhe raschet (v ramkah toi zhe fiz.
modeli) G. k. massivnoi zvezdy, s ![]() (iz
nih massa zheleznogo yadra
(iz
nih massa zheleznogo yadra ![]() , ostal'noe
- kislorodnaya vnesh. obolochka), privodit k
inomu rezul'tatu. Ostanovki G. k. ne
poluchaetsya, i bystraya gidrodinamich. stadiya
G. k. prodolzhaetsya relyativistskim G. k., t. e.
zvezda prevrashaetsya v chernuyu dyru. Na ris. 2
naneseny traektorii centr. tochki zvezdy dlya
oboih obsuzhdaemyh raschetov G. k.:
, ostal'noe
- kislorodnaya vnesh. obolochka), privodit k
inomu rezul'tatu. Ostanovki G. k. ne
poluchaetsya, i bystraya gidrodinamich. stadiya
G. k. prodolzhaetsya relyativistskim G. k., t. e.
zvezda prevrashaetsya v chernuyu dyru. Na ris. 2
naneseny traektorii centr. tochki zvezdy dlya
oboih obsuzhdaemyh raschetov G. k.: ![]() (BB`) i
(BB`) i ![]() (AA`). Vidno, chto ostanovka G. k. v sluchae
BB` proishodit posle peresecheniya traektorii
centra zvezdy s pravoi (vneshnei) granicei
"ovraga neustoichivosti", gde
pokazatel' adiabaty g = 4/3.
V tochke ostanovki
pokazatel' g >> 4/3. V sluchae AA` traektoriya
prohodit (ris. 2) pravee traektorii VV`, i,
nesmotrya na to chto g > 4/3
posle peresecheniya
"ovraga neustoichivosti", G. k. dazhe ne
tormozitsya. T. o., pri nalichii moshnogo
neitrinnogo izlucheniya uvelichenie
uprugosti zvezdnogo veshestva eshe
nedostatochno dlya ostanovki G. k.
(AA`). Vidno, chto ostanovka G. k. v sluchae
BB` proishodit posle peresecheniya traektorii
centra zvezdy s pravoi (vneshnei) granicei
"ovraga neustoichivosti", gde
pokazatel' adiabaty g = 4/3.
V tochke ostanovki
pokazatel' g >> 4/3. V sluchae AA` traektoriya
prohodit (ris. 2) pravee traektorii VV`, i,
nesmotrya na to chto g > 4/3
posle peresecheniya
"ovraga neustoichivosti", G. k. dazhe ne
tormozitsya. T. o., pri nalichii moshnogo
neitrinnogo izlucheniya uvelichenie
uprugosti zvezdnogo veshestva eshe
nedostatochno dlya ostanovki G. k.
K fiz. prichinam, vyzyvayushim ostanovku G. k.
v sluchae ![]() , sleduet otnesti prezhde vsego
prekrashenie vseh processov vzaimnogo
prevrasheniya chastic, idushih s zatratoi
energii, i obrazovanie bol'shogo chisla
nuklonov iz yader gruppy zheleza i yader geliya.
Obrazovavshiisya nuklonnyi gaz (s izbytkom
chastichno vyrozhdennyh neitronov)
znachitel'no povyshaet uprugost' veshestva,
pri temn-re nedr Ts > 1010 K (znachenie
g dlya
takogo gaza priblizhaetsya k 5/3). Ne menee
vazhnym faktorom sleduet schitat'
voznikayushuyu na opredelennom etape szhatiya
neprozrachnost' tolshi zvezdy dlya
neitrinnogo izlucheniya. Neitrino i
antineitrino, besprepyatstvenno uhodivshie
do etogo iz zvezdy, v novyh usloviyah budut
pogloshat'sya veshestvom zvezdy. V rezul'tate
summarnye poteri energii u zvezdy
umen'shatsya, k tomu zhe odnovremenno
voznikayushii perenos energii neitrinnym
izlucheniem iz centra zvezdy v ee vnesh. sloi
mozhet neposredstvenno zatrudnit' G. k. vnesh.
sloev zvezdy. Mozhno schitat', chto
vozniknovenie neitrinnoi neprozrachnosti
na takoi stadii G. k., kogda vosstanovilas'
dostatochnaya uprugost' veshestva (g > 4/3),
sposobstvuet ostanovke G. k. Teoriya
neitrinnyh poter' energii, vklyuchaya voprosy
neprozrachnosti i perenosa energii
neitrinnym izlucheniem, yavl. odnoi iz
glavnyh zadach v issledovanii G. k. V
principe ostanovke G. k. mogut
sodeistvovat' takzhe vrashenie i magn. pole
zvezdy, no kolichestvenno eti vazhnye effekty
poka uchest' dovol'no trudno.
, sleduet otnesti prezhde vsego
prekrashenie vseh processov vzaimnogo
prevrasheniya chastic, idushih s zatratoi
energii, i obrazovanie bol'shogo chisla
nuklonov iz yader gruppy zheleza i yader geliya.
Obrazovavshiisya nuklonnyi gaz (s izbytkom
chastichno vyrozhdennyh neitronov)
znachitel'no povyshaet uprugost' veshestva,
pri temn-re nedr Ts > 1010 K (znachenie
g dlya
takogo gaza priblizhaetsya k 5/3). Ne menee
vazhnym faktorom sleduet schitat'
voznikayushuyu na opredelennom etape szhatiya
neprozrachnost' tolshi zvezdy dlya
neitrinnogo izlucheniya. Neitrino i
antineitrino, besprepyatstvenno uhodivshie
do etogo iz zvezdy, v novyh usloviyah budut
pogloshat'sya veshestvom zvezdy. V rezul'tate
summarnye poteri energii u zvezdy
umen'shatsya, k tomu zhe odnovremenno
voznikayushii perenos energii neitrinnym
izlucheniem iz centra zvezdy v ee vnesh. sloi
mozhet neposredstvenno zatrudnit' G. k. vnesh.
sloev zvezdy. Mozhno schitat', chto
vozniknovenie neitrinnoi neprozrachnosti
na takoi stadii G. k., kogda vosstanovilas'
dostatochnaya uprugost' veshestva (g > 4/3),
sposobstvuet ostanovke G. k. Teoriya
neitrinnyh poter' energii, vklyuchaya voprosy
neprozrachnosti i perenosa energii
neitrinnym izlucheniem, yavl. odnoi iz
glavnyh zadach v issledovanii G. k. V
principe ostanovke G. k. mogut
sodeistvovat' takzhe vrashenie i magn. pole
zvezdy, no kolichestvenno eti vazhnye effekty
poka uchest' dovol'no trudno.
K momentu ostanovki G. k. u zvezdy
obrazuetsya rezko vyrazhennaya geterogennaya
struktura: sil'no szhatoe yadro s massoi ![]() i
sravnitel'no malo szhavshayasya s nachala G. k.
obolochka, soderzhashaya ostal'nuyu massu
zvezdy. Kak pokazyvayut raschety, posle
ostanovki G. k. central'noi oblasti zvezdy
vnesh. sloi prodolzhayut padat' k centru i,
natolknuvshis' na plotnoe yadro, bystro
tormozyatsya. Tormozhenie padayushego, ili akkreciruyushego (sm.
Akkreciya),
veshestva osushestvlyaetsya v oblasti udarnogo
skachka na granice yadra i padayushei obolochki.
Pri dostatochno rezkoi ostanovke szhatiya
yadra etot skachok mozhet preobrazovat'sya v
moshnuyu udarnuyu volnu, rasprostranyayushuyusya
ot granicy yadra k periferii zvezdy. Na ris. 3,
postroennom na osnove odnogo iz raschetov G. k. s ochen' rezkoi ostanovkoi
dlya zvezdy s
i
sravnitel'no malo szhavshayasya s nachala G. k.
obolochka, soderzhashaya ostal'nuyu massu
zvezdy. Kak pokazyvayut raschety, posle
ostanovki G. k. central'noi oblasti zvezdy
vnesh. sloi prodolzhayut padat' k centru i,
natolknuvshis' na plotnoe yadro, bystro
tormozyatsya. Tormozhenie padayushego, ili akkreciruyushego (sm.
Akkreciya),
veshestva osushestvlyaetsya v oblasti udarnogo
skachka na granice yadra i padayushei obolochki.
Pri dostatochno rezkoi ostanovke szhatiya
yadra etot skachok mozhet preobrazovat'sya v
moshnuyu udarnuyu volnu, rasprostranyayushuyusya
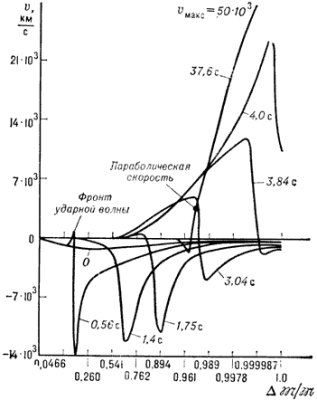
ot granicy yadra k periferii zvezdy. Na ris. 3,
postroennom na osnove odnogo iz raschetov G. k. s ochen' rezkoi ostanovkoi
dlya zvezdy s
![]() pokazano, kak po mere
rasprostraneniya udarnoi volny dvizhenie
veshestva k centru tormozitsya i smenyaetsya
razletom naruzhu. Pervonachal'no (ris. 3)
udarnaya volna sformirovalas' kak udarnyi
skachok pri
pokazano, kak po mere
rasprostraneniya udarnoi volny dvizhenie
veshestva k centru tormozitsya i smenyaetsya
razletom naruzhu. Pervonachal'no (ris. 3)
udarnaya volna sformirovalas' kak udarnyi
skachok pri ![]() v moment 0,56s. Ona
prodolzhaet sushestvovat' do momenta 1,75s v
vide udarnogo skachka, poka veshestvo za ee
frontom polnost'yu tormozitsya. V dal'neishem
proishodit rasprostranenie udarnoi volny. Ee skorost' vozrastaet s priblizheniem
fronta volny k poverhnosti zvezdy, t. k. ona
dvizhetsya iz plotnyh ko vse bolee
razrezhennym sloyam veshestva. Udarnaya volna
uskoryaetsya takzhe za schet detonacii
yadernogo goryuchego vo vnesh. sloyah zvezdy. Osn.
processom takogo roda, uchityvaemym v
raschete, yavl. prevrashenie yader 2168O
® 3216S
+ 16,54
MeV. V konce koncov udarnaya volna mozhet
vyzvat' otryv chasti obolochki ot zvezdy.
Primerno tak mogla by proishodit' vspyshka
sverhnovoi zvezdy.
v moment 0,56s. Ona
prodolzhaet sushestvovat' do momenta 1,75s v
vide udarnogo skachka, poka veshestvo za ee
frontom polnost'yu tormozitsya. V dal'neishem
proishodit rasprostranenie udarnoi volny. Ee skorost' vozrastaet s priblizheniem
fronta volny k poverhnosti zvezdy, t. k. ona
dvizhetsya iz plotnyh ko vse bolee
razrezhennym sloyam veshestva. Udarnaya volna
uskoryaetsya takzhe za schet detonacii
yadernogo goryuchego vo vnesh. sloyah zvezdy. Osn.
processom takogo roda, uchityvaemym v
raschete, yavl. prevrashenie yader 2168O
® 3216S
+ 16,54
MeV. V konce koncov udarnaya volna mozhet
vyzvat' otryv chasti obolochki ot zvezdy.
Primerno tak mogla by proishodit' vspyshka
sverhnovoi zvezdy.
 |
|
Ris. 3. Raspredelenie skorostei i dvizheniya
sloev zvezdy s maccoi |
No v bolee posledovatel'nyh raschetah G. k.
s ostanovkoi dostatochno moshnoi udarnoi
volny so skol'ko-nibud' znachitel'noi
kinetich. energiei razleta otorvavshihsya
sloev ne poluchaetsya. V raschete G. k. dlya
zvezdy s massoi ![]() (sluchai VV` na ris. 2)
voobshe ne poluchilos' nikakogo vybrosa vnesh.
sloev, dazhe s uchetom effekta vrasheniya.
Nablyudeniya zhe, naprotiv, svidetel'stvuyut o
tesnoi svyazi neitronnyh zvezd-pul'sarov i
vspyshek sverhnovyh. S etoi tochki zreniya
osobyi interes predstavlyayut issledovaniya G.
k. dlya zvezd malyh mass, priblizhayushihsya k t.
n. Chandrasekara predelu (
(sluchai VV` na ris. 2)
voobshe ne poluchilos' nikakogo vybrosa vnesh.
sloev, dazhe s uchetom effekta vrasheniya.
Nablyudeniya zhe, naprotiv, svidetel'stvuyut o
tesnoi svyazi neitronnyh zvezd-pul'sarov i
vspyshek sverhnovyh. S etoi tochki zreniya
osobyi interes predstavlyayut issledovaniya G.
k. dlya zvezd malyh mass, priblizhayushihsya k t.
n. Chandrasekara predelu (![]() dlya zheleznoi
zvezdy i
dlya zheleznoi
zvezdy i ![]() dlya uglerodnoi). Delo v tom,
chto v etih issledovaniyah byl obnaruzhen
ves'ma effektivnyi mehanizm vybrosa
obolochki zvezdy (sm. razdel 4). Na ris. 2
nanesena traektoriya SS`, izobrazhayushaya G. k.
dlya centra zvezdy s massoi
dlya uglerodnoi). Delo v tom,
chto v etih issledovaniyah byl obnaruzhen
ves'ma effektivnyi mehanizm vybrosa
obolochki zvezdy (sm. razdel 4). Na ris. 2
nanesena traektoriya SS`, izobrazhayushaya G. k.
dlya centra zvezdy s massoi ![]() k-ryi
soprovozhdaetsya vybrosom vnesh. sloev (kachestv.
storonu etogo effekta poyasnyaet ris. 3).
k-ryi
soprovozhdaetsya vybrosom vnesh. sloev (kachestv.
storonu etogo effekta poyasnyaet ris. 3).
4. Termoyadernyi vzryv uglerodno-kislorodnyh
zvezd (![]() ) i razvitie
gravitacionnogo kollapsa
) i razvitie
gravitacionnogo kollapsa
Vyshe uzhe govorilos', chto glavnym
mehanizmom, privodyashim k potere gidrostatich.
ustoichivosti malomassivnyh zvezd, yavl. beta-prevrasheniya,
a tochnee - zahvat elektronov yadrami i
protonami, t. e. neitronizaciya veshestva.
Yasno, chto process neitronizacii budet
sodeistvovat' G. k., poskol'ku pri zahvate
elektronov snizhaetsya elektronnoe davlenie,
a takzhe unositsya iz zvezdy v vide neitrino
opredelennaya energiya. Zametim, chto vnutri
malomassivnoi zvezdy davlenie vyrozhdennogo
gaza elektronov - osn. chast'
davleniya veshestva (sm. nachalo traektorii SS`
na ris. 2). G. k. malomassivnyh zvezd
otlichaetsya ot G. k. massivnyh zvezd eshe v
odnom otnoshenii. Posle "sgoraniya"
geliya i obrazovaniya uglerodno-kislorodnogo
yadra zvezdy (ris. 1) ee dal'neishaya evolyuciya
protekaet razlichno v zavisimosti ot massy
obrazovavshegosya yadra. G. k. massivnyh zvezd,
s ![]() , razvivaetsya (posle obrazovaniya
zheleznogo yadra zvezdy) tak, kak bylo opisano
na primere G. k. zvezd s
, razvivaetsya (posle obrazovaniya
zheleznogo yadra zvezdy) tak, kak bylo opisano
na primere G. k. zvezd s ![]() i s
i s ![]() . V
malomassivnyh zvezdah, s
. V
malomassivnyh zvezdah, s ![]() , G. k.
mozhet nachat'sya ran'she, pri vygoranii
ugleroda. Raschety pokazyvayut, chto eto
vygoranie protekaet, kak pravilo, burno, s
narusheniem gidrostatich. ravnovesiya zvezdy
i perehodit v termoyadernyi vzryv s bol'shim
vydeleniem energii.
, G. k.
mozhet nachat'sya ran'she, pri vygoranii
ugleroda. Raschety pokazyvayut, chto eto
vygoranie protekaet, kak pravilo, burno, s
narusheniem gidrostatich. ravnovesiya zvezdy
i perehodit v termoyadernyi vzryv s bol'shim
vydeleniem energii.
Odnako, nesmotrya na vzryvnoe gorenie
ugleroda i kisloroda, etot slozhnyi process
v konechnom schete mozhet privesti vse-taki k
razvitiyu G. k., a ne k vzryvu zvezdy. Etomu
sposobstvuyut intensivnaya neitronizaciya
produktov goreniya (yader gruppy zheleza) i
soprovozhdayushie ee znachit. poteri energii za
schet neitrinnogo izlucheniya. Intensivnost'
ukazannyh processov bystro rastet s
uvelicheniem plotnosti v centre zvezdy. Iz
raschetov sleduet, chto termoyadernyi vzryv
uglerodno-kislorodnoi zvezdy
deistvitel'no perehodit v G. k., esli centr.
plotnost' zvezdy do nachala vygoraniya
prevyshaet znachenie rs »1010 g/sm3.
Principial'naya vozmozhnost' G. k. takzhe
vytekaet iz sravneniya chandrasekarovskogo
predela dlya zheleznoi zvezdy (![]() ) n massy
rassmatrivaemoi uglerodno-kislorodnoi
zvezdy (
) n massy
rassmatrivaemoi uglerodno-kislorodnoi
zvezdy (![]() ). Prevyshenie massy poslednei
nad chandrasekarovskim predelom yavl.
neobhodimym usloviem G. k., a
). Prevyshenie massy poslednei
nad chandrasekarovskim predelom yavl.
neobhodimym usloviem G. k., a ![]() g/sm3 -
dostatochnym usloviem.
g/sm3 -
dostatochnym usloviem.
 |
|
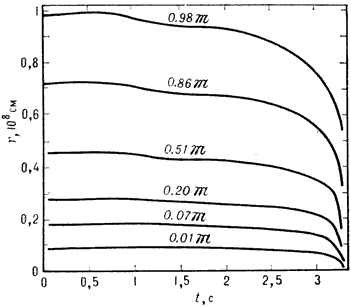
Ris. 4. Izmenenie so vremenem radiusov
sloev |
Prevrashenie termoyadernogo vzryva v G. k. illyustriruet ris. 4, gde izobrazheno izmenenie so vremenem radiusov nesk. sloev uglerodno-kislorodnoi zvezdy (traektoriya ee centr, tochki SS` dana na ris. 2). V moment vremeni t = 3,3 s (vremya otschityvaetsya ot momenta, kogda temp-pa v centre zvezdy dostigla znacheniya 6.108K, dostatochnogo dlya razvitiya vzryvnogo termoyadernogo goreniya ugleroda) radiusy vseh sloev rezko umen'shayutsya, chto i oznachaet perehod vzryva v G. k.
Razvivayushiisya G. k. soprovozhdaetsya vse
vozrastayushim potokom neitrinnogo izlucheniya, k-ryi, chastichno peredavaya svoyu
energiyu veshestvu vnesh. sloev zvezdy,
znachitel'no uskoryaet termoyadernoe gorenie
ostatkov ugleroda v etih sloyah. Formiruetsya
moshnaya detonac. volna s polozhit. skorostyami
veshestva pozadi fronta, dostatochnymi dlya
otryva naruzhnoi obolochki. Detal'nyi uchet
etogo mehanizma v raschetah i pokazyvaet, chto
razletayusheisya obolochke peredaetsya energiya
~1050 erg.
Zatem kinetich. energiya obolochki mozhet
uvelichit'sya (no uzhe v gorazdo bolee
medlennom tempe, za 105-106 s) za schet
effektov vrasheniya i davleniya magn. polya do
velichiny ~1031 erg, chto sootvetstvuet energii
obolochki tipichnoi sverhnovoi zvezdy. Esli v
uglerodno-kislorodnoi zvezde central'naya
plotnost' dokriticheskaya (![]() g/sm3), to
pri termoyadernom gorenii v nei mozhet ili
spokoino obrazovat'sya zheleznoe yadro v
rezul'tate vygoraniya chasti veshestva, ili
razvit'sya pul'sacionnyi rezhim
termoyadernogo goreniya ugleroda s
posleduyushim vzryvom zvezdy. Teoriya
evolyucii zvezd pokazyvaet, chto razlichie v
znacheniyah centr. plotnosti uglerodno-kislorodnyh
zvezd, opredelyayushee ih dal'neishuyu sud'bu,
mozhet byt' vyzvano usloviyami razvitiya
zvezd v sostave tesnyh dvoinyh sistem.
g/sm3), to
pri termoyadernom gorenii v nei mozhet ili
spokoino obrazovat'sya zheleznoe yadro v
rezul'tate vygoraniya chasti veshestva, ili
razvit'sya pul'sacionnyi rezhim
termoyadernogo goreniya ugleroda s
posleduyushim vzryvom zvezdy. Teoriya
evolyucii zvezd pokazyvaet, chto razlichie v
znacheniyah centr. plotnosti uglerodno-kislorodnyh
zvezd, opredelyayushee ih dal'neishuyu sud'bu,
mozhet byt' vyzvano usloviyami razvitiya
zvezd v sostave tesnyh dvoinyh sistem.
5. Vspyshki sverhnovyh zvezd, statistika kollapsiruyushih zvezd, vozmozhnosti nablyudenii
Teoriya G. k. privodit, sledovatel'no, k
vyvodu, chto so vspyshkami sverhnovyh svyazan
kollaps malomassivnyh uglerodno-kislorodnyh
zvezd, s massoi ok. ![]() . Dopolnit. analiz
pokazyvaet, chto G. k. s obrazovaniem goryachei
neitronnoi zvezdy i vybrosom (v dva etapa)
vnesh. obolochki mozhno otozhdestvit' so
sverhnovymi I tipa. V to zhe vremya vzryv
zvezdy bez obrazovaniya neitronnoi zvezdy
mozhno postavit' v sootvetstvie so
sverhnovymi II tipa. Sleduet vse zhe zametit',
chto takie otozhdestvleniya ne vpolne
odnoznachny i ne isklyuchayut dr. variantov.
Teoreticheski vozmozhen G. k. bez vspyshki
sverhnovoi, kak eto bylo ustanovleno v
raschetah G. k. massivnyh zheleznyh yader zvezd.
Pri etom processe G. k. mozhet zavershat'sya
rozhdeniem neitronnyh zvezd ili chernyh dyr.
. Dopolnit. analiz
pokazyvaet, chto G. k. s obrazovaniem goryachei
neitronnoi zvezdy i vybrosom (v dva etapa)
vnesh. obolochki mozhno otozhdestvit' so
sverhnovymi I tipa. V to zhe vremya vzryv
zvezdy bez obrazovaniya neitronnoi zvezdy
mozhno postavit' v sootvetstvie so
sverhnovymi II tipa. Sleduet vse zhe zametit',
chto takie otozhdestvleniya ne vpolne
odnoznachny i ne isklyuchayut dr. variantov.
Teoreticheski vozmozhen G. k. bez vspyshki
sverhnovoi, kak eto bylo ustanovleno v
raschetah G. k. massivnyh zheleznyh yader zvezd.
Pri etom processe G. k. mozhet zavershat'sya
rozhdeniem neitronnyh zvezd ili chernyh dyr.
K sozhaleniyu, poka trudno skazat' chto-libo
opredelennoe ob otnosit. chastote razlichnyh
ishodov evolyucii zvezd, i v chastnosti o
chastote G. k. Sushestvuyushaya statistika zvezd
utverzhdaet, chto chislo zvezd s ![]() ,
okanchivayushih svoyu yadernuyu evolyuciyu, rastet
s umen'sheniem
,
okanchivayushih svoyu yadernuyu evolyuciyu, rastet
s umen'sheniem ![]() kak
kak ![]() . V Galaktike,
soglasno etoi statistike, dlya
. V Galaktike,
soglasno etoi statistike, dlya ![]() chislo "umirayushih" zvezd za god
sostavlyaet »1. No statistika ne uchityvaet
processov poteri massy zvezdami v hode
evolyucii, a takzhe ryad dr. vazhnyh effektov,
ona, veroyatnee vsego, preuvelichivaet
chastotu G. k. V to zhe vremya vyvod o
preobladayushem vklade zvezd malyh mass v
chislo zvezd, zavershayushih evolyuciyu gravitac.
kollapsom, kazhetsya pravdopodobnym. Krome
togo, sleduet podcherknut', chto massa zvezdy,
o k-roi idet rech' v teorii pozdnih stadii
evolyucii, na samom dele predstavlyaet soboi
massu uglerodno-kislorodnogo yadra zvezdy,
imeyushei geterogennuyu strukturu giganta s
plotnym yadrom i razrezhennoi obolochkoi. Iz
raschetov evolyucii zvezd izvestno, chto massa
yadra v nesk. raz men'she massy vsei zvezdy (napr.,
massa yadra, ravnaya
chislo "umirayushih" zvezd za god
sostavlyaet »1. No statistika ne uchityvaet
processov poteri massy zvezdami v hode
evolyucii, a takzhe ryad dr. vazhnyh effektov,
ona, veroyatnee vsego, preuvelichivaet
chastotu G. k. V to zhe vremya vyvod o
preobladayushem vklade zvezd malyh mass v
chislo zvezd, zavershayushih evolyuciyu gravitac.
kollapsom, kazhetsya pravdopodobnym. Krome
togo, sleduet podcherknut', chto massa zvezdy,
o k-roi idet rech' v teorii pozdnih stadii
evolyucii, na samom dele predstavlyaet soboi
massu uglerodno-kislorodnogo yadra zvezdy,
imeyushei geterogennuyu strukturu giganta s
plotnym yadrom i razrezhennoi obolochkoi. Iz
raschetov evolyucii zvezd izvestno, chto massa
yadra v nesk. raz men'she massy vsei zvezdy (napr.,
massa yadra, ravnaya ![]() , sootvetstvuet
polnoi masse zvezdy
, sootvetstvuet
polnoi masse zvezdy ![]() ). Poka trudno
ukazat' znachenie naimen'shei massy
kollapsiruyushih zvezd, no ono, ochevidno,
dolzhno prevyshat' chandrasekarovskii predel
zheleznoi zvezdy (
). Poka trudno
ukazat' znachenie naimen'shei massy
kollapsiruyushih zvezd, no ono, ochevidno,
dolzhno prevyshat' chandrasekarovskii predel
zheleznoi zvezdy (![]() ).
).
Esli massa goryachei neitronnoi zvezdy
![]() takaya neitronnaya zvezda posle
korotkogo perioda intensivnogo
neitrinnogo ohlazhdeniya (nesk. desyatkov
sekund) ne dolzhna ispytyvat'
relyativistskoi G. k. i mozhet nablyudat'sya v
vide istochnika postepenno oslabevayushego
teplovogo rentg. izlucheniya, a takzhe dolgoe
vremya v vide pul'sara s izlucheniem v
diapazone ot radiovoln do gamma-luchei.
takaya neitronnaya zvezda posle
korotkogo perioda intensivnogo
neitrinnogo ohlazhdeniya (nesk. desyatkov
sekund) ne dolzhna ispytyvat'
relyativistskoi G. k. i mozhet nablyudat'sya v
vide istochnika postepenno oslabevayushego
teplovogo rentg. izlucheniya, a takzhe dolgoe
vremya v vide pul'sara s izlucheniem v
diapazone ot radiovoln do gamma-luchei.
V teorii G. k. osobenno interesen vopros o
neitrinnom izluchenii. V hode G. k.
izluchayutsya v vide impul'sa
prodolzhitel'nost'yu 10-30 s neitrino v i
antineitrino ![]() s polnoi energiei »3.1053 erg. V
pervom priblizhenii mozhno schitat', chto v i
s polnoi energiei »3.1053 erg. V
pervom priblizhenii mozhno schitat', chto v i
![]() v
etom impul'se predstavleny v primerno
ravnyh kolichestvah, prichem energiya
otdel'noi chasticy v srednem sostavlyaet 10-15
MeV. Raschetnaya krivaya neitrinnoi
svetimosti
v
etom impul'se predstavleny v primerno
ravnyh kolichestvah, prichem energiya
otdel'noi chasticy v srednem sostavlyaet 10-15
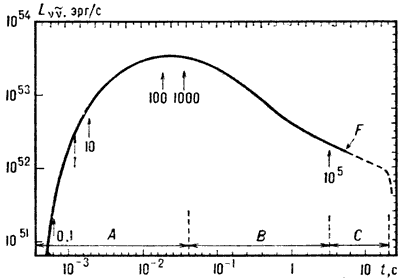
MeV. Raschetnaya krivaya neitrinnoi
svetimosti ![]() zvezdy s massoi
zvezdy s massoi ![]() izobrazhena na ris. 5. Nachalo otscheta vremeni
vybrano proizvol'no, kogda sr. opticheskaya
tolsha zvezdy
izobrazhena na ris. 5. Nachalo otscheta vremeni
vybrano proizvol'no, kogda sr. opticheskaya
tolsha zvezdy ![]() . Znacheniya optich. tolshi
. Znacheniya optich. tolshi
![]() ukazany okolo vertikal'nyh strelok. Osn.
chast' krivoi neitrinnoi svetimosti
sootvetstvuet usloviyam neitrinnoi
neprozrachnosti yadra zvezdy (
ukazany okolo vertikal'nyh strelok. Osn.
chast' krivoi neitrinnoi svetimosti
sootvetstvuet usloviyam neitrinnoi
neprozrachnosti yadra zvezdy (![]() ). Tochka F
ukazyvaet moment prekrasheniya gidrodinamich.
rascheta G. k. Bukvami A, V i S oboznacheny
razlichnye fazy G. k., k-rye harakterizuyutsya
sleduyushimi dannymi:
). Tochka F
ukazyvaet moment prekrasheniya gidrodinamich.
rascheta G. k. Bukvami A, V i S oboznacheny
razlichnye fazy G. k., k-rye harakterizuyutsya
sleduyushimi dannymi:
| A | B | C | |
| 1 | 17 | 30 | |
| 12 | 14 | 15 | |
| Dt, c | 0,04 | 3,1 | 15 |
Zdes' ![]() - polnaya energiya vseh sortov
neitrino, vklyuchaya elektronnye i myuonnye;
- polnaya energiya vseh sortov
neitrino, vklyuchaya elektronnye i myuonnye; ![]() - sr. energiya neitrino i antineitrino; Dt
- prodolzhitel'nost' sootvetstvuyushei fazy G.
k.
- sr. energiya neitrino i antineitrino; Dt
- prodolzhitel'nost' sootvetstvuyushei fazy G.
k.
 |
|
Ris. 5. Izmenenie neitrinnoi svetimosti |
Znachit. dlitel'nost' neitrinnogo svecheniya ob'yasnyaetsya tem, chto osn. dolya energii izluchaetsya ne v processe bystroi gidrodinamich. stadii G. k., a na posleduyushei stadii akkrecii veshestva vnesh. sloev (faza V, ris. 5) i ohlazhdeniya goryachei gidrostaticheski ravnovesnoi neitronnoi zvezdy (faza S). Neitrinnyi impul's, izluchennyi kollapsiruyushei v predelah nashei Galaktiki zvezdoi, v principe mozhet byt' zaregistrirovan na imeyushihsya uzhe detektorah neitrinnogo izlucheniya (sm. Neitrinnaya astronomiya). Obnaruzhenie neitrinnogo impul'sa stalo by neposredstvennoi nablyudatel'noi proverkoi teorii G. k. V chastnosti, ono pozvolilo by proverit' vazhnyi vyvod teorii o vozmozhnosti G. k., protekayushego bez sbrosa obolochki i, sledovatel'no, bez nablyudaemyh effektov tipa vspyshek sverhnovyh. Takih processov v Galaktike mozhet proishodit', kak uzhe govorilos', »1 v god.
V processe G. k. zvezdnyh yader s massoi, ne
prevyshayushei massu holodnoi neitronnoi
zvezdy (![]() ), effekty obshei teorii
otnositel'nosti (OTO) ne ochen' sushestvenny,
hotya ih nuzhno budet uchityvat' pri
posleduyushem razvitii teorii G. k. Odnako
effekty OTO imeyut reshayushee znachenie dlya
relyativistskogo G. k., k-rym zakanchivaetsya
evolyuciya massivnyh zvezdnyh yader.
), effekty obshei teorii
otnositel'nosti (OTO) ne ochen' sushestvenny,
hotya ih nuzhno budet uchityvat' pri
posleduyushem razvitii teorii G. k. Odnako
effekty OTO imeyut reshayushee znachenie dlya
relyativistskogo G. k., k-rym zakanchivaetsya
evolyuciya massivnyh zvezdnyh yader.
Lit.: Zel'dovich Ya. B., Novikov P. D., Teoriya tyagoteniya i evolyuciya zvezd, M., 1971; Shklovskii I. S., Sverhnovye zvezdy i svyazannye s nimi problemy, 2 izd., M., 1976, s. 398 i posl.; Na perednem krae astrofiziki, per. s angl., M., 1979; Imshennik V. S., Nadezhin D. K., Konechnye stadii evolyucii zvezd i vspyshki sverhnovyh, v kn.: Itogi nauki n tehniki. Ser. Astronomiya, t. 21, M., 1982.
(V.S. Imshennik)
V. S. Imshennik, "Fizika Kosmosa", 1986
Glossarii Astronet.ru
|
Publikacii s klyuchevymi slovami:
gravitacionnyi kollaps
Publikacii so slovami: gravitacionnyi kollaps | |
|
Sm. takzhe:
| |