Kakuyu formu imeet nasha Vselennaya?

^{(stat'ya opublikovana v zhurnale "}Nauka i Zhizn'", N8, 2002 g.)

V drevnosti lyudi polagali, chto zhivut na obshirnoi ploskoi poverhnosti, hotya i pokrytoi koe-gde gorami i vpadinami. Eto ubezhdenie sohranyalos' na protyazhenii mnogih tysyach let, poka Aristotel' v IV veke do n. e. ne zametil, chto uhodyashee v more sudno propadaet iz vidu ne potomu, chto po mere udaleniya umen'shaetsya do nedostupnyh glazu razmerov. Naprotiv, snachala ischezaet korpus korablya, potom parusa i, nakonec, machty. Eto privelo ego k zaklyucheniyu, chto Zemlya dolzhna byt' krugloi.

Chto obshego mezhdu listom bumagi, poverhnost'yu stola, bublikom i kruzhkoi? Konechno, mozhno, sidya za stolom, s'est' bublik, lezhashii na bumazhke, i zapit' molokom iz kruzhki. No mezhdu nimi imeetsya i bolee tesnaya svyaz': s tochki zreniya geometrii ih poverhnosti absolyutno odinakovy.

Za proshedshie tysyacheletiya sdelano mnozhestvo otkrytii, nakoplen kolossal'nyi opyt. I tem ne menee do sih por ostayutsya bez otveta fundamental'nye voprosy: konechna ili beskonechna Vselennaya, vnutri kotoroi my obitaem, i kakova ee forma?

Poslednie nablyudeniya astronomov i issledovaniya matematikov pokazyvayut, chto formu nashei Vselennoi sleduet iskat' sredi vosemnadcati tak nazyvaemyh trehmernyh orientiruemyh evklidovyh mnogoobrazii, prichem pretendovat' na nee mogut tol'ko desyat'.

Nablyudaemaya Vselennaya

Lyubye umozaklyucheniya o vozmozhnoi forme nashei Vselennoi dolzhny opirat'sya na real'nye fakty, poluchennye iz astronomicheskih nablyudenii. Bez etogo dazhe samye krasivye i pravdopodobnye gipotezy obrecheny na neudachu. Poetomu posmotrim, chto govoryat o Vselennoi rezul'taty nablyudenii.

Prezhde vsego, zametim, chto, v kakom by meste Vselennoi my ni nahodilis', vokrug lyuboi ee tochki mozhno ochertit' sferu proizvol'nogo razmera, soderzhashuyu vnutri prostranstvo Vselennoi. Takoe neskol'ko iskusstvennoe postroenie govorit kosmologam, chto prostranstvo Vselennoi predstavlyaet soboi trehmernoe mnogoobrazie (3-mnogoobrazie).

Srazu zhe voznikaet vopros: a kakoe imenno mnogoobrazie predstavlyaet nashu Vselennuyu? Matematiki davno ustanovili, chto ih tak mnogo, chto polnogo spiska do sih por ne sushestvuet. Mnogoletnie nablyudeniya pokazali, chto Vselennaya obladaet ryadom fizicheskih svoistv, kotorye rezko sokrashayut chislo vozmozhnyh pretendentov na ee formu. I odno iz glavnyh takih svoistv topologii Vselennoi - ee krivizna.

Soglasno prinyatoi na segodnyashnii den' koncepcii, primerno cherez 300 tysyach let posle Bol'shogo vzryva temperatura Vselennoi upala do urovnya, dostatochnogo dlya ob'edineniya elektronov i protonov v pervye atomy. Kogda eto proizoshlo, izluchenie, kotoroe vnachale rasseivalos' zaryazhennymi chasticami, vnezapno poluchilo vozmozhnost' besprepyatstvenno prohodit' cherez rasshiryayushuyusya Vselennuyu. Eto izvestnoe nyne kak kosmicheskoe mikrovolnovoe fonovoe, ili reliktovoe, izluchenie udivitel'no odnorodno i obnaruzhivaet tol'ko ochen' slabye otkloneniya (fluktuacii) intensivnosti ot srednego znacheniya. Takaya odnorodnost' mozhet byt' tol'ko vo Vselennoi, krivizna kotoroi vsyudu postoyanna.

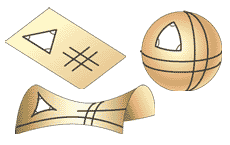Dvuhmernye analogi evklidovoi, sfericheskoi i giperbolicheskoi geometrii. V ploskom evklidovom prostranstve parallel'nye pryamye nigde ne peresekayutsya, a summa uglov lyubogo treugol'nika ravna 180 gradusam. Na sfericheskoi poverhnosti chast' parallel'nyh pryamyh peresekaetsya, podobno meridianam na zemnom globuse, a summa uglov treugol'nikov vsegda bol'she 180 gradusov (vplot' do 360). Na poverhnosti giperboloida ugly treugol'nikov sostavlyayut men'she 180 gradusov, a parallel'nye pryamye mogut rashodit'sya, nigde ne peresekayas'.

Postoyanstvo krivizny oznachaet, chto prostranstvo Vselennoi imeet odnu iz treh vozmozhnyh geometrii: ploskuyu evklidovu sfericheskuyu s polozhitel'noi kriviznoi ili giperbolicheskuyu s otricatel'noi. Eti geometrii obladayut sovershenno raznymi svoistvami. Tak, naprimer, v evklidovoi geometrii summa uglov treugol'nika ravna tochno 180 gradusam. V sfericheskoi i giperbolicheskoi geometriyah eto ne tak. Esli na sfere vzyat' tri tochki i provesti mezhdu nimi pryamye, to summa uglov mezhdu nimi sostavit bol'she 180 gradusov (vplot' do 360). V giperbolicheskoi zhe geometrii eta summa men'she 180 gradusov. Imeyutsya i drugie kardinal'nye otlichiya.

Tak kakuyu zhe geometriyu dlya nashei Vselennoi vybrat': evklidovu, sfericheskuyu ili giperbolicheskuyu?

Nemeckii matematik Karl Fridrih Gauss eshe v pervoi polovine XIX stoletiya ponimal, chto real'noe prostranstvo okruzhayushego mira mozhet byt' i neevklidovym. Provodya mnogoletnie geodezicheskie raboty v Gannoverskom korolevstve, Gauss zadalsya cel'yu s pomosh'yu pryamyh izmerenii issledovat' geometricheskie svoistva fizicheskogo prostranstva. Dlya etogo on vybral tri udalennye odna ot drugoi gornye vershiny - Hohengagen, Inzel'berg i Brokken. Stoya na odnoi iz etih vershin, on napravlyal otrazhennye zerkalami solnechnye luchi na dve drugie i izmeryal ugly mezhdu storonami ogromnogo svetovogo treugol'nika. Tem samym on pytalsya otvetit' na vopros: iskrivlyayutsya li traektorii svetovyh luchei, prohodyashih nad sfericheskim prostranstvom Zemli? (Kstati, primerno v eto zhe vremya rossiiskii matematik, rektor Kazanskogo universiteta Nikolai Ivanovich Lobachevskii predlozhil eksperimental'no issledovat' vopros o geometrii fizicheskogo prostranstva, ispol'zuya zvezdnyi treugol'nik.) Esli by Gauss obnaruzhil, chto summa uglov svetovogo treugol'nika otlichaetsya ot 180 gradusov, to posledoval by vyvod, chto storony treugol'nika iskrivleny i real'noe fizicheskoe prostranstvo neevklidovo. Odnako v predelah oshibki izmerenii summa uglov "proverochnogo treugol'nika Brokken - Hohengagen - Inzel'berg" sostavlyala rovno 180 gradusov.

Itak, v malyh (po astronomicheskim merkam) masshtabah Vselennaya predstaet kak evklidova (hotya, konechno, ekstrapolirovat' vyvody Gaussa na vsyu Vselennuyu nel'zya).

Nedavnie issledovaniya, provedennye s pomosh'yu vysotnyh aerostatov, podnyatyh nad Antarktidoi, takzhe podtverzhdayut etot vyvod. Pri izmerenii uglovogo spektra moshnosti reliktovogo izlucheniya byl zaregistrirovan pik, kotoryi, kak polagayut issledovateli, mozhet byt' ob'yasnen tol'ko sushestvovaniem holodnoi chernoi materii - otnositel'no bol'shih, medlenno dvizhushihsya ob'ektov - imenno v evklidovoi Vselennoi. Drugie issledovaniya takzhe podtverzhdayut etot vyvod, chto rezko sokrashaet kolichestvo veroyatnyh pretendentov na vozmozhnuyu formu Vselennoi.

Eshe v tridcatyh godah XX stoletiya matematiki dokazali, chto sushestvuet tol'ko 18 razlichnyh evklidovyh trehmernyh mnogoobrazii i, sledovatel'no, tol'ko 18 vozmozhnyh form Vselennoi vmesto ih beskonechnogo chisla. Ponimanie svoistv etih mnogoobrazii pomogaet eksperimental'no opredelit' istinnuyu formu Vselennoi, tak kak celenapravlennyi poisk vsegda effektivnee poiska vslepuyu.

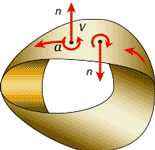List Mebiusa s tochkoi a na ego poverhnosti, normal'yu k nei i malen'koi okruzhnost'yu s zadannym napravleniem v. Polnyi obhod vokrug lista izmenyaet napravlenie okruzhnosti na protivopolozhnoe. Eto govorit o tom, chto poverhnost' lista Mebiusa neorientiruema.

Odnako chislo vozmozhnyh form Vselennoi mozhno sokratit' eshe. Deistvitel'no, sredi 18 evklidovyh 3-mnogoobrazii imeetsya 10 orientiruemyh i 8 neorientiruemyh. Poyasnim, chto predstavlyaet soboi ponyatie orientiruemosti. Dlya etogo rassmotrim interesnuyu dvuhmernuyu poverhnost' - list Mebiusa. Ego mozhno poluchit' iz pryamougol'noi poloski bumagi, perekruchennoi odin raz i skleennoi koncami. Teper' voz'mem na liste Mebiusa tochku , provedem k nei normal' (perpendikulyar), a vokrug normali nachertim nebol'shuyu okruzhnost' s napravleniem protiv chasovoi strelki, esli smotret' iz konca normali. Nachnem peremeshat' tochku vmeste s normal'yu i napravlennoi okruzhnost'yu po listu Mebiusa. Kogda tochka oboidet ves' list i vernetsya v ishodnoe polozhenie (zritel'no ona budet na drugoi storone lista, no v geometrii poverhnost' tolshiny ne imeet), napravlenie normali izmenitsya na obratnoe, a napravlenie okruzhnosti - na protivopolozhnoe. Takie traektorii nazyvayutsya putyami, obrashayushimi orientaciyu. A poverhnosti, imeyushie ih, nazyvayut neorientiruemymi ili odnostoronnimi. Poverhnosti zhe, na kotoryh ne sushestvuet obrashayushih orientaciyu zamknutyh putei, naprimer sfera, tor i neperekruchennaya lenta, nazyvayut orientiruemymi ili dvuhstoronnimi. Zametim kstati, chto list Mebiusa predstavlyaet soboi evklidovo neorientiruemoe dvuhmernoe mnogoobrazie.

Esli dopustit', chto nasha Vselennaya - neorientiruemoe mnogoobrazie, to fizicheski eto oznachalo by sleduyushee. Esli my poletim s Zemli vdol' zamknutoi petli, obrashayushei orientaciyu, to, konechno, vernemsya domoi, no okazhemsya v zerkal'noi kopii Zemli. My ne zametim v sebe nikakih izmenenii, no po otnosheniyu k nam u ostal'nyh zhitelei Zemli serdce okazhetsya sprava, vse chasy poidut protiv chasovoi strelki, a teksty predstanut v zerkal'nom otobrazhenii.

Maloveroyatno, chto my zhivem v takom mire. Kosmologi polagayut, chto esli by nasha Vselennaya byla neorientiruemoi, to proishodilo by izluchenie energii iz pogranichnyh zon, v kotoryh vzaimodeistvuyut materiya i antimateriya. Odnako nichego podobnogo nikogda ne nablyudalos', hotya teoreticheski i mozhno predpolozhit', chto podobnye zony sushestvuyut za predelami oblasti Vselennoi, dostupnoi nashemu vzglyadu. Poetomu rezonno isklyuchit' iz rassmotreniya vosem' neorientiruemyh mnogoobrazii i ogranichit' vozmozhnye formy nashei Vselennoi desyat'yu orientiruemymi evklidovymi trehmernymi mnogoobraziyami.

Vozmozhnye formy Vselennoi

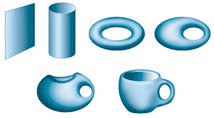Ploskii list bumagi mozhno skleit' v cilindr i, soediniv ego torcy, poluchit' tor. Pri deformacii poverhnosti tora poluchaetsya "chashka s ruchkoi". Manipulyacii osushestvlyalis' bez razrezov i skladok, poetomu vse eti tela imeyut odinakovuyu topologiyu, oni gomeomorfny. Na ih poverhnosti deistvuyut zakony evklidovoi geometrii.

Tor s odnoi ruchkoi gomeomorfen sfere s dvumya ruchkami - ih topologiya odinakova.

Trehmernye mnogoobraziya v chetyrehmernom prostranstve neobychaino trudny dlya naglyadnogo predstavleniya. Odnako mozhno popytat'sya predstavit' sebe ih strukturu, esli primenit' podhod, ispol'zuemyi v topologii dlya vizualizacii dvuhmernyh mnogoobrazii (2-mnogoobrazii) v nashem trehmernom prostranstve. Vse ob'ekty v nem schitayutsya kak by sdelannymi iz kakogo-to prochnogo elastichnogo materiala vrode reziny, dopuskayushego lyubye rastyazheniya i iskrivleniya, no bez razryvov, skladok i skleek. V topologii figury, kotorye mozhno s pomosh'yu takih deformacii preobrazovyvat' odnu v druguyu, nazyvayut gomeomorfnymi; oni imeyut odinakovuyu vnutrennyuyu geometriyu. Poetomu s tochki zreniya topologii bublik (tor) i obychnaya chashka s ruchkoi - odno i to zhe. A vot futbol'nyi myach perevesti v bublik nevozmozhno. Eti poverhnosti topologicheski razlichny, to est' imeyut razlichnye vnutrennie geometricheskie svoistva. Odnako esli na sfere vyrezat' krugluyu dyrku i pridelat' k nei odnu ruchku, to poluchivshayasya figura uzhe budet gomeomorfna toru.

Sushestvuet mnozhestvo poverhnostei, kotorye topologicheski otlichny ot tora i sfery. Naprimer, dobaviv k toru ruchku, podobnuyu toi, chto my vidim u chashki, my poluchim novuyu dyrku, a znachit, i novuyu figuru. Tor s ruchkoi budet gomeomorfen figure, napominayushei krendel', kotoraya v svoyu ochered' gomeomorfna sfere s dvumya ruchkami. Dobavlenie kazhdoi novoi ruchki sozdaet eshe odnu dyrku, a znachit, i druguyu poverhnost'. Takim sposobom mozhno poluchat' beskonechnoe ih kolichestvo.

Vse takie poverhnosti nazyvayutsya dvuhmernymi mnogoobraziyami ili prosto 2-mnogoobraziyami. Eto oznachaet, chto vokrug lyuboi ih tochki mozhno ochertit' okruzhnost' proizvol'nogo radiusa. Na poverhnosti Zemli mozhno narisovat' krug, soderzhashii ee tochki. Esli my vidim tol'ko takuyu kartinu, rezonno schitat', chto ona predstavlyaet soboi beskonechnuyu ploskost', sferu, tor ili voobshe lyubuyu druguyu poverhnost' iz beskonechnogo chisla torov ili sfer s razlichnym chislom ruchek.

Eti topologicheskie formy mogut byt' dovol'no slozhny dlya ponimaniya. I chtoby legche i otchetlivee predstavi t' ih sebe, skleim cilindr iz kvadratnogo lista bumagi, soediniv ego levuyu i pravuyu storony. Kvadrat v etom sluchae nazyvaetsya fundamental'noi oblast'yu dlya tora. Esli teper' myslenno skleit' osnovaniya cilindra (material cilindra elastichen), poluchitsya tor.

Predstavim sebe, chto est' nekoe dvuhmernoe sushestvo, skazhem nasekomoe, dvizhenie kotorogo po poverhnosti tora nuzhno issledovat'. Sdelat' eto neprosto, i gorazdo udobnee nablyudat' ego dvizhenie po kvadratu - prostranstvu s toi zhe topologiei. Etot priem imeet dva preimushestva. Vo-pervyh, pozvolyaet naglyadno uvidet' put' nasekomogo v trehmernom prostranstve, sledya za ego peremesheniem v dvuhmernom prostranstve, a vo-vtoryh, pozvolyaet ostavat'sya v ramkah horosho razvitoi evklidovoi geometrii na ploskosti. V evklidovoi geometrii soderzhitsya postulat o parallel'nyh pryamyh: dlya lyuboi pryamoi linii i tochki vne ee sushestvuet edinstvennaya pryamaya, parallel'naya pervoi i prohodyashaya cherez etu tochku. Krome togo, summa uglov ploskogo treugol'nika v tochnosti ravna 180 gradusam. No poskol'ku kvadrat opisyvaetsya evklidovoi geometriei, my mozhem rasprostranit' ee na tor i utverzhdat', chto tor - evklidovo 2-mnogoobrazie.

Nerazlichimost' vnutrennih geometrii dlya samyh raznyh poverhnostei svyazana s vazhnoi ih topologicheskoi harakteristikoi, nazyvaemoi razvertyvaemost'yu. Tak, poverhnosti cilindra i konusa vyglyadyat sovershenno razlichnymi, no tem ne menee ih geometrii absolyutno odinakovy. Obe oni mogut byt' razvernuty v ploskosti bez izmeneniya dlin otrezkov i uglov mezhdu nimi, poetomu dlya nih spravedliva evklidova geometriya. Eto zhe otnositsya i k toru, poskol'ku on predstavlyaet soboi poverhnost', razvertyvayushuyusya v kvadrat. Takie poverhnosti nazyvayut izometrichnymi.

Beschislennoe chislo torov mozhno sformirovat' i iz drugih ploskih figur, naprimer iz razlichnyh parallelogrammov ili shestiugol'nikov, skleivaya ih protivopolozhnye kraya. Odnako dlya etogo goditsya daleko ne kazhdyi chetyrehugol'nik: dliny ego skleennyh storon dolzhny byt' odinakovy mi. Takoe trebovanie neobhodimo, chtoby izbezhat' pri skleike udlinenii ili szhimanii kraev oblasti, kotorye narushayut evklidovu geometriyu poverhnosti.

Teper' pereidem k mnogoobraziyam bol'shei razmernosti.

Predstavlenie vozmozhnyh form Vselennoi

Poprobuem predstavit' sebe vozmozhnye formy nashei Vselennoi, kotorye, kak my uzhe videli, nado iskat' sredi desyati orientiruemyh evklidovyh trehmernyh mnogoobrazii.

Dlya predstavleniya evklidova 3-mnogoobraziya primenim ispol'zovannyi vyshe metod dlya dvuhmernyh mnogoobrazii. Tam my ispol'zovali v kachestve fundamental'noi oblasti tora kvadrat, a dlya predstavleniya trehmernogo mnogoobraziya stanem brat' trehmernye ob'ekty.

Voz'mem vmesto kvadrata kub i podobno tomu, kak my skleivali protivopolozhnye kraya kvadrata, skleim vmeste protivopolozhnye grani kuba vo vseh ih tochkah.

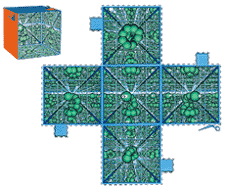Esli vyrezat' etu figuru i skleit' iz nee kub, stanet ponyatno, kak vyglyadit trehmernyi tor, beskonechno povtoryayushii kopii zelenogo "chervyachka", sidyashego v ego centre.

Poluchivshiisya trehmernyi tor predstavlyaet soboi evklidovo 3-mnogoobrazie. Esli my kakim-to obrazom okazalis' by v nem i posmotreli vpered, to uvideli by svoi zatylok, a takzhe svoi kopii v kazhdoi grani kuba - vperedi, szadi, sleva, sprava, vverhu i vnizu. Za nimi my by uvidali beskonechnoe mnozhestvo drugih kopii, podobno tomu, kak esli by okazalis' v komnate, gde steny, pol i potolok pokryty zerkalami. No izobrazheniya v trehmernom tore budut pryamymi, a ne zerkal'nymi.

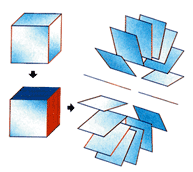Kub - fundamental'naya oblast' trehmernogo tora - razrezan na tonkie vertikal'nye sloi, kotorye pri skleivanii obrazuyut kol'co, sostoyashee iz dvuhmernyh torov.

Vazhno otmetit' krugovuyu prirodu etogo i mnogih drugih mnogoobrazii. Esli by Vselennaya deistvitel'no imela takuyu formu, to, pokinuv Zemlyu i letya bez kakih-libo izmenenii kursa, my v konce koncov vernulis' by domoi. Nechto podobnoe nablyudaetsya i na Zemle: dvigayas' na zapad vdol' ekvatora, my rano ili pozdno vernemsya v ishodnuyu tochku s vostoka.

Razrezav kub na tonkie vertikal'nye sloi, my poluchim nabor kvadratov. Protivopolozhnye kraya etih kvadratov dolzhny byt' skleeny vmeste, potomu chto oni sostavlyayut protivopolozhnye grani kuba. Tak chto trehmernyi tor okazyvaetsya kol'com, sostoyashim iz dvuhmernyh torov. Vspomnim, chto perednii i zadnii kvadraty takzhe skleeny i sluzhat granyami kuba. Topologi oboznachayut takoe mnogoobrazie kak T²xS¹, gde T² oznachaet dvuhmernyi tor, a S¹ - kol'co. Eto primer svyazki, ili puchka, torov.

Trehmernye tory mogut byt' polucheny ne tol'ko s pomosh'yu kuba. Podobno tomu kak parallelogramm obrazuet 2-tor, skleivaya protivopolozhnye grani parallelepipeda (trehmernogo tela, ogranichennogo parallelogrammami), my sozdadim 3-tor. Iz raznyh parallelepipedov obrazuyutsya prostranstva s razlichnymi zamknutymi putyami i uglami mezhdu nimi.

Trehmernyi tor mozhno skleit' iz kuba, podobno tomu, kak tor dvuhmernyi - iz kvadrata. Raznocvetnye "chervyachki", puteshestvuyushie vnutri ego, naglyadno demonstriruyut, kakie grani kuba skleeny vmeste.

Eti i vse drugie konechnye mnogoobraziya ochen' prosto vklyuchayutsya v kartinu rasshiryayusheisya Vselennoi. Esli fundamental'naya oblast' mnogoobraziya postoyanno rasshiryaetsya, obrazovannoe eyu prostranstvo budet rasshiryat'sya tozhe. Kazhdaya tochka v rasshiryayushemsya prostranstve vse dal'she otdalyaetsya ot ostal'nyh, chto v tochnosti sootvetstvuet kosmologicheskoi modeli. Pri etom, odnako, nuzhno prinyat' vo vnimanie, chto tochki vblizi odnoi grani vsegda budut sosedstvovat' s tochkami na protivopolozhnoi grani, poskol'ku, vne zavisimosti ot razmera fundamental'noi oblasti, protivopolozhnye grani skleeny.

Sleduyushee trehmernoe mnogoobrazie, pohozhee na trehmernyi tor, nazyvaetsya 1/2-povernutoe kubicheskoe prostranstvo. V etom prostranstve fundamental'noi oblast'yu snova sluzhit kub ili parallelepiped. Chetyre grani skleeny kak obychno, a ostavshiesya dve, perednyaya i zadnyaya, skleeny s povorotom na 180 gradusov: verhnyaya chast' perednei grani prikleena k nizhnei chasti zadnei. Esli by my okazalis' v takom mnogoobrazii i posmotreli na odnu iz etih granei, to uvideli by sobstvennuyu kopiyu, no perevernutuyu vverh nogami, za nei obychnuyu kopiyu i tak do beskonechnosti. Podobno trehmernomu toru, fundamental'naya oblast' 1/2-povernutogo kubicheskogo prostranstva mozhet byt' narezana na tonkie vertikal'nye sloi, tak chto pri skleike poluchitsya snova puchok dvuhmernyh torov, s toi tol'ko raznicei, chto na etot raz perednii i zadnii tory skleeny s povorotom na 180 gradusov.

Esli dve grani ishodnogo kuba skleeny s povorotom na 180 gradusov, obrazuetsya 1/2-povernutoe kubicheskoe prostranstvo.

1/4-povernutoe kubicheskoe prostranstvo poluchaetsya tak zhe, kak predydushee, no s povorotom na 90 gradusov. Odnako poskol'ku povorot osushestvlyaetsya tol'ko na chetvert', ono mozhet poluchit'sya ne iz vsyakogo parallelepipeda - ego perednyaya i zadnyaya chasti dolzhny byt' kvadratami, chtoby izbezhat' iskrivleniya i perekashivaniya fundamental'noi oblasti. V perednei grani kuba my uvideli by za svoei kopiei eshe odnu, povernutuyu otnositel'no ee na 90 gradusov.

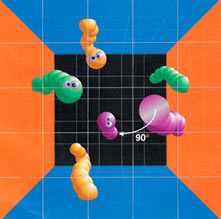Povorot dvuh granei na 90 gradusov daet 1/4-povernutoe kubicheskoe prostranstvo.

1/3-povernutoe shestiugol'noe prizmaticheskoe prostranstvo ispol'zuet v kachestve fundamental'noi oblasti ne kub, a shestiugol'nuyu prizmu. Dlya ego polucheniya nuzhno skleit' kazhduyu gran', predstavlyayushuyu soboi parallelogramm, s ee protivopolozhnoi gran'yu, a dve shestiugol'nye grani - s povorotom na 120 gradusov. Kazhdyi shestiugol'nyi sloi etogo mnogoobraziya - tor, i, takim obrazom, prostranstvo takzhe predstavlyaet soboi puchok torov. Vo vseh shestiugol'nyh granyah my uvideli by kopii, povernutye na 120 gradusov otnositel'no predydushei, a kopii v granyah - parallelogrammah - pryamye.

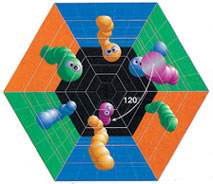Esli v kachestve fundamental'noi oblasti vzyat' shestigrannuyu prizmu, skleit' kazhduyu ee gran' s protivopolozhnoi napryamuyu, a shestiugol'nye torcy s povorotom na 120 gradusov, poluchitsya 1/3-povernutoe shestiugol'noe prizmaticheskoe prostranstvo.

1/6-povernutoe shestiugol'noe prizmaticheskoe prostranstvo skonstruirovano podobno predydushemu, no s toi raznicei, chto perednyaya shestiugol'naya gran' prikleena k zadnei s povorotom na 60 gradusov. Kak i prezhde, v poluchivshemsya puchke torov ostavshiesya grani - parallelogrammy - prikleeny odna k drugoi neposredstvenno.

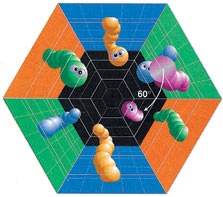Povorot shestiugol'noi grani pered skleikoi na 60 gradusov daet 1/6-povernutoe shestiugol'noe prizmaticheskoe prostranstvo.

Dvoinoe kubicheskoe prostranstvo radikal'no otlichaetsya ot predydushih mnogoobrazii. Eto konechnoe prostranstvo uzhe ne yavlyaetsya puchkom torov i imeet neobychnuyu strukturu skleiki. Dvoinoe kubicheskoe prostranstvo, odnako, ispol'zuet prostuyu fundamental'nuyu oblast', kotoraya predstavlyaet soboi dva kuba, raspolozhennyh odin na drugom. Pri skleike ne vse grani soedinyayutsya napryamuyu: verhnie perednyaya i zadnyaya grani prikleivayutsya k granyam, raspolozhennym neposredstvenno pod nimi. V etom prostranstve my by videli sebya v svoeobraznoi perspektive - stupni nog okazalis' by pryamo pered glazami.

Dvoinoe kubicheskoe prostranstvo.

Na etom zakanchivaetsya spisok konechnyh orientiruemyh evklidovyh trehmernyh, tak nazyvaemyh kompaktnyh mnogoobrazii. Vpolne veroyatno, chto sredi nih i nuzhno iskat' formu nashei Vselennoi.

Mnogie kosmologi polagayut, chto Vselennaya konechna: trudno predstavit' sebe fizicheskii mehanizm vozniknoveniya beskonechnoi Vselennoi. Tem ne menee rassmotrim chetyre ostavshihsya orientiruemyh nekompaktnyh evklidovyh trehmernyh mnogoobraziya, poka ne polucheny real'nye dannye, isklyuchayushie ih sushestvovanie.

Pervoe i samoe prostoe beskonechnoe trehmernoe mnogoobrazie - evklidovo prostranstvo, kotoroe izuchaetsya v srednei shkole (ono oboznachaetsya R³). V etom prostranstve tri osi dekartovyh koordinat prostirayutsya do beskonechnosti. V nem my ne vidim nikakih svoih kopii, ni pryamyh, ni povernutyh, ni perevernutyh.

Sleduyushee mnogoobrazie - tak nazyvaemoe plastinchatoe prostranstvo, fundamental'noi oblast'yu kotorogo sluzhit beskonechnaya plastina. Verhnyaya chast' plastiny, predstavlyayushaya soboi beskonechnuyu ploskost', prikleivaetsya napryamuyu k ee nizhnei chasti, takzhe beskonechnoi ploskosti. Eti ploskosti dolzhny byt' parallel'ny odna drugoi, no mogut byt' proizvol'no sdvinuty pri skleike, chto nesushestvenno, uchityvaya ih beskonechnost'. V topologii eto mnogoobrazie zapisyvaetsya kak R²xS¹, gde R² oboznachaet ploskost', a S¹ - kol'co.

Plastinchatoe prostranstvo voznikaet, esli skleit' verhnyuyu i nizhnyuyu storony beskonechnoi plastiny.

Poslednie dva 3-mnogoobraziya ispol'zuyut v kachestve fundamental'nyh oblastei beskonechno dlinnye trubki. Trubki imeyut chetyre storony, ih secheniya predstavlyayut soboi parallelogrammy, oni ne imeyut ni verha, ni niza - chetyre ih storony prostirayutsya beskonechno. Kak i ran'she, harakter skleiki fundamental'noi oblasti opredelyaet formu mnogoobraziya.

Trubchatoe prostranstvo formiruetsya posredstvom skleiki obeih par protivopolozhnyh storon. Posle skleivaniya pervonachal'noe sechenie v vide parallelogramma stanovitsya dvuhmernym torom. V topologii eto prostranstvo zapisyvaetsya kak proizvedenie T²xR¹.

Povernuv na 180 gradusov odnu iz skleivaemyh poverhnostei trubchatogo prostranstva, poluchim povernutoe trubchatoe prostranstvo. Etot povorot s uchetom beskonechnoi dliny trubki pridaet emu neobychnye harakteristiki. Naprimer, dve tochki, raspolozhennye ochen' daleko odna ot drugoi, po raznym koncam fundamental'noi oblasti, posle skleiki okazhutsya ryadom.

Trubchatye prostranstva - pryamoe (A) i povernutoe (B), v kotorom odna iz poverhnostei skleena s protivopolozhnoi s povorotom na 180 gradusov.

Kakova zhe vse-taki forma nashei Vselennoi?

Chtoby iz privedennyh vyshe desyati evklidovyh 3-mnogoobrazii vybrat' odno v kachestve formy nashei Vselennoi, neobhodimy dopolnitel'nye dannye astronomicheskih nablyudenii.

Proshe vsego bylo by otyskat' kopii nashei Galaktiki v nochnom nebe. Obnaruzhiv ih, my smozhem ustanovit' harakter skleiki fundamental'noi oblasti Vselennoi. Esli okazhetsya, chto Vselennaya predstavlyaet soboi 1/4-povernutoe kubicheskoe prostranstvo, to pryamye kopii nashei Galaktiki budut vidny s chetyreh storon, a povernutye na 90 gradusov - s ostavshihsya dvuh. Odnako, nesmotrya na kazhushuyusya prostotu, etot sposob malo prigoden dlya ustanovleniya formy Vselennoi.

Svet rasprostranyaetsya s konechnoi skorost'yu, poetomu, nablyudaya Vselennuyu, my, v sushnosti, smotrim v proshloe. Dazhe esli my odnazhdy obnaruzhim izobrazhenie nashei Galaktiki, to ne smozhem uznat' ee, potomu chto v svoi "molodye gody" ona vyglyadela sovershenno inache. Slishkom slozhno iz ogromnogo kolichestva galaktik uznat' kopiyu nashei.

V nachale stat'i govorilos', chto Vselennaya imeet postoyannuyu kriviznu. Odnorodnost' kosmicheskogo mikrovolnovogo fonovogo izlucheniya pryamo ukazyvaet na eto. Odnako ono imeet legkie prostranstvennye variacii, primerno 10^-5 kel'vinov, pokazyvayushie, chto v rannei Vselennoi imeli mesto neznachitel'nye fluktuacii plotnosti veshestva. Kogda rasshiryayushayasya Vselennaya ostyvala, materiya v etih oblastyah so vremenem sozdala galaktiki, zvezdy i planety. Karta mikrovolnovogo izlucheniya pozvolyaet posmotret' v proshloe, vo vremena pervonachal'nyh neodnorodnostei, uvidet' nametki Vselennoi, kotoraya byla togda v tysyachu raz men'she. Chtoby ocenit' znachenie etoi karty, rassmotrim gipoteticheskii primer: Vselennaya v vide dvuhmernogo tora.

V trehmernoi Vselennoi my nablyudaem nebo po vsem napravleniyam, to est' v predelah sfery. Dvuhmernye zhiteli dvuhmernoi Vselennoi smogli by nablyudat' ego tol'ko v predelah kruga. Esli by etot krug byl men'she fundamental'noi oblasti ih Vselennoi, oni ne mogli by poluchit' nikakih ukazanii o ee forme. Esli, odnako, krug videniya dvuhmernyh sozdanii bol'she fundamental'noi oblasti, oni smogli by uvidet' peresecheniya i dazhe povtorenie obrazov Vselennoi i popytat'sya naiti tochki s odinakovymi temperaturami, kotorye sootvetstvuyut odnoi i toi zhe ee oblasti. Esli v ih kruge videniya okazalos' by dostatochno mnogo takih tochek, oni smogli by zaklyuchit', chto zhivut v torovoi Vselennoi.

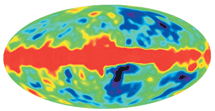Karta raspredeleniya mikrovolnovogo reliktovogo izlucheniya demonstriruet to raspredelenie plotnosti materii, kotoroe bylo 300 tysyach let nazad (pokazano cvetom). Ee analiz pozvolit opredelit', kakuyu topologiyu imeet Vselennaya.

Nesmotrya na to, chto my zhivem v trehmernoi Vselennoi i vidim sfericheskuyu oblast', pered nami vstaet ta zhe problema, chto i pered dvuhmernymi sozdaniyami. Esli nasha sfera videniya men'she fundamental'noi oblasti Vselennoi 300 000-letnei davnosti, my nichego neobychnogo ne uvidim. V protivnom sluchae sfera budet peresekat' ee po krugam. Obnaruzhiv dva kruga, imeyushih odinakovye variacii mikrovolnovogo izlucheniya, kosmologi smogut sravnit' ih orientaciyu. Esli krugi raspolozheny krest-nakrest, eto budet oznachat' nalichie skleiki, no bez povorota. Nekotorye iz nih, odnako, mogut sochetat'sya v sootvetstvii s povorotom na chetvert' ili na polovinu. Esli etih krugov udastsya obnaruzhit' dostatochno mnogo, taina fundamental'noi oblasti Vselennoi i ee skleiki budet raskryta.

Odnako do teh por, poka ne poyavitsya tochnaya karta mikrovolnovogo izlucheniya, kosmologi nikakih zaklyuchenii sdelat' ne smogut. V 1989 godu issledovateli iz NASA popytalis' sozdat' kartu reliktovogo izlucheniya kosmicheskogo prostranstva. Odnako uglovoe razreshenie sputnika sostavlyalo poryadka 10 gradusov, chto ne pozvolilo sdelat' tochnye izmereniya, udovletvoryayushie kosmologov. Vesnoi 2002 goda NASA predprinyalo vtoruyu popytku i zapustilo zond, kotoryi nanes na kartu temperaturnye fluktuacii s uglovym razresheniem uzhe poryadka 0,2 gradusa. V 2007 godu Evropeiskoe kosmicheskoe agentstvo planiruet ispol'zovat' sputnik "Plank", imeyushii uglovoe razreshenie 5 dugovyh sekund.

Esli zapuski proidut uspeshno, to v techenie chetyreh-desyati let budut polucheny tochnye karty fluktuacii reliktovogo izlucheniya. I esli razmer sfery nashego videniya okazhetsya dostatochno bol'shoi, a izmereniya - dostatochno tochnymi i nadezhnymi, my nakonec uznaem, kakuyu formu imeet nasha Vselennaya.

Publikacii s klyuchevymi slovami: Kosmologiya - topologiya - topologiya Vselennoi Publikacii so slovami: Kosmologiya - topologiya - topologiya Vselennoi
Sm. takzhe: Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Kuda smeshaetsya krasnoe smeshenie? Samaya dalekaya sverhnovaya tipa Ia Rashid Alievich Syunyaev (k semidesyatiletiyu so dnya rozhdeniya) Vse publikacii na tu zhe temu >>