Sverhsvetovoe razbeganie galaktik i gorizonty Vselennoi: putanica v tonkostyah

Sergei Popov

Vvedenie

V Prirode ochen' mnogo udivitel'nogo, i pytat'sya vydelit' samoe-samoe zanyatie neblagodarnoe. Kto-to polagaet, chto Zhizn' - samoe udivitel'noe v Prirode. Kto-to - chto Razum. Esli obratit'sya k nezhivoi prirode, to kto-to skazhet ob udivitel'nyh zakonah mikromira, kto-to o processah samoorganizacii i haose. No, navernoe, esli sostavlyat' spisok, to vsegda v desyatku samyh udivitel'nyh fenomenov budet popadat' rasshirenie Vselennoi.

My ne budem zdes' obsuzhdat' obosnovannost' vyvodov o rasshirenii Vselennoi na osnove kosmologicheskih nablyudenii. Ravno, my ne budem obsuzhdat' osnovy special'noi i obshei teorii otnositel'nosti (STO i OTO). Esli ostavit' v storone vopros o "samom nachale", kotorye nas zdes' ne budet sushestvenno zanimat' (my budem polagat' pod "nachalom" dostatochno dalekii moment vremeni - skazhem, do pervichnogo nukleosinteza - chtoby ne vdavat'sya v spekulyacii ob ochen' rannei Vselennoi, esli ugodno, to mozhno polagat' "nachalom" - moment okonchaniya inflyacionnoi stadii, esli ona byla), to somnenii v dannyh o rasshirenii Vselennoi net, kak net bol'shih somnenii v primenimosti OTO v etom sluchae (vsyakie vozmozhnye effekty kvantovoi gravitacii i t.p. tut nevazhny). My budem obsuzhdat' standartnuyu kartinu, sleduya v osnovnom nedavnei stat'e Tamary Devis (Tamara M. Davis) i Charl'za Lainvivera (Charles H. Lineweaver) "Expanding confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe" i knige Edvarda Garrisona (Edward Harrison) "Cosmology: the science of the universe". Stoit takzhe upomyanut' raboty Kianga - T. Kiang - "Time, Distance, Velocity, Redshift: a personal guided tour", "Can We Observe Galaxies that Recede Faster than Light ? - A More Clear-Cut Answer". Krome togo, obsuzhdaemye voprosy razobrany vo mnogih uchebnikah i monografiyah po kosmologii.

Tonkie detali

Rasshirenie Vselennoi (my budem pisat' Vselennuyu s bol'shoi bukvy, hotya rech' idet imenno o nablyudaemom mire, kotoryi inogda pishut s malen'koi bukvy) yavlyaetsya ochen' strannym processom, osmyslenie kotorogo vo-pervyh vyzyvaet opredelennyi intellektual'nyi diskomfort, vo-vtoryh privodit k nekotoroi putanice. Bezuslovno, putanica v golovah ne otnositsya k professional'nym kosmologam i tem, kto ser'ezno razbiralsya s etimi voprosami (v standartnyh uchebnikah po kosmologii vse obychno akkuratno raspisano). Odnako, v populyarnoi literature netochnosti prisutstvuyut v izbytke. Devis i Lainviver, ni v koei mere ne pretenduya na otkrytie novogo fenomena, popytalis' obsudit' osnovnye netochnosti, svyazannye s populyarnym (i ne tol'ko) izlozheniem nekotoryh detalei, svyazannyh s rasshireniem Vselennoi, i na nash vzglyad im eto udalos'. Tak chto ih rabota nosit skoree prosvetitel'sko-pedagogicheskii harakter. V prilozhenii k svoei stat'e oni privodyat citaty iz izvestnyh knig izvestnyh lyudei, gde v toi ili inoi stepeni netochno opisany eti detali (ne otnosya sebya k chislu velikih, nel'zya ne otmetit', chto i my v svoe vremya vnesli vklad v rasprostranenie putannyh znanii, o chem ves'ma sozhaleem). Zabegaya vpered skazhem, chto osnovnym istochnikom putanicy yavlyaetsya ispol'zovanie formuly dlya relyativistskogo effekta Doplera tam, gde ee primenyat' nel'zya.

Obsudim dve detali: sverhsvetovoe rasshirenie (kogda skorost' udaleniya galaktiki prevyshaet svetovuyu) i gorizonty. V etom nam budut pomogat' risunki iz stat'i Devis i Lainvivera.

Teoreticheskoe vvedenie

V nachale nemnogo poyasnenii.

Budem ispol'zovat' metriku Robertsona-Uokera v uproshennom variante:

Zdes' χ-soputstvuyushaya koordinata. Dlya dvuh galaktik (v prenebrezhenii pekulyarnymi skorostyami) eta velichina ne izmenyaetsya. Dlya rasprostranyayushegosya fotona ona, konechno zhe, izmenyaetsya (pekulyarnaya skorost' fotona ravna skorosti sveta). Zato dlya fotona ds=0, a potomu my mozhem zapisat' dlya nego cdt=R(t)dχ. R(t) - masshtabnyi faktor. V rasshiryayusheisya Vselennoi on uvelichivaetsya so vremenem, otrazhaya process rasshireniya. Naprimer R(t₀)/R(t)=3 pokazyvaet, chto s momenta t po moment t₀ vse sobstvennye rasstoyaniya mezhdu ob'ektami s nulevymi pekulyarnymi skorostyami ( χ=const) vyrosli v tri raza. Proizvedenie masshtabnogo faktora na soputstvuyushuyu koordinatu nazyvaetsya sobstvennym rasstoyaniem (proper distance), my budem oboznachat' ego D, D=R(t) χ. Imenno eto rasstoyanie yavlyaetsya "nashim obychnym" ponyatiem. Krome togo, mozhno vvesti eshe t.n. konformnoe vremya, τ:

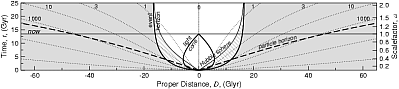
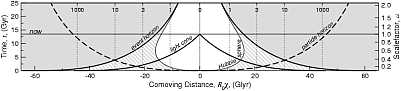
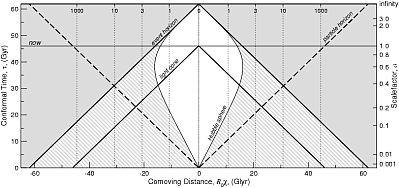
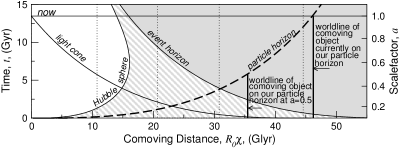
Naryadu s obychnym vremenem eti velichiny ispol'zovany dlya postroeniya risunkov vnizu. Po vertikal'noi osi otlozheno vremya, po gorizontal'noi - rasstoyanie. Mirovye linii "galaktik" otmecheny punktirom. Oni pronumerovany krasnym smesheniem v nastoyashii moment vremeni (v kosmologii krasnoe smeshenie svyazano ne so skorost'yu napryamuyu, ono opredelyaetsya formuloi: 1+z=R(t₀)/R(t), obratite vnimanie, krasnoe smeshenie dannogo ob'ekta izmenyaetsya so vremenem, v raznyh modelyah ono mozhet kak rasti tak i umen'shat'sya). "Nam" sootvetstvuet liniya χ=0 (i, razumeetsya, D=0). Kak vidno na vtorom (1b) i tret'em (1v) risunkah, pri ispol'zovanii soputstvuyushego rasstoyaniya mirovye linii vseh "galaktik" yavlyayutsya pryamymi liniyami. Na pervom risunke (1a) vidno rasshirenie Vselennoi: mirovye linii "galaktik" udalyayutsya ot nas - sobstvennoe rasstoyanie rastet.

Napomnim, chto postoyannaya Habbla yavlyaetsya velichinoi, izmenyayusheisya so vremenem. Ona ravna otnosheniyu proizvodnoi masshtabnogo faktora po vremeni k samomu masshtabnomu faktoru: H=(dR/dt)/R. Skorost' ubeganiya opredelyaetsya kak proizvodnaya sobstvennogo rasstoyaniya:

Zdes' my takzhe raspisali, kak skorost' ubeganiya vyrazhaetsya cherez raznye velichiny. Sredi vypisannyh vyrazhenii est' i V_rec=H(t)D(t). Zakon Habbla. Otmetim, chto eto vyrazhenie sleduet iz kosmologicheskogo principa (Vselennaya odnorodna, izotropna i vyglyadit odinakogo dlya lyubogo nablyudatelya v dannyi moment vremeni). Esli by Habbl smog v svoe vremya promerit' krasnye smesheniya i opredelit' rasstoyaniya do z>1, to obnaruzhilos' by otklonenie ot prostogo zakona, t.k. v podhode Habbla dlya opredeleniya skorosti po krasnomu smesheniyu ispol'zovalsya zakon Doplera. Esli by Habbl smog doiti do bol'shih krasnyh smeshenii i ispol'zoval by v etom sluchae dlya opredeleniya skorosti relyativistskii zakon Doplera, to krasivaya pryamaya sootnosheniya Habbla nachala by iskrivlyat'sya. Mezhdu tem, esli ispol'zovat' OTO, to vse budet v poryadke: vyrazhenie V_rec=H(t)D(t) sohranyaet svoyu silu dlya lyubyh krasnyh smeshenii.

V kosmologii byvaet opasno primenyat' STO (i intuiciyu na ee osnove), t.k. eto mozhet privodit' k oshibochnym vyvodam (Kiang nazyvaet eto "teni STO"). Delo v tom, chto skorost' ubeganiya sushestvenno otlichaetsya ot privychnogo nam ponyatiya skorosti. Dlya nee STO neprimenima "v lob". Skorost' ubeganiya yavlyaetsya ne svoistvom istochnika, a svoistvom tochki v prostranstve. Poetomu ne sleduet zhdat' pryamoi primenimosti ponyatii, intuitivno narabotannyh v STO, k kosmologii.

Ochevidno, chto est' rasstoyanie - sfera Habbla, D_H, - na kotorom skorost' ubeganiya ravna skorosti sveta. Prichem, kak budet pokazano nizhe, my mozhem videt eti ob'ekty (konechno, nuzhno uchest', chto svetu nuzhno vremya - i dovol'no bol'shoe - chtoby dobrat'sya do nas ot etih ob'ektov). Eto udivitel'nyi fakt ni chemu ne protivorechit (v tom chisle i STO, kotoruyu tut prosto nel'zya primenyat').

Sverhsvetovoe rasshirenie

Obsudim vozmozhnost' nablyudeniya "sverhsvetovyh galaktik". V nachale pogovorim o svetovom konuse. Impul's sveta ot istochnika mozhet dostignut' nas, esli istochnik v moment izlucheniya lezhit vnutri svetovogo konusa (esli on lezhit na svetovom konuse, to my vidim ego seichas, esli vnutri - to my videli ego ran'she). V "normal'nyh" koordinatah (verhnii risunok) svetovoi konus prevrashaetsya v kapleobraznuyu figuru. Eto svyazano s rasshireniem Vselennoi. Esli my myslenno poidem po svetovomu luchu, prishedshemu k nam ot dalekoi galaktiki, nazad po vremeni (na risunke eto dvizhenie vniz), to sobstvennoe rasstoyanie (i soputstvuyushee) do etoi galaktiki budet, estestvenno, umen'shat'sya. V nachale oba rasstoyaniya ot nashei Galaktiki budut uvelichivat'sya (eto poka normal'no, my zhe "uhodim" ot nashei Galaktiki), no potom kartina dlya sobstvennogo rasstoyaniya nachnet izmenyat'sya: soputstvuyushee rasstoyanie budet uvelichivat'sya, a vot sobstvennoe nachnet umen'shat'sya . Dvizhenie v proshloe sootvetstvuet szhatiyu Vselennoi, sobstvennoe rasstoyanie (D=R(χ₁ - χ₂)) mezhdu dvumya tochkami s zadannymi soputstvuyushimi koordinatami (χ₁ i χ₂) budet umen'shat'sya za schet umen'sheniya masshtabnogo faktora R(t). Poetomu i svetovoi konus na ris 1a budet "zakruglyat'sya" (bolee krupno eto vidno na risunke 2a). Na risunke 1v (gde po vertikal'noi osi otlozheno konformnoe vremya) svetovoi konus vedet sebya privychnym obrazom (predostavlyaem chitatelyu samomu s etim razobrat'sya), i yasno vidno, chto obychnaya logika imeet mesto - na bol'shih krasnyh smesheniyah my vidim seichas ob'ekty s bolee dalekim soputstvuyushim rasstoyaniem (a znachit, v nastoyashii moment eti ob'ekty dal'she ot nas, chem ob'ekty s men'shimi z).

Teper' posmotrim, kak vedet sebya Habblovskaya sfera. Zdes' vse privychno, v "normal'nyh" koordinatah ona umen'shaetsya pri dvizhenii v proshloe. Odnako, pri pererisovyvanii v soputstvuyushih koordinatah kartina menyaetsya (i eto pomogaet proyasnit' smysl proishodyashego). Esli my ispol'zuem soputstvuyushee rasstoyanie, to habblovskaya sfera vedet sebya nemonotonno! Na tret'em risunke (1v) yasno vidno, chto dlya dannoi konkretnoi modeli (30/70) istochniki mogut popadat' v Habblovskuyu sferu, a potom vyhodit' iz nee.

I vot - samoe interesnoe. Kak horosho vidno, na nashem svetovom konuse est' istochniki, kotorye i v moment izlucheniya, i v nastoyashii moment nahodyatsya za predelami nashei Habblovskoi sfery, t.e. ih skorost' ubeganiya vyshe svetovoi i v moment ispuskaniya, i seichas. Dlya modeli 30/70 vse istochniki s z>1.46 v nastoyashii moment udalyayutsya ot nas bystree skorosti sveta. V modeli s zamedleniem rasshireniya iz fakta prevysheniya skorosti sveta v nastoyashii moment avtomaticheski sleduet prevyshenie i v moment ispuskaniya izlucheniya.

Kak eto mozhet byt'? Voobshe govorya, to, chto my seichas vidim ispushennyi davnym davno svet, a sami istochniki seichas udalyayutsya ot nas so sverhsvetovoi skorost'yu, ne dolzhno vyzyvat' udivleniya. Bolee interesno to, chto my takzhe vidim svet istochnikov, kotorye v moment izlucheniya imeli skorost' ubeganiya bol'she svetovoi, a svet ot nih vse ravno k nam popal. Poprobuem eto proyasnit' i budem ispol'zovat' dlya naglyadnosti sferu Habbla. Zdes' vazhno sravnit' dve veshi: kak v dannyi moment vremeni vedet sebya Habblovskaya sfera (skorost' ee rasshireniya, dD_H/dt) i skorost' ubeganiya fotona (V_rec -c). Esli dD_H/dt > V_rec -c, to foton rano ili pozdno popadet vnutr' Habblovskoi sfery i smozhet dostich' nas. T.e. vazhno ponyat', polozhitel'na ili otricatel'na skorost' fotona otnositel'no granicy sfery Habbla. Obratite vnimanie (ris 1a i 2a), chto sobstvennoe rasstoyanie ot nas do fotona, dvigayushegosya po nashemu svetovomu konusu, uvelichivaetsya poka foton nahoditsya vne sfery Habbla, i umen'shaetsya vnutri nee.

My posvyatili stol'ko vremeni razboru sfery Habbla ne potomu, chto eto kakoe-to ochen' vazhnoe postroenie - mozhno prekrasno oboitis' voobshe bez vvedeniya etogo ponyatiya. Naprimer, do nas dohodyat (doshli ili doidut) fotony, kotorye byli ispusheny vnutri svetovogo konusa, provedennogo iz nashego beskonechnogo budushego. Chtoby eto ponyat' i ob'yasnit' nikakaya sfera Habbla ne nuzhna. Odnako, "dzhinn uzhe vypushen iz butylki": sfera Habbla, kak rasstoyanie, na kotorom skorost' ubeganiya ravna skorosti sveta, prochno voshla v populyarnuyu literaturu. A potomu vazhno ponimat' "chto eto za zver'".

Tipichnaya putanica so sverhsvetovymi skorostyami ubeganiya i vozmozhnost'yu nablyudeniya takih istochnikov svyazana s tem, chto ispol'zuyut formulu dlya relyativistskogo effekta Doplera, v kotoroi stremlenie krasnogo smesheniya k beskonechnosti sootvetstvuet stremleniyu skorosti k skorosti sveta. T.o., govoryat, sleduya etomu zabluzhdeniyu: "nablyudat' galaktiki, ubegayushie so skorost'yu bol'she svetovoi, nel'zya, t.k. oni nahodyatsya za gorizontom". Na samom dele oni nahodyatsya za sferoi Habbla, kotoraya ne yavlyaetsya gorizontom, a potomu ih mozhno prekrasno nablyudat'. V nekotoryh modelyah gorizont i sfera Habbla mogut sovpadat', no, po vsei vidimosti, my zhivem vo Vselennoi, gde gorizont shire sfery Habbla.

Krasnoe smeshenie pozvolyaet opredelit' ne skorost', a soputstvuyushee rasstoyanie (esli zadana model'). Soputstvuyushee rasstoyanie, χ, kak funkciya z zadaetsya proizvedeniem (c/R₀) na integral ot nulya do z, pod integralom stoit dz'/H(z'). V ryade kosmologicheskih modelei beskonechnoe krasnoe smeshenie budet sootvetstvovat' beskonechnomu soputstvuyushemu rasstoyaniyu. V modeli 30/70 beskonechnoe krasnoe smeshenie sootvetstvuet ob'ektu na gorizonte chastic s konechnym soputstvuyushim rasstoyaniem ot nas. Kak legko ponyat' nulevoe znachenie masshtabnogo faktora v moment izlucheniya budet davat' beskonechnoe krasnoe smeshenie, t.e. eto sootvetstvuet istochniku na t=0 (R(t=0)=0).

Otmetim takzhe (sm. ris), chto rasstoyanie do dalekih ob'ektov nel'zya ocenivat', umnozhaya skorost' sveta na {(vozrast Vselennoi seichas)-(vozrast Vselennoi v moment izlucheniya)}. Sobstvennoe rasstoyanie sushestvenno vyshe. Chasto mozhno prochest', chto "t.k. vozrast Vselennoi poryadka 13 milliardov let, to rasstoyanie do samyh dalekih iz nablyudaemyh galaktik poryadka 12 milliardov svetovyh let". Eto neverno. Naprimer, rasstoyanie do ob'ekta s z=10 v modeli, privedennoi na risunkah, budet okolo 30 milliardov svetovyh let (rasstoyanie zhe mezhdu nami v moment izlucheniya bylo gorazdo men'she, i sostavlyalo neskol'ko milliardov svetovyh let). Obratite vnimanie na masshtab shkaly dlya samyh bol'shih rasstoyanii na Karte Vselennoi.

Obychnaya zhe intuiciya primenima na malyh rasstoyaniyah. Primerno do z=0.1 rezul'taty po vypisannym vyshe formulam i po effektu Doplera budut blizki drug k drugu. Takzhe dlya takih blizkih istochnikov mozhno ocenivat' rasstoyaniya umnozhaya skorost' sveta na {(vozrast Vselennoi seichas)-(vozrast Vselennoi v moment izlucheniya)}.

Gorizonty

S gorizontami bol'shoi putanicy v literature net. Prosto polezno razobrat'sya. Rassmotrim dva vazhnyh gorizonta: gorizont chastic i gorizont sobytii.

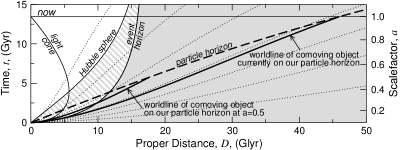
Gorizont chastic - eto rasstoyanie do samogo dalekogo istochnika, v principe nablyudaemogo v dannyi moment vremeni (na vsyakii sluchai utochnim, chto rech' idet o rasstoyanii do ob'ekta v moment priema fotona, a ne v moment izlucheniya). Inogda etot radius opredelyayut po-drugomu: rasstoyanie, kotoroe foton mozhet proiti ot t=0 do dannogo momenta (t.e. eto rasstoyanie, na kotoroe mozhno peredat' informaciyu za vremya, ravnoe vozrastu Vselennoi). Iz ris. 1v horosho vidno, chto oba opredeleniya ekvivalentny. V nerasshiryayusheisya Vselennoi konechnogo vozrasta (t.e. s "nachalom") etot radius lineino ros by so vremenem. Vo Vselennoi, rasshiryayusheisya s zamedleniem, radius ros by vsegda, no medlennee. V uskoryayusheisya Vselennoi radius stremitsya k konechnomu znacheniyu (v soputstvuyushih koordinatah) pri stremlenii vremeni k beskonechnosti (t.e. est' ob'ekty, kotorye my nikogda ne uvidim, skol'ko by ni zhdali). Etot gorizont nel'zya opredelit' kak skorost' sveta, umnozhennuyu na vremya posle nachala rasshireniya. Soputstvuyushaya koordinata ob'ekta na gorizonte chastic v moment t opredelyaetsya kak skorost' sveta, umnozhennaya na intergral ot 0 do dannogo vremeni t, pod integralom stoit dt'/R(t') - konformnoe vremya. Sootvetstvenno, dlya opredeleniya sobstvennogo rasstoyaniya nado potom umnozhit' rezul'tat na masshtabnyi faktor v dannyi moment. Obratite vnimanie, krasnoe smeshenie istochnikov na gorizonte chastic beskonechno.

Na risunkah gorizont chastic proillyustrirovan svetovym konusom iz tochki t=0, χ=0 v budushee. Odnako, etot konus sam po sebe ne yavlyaetsya gorizontom chastic! V kazhdyi dannyi moment t_i gorizont yavlyaetsya secheniem etogo konusa ploskost'yu t=t_i. T.e. eto trehmernaya sfera vokrug nas, kotoraya izmenyaetsya s techeniem vremeni. Zato narisovannyi konus pozvolyaet uvidet', kak gorizont chastic izmenyaetsya so vremenem (v chastnosti, kak "galaktiki" vhodyat v nego, t.e. stanovyatsya vidimymi dlya nas).

Gorizont sobytii - dovol'no hitroe ponyatie (i ne vo vsyakoi kosmologicheskoi modeli on sushestvuet). Davaite eshe raz posmotrim na ris. 1v. Krome nashego svetovogo konusa (dlya nastoyashego momenta vremeni), my vidim svetovoi konus dlya momenta v beskonechnom budushem - eto i est' gorizont sobytii. On delit' ploskost' (prostranstvo-vremya) na dve chasti. Sobytiya vnutri konusa (napomnim, chto tochka na etoi ploskosti - eto imenno sobytie v prostranstve I vremeni) delyatsya na dve gruppy. Te, chto nahodyatsya vnutri konusa ili byli dostupny nam dlya nablyudeniya v proshlom, ili zhe budut dostupny v budushem. Sobytiya vne konusa nam principial'no nedostupny dlya nablyudenii.

Obratite vnimanie, chto v modeli 30/70 beskonechnomu budushemu sootvetstvuet konechnoe konformnoe vremya.

Poprobuem dat' nekotoroe dopolnenie/poyasnenie pro gorizont sobytii. Rasstoyanie do gorizonta sobytii v nastoyashii moment - eto rasstoyanie do chasticy, do kotoroi mozhet doiti nash svetovoi signal, poslannyi v dannyi moment. Na ris. 1v vidno, chto, esli my prodolzhim nash svetovoi konus v budushee, to on popadet na verhnyuyu gorizontal' v tochke, kotoraya nahoditsya na takom zhe soputstvuyushem rasstoyanii, na kakom konus iz beskonechnogo budushego peresekaet nashu gorizontal' ("now"). Ili mozhno skazat' tak: svetovoi konus chasticy na gorizonte sobytii peresechet nashu mirovuyu liniyu v beskonechnom budushem.

Na risunke 2b vidno, chto dlya soputstvuyushego rasstoyaniya gorizont sobytii sokrashaetsya. I eto ponyatno. Vo Vselennoi, kotoraya rasshiryatsya uskorenno, so vremenem signalu vse "trudnee i trudnee" dobrat'sya do dalekih galaktik - oni udalyayutsya slishkom bystro (a budut eshe bystree). Soputstvuyushee rasstoyanie do chasticy na etom gorizonte opredelyaetsya kak proizvedenie skorosti sveta na integral ot dannogo momenta vremeni do "konca" (do beskonechnosti), pod integralom, kak i vyshe, dt'/R(t').

Zaklyuchenie

Vyshe my postaralis' proyasnit' nekotorye tonkie momenty, svyazannye s rasshireniem Vselennoi. My mozhem nablyudat' (i nablyudaem) istochniki, kotorye i v moment izlucheniya, i seichas imeyut skorost' ubeganiya, prevyshayushuyu skorost' sveta. Rasstoyaniya do dalekih ob'ektov prevyshayut proizvedenie skorosti sveta i vozrasta Vselennoi. Rasstoyanie, na kotorom skorost' ubeganiya sravnivaetsya so svetovoi, ne yavlyaetsya gorizontom (t.e. granicei vidimoi chasti Vselennoi), i voobshe ne yavlyaetsya fizicheski vydelennym rasstoyaniem (ob'ekty pryamo pered etoi granicei i pryamo za nei nichem ne otlichayutsya principial'no, kak ne otlichayutsya i usloviya ih nablyudenii). Gorizontom nablyudaemoi Vselennoi yavlyaetsya gorizont chastic, na nem istochniki imeyut beskonechnye krasnye smesheniya.

Vyrazhayu glubokuyu priznatel'nost' S.Blinnikovu, P.Ivanovu, M.Prohorovu za ryad cenneishih zamechanii.

Publikacii s klyuchevymi slovami: Kosmologiya - Rasshirenie Vselennoi Publikacii so slovami: Kosmologiya - Rasshirenie Vselennoi
Sm. takzhe: Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Kuda smeshaetsya krasnoe smeshenie? Ne bogi rasshirenie vselennoi nablyudayut Samaya dalekaya sverhnovaya tipa Ia Vse publikacii na tu zhe temu >>