Matematika trehmernyh mnogoobrazii
1.09.1984 16:02 | U. P. Terston, D. R. Uiks/"V Mire Nauki"

Matematika trehmernyh mnogoobrazii

Uil'yam P.Terston, Dzheffri R.Uiks

("V mire nauki", N9, 1984)

Tysyachi let nazad lyudi dumali, chto Zemlya ploskaya. Eto dolzhno bylo kazat'sya sovershenno ochevidnym lyubomu nablyudatelyu v okeane ili prerii; obsuzhdalsya ne lishennyi smysla vopros, beskonechna li Zemlya ili u nee est' krai. Seichas ponyatno, kak moglo vozniknut' takoe v korne oshibochnoe predstavlenie: dazhe s vysoty neskol'kih tysyach metrov nebol'shaya chast' zemnoi poverhnosti, imeyushei priblizhenno sfericheskuyu formu, vyglyadit kak nebol'shoi uchastok ploskosti. Rezhe otdayut sebe otchet v tom, chto beschislennoe kolichestvo drugih form zemnoi poverhnosti pri lokal'nom nablyudenii vyglyadelo by tochno tak zhe. Naprimer, esli ishodit' iz takih lokal'nyh nablyudenii, Zemlya mogla by imet' formu nepravil'noi kapli ili bublika.

Issledovaniya v toi oblasti matematiki, kotoraya nazyvaetsya topologiei, ob'yasnyayut, chto s takoi zhe situaciei my stalkivaemsya pri popytkah opisat' formu Vselennoi v celom na osnovanii nablyudenii ogranichennoi ee chasti, vidimoi iz nashei tochki prostranstva. Nablyudatel', nahodyashiisya na Zemle, ne mozhet s uverennost'yu sdelat' vyvod, chto Vselennaya na vsem beskonechnom protyazhenii sohranyaet geometricheskuyu strukturu obychnogo evklidova prostranstva, hotya do sih por net osnovanii i dlya protivopolozhnogo utverzhdeniya. Esli zhe geometriya Vselennoi ne yavlyaetsya evklidovoi, to kakovy al'ternativy? Odna horosho izvestnaya ideya sostoit v tom, chto prostranstvo "iskrivleno" pochti takim zhe obrazom, kak mozhet byt' iskrivlena poverhnost'. Trehmernaya krivizna prostranstva i tesno svyazannaya s nei chetyrehmernaya krivizna prostranstva-vremeni stali vazhnymi ponyatiyami v astronomii i kosmologii, poskol'ku oni igrayut klyuchevuyu rol' v obshei teorii otnositel'nosti Einshteina.

Tem ne menee opredelenie odnoi tol'ko krivizny ne dostatochno dlya opisaniya togo, chto my nazyvaem formoi Vselennoi. Nekotorye vozmozhnye tipy trehmernoi struktury Vselennoi mozhno opisat' po analogii s dvumernymi poverhnostyami, no eta analogiya lish' navodit na mysl' o bogatstve i raznoobrazii form, poyavlyayushihsya pri dobavlenii tret'ego izmereniya. V deistvitel'nosti, poskol'ku prostranstvo i vremya v teorii otnositel'nosti rassmatrivayutsya kak edinoe celoe, nazyvaemoe prostranstvom-vremenem, mozhno predpolozhit', chto adekvatnoe matematicheskoe opisanie Vselennoi dolzhno byt' chetyrehmernym. Odnako est' osnovaniya nadeyat'sya, chto struktura chetyrehmernogo prostranstva-vremeni opredelyaetsya strukturoi ego trehmernoi prostranstvennoi chasti. Poetomu, chtoby bez predubezhdeniya izuchat' strukturu Vselennoi v celom, nuzhno nachat' s izucheniya tipov trehmernyh ob'ektov, geometricheskie svoistva kotoryh mogli by nahodit'sya v soglasii so svoistvami nablyudaemoi Vselennoi. Takie ob'ekty nazyvayutsya trehmernymi mnogoobraziyami ili 3-mnogoobraziyami.

Izuchenie 3-mnogoobrazii v nekotorom smysle obobshaet izuchenie 2-mnogoobrazii, ili poverhnostei. No esli opisanie i klassifikaciya vseh 2-mnogoobrazii izvestny topologam uzhe bolee sta let, to sistematicheskaya klassifikaciya vseh 3-mnogoobrazii do sih por ostaetsya nereshennoi problemoi vvidu chrezvychainoi slozhnosti form nekotoryh iz nih. Meru slozhnosti mnogoobraziya podskazyvaet matematicheskaya procedura, nazyvaemaya hirurgiei. Hirurgiya pozvolyaet postroit' 3-mnogoobrazie po lyuboi sputannoi verevochnoi petle nezavisimo ot togo, naskol'ko ona zauzlena. Predstavim sebe, chto sravnivayutsya dva sputannyh motka nitok ili rybolovnoi leski, i nuzhno uznat', v tochnosti li odinakovym sposobom oni pereputany. Esli net sposoba sistematicheskoi klassifikacii takih zaputannyh motkov, to net nadezhdy i na uspeh v izuchenii 3-mnogoobrazii. Poetomu do nedavnego vremeni matematiki imeli malo osnovanii schitat', chto mozhno postroit' sistematicheskuyu teoriyu 3-mnogoobrazii.

Seichas takoe pessimisticheskoe zaklyuchenie sleduet peresmotret'. Issledovaniya odnogo iz nas (Terstona) po geometrii 3-mnogoobrazii pokazyvayut, chto sushestvuet shema, kotoraya mozhet privesti k ponimaniyu struktury vsevozmozhnyh 3-mnogoobrazii. Vse izvestnye 3-mnogoobraziya ukladyvayutsya v etu shemu, i v rezul'tate udaetsya opisat' v geometricheskih terminah ih skruchivanie i izgibanie.

Teoriya mnogoobrazii voznikla v XIX v. v svyazi s potrebnost'yu geometricheskoi interpretacii kolichestvennyh sootnoshenii. Naprimer, mnozhestvo reshenii uravneniya s dvumya neizvestnymi mozhno izobrazit' kak nekotoroe mnozhestvo tochek na ploskosti. Kazhdaya tochka otvechaet pare znachenii neizvestnyh, udovletvoryayushih dannomu uravneniyu; v tipichnyh sluchayah eto mnozhestvo tochek predstavlyaet soboi krivuyu ili neskol'ko krivyh. Podobno etomu, mnozhestvo reshenii uravneniya s tremya neizvestnymi obychno mozhno izobrazit' v vide dvumernoi poverhnosti v trehmernom prostranstve, naprimer, takoi, kak poverhnost' sfery. Dlya uravnenii bolee chem s tremya neizvestnymi mnozhestvo reshenii mozhno geometricheski opisat' takim zhe obrazom: eto mnogoobrazie bolee vysokoi razmernosti, lezhashee v prostranstve eshe bol'shego chisla izmerenii. Hotya takie ob'ekty naglyadno predstavit' nel'zya, matematiki razrabotali kachestvennye metody dlya issledovaniya uravnenii, privodyashih k mnogoobraziyam vysokoi razmernosti.

V deistvitel'nosti topologiya D ne v sostoyanii reshat' uravneniya. Zato ona predostavlyaet matematicheskii slovar': prilagatel'nye i sushestvitel'nye, s pomosh'yu kotoryh mozhno opisyvat' obshie svoistva mnozhestva reshenii bez ego fakticheskogo opredeleniya. Tak, hotya mnogoobrazie tochek, izobrazhayushih resheniya kakogo-to uravneniya, imeet vpolne opredelennuyu formu, predmetom izucheniya topologii yavlyayutsya ne svoistva etoi konkretnoi formy, a tol'ko te svoistva, kotorye sohranyayutsya pri lyubyh deformaciyah etogo mnogoobraziya, vypolnyaemyh bez razrezov, razryvov ili prokolov.

Bublik mozhno prevratit' v kofeinuyu chashku, esli sdelat' vmyatinu na ego poverhnosti, a zatem uvelichivat' etu vmyatinu, odnovremenno szhimaya ostal'nuyu chast' bublika. Soglasno staroi shutke, topolog - eto chelovek, kotoryi ne otlichaet bublik ot kofeinoi chashki (s ruchkoi). Odnako topolog navernyaka otlichit poverhnost' bublika ot poverhnosti stakana bez ruchek, poskol'ku ni odnu iz nih nel'zya nepreryvno deformirovat' v druguyu. Mozhet pokazat'sya, chto, dopuskaya proizvol'nye deformacii, topologiya otbrasyvaet samye interesnye svoistva mnogoobraziya. Odnako vo mnogih matematicheskih voprosah topologicheskaya informaciya igraet vazhnuyu rol'.

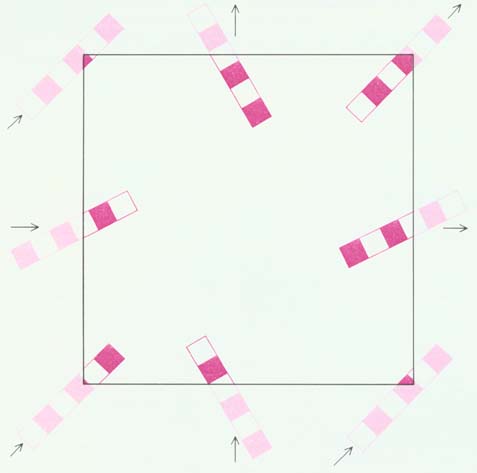
Ris. 1. Topologicheskaya struktura Vselennoi ne obyazana sovpadat' so strukturoi beskonechnogo trehmernogo evklidova prostranstva. Matematicheskaya teoriya trehmernyh mnogoobrazii pokazyvaet, chto prostranstvo mozhet "iskrivlyat'sya samo v sebe" beskonechnym chislom sposobov. Odnoi iz vozmozhnyh modelei topologii prostranstva sluzhit trehmernoe mnogoobrazie, otkrytoe G. Zeifertom i K. Ve-berom v 1932 g. Takoe mnogoobrazie nel'zya naglyadno izobrazit' "izvne", potomu chto dlya etogo prishlos' by "vzglyanut'" na nego iz chetvertogo ili bolee vysokogo izmereniya. Tem ne menee ego mozhno myslenno predstavit' sebe kak dodekaedr, protivopolozhnye grani kotorogo matematicheski skleeny drug s drugom, t.e. otozhdestvleny. Raskrashennye planki, dvizhushiesya skvoz' grani dodekaedra vnutr' i naruzhu, pokazyvayut, kak skleivat' grani: odna gran' iz kazhdoi pary protivopolozhnyh granei povorachivaetsya vokrug osi, perpendikulyarnoi ee ploskosti, na 1/10 polnogo oborota, a zatem skleivaetsya s protivopolozhnoi gran'yu. Hotya na risunke nekotorye planki pokazany snaruzhi dodekaedra, eto tol'ko "prizraki" (poskol'ku schitaetsya, chto vse prostranstvo sostoit lish' iz vnutrennih tochek dodekaedra). Kogda odna iz planok vydvigaetsya naruzhu, ee vystupayushaya chast' ischezaet, odnovremenno kak by vhodya vnutr' dodekaedra skvoz' protivopolozhnuyu gran'. Esli Vselennaya ustroena kak mnogoobrazie Zeiferta-Vebera, to ona konechna, no budet rasshiryat'sya vechno.

Ris. 2. Dvumernoe mnogoobrazie, nazyvaemoe dvumernym torom, mozhno predstavit' v vide kvadrata, protivopolozhnye storony kotorogo abstraktno skleeny drug s drugom: verhnyaya storona otozhdestvlena s nizhnei, a pravaya - s levoi. Esli razmechennaya planka vydvigaetsya naruzhu skvoz' pravuyu storonu, ona poyavlyaetsya snova s levoi storony; esli planka uhodit za verhnyuyu storonu, to ona poyavlyaetsya snizu. Vse vershiny kvadrata skleivayutsya v odnu tochku mnogoobraziya.

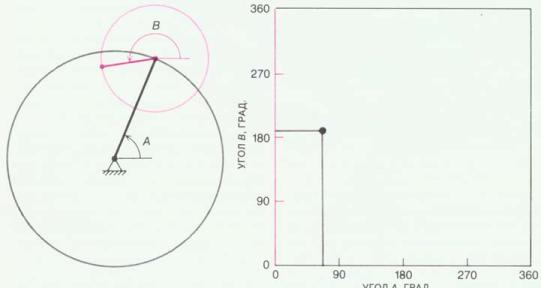
Ris. 3. Dvuzvennyi krivoship sostoit iz dvuh tverdyh sterzhnei, soedinennyh mezhdu soboi sharnirom; konec odnogo sterzhnya sharnirno zakreplen. Sterzhni mogut svobodno vrashat'sya vokrug sharnirov, ostavayas' v ploskosti izobrazheniya (sleva). Kazhdaya vozmozhnaya konfiguraciya dvuh sterzhnei mozhet byt' zadana tochkoi na ploskosti, na kotoroi vvedena pryamougol'naya sistema koordinat. Mnozhestvo vseh tochek etoi ploskosti, otvechayushih vsevozmozhnym konfiguraciyam sharnirnogo mehanizma, nazyvaetsya ego konfiguracionnym prostranstvom {sprava). Poskol'ku pri povorote lyubogo iz sterzhnei na 360o konfiguraciya mehanizma ne menyaetsya, ego konfiguracionnoe prostranstvo - eto kvadrat, storony kotorogo otvechayut znacheniyam 0 i 360o kazhdogo iz uglov. Sootvetstvuyushie tochki protivopolozhnyh storon kvadrata predstavlyayut odinakovye konfiguracii mehanizma, t.e. konfiguracionnoe prostranstvo^yavlyaetsya dvumernym torom.

Pervye sushestvennye prodvizheniya v topologicheskoi teorii 3-mnogoobrazii byli sdelany na rubezhe nashego veka v rabotah Anri Puankare, Maksa Dena i Paulya Hegora. Odna iz trudnostei pri izuchenii trehmernyh mnogoobrazii sostoit v tom, chto neposredstvenno-naglyadnye obrazy chastichno dolzhny ustupit' mesto abstraktnym predstavleniyam. Mnogie poverhnosti netrudno predstavit' sebe, poskol'ku na nih mozhno vzglyanut' snaruzhi, iz tret'ego izmereniya: razmernost' ob'emlyushego prostranstva na edinicu bol'she razmernosti poverhnosti. Dopolnitel'noe izmerenie ostavlyaet poverhnosti dostatochno svobody dlya izgibaniya i smykaniya s samoi soboi. Mozhno bylo by popytat'sya vzglyanut' i na trehmernye mnogoobraziya so storony, kak by iz chetvertogo izmereniya, no okazyvaetsya, chto v takih akrobaticheskih tryukah net neobhodimosti.

V XIX v. matematiki otkryli, chto lyuboe dvumernoe mnogoobrazie mozhno predstavit' kak mnogougol'nik, storony kotorogo opredelennym obrazom skleeny ili, inymi slovami, otozhdestvleny drug s drugom. V romane "Flatlandiya", opublikovannom v 1884 g., E.Ebbot opisyvaet dvumernoe sushestvo, postoyanno zhivushee na dvumernom mnogoobrazii s bolee ekzoticheskoi topologiei - na kvadrate, protivopolozhnye storony kotorogo otozhdestvleny. Kogda flatlandec peresekaet verhnyuyu storonu kvadrata, on vnov' poyavlyaetsya na nizhnei ego storone; esli on uhodit vpravo, to poyavlyaetsya sleva. Poetomu, po suti dela, verh kvadrata prikleen k ego nizu, a pravaya storona - k levoi. Stoit otmetit', chto tak zhe ustroeny mnogie videoigry: kogda figura uhodit za verhnii krai ekrana, ona poyavlyaetsya snizu, i t.d.

Dlya kvadrata skleivanie vypolnit' prosto. Soedinenie verhnei i nizhnei storon daet cilindr, otkrytyi s oboih torcov; skleivanie otkrytyh torcov daet bublik. Posle skleivaniya storon "shvy" ischezayut; flatlandec ne mozhet opredelit', gde bylo proizvedeno skleivanie. Bublik i kvadrat s nadlezhashim obrazom otozhdestvlennymi storonami schitayutsya topologicheski odnim i tem zhe abstraktnym mnogoobraziem, a imenno dvumernym torom.

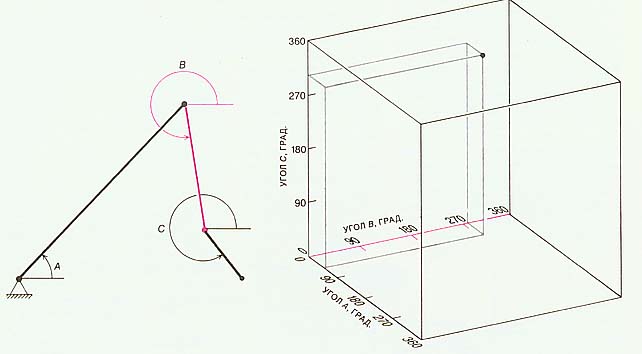
Ris. 4. Trehmernoe mnogoobrazie, analogichnoe dvumernomu toru, voznikaet kak konfiguracionnoe prostranstvo ploskogo trehzvennogo krivoshipa (sleva). Esli ugly, obrazovannye kazhdym sterzhnem s fiksirovannym napravleniem, otlozhit' na treh vzaimno perpendikulyarnyh osyah, to lyuboe vozmozhnoe polozhenie trehzvennogo krivoshipa mozhno izobrazit' tochkoi kuba (sprava). Pri polnom oborote kakogo-nibud' sterzhnya konfiguraciya mehanizma ne izmenyaetsya. Takim obrazom, v konfiguracionnom prostranstve kazhdaya gran' kuba, otvechayushaya povorotu sterzhnya na 360o, abstraktno otozhdestvlyaetsya s protivopolozhnoi gran'yu, otvechayushei povorotu togo zhe sterzhnya na nulevoi ugol. Poluchennoe trehmernoe mnogoobrazie nazyvaetsya trehmernym torom.

Odnako, kak pokazyvayut videoigry, dlya intuitivnogo ponimaniya dvumernogo tora ne obyazatel'no proizvodit' real'noe skleivanie. Nemnogo potrenirovavshis', mozhno s legkost'yu usledit' za dvizheniem ob'ekta po kvadratu, dlya kotorogo skleivanie tol'ko podrazumevaetsya. Abstraktnoe skleivanie vvodit v krug geometricheskoi intuicii mnogie mnogoobraziya, kotorye inache trudno bylo by sebe predstavit'. I vot chto dlya nas osobenno vazhno: tryuk so skleivaniem legko obobshaetsya i pozvolyaet dlya ponimaniya struktury 3-mnogoobrazii privlech' geometricheskuyu intuiciyu.

Rassmotrim trehmernoe mnogoobrazie, kotoroe porozhdaetsya pryamougol'nym blokom prostranstva, naprimer vnutrennei chast'yu komnaty. Skleim uslovno perednyuyu stenu komnaty s zadnei, levuyu stenu s pravoi, a potolok s polom. Esli by skleivanie bylo sdelano na samom dele, to prishlos' by voobrazit', chto komnata izgibaetsya i soedinyaetsya sama s soboi v chetvertom izmerenii. Odnako vse, chto nuzhno dlya opisaniya etogo mnogoobraziya, opredelyaetsya proceduroi abstraktnogo skleivaniya. Esli ob'ekt vnutri mnogoobraziya dvizhetsya k perednei stene, on ischezaet na nei i poyavlyaetsya na zadnei stene; tochno tak zhe, kogda ob'ekt ischezaet na pravoi stene, on poyavlyaetsya na levoi i ischezaet na potolke, kogda poyavlyaetsya na polu. Eto dvizhenie ochen' pohozhe na dvizhenie po dvumernomu toru; poluchennoe mnogoobrazie - trehmernyi analog dvumernogo tora i poetomu nazyvaetsya trehmernym torom.

Otvlekayas' ot obychnyh predstavlenii o prostranstve i fizicheskoi real'nosti, mozhno legko voobrazit' "zhizn'" v trehmernom tore. Esli smotret' na zadnyuyu stenu, to luch zreniya prohodit skvoz' etu stenu i vozvrashaetsya iz protivopolozhnoi tochki perednei steny; vy vidite svoyu kopiyu "anfas". Posmotrite vpravo - i uvidite svoyu kopiyu sleva, posmotrite vniz na pol - uvidite makushku svoei golovy. Poskol'ku luchi zreniya pri prodolzhenii peresekayut komnatu vo vseh napravleniyah mnozhestvo raz, vy vidite, chto voznikaet beskonechnoe chislo vashih kopii i kopii komnaty; vse oni raspolozheny v vide pryamougol'noi prostranstvennoi reshetki. Opticheskii effekt podoben tomu, kotoryi voznikaet v komnate, vse steny, pol i potolok kotoroi zerkal'ny. Raznica v tom, chto "otrazheniya" ne perevernuty, a v tochnosti povtoryayut original.

Astronomy ne obnaruzhili takih svoeobraznyh opticheskih effektov; sleduet li iz etogo, chto Vselennaya ne mozhet byt' trehmernym torom? Net. Vozrast Vselennoi nahoditsya primerno mezhdu 10 i 20 mlrd. let. Esli by ona byla trehmernym torom, naprimer, poryadka 60 mlrd. svetovyh let v poperechnike, to svet eshe ne uspel by sdelat' polnyi oborot. Drugaya vozmozhnost' sostoit v tom, chto nablyudatel'naya astronomiya uzhe zaregistrirovala svet, kotoryi prodelal polnyi put' vokrug Vselennoi: esli Vselennaya - trehmernyi tor, to odna iz dal'nih galaktik, kotorye my nablyudaem, mozhet byt' nashei sobstvennoi. Eto trudno bylo by proverit', poskol'ku izobrazhenie nashei Galaktiki sformirovano svetovymi luchami, pokinuvshimi istochniki sveta milliardy let nazad i potrativshimi eto vremya na peresechenie Vselennoi. Imeya neogranichennuyu razreshayushuyu sposobnost' zreniya, my mogli by uvidet' Mlechnyi Put' na rannih etapah ego evolyucii, v moment ispuskaniya sveta. Takaya Vselennaya imeet konechnyi ob'-em, no ne imeet nikakoi granicy.

Podobnye modeli vozmozhnoi prostranstvennoi struktury Vselennoi mozhno poluchit', pol'zuyas' vmesto kuba drugimi mnogogrannikami. Vo vseh sluchayah luchshii sposob ponyat' ustroistvo mnogoobraziya - eto voobrazit', chto opredelennye grani mnogogrannika abstraktno skleeny drug s drugom. Dva takih mnogoobraziya legko poluchit' iz pravil'nogo dodekaedra. 12 granei dodekaedra - pravil'nye pyatiugol'niki; ih mozhno razbit' na 6 par parallel'nyh mezhdu soboi diametral'no protivopolozhnyh granei. Pervoe trehmernoe dodekaedral'noe mnogoobrazie poluchaetsya tak: odin iz pyatiugol'nikov kazhdoi pary povorachivaetsya na 1/10 polnogo oborota protiv chasovoi strelki vokrug osi, perpendikulyarnoi ego ploskosti, posle chego otozhdestvlyaetsya so vtorym (protivopolozhnym emu) pyatiugol'nikom. Eto mnogoobrazie nazyvaetsya mnogoobraziem Puankare, potomu chto ono ekvivalentno trehmernomu mnogoobraziyu, otkrytomu Puankare v 1902 g. (Odnako Puankare ne znal, chto eto mnogoobrazie mozhno poluchit' iz dodekaedra.) Vtoroe dodekaedral'noe mnogoobrazie poluchaetsya skleivaniem kazhdogo pyatiugol'nika s protivopolozhnym, predvaritel'no povernutym na 3.10 polnogo oborota protiv chasovoi strelki vokrug osi, perpendikulyarnoi ego ploskosti. Eto mnogoobrazie nazyvaetsya dodekaedral'nym mnogoobraziem (ili prostranstvom) Zeiferta-Vebera v chest' G. Zeiferta i K. Vebera (rabotayushego seichas v Zhenevskom universitete); oni otkryli eto mnogoobrazie v 1932 g. (sm. Ris. 1.). Kak i trehmernyi tor, oba mnogoobraziya dayut modeli Vselennoi konechnogo ob'ema, no bez granicy ili kraya.

Podobnym obrazom mozhno poluchit' mnozhestvo razlichnyh modelei krupnomasshtabnoi struktury prostranstva. Poskol'ku bol'shinstvo mnogogrannikov nepravil'nye, bol'shinstvo trehmernyh mnogoobrazii prihoditsya skleivat' iz nih. Esli chislo granei veliko, to opisanie skleivaniya, kak pravilo, sil'no uslozhnyaetsya. Mozhet pokazat'sya, chto v takih zanyatiyah est' nechto nereal'noe. Nespecialist, veroyatno, soglasitsya, chto istinnaya topologiya prostranstva - dostoinyi ob'ekt dlya razmyshlenii; no ego, navernoe, udivilo by, kak daleko zavodyat eti razmyshleniya. V chastnosti, on mog by usomnit'sya v celesoobraznosti izucheniya "prostranstv" vo mnozhestvennom chisle. S tochki zreniya topologa, takaya kritika "b'et mimo celi," poskol'ku ona napravlena tol'ko na obrazno-opisatel'nuyu chast' topologii. Konechno, zanyatiya topologiei mozhno opravdat' ee primeneniyami k zadacham, voznikayushim v sovsem drugih situaciyah, no i sama po sebe topologiya - eto teoriya chistyh geometricheskih form, a ne teoriya real'nogo mira. Esli by zavtra struktura prostranstva kakim-nibud' obrazom stala izvestna, nikto iz topologov ne otkazalsya by ot izucheniya abstraktnyh prostranstv.

Ris. 5. Vid, otkryvayushiisya nablyudatelyu vnutri trehmernogo tora, pohozh na to, chto mozhno uvidet' v komnate, vse steny, pol i potolok kotoroi zerkal'ny; tol'ko izobrazhenie, v otlichie ot obychnogo zerkal'nogo otrazheniya, ne perevernuto. Luch zreniya uhodit, skazhem, skvoz' pravuyu stenu i vozvrashaetsya iz levoi steny; poetomu, glyadya napravo, nablyudatel' vidit komnatu tak, kak budto on smotrit na nee snaruzhi skvoz' prozrachnuyu levuyu stenu (tol'ko pri etom on vidit v komnate svoego dvoinika). Analogichnye kartiny voznikayut pri vzglyade vpered ili vverh. Tak kak luch zreniya pri prodolzhenii neogranichenno pronizyvaet trehmernyi tor, komnata budet vyglyadet' kak prostirayushayasya vo vse storony beskonechnaya pryamougol'naya reshetka. No trehmernyi tor ne beskonechen, poskol'ku vse vidimye obrazy, sostavlyayushie beskonechnuyu pryamougol'nuyu prostranstvennuyu reshetku, - izobrazheniya odnogo i togo zhe predmeta.

Eto utverzhdenie nikoim obrazom ne oznachaet, chto topologiya ne imeet otnosheniya k real'nomu miru. Naoborot, kak i drugie oblasti matematiki, topologiya imeet mnogochislennye prochnye svyazi s deistvitel'nost'yu, no eti svyazi ne pryamye. Esli nekotorye konkretnye obraznye predstavleniya (naprimer, prostranstvennye) stanovyatsya neubeditel'nymi, to luchshe otbrosit' eti predstavleniya, chem otkazat'sya ot izucheniya porozhdennyh imi matematicheskih ob'ektov. Opyt vnov' i vnov' pokazyvaet, chto matematicheskaya teoriya s bogatoi vnutrennei strukturoi obychno privodit k vyvodam, vazhnym dlya ponimaniya real'nogo mira, prichem chasto takimi putyami, kotorye nikak nel'zya bylo predvidet' do ee razvitiya. Nikakaya teoriya nikogda ne dostigla by toi stepeni zrelosti, na kotoroi tol'ko i voznikayut takie prilozheniya, esli by ona byla postoyanno obremenena uzhe otzhivshimi obraznymi predstavleniyami.

Chtoby ubedit'sya, naskol'ko shirok diapazon topologicheskih issledovanii, polezno na vremya pokinut' oblast' kosmologii i pereiti k bolee zemnym voprosam. Rassmotrim mehanicheskuyu sistemu (sharnirnyi mehanizm), sostoyashuyu iz sterzhnei i sharnirov, podobnuyu sisteme, kotoraya svyazyvaet mezhdu soboi klavishu i pechatayushii element v pishushei mashinke. My budem rassmatrivat' tol'ko ploskie sharnirnye mehanizmy, ili, inymi slovami, sistemy tverdyh sterzhnei, skreplennyh drug s drugom takim obrazom, chto vse sterzhni mogut dvigat'sya lish' v odnoi ploskosti. Pri etom hotya by v odnoi tochke sistema dolzhna byt' prikreplena k ploskosti; etu tochku nazovem bazovoi.

Zadacha teorii sharnirnyh mehanizmov - analiz vozmozhnyh ih dvizhenii. Sushestvuet mnogo real'nyh mehanicheskih ustroistv, k kotorym primenimo takoe issledovanie, prichem oni mogut i ne imet' vneshnego shodstva s sistemoi soedinennyh mezhdu soboi sterzhnei. Izuchenie sharnirnyh mehanizmov bylo ochen' populyarno vo vtoroi polovineXIX v., kogda interesovalis' zadachei postroeniya takih sharnirnyh mehanizmov, v kotoryh hotya by odna tochka dvigalas' po pryamoi linii. Kazalos', chto reshenie etoi zadachi moglo by imet' mnogo prakticheskih primenenii, naprimer pri konstruirovanii dvigatelei dlya parovozov. Odnako nesmotrya na to, chto bylo naideno mnogo elegantnyh teoreticheskih reshenii etoi zadachi, ni odno iz nih ne bylo primeneno na praktike.

Ris. 6. Poverhnost' bublika s odnoi dyrkoi mozhno razrezat' i razvernut' tak, chto poluchitsya kvadrat. Esli protivopolozhnye storony kvadrata abstraktno skleeny, to poluchennaya poverhnost' topologicheski ekvivalentna bubliku. Tak kak kvadrat ploskii, ego geometriya evklidova. Poetomu govoryat, chto s topologicheskoi tochki zreniya poverhnost' bublika s odnoi dyrkoi dopuskaet evklidovu geometriyu.

Sharnirnyi mehanizm matematicheski predstavlyaetsya sistemoi pryamolineinyh otrezkov na ploskosti; v nekotoryh tochkah peresecheniya otrezkov mogut byt' ustanovleny osi dlya sharnirov. V matematicheskoi teorii schitaetsya, chto otrezki i osi sharnirov mogut svobodno prohodit' drug skvoz' druga. Ne tak legko postroit' fizicheskuyu model', sterzhni i sharniry kotoroi povtoryayut dvizheniya ideal'nogo sharnirnogo mehanizma, no dlya matematicheskoi teorii eto nesushestvenno. Okazyvaetsya, chto dlya lyubogo "matematicheskogo" sharnirnogo mehanizma sushestvuet real'nyi mehanizm, vypolnyayushii te zhe dvizheniya; odnako sootvetstvuyushaya fizicheskaya sistema mozhet byt' ustroena znachitel'no slozhnee svoego teoreticheskogo ekvivalenta i vyglyadet' sovershenno inache.

Mnozhestvo vseh vozmozhnyh sostoyanii sharnirnogo mehanizma nazyvaetsya ego konfiguracionnym prostranstvom; v bol'shinstve sluchaev ono yavlyaetsya topologicheskim mnogoobraziem. Rassmotrim prosteishii sharnirnyi mehanizm, sostoyashii iz edinstvennogo sterzhnya, odin konec kotorogo shar-nirno zakreplen v bazovoi tochke ploskosti, a drugoi mozhet svobodno dvigat'sya v etoi ploskosti. Podvizhnyi konec sterzhnya opisyvaet okruzhnost' na ploskosti, i kazhdoi tochke etoi okruzhnosti sootvetstvuet edinstvennoe sostoyanie sistemy. Konfiguracionnoe prostranstvo est' okruzhnost', kotoruyu mozhno inache rassmatrivat' kak pryamolineinyi otrezok, koncy kotorogo abstraktno skleeny drug s drugom. Okruzhnost' yavlyaetsya odnomernym mnogoobraziem, analogichnym dvumernomu toru; kazhdaya tochka etogo mnogoobraziya otozhdestvlyaetsya s edinstvennym polozheniem rassmotrennogo sharnirnogo mehanizma.

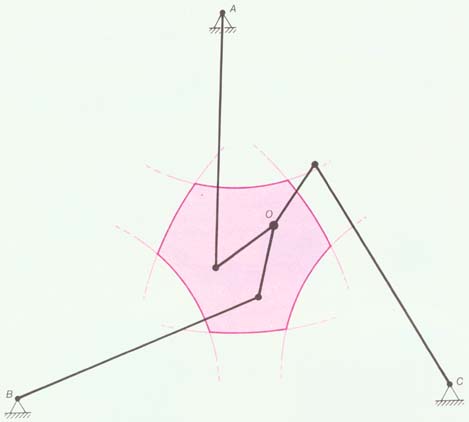
Ris. 7. Sharnirnomu mehanizmu, sostoyashemu iz treh dvuzvennyh krivoshipov, prisoedinennyh svobodnymi koncami k central'nomu sharniru, tozhe otvechaet dvumernoe konfiguracionnoe mnogoobrazie. Dvizhenie proishodit v ploskosti, i central'nyi sharnir mozhet nahodit'sya v lyuboi tochke krivolineinogo shestiugol'nika.

Prisoediniv drugoi sterzhen' k koncu pervogo, my poluchim dvuzvennyi krivoship - sharnirnyi mehanizm s dvumya stepenyami svobody. Eesli vtoroi sterzhen' koroche pervogo, to ego svobodnyi konec mozhet popast' v lyubuyu tochku kol'ca s centrom v bazovoi tochke. Eto kol'co snaruzhi ogranicheno okruzhnost'yu, radius kotoroi raven summe dlin oboih sterzhnei, a iznutri - okruzhnost'yu, radius kotoroi raven raznosti ih dlin. Esli sterzhni imeyut odinakovuyu dlinu, to svobodnyi konec vtorogo sterzhnya mozhet nahodit'sya v lyuboi tochke kruga, radius kotorogo raven summe dlin sterzhnei. Esli zhe vtoroi sterzhen' dlinnee pervogo, to vozmozhnye polozheniya ego svobodnogo konca snova zapolnyayut kol'co, vnutrennii radius kotorogo raven raznosti dlin sterzhnei. Odnako ne sleduet prinimat' eti mnozhestva tochek za konfiguracionnoe prostranstvo sharnirnogo mehanizma. Prichina razlichiya mezhdu nimi sostoit v tom, chto polozhenie konca vtorogo sterzhnya eshe ne polnost'yu opredelyaet konfiguraciyu sistemy. Dlya kazhdogo polozheniya svobodnogo konca vtorogo sterzhnya koleno nashego dvuzvennogo krivoshipa mozhet byt' vygnuto v tu ili druguyu storonu.

Chtoby pravil'no opisat' konfiguracionnoe prostranstvo, proshe rassmatrivat' vozmozhnye konfiguracii vsego dvoinogo krivoshipa, ne obrashaya vnimaniya na polozhenie ego svobodnogo konca. Kazhdaya konfiguraciya mozhet byt' zadana dvumya uglami, a imenno uglami mezhdu kazhdym iz sterzhnei i nekotorym fiksirovannym napravleniem (skazhem, napravleniem vpravo); ugly otschityvayutsya protiv chasovoi strelki. Eti dva ugla nezavisimo drug ot druga prinimayut vse znacheniya ot 0 do 360^o, no dlya kazhdogo sterzhnya ugly 0 i 360^o otozhdestvlyayutsya. Budem otkladyvat' eti ugly na vzaimno perpendikulyarnyh koordinatnyh osyah ploskosti; togda kazhdaya tochka kvadrata, ogranichennogo pryamymi liniyami, otvechayushimi znacheniyam 0 i 360^o kazhdogo iz uglov, izobrazhaet opredelennuyu konfiguraciyu dvoinogo krivoshipa. Krome togo, kazhdoi konfiguracii sistemy sootvetstvuet nekotoraya tochka etogo kvadrata. Poskol'ku ugly 0 i 360^o otozhdestvlyayutsya, verhnyaya storona kvadrata otozhdestvlyaetsya s nizhnei, a levaya - s pravoi. Itak, konfiguracionnoe prostranstvo yavlyaetsya dvumernym torom.

Esli prisoedinit' k svobodnomu koncu dvuzvennogo krivoshipa tretii sterzhen', to lyuboe polozhenie poluchennogo trehzvennogo krivoshipa mozhno opisat', zadav tri ugla, kotorye obrazuyut ego sterzhni s fiksirovannym napravleniem. Ugly snova otschityvayutsya protiv chasovoi strelki i probegayut znacheniya ot 0 do 360^o. Kak i prezhde, ugly 0 i 360^o otozhdestvlyayutsya. Esli velichiny treh uglov otlozhit' na treh vzaimno perpendikulyarnyh koordinatnyh osyah, to lyuboe vozmozhnoe polozhenie trehzvennogo krivoshipa budet predstavleno edinstvennoi tochkoi kuba, protivopolozhnye grani kotorogo abstraktno skleeny drug s drugom. Takim obrazom, konfiguracionnoe prostranstvo trehzvennogo krivoshipa ekvivalentno trehmernomu toru.

Vse rassmotrennye do sih por konfiguracionnye prostranstva svodilis' k mnogougol'nikam ili mnogogrannikam, storony ili grani kotoryh mozhno bylo skleit' bez iskazheniya ih razmerov i formy. No nikakie topologicheskie pravila ne zapreshayut skleivat' storony ili poverhnosti, geometricheski ne kongruentnye. To, chto v privedennyh nami primerah skleivanie chastei proishodilo bez iskazhenii, ob'yasnyaetsya lish' ves'ma chastnym harakterom etih primerov. Rassmotrim sharnirnyi mehanizm, sostoyashii iz treh dvuzvennyh krivoshipov; pust' kazhdyi iz nih sharnirno prikreplen k odnoi iz vershin ravnostoronnego treugol'nika, a vse svobodnye koncy skrepleny mezhdu soboi odnim central'nym sharnirom (sm. Ris. 8.). Dlya izucheniya konfiguracionnogo prostranstva etoi sistemy snachala postroim mnozhestvo vozmozhnyh polozhenii central'nogo sharnira. Svobodnyi konec kazhdogo dvuzvennogo krivoshipa dolzhen nahodit'sya v kol'ce s centrom v sootvetstvuyushei bazovoi tochke. Poetomu central'nyi sharnir mozhet popast' v lyubuyu tochku, lezhashuyu v peresechenii treh kolec, otvechayushih trem dvuzvennym krivoshipam. Eto peresechenie predstavlyaet soboi ploskii krivolineinyi shestiugol'nik.

Odnako dlya postroeniya konfiguracionnogo prostranstva eshe ne dostatochno etogo shestiugol'nika. Vspomnim, chto kazhdomu polozheniyu svobodnogo konca dvuzvennogo krivoshipa otvechayut dve razlichnye konfiguracii. Tochno tak zhe dlya lyuboi tochki shestiugol'nika koleno kazhdogo iz treh dvuzvennyh krivoshipov mozhet byt' vygnuto v odnu iz dvuh storon. Tem samym obshee chislo konfiguracii sistemy treh dvuzvennyh krivoshipov pri fiksirovannom vnutri shestiugol'nika polozhenii central'nogo sharnira ravno 23, t. e. 8. Poetomu konfiguracionnoe prostranstvo opisannoi sistemy mozhet byt' postroeno iz vos'mi krivolineinyh shestiugol'nikov s pomosh'yu podhodyashego abstraktnogo skleivaniya ih storon.

Kak zhe dolzhny byt' skleeny eti vosem' shestiugol'nikov, chtoby poluchilos' konfiguracionnoe prostranstvo? Esli central'nyi sharnir sistemy treh dvuzvennyh krivoshipov nahoditsya na storone ploskogo shestiugol'nika, to oba sterzhnya odnogo iz etih krivoshipov nepremenno dolzhny lech' na odnu pryamuyu. Takoe vypryamlenie mozhet proizoiti dvumya sposobami: sterzhni dvuzvennogo krivoshipa mogut byt' napravleny libo odinakovo, libo protivopolozhno. Odnako v oboih sluchayah konfiguraciya vsego sharnirnogo mehanizma odnoznachno opredelena, kak tol'ko zadany polozhenie central'nogo sharnira i napravleniya, v kotoryh vygnuty kolena dvuh drugih dvuzvennyh krivoshipov. Kazhdoi ih teh dvuh storon ploskogo shestiugol'nika, po kotorym mozhet dvigat'sya central'nyi sharnir, kogda pervyi dvuzvennyi krivoship vypryamlen, v konfiguracionnom prostranstve otvechaet ne 8, a lish' 22 = 4 razlichnyh reber. Vdol' kazhdogo takogo rebra v konfiguracionnom prostranstve skleivayutsya dva shestiugol'nika. Eti dva shestiugol'nika otvechayut dvum razlichnym napravleniyam vygiba kolena dvuzvennogo krivoshipa. Protivopolozhnaya storona pervogo shestiugol'nika v konfiguracionnom prostranstve takzhe skleivaetsya s protivopolozhnoi storonoi vtorogo shestiugol'nika, ibo pri raspolozhenii na nei central'nogo sharnira pervyi dvuzvennyi krivoship tozhe vypryamlyaetsya. Napravleniya vygiba dvuh drugih dvuzvennyh krivoshipov ne menyayutsya pri perehode ot pervogo ko vtoromu shestiugol'niku. Tochno takie zhe rassuzhdeniya primenimy ko vsem drugim rebram konfiguracionnogo prostranstva.

Esli central'nyi sharnir nashego mehanizma nahoditsya v vershine ploskogo shestiugol'nika, to dva iz dvuzvennyh krivoshipov dolzhny vypryamit'sya. Poetomu v konfiguracionnom prostranstve kazhdoi vershine ploskogo shestiugol'nika sootvetstvuyut dve tochki vmesto vos'mi - po odnoi na kazhdyi iz dvuh sposobov izgiba tret'ego dvuzvennogo krivoshipa. Chetyre abstraktnyh shestiugol'nika, otvechayushie chetyrem sposobam, kotorymi mogut vygnut'sya dva dvuzvennyh krivoshipa pri sdvige central'nogo sharnira iz vershiny vnutr' ploskogo shestiugol'nika, imeyut v konfiguracionnom prostranstve obshuyu vershinu.

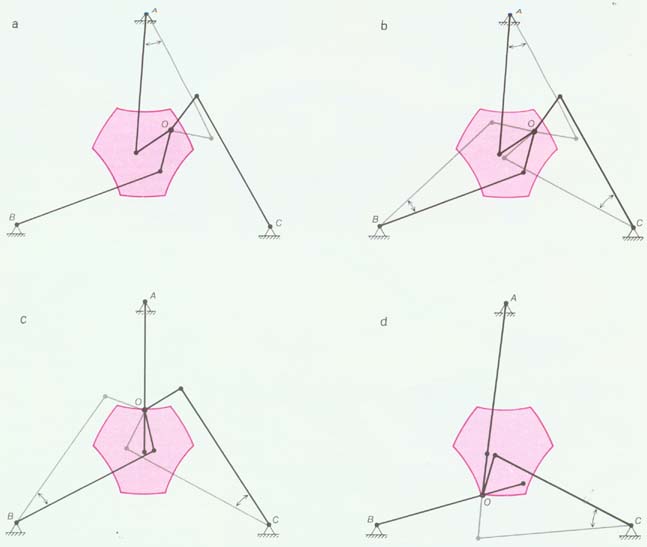
Ris. 8. Konfiguracionnoe prostranstvo sharnirnogo mehanizma, sostoyashego iz treh dvuzvennyh krivoshipov, - eto dvumernoe mnogoobrazie, razlichnye tochki kotorogo otvechayut raznym konfiguraciyam (t.e. vsevozmozhnym polozheniyam) etogo mehanizma. Pri fiksirovannom vnutri ploskogo krivolineinogo shestiugol'nika polozhenii central'nogo sharnira kazhdyi iz dvuzvennyh krivoshipov mozhet byt' vygnut odnim iz dvuh vozmozhnyh sposobov (a). Napravlenie vygiba kazhdogo dvuzvennogo krivoshipa ne zavisit ot togo, v kakuyu storonu vygnuty dva drugih; poetomu kazhdoi vnutrennei tochke shestiugol'nika sootvetstvuet 23 = 8 razlichnyh konfiguracii vsego mehanizma ('). Esli central'nyi sharnir nahoditsya na storone shestiugol'nika, to tol'ko dva iz dvuzvennyh krivoshipov mogut menyat' napravlenie vygiba; etomu sluchayu otvechayut lish' chetyre konfiguracii mehanizma (s). Esli central'nyi sharnir nahoditsya v vershine shestiugol'nika, to tol'ko odin iz dvuzvennyh krivoshipov mozhet menyat' napravlenie vygiba; takomu polozheniyu central'nogo sharnira otvechayut lish' dve konfiguracii mehanizma (d).

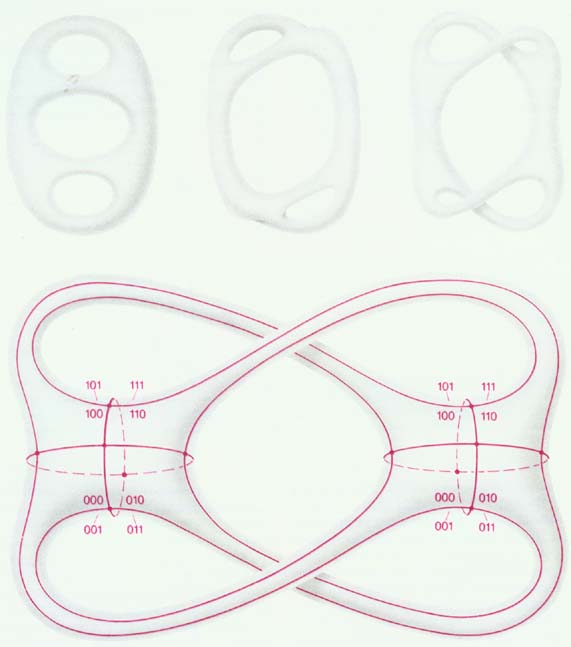
Ris. 9. Vosem' abstraktnyh shestiugol'nikov pri skleivanii obrazuyut konfiguracionnoe prostranstvo sharnirnogo mehanizma, sostoyashego iz treh dvuzvennyh krivoshipov. Kazhdyi shestiugol'nik otvechaet odnomu iz vos'mi sposobov raspolozheniya treh dvuzvennyh krivoshipov pri fiksirovannom vnutri ploskogo krivolineinogo shestiugol'nika polozhenii central'nogo sharnira. Polozhenie, v kotorom koleno dvuzvennogo krivoshipa lezhit sprava ot otrezka, soedinyayushego nachalo pervogo sterzhnya s koncom vtorogo, pomecheno cifroi 0; protivopolozhnoe polozhenie kolena pomecheno cifroi 1. Abstraktnye shestiugol'niki okazyvayutsya pomechennymi trehznachnymi dvoichnymi chislami. Chtoby bolee naglyadno pokazat' primykanie etih shestiugol'nikov drug k drugu v konfiguracionnom prostranstve, mozhno raspolozhit' ih na poverhnosti krendelya s tremya dyrkami, deformiruya ih tak, kak budto oni sdelany iz reziny. Dlya bol'shei simmetrii kartiny poverhnost' krendelya s tremya dyrkami predvaritel'no preobrazuetsya v topologicheski ekvivalentnoe ei mnogoobrazie, izobrazhennoe v nizhnei chasti risunka. Trehznachnye dvoichnye chisla, kotorymi pomecheny shestiugol'niki, ukazyvayut sposob skleivaniya. Esli dvoichnye metki dvuh shestiugol'nikov sovpadayut v dvuh iz treh razryadov, to takie shestiugol'niki skleivayutsya vdol' dvuh protivopolozhnyh storon. Eti storony opredelyayutsya temi dvumya storonami ploskogo krivolineinogo shestiugol'nika, kotorym otvechaet vypryamlenie dvuzvennogo krivoshipa s tem zhe nomerom, chto i nomer sovpadayushego dvoichnogo razryada. Kazhdye chetyre shestiugol'nika, metki kotoryh sovpadayut v odnom razryade, v konfiguracionnom prostranstve imeyut obshuyu vershinu. Diametral'no protivopolozhnye vershiny etih chetyreh shestiugol'nikov soedinyayutsya v drugoi tochke konfiguracionnogo prostranstva. Eti dve tochki izobrazhayut konfiguracii, v kotoryh vypryamleny dva dvuzvennyh krivoshipa s nomerami, otvechayushimi nomeram dvuh par nesovpadayushih dvoichnyh razryadov.

Konfiguracionnoe prostranstvo yavlyaetsya poverhnost'yu, kotoraya v otlichie ot ploskogo shestiugol'nika ne imeet ni uglov, ni granicy. Etu poverhnost' mozhno razbit' na vosem' shestiugol'nikov. Pri etom poluchayutsya 6 h 22 = 24 rebra, po kotorym chasti primykayut drug k drugu, i 6 h 2 = 12 vershin, v kotoryh shodyatsya po chetyre chasti.

Opisanie konfiguracionnogo prostranstva sistemy treh dvuzvennyh krivoshipov, kotoroe my priveli vyshe, logicheski polno, poskol'ku opredeleny vse abstraktnye otozhdestvleniya. Tem ne menee gorazdo udobnee proizvesti real'nye skleivaniya i postroit' poluchennoe mnogoobrazie kak zamknutuyu poverhnost' v prostranstve. Okazyvaetsya, takoe postroenie vsegda osushestvimo, esli abstraktnoe skleivanie privodit k mnogoobraziyu, udovletvoryayushemu odnomu tehnicheskomu usloviyu, nazyvaemomu orientiruemost'yu. Mnogoobrazie, kotoroe my opisali vyshe, orientiruemo; poetomu skleivanie mozhno proizvesti, no eto ne tak prosto.

V seredine XIX v. bylo dokazano, chto lyuboe orientiruemoe dvumernoe mnogoobrazie topologicheski ekvivalentno poverhnosti krendelya s nekotorym chislom dyrok. [Prim. perev. Takuyu poverhnost' nazyvayut takzhe sferoi s ruchkami (ili dyrkami).] Chislo dyrok nazyvaetsya rodom poverhnosti. Naprimer, poverhnost' sfery imeet rod 0. Rod poverhnosti kofeinoi chashki s ruchkoi, tak zhe kak i poverhnosti bublika, raven 1. Rod poverhnosti krendelya zavisit ot masterstva konditera.

Dlya lyuboi poverhnosti, razbitoi na mnogougol'nye kletki proizvol'noi formy, chislo etih kletok minus chislo reber plyus chislo vershin est' konstanta, zavisyashaya tol'ko ot poverhnosti. Zamechatel'no, chto eta konstanta ne zavisit ot sposoba razbieniya poverhnosti na mnogougol'nye kletki; ona nazyvaetsya eilerovoi harakteristikoi poverhnosti v chest' velikogo matematika Leonarda Eilera. Eilerova harakteristika poverhnosti roda n ravna 2-2n. Tak kak poverhnost' mozhet byt' iskrivlena v prostranstve, to mnogougol'niki ne obyazany byt' ploskimi, a ih storony mogut byt' pochti proizvol'nymi krivymi. Naprimer, sferu mozhno razbit' na vosem' treugol'nikov, soediniv severnyi i yuzhnyi polyusy s chetyr'mya tochkami na ekvatore. Tak kak v sfere net dyrok, to ee rod raven 0, a eilerova harakteristika dolzhna ravnyat'sya 2-2h0, t.e. 2. Legko proverit', chto pri nashem razbienii na poverhnosti sfery 6 vershin i 12 reber, tak chto eilerova harakteristika sfery, razbitoi na 8 treugol'nikov, i v samom dele ravna 2. Stoit otmetit', chto kolichestva granei, reber i vershin v etom primere otvechayut pravil'nomu oktaedru, topologicheski ekvivalentnomu sfere.

Ris. 10. Geometriya sfery, nazyvaemaya ellipticheskoi, otlichaetsya ot obychnoi evklidovoi geometrii ploskosti. Tak, summa vnutrennih uglov sfericheskogo treugol'nika uzhe ne ravna 180o i uvelichivaetsya pri uvelichenii ego ploshadi {sleva). Otrezannaya ot sfery kruglaya "shapochka" pri rasplastyvanii tresnula by i razorvalas', kak pokazano sprava. Ploshad' kruga na sfere men'she ploshadi ploskogo kruga togo zhe radiusa. Sfera imeet postoyannuyu polozhitel'nuyu kriviznu.

Ris. 11. Geometriya poverhnosti postoyannoi otricatel'noi krivizny (sleva) nazyvaetsya giperbolicheskoi. Summa vnutrennih uglov treugol'nika na takoi poverhnosti men'she 180o i umen'shaetsya pri uvelichenii ploshadi treugol'nika. Krug, vyrezannyi iz giperbolicheskoi poverhnosti, pri rasplastyvanii budet smorshivat'sya i nakladyvat'sya sam na sebya, kak pokazano sprava. Ego ploshad' bol'she ploshadi ploskogo kruga togo zhe radiusa. Bumazhnuyu model' giperbolicheskoi poverhnosti mozhno skleit' iz neskol'kih ravnostoronnih treugol'nikov tak, chtoby v kazhdoi vershine shodilis' sem' treugol'nikov.

Ris. 12. Ugly pravil'nogo shestiugol'nika mozhno umen'shit', "rastyagivaya" ego na giperbolicheskoi poverhnosti. Na risunke shestiugol'nik rastyanut do polozheniya, v kotorom vse ugly stanovyatsya pryamymi. Vosem' shestiugol'nikov v konfiguracionnom prostranstve sistemy treh dvuzvennyh krivoshipov skleivayutsya po chetyre v odnoi vershine, poetomu vse ih vnutrennie ugly dolzhny byt' pryamymi. Esli kazhdyi iz etih shestiugol'nikov deformirovat' v giperbolicheskii shestiugol'nik s pryamymi uglami i, kak i ran'she, abstraktno skleit', to poluchennoe dvumernoe mnogoobrazie budet imet' postoyannuyu otricatel'nuyu kriviznu. Govoryat, chto ego geometriya lokal'no-odnorodna. Etot priem znachitel'no uproshaet geometriyu konfiguracionnogo prostranstva.

Tak kak konfiguracionnoe prostranstvo sistemy treh dvuzvennyh krivoshipov mozhno razbit' na 8 shestiugol'nyh granei s 24 rebrami i 12 vershinami, eilerova harakteristika etogo prostranstva ravna 8 - 24 + 12 = -4. Rod n etogo mnogoobraziya mozhno vychislit', priravnivaya vyrazhenie 2-2n dlya eilerovoi harakteristiki naidennomu ee znacheniyu -4. Otsyuda sleduet, chto n=3. Itak, vosem' shestiugol'nikov konfiguracionnogo prostranstva rassmotrennogo sharnirnogo mehanizma mozhno s soblyudeniem pravil skleiki raspolozhit' na poverhnosti krendelya s tremya dyrkami (sm. Ris. 9.).

Naglyadnoe izobrazhenie mnogoobraziya vrode krendelya s tremya dyrkami udobno blagodarya svoei konkretnosti, no u nego est' i ryad nedostatkov. Naprimer, izobrazhaya eto mnogoobrazie v obychnom prostranstve, prihoditsya otkazat'sya ot mnogih simmetrii, prisushih ego abstraktnomu opisaniyu. V pervonachal'nom opisanii konfiguracionnogo prostranstva sistemy treh dvuzvennyh krivoshipov kazhdyi shestiugol'nik kongruenten lyubomu drugomu. Krome togo, povorot lyubogo shestiugol'nika na ugol 120 i 240^o ostavlyaet ego neizmennym. Odnako pri naglyadnom izobrazhenii konfiguracionnogo prostranstva bol'shaya chast' simmetrii teryaetsya. Shestiugol'niki na krendele s tremya dyrkami ne kongruentny i ne imeyut vrashatel'noi simmetrii: povoroty lyubogo iz nih na 120 i 240^o nel'zya sdelat' bez izmeneniya ego formy.

Drugoe "neudobstvo" krendelya s tremya dyrkami vyzvano izmeneniem geometricheskih svoistv ego poverhnosti ot tochki k tochke: svoistva poverhnosti na vneshnem obvode otlichayutsya ot ee svoistv vblizi odnoi iz dyrok. Sleduet podcherknut', chto geometricheskie svoistva, o kotoryh my govorim, yavlyayutsya "vnutrennimi" dlya etoi poverhnosti. Vnutrennyaya geometriya poverhnosti opredelyaetsya rezul'tatami teh izmerenii, kotorye mozhno provesti na nei samoi, ne obrashayas' k okruzhayushemu ee prostranstvu. Etu geometriyu sleduet otlichat' ot vneshnei geometrii poverhnosti, kotoraya opisyvaet, kakim obrazom poverhnost' vlozhena v prostranstvo. Naprimer, vnutrennyaya geometriya cilindra ili konusa, poluchennogo izgibaniem ploskogo lista bumagi, ta zhe, chto i u etogo ploskogo lista, hotya ih vneshnie geometrii sovershenno razlichny.

Poetomu tot fakt, chto so storony poverhnost' vyglyadit neravnomerno iskrivlennoi, ne yavlyaetsya nadezhnym pokazatelem togo, chto eto svoistvo ee vnutrennei geometrii. V chem zaklyuchaetsya vnutrennee otlichie naruzhnyh uchastkov poverhnosti krendelya ot uchastkov vblizi dyrok? Voobrazim, chto iz naruzhnoi vypukloi chasti krendelya vyrezan malen'kii kusochek i rasplastan na stole. Pri etom on razorvetsya podobno apel'sinovoi korke. Obratnyi process chasto praktikuetsya portnym pri izgotovlenii detalei odezhdy, kotorye dolzhny prinimat' vypukluyu formu (naprimer, lif plat'ya). Iz tkani udalyaetsya klin, nazyvaemyi vytachkoi, i kraya vyreza sshivayutsya drug s drugom.

Odnako, esli malen'kii kusochek vyrezan iz poverhnosti krendelya vblizi dyrki, to pri popytke raspryamit' ego na stole on smorshivaetsya i nakladyvaetsya sam na sebya. Portnoi mozhet obratit' etot process, delaya prodol'nyi razrez v tkani i vshivaya v nego dopolnitel'nyi klin. Eta konstrukciya ispol'zuetsya dlya izgotovleniya yubki, uzkoi vverhu i raskleshennoi vnizu. Budet li gotovaya detal' odezhdy na ploskoi poverhnosti razryvat'sya, skladyvat'sya ili plotno primykat' k poverhnosti - eto vazhnaya harakteristika ee vnutrennei geometrii.

Vnutrennyaya geometriya poverhnosti bublika s odnoi dyrkoi menyaetsya ot tochki k tochke tak zhe, kak u krendelya s tremya dyrkami. Pri etom, kak my uzhe podcherkivali, bublik s odnoi dyrkoi i kvadrat, protivopolozhnye storony kotorogo otozhdestvleny, imeyut odnu i tu zhe topologiyu. Odnako vnutrennyaya geometriya kvadrata znachitel'no proshe, chem u bublika s odnoi dyrkoi: v maloi okrestnosti lyuboi tochki kvadrata ona sovpadaet s vnutrennei geometriei kusochka ploskosti. Eto svoistvo verno dazhe dlya tochek na storonah i v vershinah kvadrata. Inache govorya, dlya kvadrata s otozhdestvlennymi protivopolozhnymi storonami vnutrennyaya geometriya lyuboi maloi oblasti na nem odinakova. Vnutrennyaya geometriya, obladayushaya takogo tipa ravnomernost'yu, nazyvaetsya lokal'no-odnorodnoi.

Vvedenie ponyatiya lokal'noi odnorodnosti imelo bol'shoe znachenie dlya izucheniya dvumernyh mnogoobrazii. Okolo sta let nazad bylo dokazano, chto lyubuyu poverhnost', a ne tol'ko bublik s odnoi dyrkoi, mozhno realizovat' takim obrazom, chto ee geometriya budet lokal'no-odnorodnoi. Krome togo, na kazhdoi poverhnosti mozhet sushestvovat' lish' odin tip lokal'no-odnorodnoi geometrii.

Dlya poverhnostei sushestvuet tol'ko tri tipa lokal'no-odnorodnyh vnutrennih geometrii. Pervyi tip - eto prosto evklidova geometriya ploskosti. Dlina okruzhnosti na ploskosti ravna diametru, umnozhennomu na zh, a summa vnutrennih uglov treugol'nika sostavlyaet 180^o. Govoryat, chto ploskost' imeet nulevuyu gaussovu kriviznu. Gaussova krivizna, vpervye vvedennaya Karlom Fridrihom Gaussom, predstavlyaet soboi chislovuyu harakteristiku vnutrennei formy poverhnosti.

Vtoroi tip lokal'no-odnorodnoi vnutrennei geometrii - eto geometriya poverhnosti sfery. Otrezannaya ot sfery kruglaya "shapochka" pri rasplastyvanii na ploskosti razryvaetsya tochno tak zhe, kak vypuklyi kusochek krendelya. Znachit, dlina okruzhnosti kruga na sfere men'she dliny okruzhnosti ploskogo kruga, imeyushego takoi zhe radius. Etot "defekt" dliny granicy kruga na sfere ob'yasnyaet proishozhdenie standartnogo nazvaniya lokal'no-odnorodnoi geometrii sfery: ellipticheskaya geometriya (ot grecheskogo slova - nedostatok, iz'yan). Summa vnutrennih uglov treugol'nika, postroennogo na sfere, prevyshaet 180^o; eta summa tem bol'she, chem bol'she otnoshenie ploshadi treugol'nika k ploshadi poverhnosti sfery (sm. Ris. 10). Sfera imeet postoyannuyu polozhitel'nuyu gaussovu kriviznu.

Kak i sledovalo ozhidat', kruzhok, vyrezannyi iz poverhnosti s lokal'no-odnorodnoi geometriei tret'ego tipa, pri rasplastyvanii na ploskosti chastichno nalegaet sam na sebya podobno blizkomu k dyrke kusochku poverhnosti krendelya. Dlina okruzhnosti takogo kruzhka bol'she dliny okruzhnosti sootvetstvuyushego kruga na ploskosti. Poetomu eta geometriya nazyvaetsya giperbolicheskoi (ot grecheskogo slova - prevoshodstvo, izbytok). Nevozmozhno zadat' vsyu giperbolicheskuyu poverhnost' kakoi-nibud' odnoi analiticheskoi formuloi, no mozhno priblizhenno smodelirovat' bol'shie ee kuski (sm. Ris. 11). Summa vnutrennih uglov treugol'nika na takoi poverhnosti men'she 180^o; chem bol'she ploshad' treugol'nika, tem men'she summa ego vnutrennih uglov. Giperbolicheskaya poverhnost' imeet postoyannuyu otricatel'nuyu gaussovu kriviznu.

Interesno pokazat', kak mozhno zadat' lokal'no-odnorodnuyu geometriyu na krendele s tremya dyrkami. Vspomnim, chto shestiugol'niki, iz kotoryh pervonachal'no bylo postroeno mnogoobrazie, mozhno izgibat' i deformirovat' lyubym sposobom, lish' by ne bylo razrezov ili razryvov. Metod sostoit v sleduyushem: kazhdyi shestiugol'nik deformiruyut tak, chtoby on imel lokal'no-odnorodnuyu geometriyu, no po-prezhnemu primykal k drugim shestiugol'nym kuskam mnogoobraziya, kak na krendele s tremya dyrkami.

Ris. 13. Mnogoobrazie zeiferta-vebera mozhno nadelit' lokal'no-giperbolicheskoi geometriei, esli porozhdayushemu ego dodekaedru pozvolit' "rasti" v giperbolicheskom prostranstve. Rost mnogogrannika v giperbolicheskom prostranstve podoben rastyagivaniyu mnogougol'nika na giperbolicheskoi poverhnosti. Kogda dodekaedr uvelichivaetsya, telesnye ugly pri ego vershinah umen'shayutsya i kazhdaya vershina stanovitsya vse ostree. Pri abstraktnom skleivanii, dayushem mnogoobrazie Zeiferta-Vebera, vse 20 vershin dodekaedra dolzhny soitis' v odnoi tochke. Poetomu telesnye ugly pri vershinah nuzhno umen'shit' v giperbolicheskom prostranstve do takih razmerov, chtoby 20 takih uglov mozhno bylo plotno somknut' v odnoi tochke.

Ris. 14. Dodekaedral'noe prostranstvo Puankare tozhe poluchaetsya iz dodekaedra skleivaniem par protivopolozhnyh granei, tol'ko pri etom skleivanii odna iz dvuh granei povorachivaetsya na 1/10 polnogo oborota, a ne na 3/10, kak pri postroenii mnogoobraziya Zeiferta-Vebera. Abstraktnoe skleivanie privodit k tomu, chto v odnoi tochke prostranstva shodyatsya chetyre vershiny dodekaedra. Telesnyi ugol pri vershine obychnogo dodekaedra neskol'ko mal dlya togo, chtoby chetyre takih ugla mozhno bylo plotno somknut' v odnoi tochke. No eti ugly mozhno uvelichit', "razduvaya" dodekaedr v ellipticheskom prostranstve. Etot effekt protivopolozhen tomu, chto proishodit pri razduvanii mnogogrannika v giperbolicheskom prostranstve.

My znaem, chto na krendele s tremya dyrkami v kazhdoi vershine shodyatsya chetyre iz vos'mi shestiugol'nikov. Esli by eto byli evklidovy shestiugol'niki, to summa uglov pri kazhdoi vershine ravnyalas' by 180^o, chto nevozmozhno. Esli by geometriya shestiugol'nikov byla sfericheskoi, to summa uglov pri vershine stala by eshe bol'she, chto tozhe nevozmozhno. Odnako na giperbolicheskoi ploskosti chem bol'she mnogougol'nik, tem men'she ego vnutrennie ugly. Dostatochno bol'shoi shestiugol'nik na giperbolicheskoi ploskosti dolzhen imet' vnutrennie ugly 90^o, i chetyre takih shestiugol'nika plotno prilegayut drug k drugu v vershine. Sledovatel'no, esli vosem' shestiugol'nikov, raspolozhennyh na giperbolicheskoi ploskosti, rastyagivat' na nei do teh por, poka ih vnutrennie ugly ne dostignut 90^o, to skleennoe iz nih mnogoobrazie budet imet' lokal'no-odnorodnuyu giperbolicheskuyu geometriyu. V etoi novoi forme mnogoobrazie uzhe trudnee naglyadno predstavit', no ego geometricheskie svoistva gorazdo proshe.

Chitatel' mozhet dostavit' sebe udovol'stvie i proverit', chto poverhnost' lyubogo krendelya s dvumya ili bolee dyrkami mozhno razrezat' na shestiugol'niki, shodyashiesya po chetyre v kazhdoi vershine. Esli stroit' takoe mnogoobrazie iz giperbolicheskih shestiugol'nikov s podhodyashimi vnutrennimi uglami, to na nem mozhno vvesti giperbolicheskuyu geometriyu. Bolee tradicionnyi sposob sostoit v razrezanii poverhnosti vdol' neskol'kih krivyh ("razrezov"), ishodyashih iz odnoi tochki, tak chto v itoge ona polnost'yu "raskryvaetsya" i poluchaetsya mnogougol'nik, vse vershiny kotorogo na poverhnosti skleeny v odnu tochku. Naprimer, poverhnost' krendelya s tremya dyrkami mozhno takim razrezaniem prevratit' v dvenadcatiugol'nik (ili v vosem' shestiugol'nikov). Mnogougol'nik, poluchennyi razrezaniem dostatochno slozhnoi poverhnosti, dolzhen imet' po krainei mere shest' storon. Esli vse vnutrennie ugly takogo mnogougol'nika ravny, to oni dolzhny byt' men'she, chem u sootvetstvuyushego pravil'nogo mnogougol'nika na evklidovoi ploskosti. Eto umen'shenie uglov dostigaetsya rastyazheniem mnogougol'nika na giperbolicheskoi ploskosti. Pri poparnom skleivanii storon mnogougol'nika poluchaetsya poverhnost', topologicheski identichnaya prezhnei, no imeyushaya lokal'no-odnorodnuyu geometriyu, "unasledovannuyu" ot giperbolicheskoi ploskosti.

Ris. 15. Sharovoi "lomtik" iskrivlennogo trehmernogo mnogoobraziya, analogichnyi krugovym "srezam", pokazannym na risunkah 10 i 11, nel'zya bez iskazheniya pomestit' v trehmernoe evklidovo prostranstvo. Trehmernoe mnogoobrazie postoyannoi polozhitel'noi krivizny pri takoi popytke "razorvalos'" by so vseh storon (a); kazhdoe dvumernoe sechenie etogo mnogoobraziya imeet kriviznu, kak u obychnoi sfery (b). Analogichno kazhdoe dvumernoe sechenie trehmernogo mnogoobraziya postoyannoi otricatel'noi krivizny smorshilos' by i nalozhilos' samo na sebya, kak kusok giperbolicheskoi poverhnosti (s). Trehmernoe mnogoobrazie, krivizna kotorogo v razlichnyh dvumernyh napravleniyah razlichna, vse zhe mozhet imet' lokal'no-odnorodnuyu geometriyu; tak budet v tom sluchae, kogda vo vseh tochkah mnogoobraziya zavisimost' krivizny ot napravleniya odinakova. Naprimer, odno dvumernoe sechenie takogo mnogoobraziya pri rasplastyvanii mozhet smorshivat'sya i nakladyvat'sya samo na sebya, a secheniya v dvuh drugih dvumernyh napravleniyah mogut razryvat'sya na chasti (d).

Sushestvuyut tol'ko chetyre zamknutye poverhnosti, lokal'no-odnorodnaya geometriya kotoryh ne giperbolicheskaya; poluchennye pri razrezanii etih poverhnostei mnogougol'niki imeyut men'she shesti storon. Iz bublika s odnoi dyrkoi poluchaetsya kvadrat, i vse chetyre ugla kvadrata mogut byt' skleeny bez izmeneniya ih velichin. A raz net neobhodimosti v deformacii, to voznikayushaya lokal'no-odnorodnaya geometriya na dvumernom tore - evklidova. Analogichnym obrazom sfera i neorientiruemoe dvumernoe mnogoobrazie, nazyvaemoe proektivnoi ploskost'yu, snabzhaetsya ellipticheskoi geometriei, a na neori-entiruemom mnogoobrazii, nazyvaemom butylkoi Kleina, zadaetsya evklidova geometriya.

Trehmernoe mnogoobrazie mozhet iskrivlyat'sya primerno tak zhe, kak i poverhnost': esli trehmernoe mnogoobrazie imeet polozhitel'nuyu kriviznu, to lyuboi ego dvumernyi srez pri rasplastyvanii na obychnoi evklidovoi ploskosti razorvetsya; esli zhe krivizna trehmernogo mnogoobraziya otricatel'na, to pri takoi procedure lyuboi ego dvumernyi srez smorshitsya i chastichno nalozhitsya sam na sebya. Ellipticheskaya, giperbolicheskaya i evklidova geometrii poverhnostei imeyut sootvetstvuyushie trehmernye analogi.

V 1976 g. odin iz nas (Terston) prishel k mysli, chto pri pomoshi lokal'no-odnorodnoi giperbolicheskoi geometrii udastsya ponyat' strukturu bol'shinstva trehmernyh mnogoobrazii. Eto yavilos' syurprizom dlya mnogih topologov, poskol'ku trehmernye mnogoobraziya ustroeny gorazdo slozhnee, chem dvumernye. V to vremya kak orientiruemye dvumernye mnogoobraziya mozhno perechislit', poskol'ku oni polnost'yu harakterizuyutsya svoim rodom, kazhdoe trehmernoe mnogoobrazie, podobno pereputannoi verevochnoi petle, imeet, kazalos' by, svoi sobstvennye, lish' emu prisushie svoistva i ne podhodit ni pod kakuyu shemu klassifikacii. Odnako pri bolee tshatel'nom izuchenii takaya shema vse zhe obnaruzhivaetsya. Osnovoi dlya etogo sluzhit to obstoyatel'stvo, chto na mnogih trehmernyh mnogoobraziyah mozhno zadat' lokal'no-odnorodnuyu geometriyu.

Kak mozhno "navyazat'" mnogoobraziyu takuyu prostuyu geometricheskuyu strukturu? Vo mnogih sluchayah primenima procedura, analogichnaya uzhe opisannoi nami dlya dvumernyh mnogoobrazii. Putem razrezaniya mnogoobrazie prevrashaetsya v mnogogrannik, i nado opredelit', skol'ko vershin mnogogrannika dolzhny sovmestit'sya pri obratnom abstraktnom skleivanii. Naprimer, vse 20 vershin dodekaedra, porozhdayushego prostranstvo Zeiferta-Vebera, abstraktno skleivayutsya v odnu tochku. Telesnyi ugol pri vershine evklidova dodekaedra slishkom velik dlya togo, chtoby 20 takih uglov mogli soitis' v odnoi tochke. Odnako esli etot dodekaedr pomeshen v trehmernoe giperbolicheskoe prostranstvo, to ego mozhno uvelichivat' v ob'eme do teh por, poka telesnye ugly pri vseh vershinah ne stanut dostatochno malymi, chtoby ih mozhno bylo somknut' v odnoi tochke (sm. risunok na oblozhke zhurnala). Kogda protivopolozhnye grani takogo giperbolicheskogo dodekaedra poparno abstraktno skleivayutsya (posle povorota odnoi iz nih na 3/yu polnogo oborota), to poluchennoe mnogoobrazie okazyvaetsya prostranstvom Zeiferta-Vebera s lokal'no-odnorodnoi giperbolicheskoi geometriei.

Dodekaedral'noe prostranstvo Puankare tozhe poluchaetsya skleivaniem granei dodekaedra, no pri etom 20 vershin dodekaedra razbivayutsya na pyat' grupp po chetyre vershiny v kazhdoi i zatem skleivaetsya kazhdaya chetverka. Velichina telesnogo ugla pri vershine obychnogo dodekaedra neskol'ko men'she, chem nuzhno dlya plotnogo primykaniya drug k drugu chetyreh uglov gruppy. No dostatochno bol'shoi dodekaedr v prostranstve polozhitel'noi krivizny imeet ugly kak raz nuzhnogo razmera. Takoi "uvelichennyi" dodekaedr daet vozmozhnost' vvesti v dodekaedral'nom prostranstve Puankare lokal'no-odnorodnuyu ellipticheskuyu geometriyu (sm. Ris. 13). V etoi svyazi stoit napomnit', kak zadaetsya lokal'no-odnorodnaya geometriya na trehmernom tore. Pri postroenii etogo mnogoobraziya vosem' vershin kuba abstraktno skleivayutsya. Tak kak vosem' telesnyh uglov kuba mozhno bez iskazhenii plotno prilozhit' drug k drugu v odnoi tochke, to lokal'no-odnorodnaya geometriya trehmernogo tora - evklidova. Chtoby ne vvodit' chitatelya v zabluzhdenie, nado otmetit', chto privedennye vyshe primery v deistvitel'nosti ne tipichny, tak kak oni slishkom simmetrichny. Kogda trehmernoe mnogoobrazie opredelyaetsya s pomosh'yu skleivaniya granei nepravil'nogo mnogogrannika, prihoditsya bol'she zabotit'sya o pridanii mnogogranniku takoi formy, kotoraya privedet k lokal'no-odnorodnoi geometrii na poluchennom trehmernom mnogoobrazii. Skleivaemye grani mnogogrannika dolzhny imet' odinakovuyu formu, a dvugrannye ugly mezhdu granyami, primykayushimi ko vsem skleivaemym vmeste rebram, v summe dolzhny sostavlyat' 360^o.

Mezhdu geometriei dvumernyh i trehmernyh mnogoobrazii imeyutsya po krainei mere dva glavnyh razlichiya. Vo-pervyh, krome upomyanutyh vyshe treh tipov geometrii na trehmfnyh mnogoobraziyah sushestvuet eshe pyat' drugih tipov lokal'no-odnorodnyh geometrii. Eti dopolnitel'nye geometrii poyavlyayutsya potomu, chto pri razmernosti mnogoobraziya, bol'shei dvuh, vnutrennyaya krivizna opredelyaetsya dlya kazhdogo dvumernogo secheniya, prohodyashego cherez dannuyu tochku. Lokal'no-odnorodnye geometrii na raznyh dvumernyh secheniyah ne obyazatel'no imeyut odinakovuyu kriviznu. Tem ne menee predstavlenie o vnutrennei krivizne dlya vseh vos'mi tipov trehmernyh geometrii mozhet byt' sostavleno na osnove geometrii dvumernyh mnogoobrazii.

Vtoroe razlichie mezhdu dvumernymi i trehmernymi mnogoobraziyami, kazalos' by, privodit k nepreodolimym oslozhneniyam. Trehmernye mnogoobraziya mozhno skombinirovat' takim obrazom, chto poluchitsya novoe trehmernoe mnogoobrazie, na kotorom nel'zya zadat' lokal'no-odnorodnuyu geometriyu. Odnako topologi znayut, kak razbit' trehmernoe mnogoobrazie na prosteishie chasti chisto topologicheskimi metodami.

Odin iz nas (Terston) vyskazal predpolozhenie, chto eto razbienie trehmernogo mnogoobraziya na prosteishie chasti mozhno vypolnit' tak, chto kazhdaya iz chastei dopuskaet lokal'no-odnorodnuyu geometriyu odnogo iz vos'mi vozmozhnyh tipov. Eto predpolozhenie bylo dokazano dlya shirokogo klassa mnogoobrazii, a takzhe empiricheski provereno na mnogih drugih primerah (libo vruchnuyu, libo s pomosh'yu EVM). Kontrprimerov k vyskazannoi gipoteze ne obnaruzheno, i poka ne pohozhe, chto oni voobshe budut naideny. Empiricheskii analiz, krome togo, navodit na mysl', chto dlya bol'shinstva trehmernyh mnogoobrazii uslozhnenie ih geometrii ne igraet roli. I deistvitel'no, bylo dokazano, chto na "bol'shinstve" (v nekotorom tochnom smysle etogo slova) trehmernyh mnogoobrazii mozhno zadat' lokal'no-giperbolicheskuyu geometriyu. Eto otkrytie obnadezhivaet, tak kak giperbolicheskie trehmernye mnogoobraziya obladayut mnogimi krasivymi svoistvami. Naprimer, G. Mostov iz 'el'skogo universiteta v 1971 g. dokazal, chto esli na trehmernom mnogoobrazii mozhet byt' zadana lokal'no-giperbolicheskaya geometriya, to eta geometriya vpolne opredelyaetsya topologiei mnogoobraziya. Iz etoi teoremy sleduet, chto vse mnogoobraziya, imeyushie lokal'no-odnorodnuyu geometriyu, v principe mozhno rasklassificirovat'. Krome togo, dlya giperbolicheskih trehmernyh mnogoobrazii teorema daet grubyi i prostoi kriterii identichnosti. Kogda takoe mnogoobrazie privedeno k forme, v kotoroi ono poddaetsya geometricheskomu analizu, mozhno naiti ego ob'em, a teorema garantiruet, chto etot ob'em zavisit tol'ko ot topologicheskogo tipa mnogoobraziya. Chasto pri zadanii mnogoobrazii v obshei topologicheskoi forme ih ochen' trudno razlichit'; ob'em sluzhit udobnym "indikatorom" dlya kazhdogo mnogoobraziya.

Uchityvaya eti rezul'taty, mozhno vernut'sya k nashim pervonachal'nym rassuzhdeniyam o topologicheskoi strukture Vselennoi. Nablyudeniya svidetel'stvuyut o tom, chto Vselennaya vsyudu odnorodna i imeet ellipticheskuyu, giperbolicheskuyu ili evklidovu geometriyu. Est' takzhe veskie osnovaniya priderzhivat'sya teorii, utverzhdayushei, chto v nastoyashee vremya Vselennaya nahoditsya na stadii rasshireniya, kotoraya prodolzhaetsya s momenta tak nazyvaemogo Bol'shogo vzryva. Interesno, chto ozhidaet Vselennuyu v otdalennom budushem? Po-vidimomu, imeyutsya lish' dve vozmozhnosti. Odna iz nih sostoit v tom, chto gravitacionnye sily vzaimnogo prityazheniya veshestva Vselennoi v konce koncov ostanovyat ee rasshirenie i privedut k novomu kollapsu Vselennoi v rezul'tate "bol'shogo szhatiya". Drugaya vozmozhnost' sostoit v tom, chto gravitacionnoe prityazhenie nedostatochno sil'no dlya togo, chtoby ostanovit' rasshirenie Vselennoi, i ona budet rasshiryat'sya vechno.

Soglasno odnomu iz sledstvii obshei teorii otnositel'nosti, budushee Vselennoi zavisit ot ee geometrii. Esli Vselennaya imeet ellipticheskuyu geometriyu, to ona v konce koncov snova budet kollapsirovat'. Esli ee geometriya giperbolicheskaya, to rasshirenie budet prodolzhat'sya vechno. Esli zhe geometriya Vselennoi evklidova, to ona tozhe budet vechno rasshiryat'sya, no skorost' rasshireniya budet stremit'sya k nulyu. V principe mozhno bylo by uznat', kakova geometriya Vselennoi, nametiv gigantskii treugol'nik i tochno izmeriv summu ego vnutrennih uglov. Esli by summa uglov okazalas' bol'she 180^o, to geometriya prostranstva byla by ellipticheskoi; esli by summa uglov byla ravna 180^o, to geometriya byla by evklidovoi; esli zhe summa okazalas' by men'she 180^o, to geometriya byla by giperbolicheskoi. Na samom dele kosmologi pytayutsya ocenit' srednyuyu plotnost' veshestva vo Vselennoi i skorost' ee rasshireniya, poskol'ku geometriyu Vselennoi mozhno svyazat' s etimi dvumya harakteristikami. Esli pri dannoi skorosti rasshireniya plotnost' veshestva dostatochno velika, to Vselennaya snova budet kollapsirovat'.

Mezhdu tem shiroko rasprostraneno oshibochnoe mnenie, chto krivizna Vselennoi opredelyaet, konechna ili beskonechna ee protyazhennost'. Chasto schitayut, chto esli Vselennaya konechna, to ee geometriya dolzhna byt' ellipticheskoi, i naoborot, esli geometriya Vselennoi giperbolicheskaya, to Vselennaya dolzhna byt' beskonechnoi. Primer prostranstva Zeiferta-Vebera, yavlyayushegosya trehmernym mnogoobraziem s lokal'no-giperbolicheskoi geometriei, pokazyvaet, chto ni odno iz etih ubezhdenii ng sootvetstvuet deistvitel'nosti. Na samom dele bol'shinstvo konechnyh topologicheskih modelei Vselennoi - eto trehmernye mnogoobraziya, podobnye mnogoobraziyu Zeiferta-Vebera s lokal'no-giperbolicheskoi geometriei. Takie mnogoobraziya dayut modeli konechnoi postoyanno rasshiryayusheisya Vselennoi.

Publikacii s klyuchevymi slovami: matematika - Kosmologiya - topologiya - topologiya Vselennoi Publikacii so slovami: matematika - Kosmologiya - topologiya - topologiya Vselennoi
Sm. takzhe: Razlozhenie dalekogo sveta Formirovanie galaktik v magnitnoi Vselennoi "Effekty" Zel'dovicha, zapechatlennye na nashem nebe Sverhnovaya 1994D i neozhidannaya Vselennaya Kuda smeshaetsya krasnoe smeshenie? Samaya dalekaya sverhnovaya tipa Ia Rashid Alievich Syunyaev (k semidesyatiletiyu so dnya rozhdeniya) Vse publikacii na tu zhe temu >>