1.

Okazhis' na meste kotenka Sabriny populyarnaya pevica Sabrina, ili kto drugoi iz lyudei, ne snosit' by bednyazhke golovy. Chem ne istina.

Delo v tom, chto lyudi i koshki padayut po-raznomu, kak pokazano na risunke:

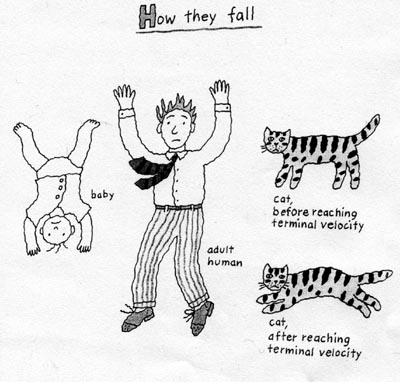
U koshki isklyuchitel'no effektivnyi vestibulyarnyi apparat, chto pozvolyaet ei bystro orientirovat'sya v prostranstve pri padenii. Koshka, izognuvshis', ochen' bystro okazyvaetsya lapami vniz v samom nachale padeniya. V rezul'tate udar raspredelyaetsya na vse chetyre lapy. Vzroslye lyudi, esli oni ne akrobaty, pri padenii kuvyrkayutsya besporyadochno i chashe vsego prizemlyayutsya na nogi i menee chasto - na golovu. Deti padayut golovoi vniz, tak kak u nih golova otnositel'no bol'shaya, chto smeshaet centr tyazhesti tela. Pri etom oni instinktivno vytyagivayut ruki. Poetomu harakternye travmy u upavshih s vysoty lyudei i koshek raznye. Lyudi chashe lomayut nogi (vzroslye) ili ruki (deti), a takzhe razbivayut cherepa. Togda kak koshki s ravnoi veroyatnost'yu lomayut vse svoi chetyre lapy [2], [3].

2.

Esli chelovek padaet s 9-go etazha, u nego men'she shansov vyzhit', chem esli by on upal s 4-go.

Kak ni stranno, u koshek vse naoborot. Statisticheskii material, sobrannyi N'yu-'orkskimi veterinarami pokazyvaet, chto pogibli tol'ko 5 procentov koshek, upavshih s vysoty 7-32-go etazha, v to vremya kak 10 procentov - pri padenii s vysoty 2-6-go etazha. Vot istina dostoinaya udivleniya. Graficheski ona pokazana nizhe (smertnost' lyudei i koshek pri padenii s raznyh vysot):

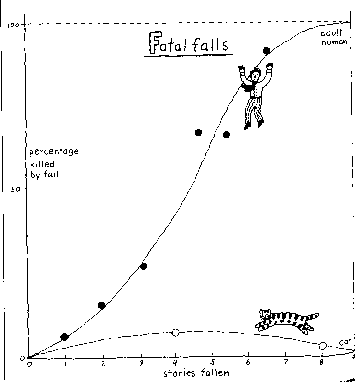
Sushestvovanie predel'noi skorosti padeniya ob'yasnyaet etot udivitel'nyi fenomen [2], [3].

3.

Pri padenii skorost' tela ne rastet vse vremya, a stremitsya k nekotoromu predel'nomu znacheniyu.

Eto legko ponyat': soprotivlenie vozduha uvelichivaetsya so skorost'yu, i v konce koncov uravnoveshivaet silu tyazhesti. S etogo momenta skorost' tela perestaet rasti, esli forma tela ne menyaetsya.

Soprotivlenie vozduha tem bol'she, chem bol'she poperechnoe sechenie tela. A sila tyazhesti opredelyaetsya massoi tela. Otnoshenie poperechnogo secheniya k masse u koshek bol'she, chem u lyudei. Poetomu predel'naya skorost' padeniya u koshki (okolo 100 km/ch) primerno dva raza men'she, chem u lyudei, i, sootvetstvenno, u nee bol'she shansov vyzhit'. No eto eshe ne vse.

4.

Vpolne veroyatno, chto forma koshki do dostizheniya predel'noi skorosti i posle ee dostizheniya raznye.

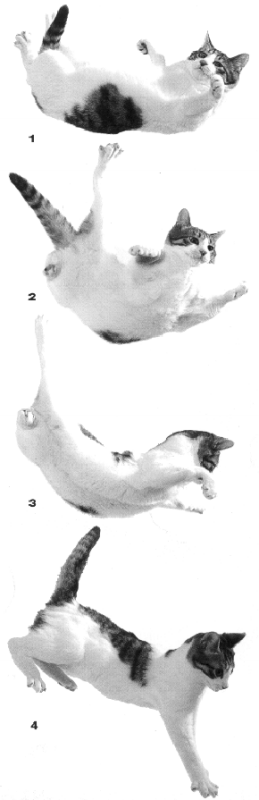
Poka koshka chuvstvuet uskorenie padeniya, ona instinktivno napryagaetsya, vygibaet spinu i vytyagivaet lapy vniz. Upav v etoi poze, koshka mozhet slomat' lapy. Hotya opyat'-taki u nee men'she shansov eto sdelat', chem u netrenirovannyh lyudei posle parashyutnogo pryzhka. Delo v tom, chto koshka padaet na sognutye lapy, smyagchaya udar pri padenii. U cheloveka takogo instinkta net. Tol'ko dlitel'nye trenirovki, takie kak u parashyutistov ili u gimnastov, mogut ego nauchit' prizemlyatsya na sognutye nogi, podobno koshke. Posle dostizheniya predel'noi skorosti uskorenie propadaet, koshka instinktivno rasslablyaetsya i prinimaet formu belki-letyagi, raskinuv lapy gorizontal'no. Eto uvelichivaet poperechnoe sechenie i umen'shaet predel'nuyu skorost' padeniya. Krome togo v takoi poze u koshki men'she shansov slomat' lapy pri udare o zemlyu, tak kak sila udara raspredelyaetsya na vsyu ploshad' i dissipiruetsya cherez myagkie tkani. Interesno, chto lapy byli slomany u bol'shinstva koshek, svalivshihsya s 7-8-go etazha, i lish' u kazhdoi trinadcatoi iz upavshih s devyatogo etazha i vyshe [2].

Teper' vernemsya k udivitel'noi sposobnosti koshek menyat' orientaciyu svoego tela vo vremya padeniya. Eto rodnit ih s baronom Myunhauzenom, kotoryi sam vytashil sebya iz bolota, shvativshis' za svoi volosy.

5.

No, v otlichie ot barona Myunhauzena, koshki pri etom ne narushayut zakonov fiziki. Naoborot, oni umelo etimi zakonami pol'zuyutsya.

Chtoby ponyat' eto, prismotrimsya pristal'nee k padayushim koshkam na risunkah vnizu:

6.

Koshka v pervuyu ochered' brosaet zlobnyi vzglyad na eksperimentatora, kotoryi v dosku ee zamuchil.

Potom rezko povorachivaet perednyuyu chast' tela vniz. Soglasno zakonu sohraneniya momenta impul'sa, zadnyaya chast' tela pri etom povorachivaetsya v protivopolozhnuyu storonu. No koshka prizhimaet perednie lapy i vytyagivaet zadnie, a takzhe operiruet hvostom, esli on u nee est' (nekotorye eksperimenty s kotom bez hvosta pokazali, chto nalichie hvosta v etom dele ne principial'no [4]). Cel' etih manipulyacii sostoit v tom, chtoby umen'shit' moment inercii perednei chasti tela i uvelichit' moment inercii zadnei chasti. Moment impul'sa raven proizvedeniyu momenta inercii na uglovuyu skorost', poetomu nesmotrya na to, chto moment impul'sa perednei chasti tela v tochnosti raven momentu impul'sa zadnei chasti, u perednei chasti uglovaya skorost' budet bol'she i, sledovatel'no, v rezul'tate ona povernetsya bol'she, chem povernetsya zadnyaya chast' tela v obratnuyu storonu. Posle etogo koshka povtoryaet tryuk v obratnom napravlenii. Tol'ko na sei raz prizhimaet zadnie lapy i vytyagivaet perednie. Vsledstvie chego ugol povorota zadnei chasti tela na etot raz budet bol'she, chem perednei chasti. V itoge, kogda oba etapa zaversheny, koshka vosstanavlivaet svoyu formu i okazyvaetsya povernutoi na nuzhnyi ugol [5],[6].

7.

Eta nehitraya nauka izmeneniya orientacii tela v prostranstve s pomosh'yu izmeneniya formy byla ponyatna lyudyam uzhe let sto nazad [7].

A koshkam, nado polagat', eto bylo izvestno s nezapamyatnyh vremen. No, okazyvaetsya, nesravnenno glubokie istiny zhdali svoego chasa i vdumchivogo nablyudatelya za poletom padayushei koshki, kotoryi zadalsya by voprosom: kakim obrazom koshka dolzhna menyat' svoyu formu, chtoby prodelat' svoi povorot naibolee ekonomnym obrazom (a vy mozhete ne somnevat'sya, chto ona delaet eto imenno tak)?

8.

Okazyvaetsya, dlya etogo koshka dolzhna reshit' pochti takoe zhe uravnenie, kotoroe opisyvaet dvizhenie kvarkov v cvetovom pole! [8],[9].

Kazhdaya raznovidnost', ili aromat kvarkov (a ih vsego shest', po krainee mere izvestnyh na segodnyashnii den') mozhet nahodit'sya v treh raznyh sostoyaniyah. Fiziki eti sostoyaniya uslovno nazyvayut cvetom. Skazhem, kvark mozhet byt' krasnym, zelenym ili sinim. Prichem vse eti cveta sovershenno ravnopravny. I to, chto opredelennye sostoyaniya kvarka my nazvali krasnym, zelenym i sinim,- eto vsego lish' uslovnoe soglashenie. Lyubye drugie tri lineino nezavisimye kombinacii iz etih sostoyanii my s takim zhe uspehom mogli by nazvat' krasnym, zelenym i sinim. Prichem nashe soglashenie o tom, chto my nazyvaem krasnym, zelenym i sinim, mozhet menyat'sya ot tochki k tochke v prostranstve-vremeni. Fizika ot etogo soglasheniya ne dolzhna zaviset', tak kak eto vsego lish' uslovnost'. Matematicheski perehod ot odnogo soglasheniya (bazisa) k drugomu zadaetsya kompleksnoi unitarnoi matricei tri na tri. Mnozhestvo takih matric sostavlyaet tak nazyvaemuyu SU(3) neabelevu gruppu (esli vam eti slova ne ponyatny, a vy tem ne menee hotite znat', kak ustroena priroda, net drugogo puti, krome izucheniya matematiki, prislushivayas' k Diraku: "Prirode prisusha ta fundamental'naya osobennost', chto samye osnovnye fizicheskie zakony opisyvayutsya matematicheskoi teoriei, apparat kotoroi obladaet neobyknovennoi siloi i krasotoi... Pochemu priroda ustroena imenno tak? Na eto mozhno otvetit' tol'ko odno: soglasno nashim sovremennym znaniyam, priroda ustroena imenno tak, a ne inache. My dolzhny prosto prinyat' eto kak dannoe. Situaciyu, veroyatno, mozhno bylo by opisat', skazav, chto Bog yavlyaetsya matematikom ochen' vysokogo ranga, i chto on pri postroenii Vselennoi ispol'zoval matematiku vysshego urovnya" [10]). No "kineticheskaya" energiya kvarkov soderzhit proizvodnye po prostranstvenno-vremennym koordinatam, i, esli matricy perehoda ot odnogo bazisa k drugomu zavisyat ot etih koordinat, pri izmenenii nashih soglashenii vozniknut dopolnitel'nye chleny, soderzhashie proizvodnye etih matric. Chtoby eti chleny ischezli (ved' real'nost' ne mozhet zaviset' ot nashih soglashenii) nado obychnye proizvodnye zamenit' na kovariantnye proizvodnye, kotorye soderzhat kompensiruyushie kalibrovochnye polya (glyuony v sluchae kvarkov). Vse eto yavlyaetsya obobsheniem principa minimal'nogo vzaimodeistviya klassicheskoi elektrodinamiki i, vkupe s kvantovymi predstavleniyami, privodit k kvantovoi hromodinamike - sovremennoi teorii sil'nyh vzaimodeistvii.

V sluchae padayushei koshki, rol' prostranstva-vremeni v vysheopisannoi konstrukcii igraet mnogoobrazie vsevozmozhnyh form koshki v ee sisteme centra mass. Chtoby sravnit' orientaciyu raznyh form koshki, nado s kazhdoi formoi zhestko svyazat' osi koordinat. No eto mozhno sdelat' beskonechno mnogimi sposobami, tak kak lyuboi povorot sistemy osei tozhe daet dopustimuyu repernuyu konfiguraciyu. Fizika (ugol povorota koshki pri posledovatel'nom izmenenii ee formy) ne dolzhna zaviset' ot proizvol'nyh soglashenii o tom, kak prikrepit' repernye osi k kazhdoi forme. Poetomu opyat' poyavlyayutsya kalibrovochnye polya, i voznikaet zadacha, matematicheski podobnaya hromodinamicheskoi probleme opisaniya dvizheniya kvarkov vo vneshnem cvetovom pole. Tol'ko na etot raz kalibrovochnoi gruppoi yavlyaetsya ne SU(3), a SO(3) - gruppa trehmernyh povorotov. Eta poslednyaya, kstati, tozhe neabeleva gruppa, i chudesnym obrazom padayushaya koshka okazyvaetsya svyazannoi s teoriei polei Yanga-Millsa - odnoi iz osnovnyh nesushih konstrukcii Standartnoi Modeli elementarnyh chastic.

9.

Koshki ne edinstvennye sushestva, "znayushie" teoriyu kalibrovochnyh polei. Kak ni stranno, eta nauka ochen' vazhna dlya mikroorganizmov.

Naprimer, dvizhenie spermatozoidov tozhe mozhno opisat' s pomosh'yu kalibrovochnyh potencialov, i, sledovatel'no, bez etoi, kazalos' by, ves'ma abstraktnoi matematicheskoi teorii nam s vami ne poyavit'sya na belom svete.

Delo v tom, chto dvizhenie mikroorganizmov proishodit pri ochen' malen'kih chislah Reinol'dsa. Chislo Reinol'dsa pokazyvaet otnositel'nuyu vazhnost' sil inercii i sil vyazkosti pri dvizhenii v gaze ili v zhidkosti. Kogda chelovek dvizhetsya cherez vozduh, chislo Reinol'dsa bol'she milliona. Pri plavanii v vode ono umen'shaetsya do desyati tysyach. Vse ravno eto ochen' mnogo, chtoby sostavit' intuitivnoe ponimanie togo, chto proishodit v mire mikroorganizmov, gde chislo Reinol'dsa mnogo men'she edinicy. Sleduyushii primer dast bolee obraznoe ponimanie etogo. Chtoby chelovek plaval pri teh zhe chislah Reinol'dsa, kak, skazhem, ego sobstvennyi spermatozoid, nado ego pomestit' v gustoe boloto i zapretit' dvigat' lyuboi chast'yu svoego tela so skorost'yu bol'she, chem odin santimetr v minutu [11].

Pri ochen' malyh chislah Reinol'dsa sily vyazkosti preobladayut, i inerciei mozhno prenebrech'. Togda v etom strannom mire plavayushih mikroorganizmov realizuetsya variant mehaniki Aristotelya: telo perestaet dvigat'sya, kak tol'ko perestayut tolkat' ego. S prenebrezheniem inerciei problema dvizheniya stanovitsya po sushestvu chisto geometricheskoi problemoi. Velichiny peremesheniya i povorota vsledstvie posledovatel'nosti izmenenii formy ne zavisyat ot togo, naskol'ko bystro eti izmeneniya proishodili, a zavisyat tol'ko ot ih geometrii, i opyat' podhodyashim matematicheskim yazykom dlya opisaniya takoi situacii okazyvaetsya teoriya kalibrovochnyh polei [8].

10. 

"Nepostizhimaya effektivnost' matematiki v estestvennyh naukah ... eto chudesnyi dar, kotoryi my ne ponimaem i kotorogo ne zasluzhivaem" [12].

Eti slova Vignera nevol'no vspominaesh', vidya, kak pereplelis' mezhdu soboi s pomosh'yu matematiki padayushaya koshka, kvarki i plavayushie infuzorii. Vot eshe odin primer takogo zhe roda. U pchel est' ves'ma slozhnyi simvol'nyi yazyk tanca s pomosh'yu kotorogo pchela soobshaet svoim sorodicham rasstoyanie i napravlenie do istochnika pishi [13]. Sushestvovanie takogo yazyka u pchel - fakt sam po sebe tainstvennyi i dostoinyi voshisheniya. No vot matematik Barbara Shipman (Barbara Shipman) zametila [14] v figurah etogo tanca proyavleniya shestimernogo flagovogo mnogoobraziya, ezotericheskoi matematicheskoi konstrukcii, kotoruyu ispol'zuyut fiziki pri izuchenii kvantovoi hromodinamiki. I to ne vse, a tol'ko matematicheski ochen' prodvinutye.

Chto eto, sluchainoe sovpadenie ili ocherednoe proyavlenie "nepostizhimoi effektivnosti matematiki" - poka neizvestno.

No vernemsya k padayushei koshke. Nesmotrya na sovershenstvo koshach'ei akrobatiki, razlichnye povrezhdeniya vse ravno veroyatny pri padenii s bol'shoi vysoty. Poetomu mozhno predpolozhit', chto evolyuciya vyrabotala u koshek nekii mehanizm isceleniya.

11.

Kak ni stranno, uchenye podozrevayut, chto murlykan'e koshki i est' etot samyi mehanizm [15],[16]!

Vozmozhno, nizkochastotnye vibracii toi chastoty i toi intensivnosti, kotoruyu sozdayut koshki pri murlykanii, obladayut terapevticheskim effektom [16].

No eto uzhe odinnadcataya istina, togda kak dlya spokoinogo sna trebovalos' vsego lish' desyat'. No gryadut i drugie dni, i vasha dusha snova stanet iskat' istiny, naprimer kakov molekulyarnyi mehanizm evolyucii, kotoraya nadelila koshek stol' sovershennymi svoistvami [17]. Ibo "vse davno uzhe skazano, no tak kak nikto ne slushaet, prihoditsya postoyanno vozvrashat'sya nazad i povtoryat' vse snachala" [18].