 K voprosu o matematicheskoi datirovke pravoslavnoi pashalii
K voprosu o matematicheskoi datirovke pravoslavnoi pashalii28.09.2004 2:45 | V. A. Uvarov
V poslednee vremya v literature obsuzhdaetsya vozmozhnost' datirovki pravoslavnoi pashalii po sovpadeniyu dat pashal'nyh i astronomicheskih polnolunii (sm., naprimer, [1, 2]). Metod bezuslovno interesnyi, no v rassmatrivaemom vide on imeet opredelennyi nedostatok. Delo v tom, chto pravoslavnye pashal'nye polnoluniya yavlyayutsya kalendarnymi datami Vechnogo lunno-solnechnogo cerkovnogo kalendarya (podrobnosti sm. v [3], a takzhe v citiruemoi tam literature). Poetomu logichnee sravnivat' s astronomicheskimi fazami Luny ne tol'ko pashal'nye polnoluniya, no ves' Vechnyi kalendar' v celom. Poterya informacii pri ispol'zovanii tol'ko pashal'nyh polnolunii mozhet privesti k uvelicheniyu pogreshnosti poluchennogo rezul'tata.
Vechnyi kalendar' predpolagaet 19-letnii cikl Metona v yulianskom kalendare absolyutno tochnym, t.e. kalendar' sostavlen na 19 let, imeyushih rovno 235 lunnyh mesyacev, a zatem ciklicheski povtoryaetsya. Poryadkovyi nomer goda v 19-letnem cikle opredelyaetsya "zolotym chislom", kotoroe ravno uvelichennomu na edinicu ostatku ot deleniya nomera goda po nashemu letoschisleniyu na 19. Gody, u kotoryh "zolotye chisla" ravny 3, 6, 8, 11, 14, 17 i 19, imeyut po 13 mesyacev, ostal'nye - po 12. Mesyacy s nechetnymi poryadkovymi nomerami v godu imeyut po 30 dnei, s chetnymi - po 29, prichem 29 fevralya ne uchityvaetsya pri opredelenii dliny mesyaca, a poslednii 235-yi mesyac cikla imeet 29 dnei. Pervyi den' kazhdogo mesyaca yavlyaetsya kalendarnym novoluniem, chetyrnadcatyi - kalendarnym polnoluniem. Pervoe kalendarnoe novolunie v 19-letnem cikle prihoditsya na 23 yanvarya po st. st.
V real'nosti 19-letnii cikl Metona ne yavlyaetsya tochnym. Poetomu Vechnyi kalendar', horosho soglasuyushiisya s fazami Luny v odnom iz 19-letii, budet zapazdyvat' otnositel'no faz Luny primerno na odni sutki cherez kazhdye 307 let. Etoi osobennost'yu mozhno vospol'zovat'sya dlya datirovki Vechnogo kalendarya, a znachit i pravoslavnoi pashalii.
V kachestve kriteriya sovpadeniya Vechnogo kalendarya s fazami Luny v vybrannom 19-letii rassmotrim usrednennyi interval vremeni Tsr mezhdu nachalom sutok kalendarnogo novoluniya i momentom sootvetstvuyushego astronomicheskogo novoluniya. Usrednenie provedem po vsem 235 novoluniyam v vybrannom 19-letii, nachinayushimsya s goda s "zolotym chislom" ravnym edinice. Vse momenty vremeni opredelim po aleksandriiskomu vremeni (vremya po Grinvichu plyus dva chasa), nachalom sutok kalendarnogo novoluniya budem schitat' polnoch', daty i vremya astronomicheskih novolunii voz'mem iz tablic [4].
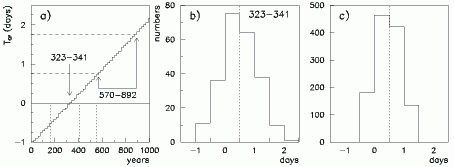
Ris.1. Usrednennyi interval vremeni Tsr (v sutkah) mezhdu nachalom sutok kalendarnogo novoluniya i momentom astronomicheskogo novoluniya v 0-1000 gg. n.e. (a). Raspredelenie momentov astronomicheskih novolunii po dnyam kalendarnyh lunnyh mesyacev v 323-341 gg. (b) i po dnyam "nesmeshennogo mesyaca nisana" (s). Ispol'zuetsya aleksandriiskoe vremya. |
Velichina usrednennogo intervala vremeni Tsr byla vychislena dlya kazhdogo 19-letiya pervyh desyati vekov n.e. Zavisimost' Tsr ot nomera goda po nashemu letoschisleniyu pokazana na Ris.1a (gistogramma). Naimen'shee po absolyutnoi velichine znachenie Tsr = 5 min prihoditsya na 19-letie s 323 po 341 gg. Dlya etogo 19-letiya na Ris.1b pokazano raspredelenie momentov astronomicheskih novolunii po dnyam sootvetstvuyushih lunnyh mesyacev Vechnogo kalendarya (na gorizontal'noi osi risunka cifroi 1 oboznachen pervyi den' sootvetstvuyushego mesyaca, cifroi 0 - poslednii den' predydushego mesyaca, i t.d.). Takim obrazom, esli nachalom kazhdogo mesyaca v Vechnom kalendare po opredeleniyu yavlyaetsya srednee novolunie, to mozhno sdelat' vyvod, chto Vechnyi kalendar' sozdan na osnove astronomicheskih dannyh o fazah Luny v tom zhe 19-letii, v kotorom prohodil Pervyi Nikeiskii sobor (325 g.).
Izvestno, chto v drevnem iudeiskom kalendare, ustanavlivaemom "po pokazaniyam svidetelei", nachalom mesyaca schitalas' neomeniya - pervoe poyavlenie lunnogo serpa na vechernem nebe. A kak obstoit delo v deistvuyushem "vychislyaemom" iudeiskom kalendare? Chtoby otvetit' na etot vopros, vospol'zuemsya temi zhe astronomicheskimi tablicami [4] i formuloi Gaussa dlya opredeleniya daty iudeiskoi Pashi (sm., naprimer, [2]), kotoraya perevodit datu 15-go nisana iudeiskogo kalendarya (a znachit i datu 1-go nisana - nachala mesyaca) v datu yulianskogo kalendarya. Pri etom uchtem, chto v iudeiskom kalendare iz-za mnogochislennyh religioznyh predpisanii, otnosyashihsya k kalendarnym prazdnikam, a takzhe dlya podderzhaniya srednei prodolzhitel'nosti goda nachalo mesyaca, opredelennoe po otnosheniyu k moledu - srednemu novoluniyu, chasto sdvigaetsya vpered na odin ili dazhe na dva dnya. Itak, opredelim v yulianskom kalendare pervyi den' "nesmeshennogo mesyaca nisana" po formule Gaussa, no bez predpisannyh sdvizhek.
Na Ris.1c dlya pervyh dvenadcati vekov n.e. pokazano raspredelenie po dnyam "nesmeshennogo mesyaca nisana" momentov sootvetstvuyushih astronomicheskih novolunii, opredelennyh po aleksandriiskomu vremeni. Nachalo "nesmeshennogo mesyaca nisana" (polnoch' v nachale pervyh sutok - vertikal'naya shtrihovaya liniya na Ris.1c) nastupaet primerno cherez 55 minut posle srednego novoluniya. Takim obrazom, v period s 323 po 341 gg. nachalo lunnyh mesyacev v Vechnom kalendare opredelyaetsya tak zhe, kak i nachalo "nesmeshennogo mesyaca nisana" v deistvuyushem iudeiskom kalendare. Vysheperechislennye harakteristiki privodyat k naibolee veroyatnomu resheniyu zadachi o datirovke Vechnogo kalendarya po fazam Luny - Vechnyi kalendar' byl sozdan na Pervom Nikeiskom sobore v 325 g.
Odnako, eto ne edinstvennoe reshenie. Drugoe reshenie zadachi mozhet byt' polucheno iz predpolozheniya, chto Vechnyi kalendar' sostavlen takim obrazom, chtoby srednee polnolunie prihodilos' na chetyrnadcatye sutki lunnogo mesyaca, t.e. na kalendarnoe polnolunie. V etom sluchae upomyanutyi vyshe usrednennyi interval vremeni Tsr dolzhen nahodit'sya v diapazone ot (1/2)L-14 = 0,765 sutok do (1/2)L-13 = 1,765 sutok, gde L - prodolzhitel'nost' lunnogo sinodicheskogo mesyaca. Ispol'zuya dannye, pokazannye na Ris.1a, nahodim, chto etomu diapazonu sootvetstvuet period vremeni s 570 po 892 gg. Takim obrazom, eto vtoroe reshenie zadachi o datirovke Vechnogo kalendarya po fazam Luny.
Chtoby razreshit' poluchennuyu neodnoznachnost' v datirovke po fazam Luny, vospol'zuemsya datirovkoi po vesennemu ravnodenstviyu. Vspomnim, chto soglasno sed'momu apostol'skomu pravilu zapreshaetsya sovershat' Pashu "prezhde vesennego ravnodenstviya s iudeyami", i chto odnim iz osnovnyh otlichii Vechnogo kalendarya ot deistvuyushego iudeiskogo yavlyaetsya zapazdyvanie kalendarnyh pashal'nyh polnolunii primerno na odin lunnyi mesyac po otnosheniyu k iudeiskim dva raza za 19-letnii cikl (v gody s "zolotymi chislami" ravnymi 8 i 19). Sed'moe apostol'skoe pravilo bylo, bezuslovno, aktual'nym kak v gody vvedeniya etogo pravila (inache zachem bylo by ego vvodit'!), tak i v gody sostavleniya Vechnogo kalendarya - imenno etim pravilom obuslovleno upomyanutoe zapazdyvanie. Opredelim, kogda po nashemu letoschisleniyu rovno dva kalendarnyh polnoluniya v 19-letnem cikle, sootvetstvuyushie iudeiskim pashal'nym, byli do vesennego ravnodenstviya, i ubedimsya, chto eti polnoluniya prihodilis' na gody s "zolotymi chislami" ravnymi 8 i 19.
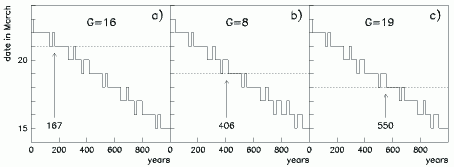
Ris.2. Daty vesennego ravnodenstviya v yulianskom kalendare po aleksandriiskomu vremeni v 0-1000 gg. n.e. dlya godov s "zolotymi chislami" G=16, G=8 i G=19. |
V Vechnom kalendare v gody s "zolotymi chislami" ravnymi 8 i 19 predpashal'nye (t.e. nastupayushie za mesyac do pashal'nyh, no sootvetstvuyushie iudeiskim pashal'nym) polnoluniya popadayut sootvetstvenno na 19 i 18 marta po st. st., a samoe rannee pashal'noe polnolunie popadaet na 21 marta po st. st. v god s "zolotym chislom" ravnym 16. Na Ris.2a,b,c pokazano, kak v yulianskom kalendare po aleksandriiskomu vremeni v raznye gody nashego letoschisleniya, no s rassmatrivaemymi "zolotymi chislami" G=16, 8 i 19, eti daty (gorizontal'nye linii) sootnosyatsya s datami vesennego ravnodenstviya (gistogrammy), vychislennymi po privedennym v [5] formulam. Pashal'noe polnolunie v god s G=16 bylo do vesennego ravnodenstviya poslednii raz v 167 g., a predpashal'nye polnoluniya v gody s G=8 i 19 - sootvetstvenno v 406 i 550 gg.
Takim obrazom, do 167 g. kalendarnye polnoluniya, sootvetstvuyushie iudeiskim pashal'nym, byli do vesennego ravnodenstviya tri (G=16, 8 i 19) i bolee raz za kazhdye devyatnadcat' let, s 167 po 406 gg. - dva raza (G=8 i 19), s 406 po 550 gg. - odin raz (G=19), a posle 550 g. takie polnoluniya nikogda ne byli do vesennego ravnodenstviya. Poetomu resheniem zadachi o datirovke po vesennemu ravnodenstviyu yavlyaetsya utverzhdenie, chto Vechnyi kalendar' byl sozdan v period s 167 po 406 gg., chto isklyuchaet vtoroe reshenie zadachi o datirovke po fazam Luny, dazhe s uchetom vozmozhnoi pogreshnosti v odni sutki, s kotoroi v IV-VI vekah n.e. mogli opredelyat'sya daty vesennego ravnodenstviya.
Podoidem k zadache o datirovke po vesennemu ravnodenstviyu neskol'ko po-inomu. Pri sozdanii Vechnogo kalendarya vesennee ravnodenstvie ne moglo byt' pozzhe 21 marta po st. st. (inache v god s "zolotym chislom" ravnym 16 Pasha prazdnovalas' by ne v marte, a v aprele) i ran'she 20 marta po st. st. (inache v god s "zolotym chislom" ravnym 8 Pasha prazdnovalas' by ne v aprele, a v marte). Ishodya iz etogo, poluchaem neskol'ko bolee zhestkoe ogranichenie, chto Vechnyi kalendar' byl sozdan v 192-359 gg., t.e. togda, kogda vesennee ravnodenstvie bez isklyuchenii prihodilos' na 20 ili na 21 marta po st. st.
Reshenie matematicheskoi zadachi o datirovke Vechnogo kalendarya odnovremenno po fazam Luny i po vesennemu ravnodenstviyu privodit k okonchatel'nomu utverzhdeniyu, chto Vechnyi kalendar' - pravoslavnaya pashaliya byl sozdan na Pervom Nikeiskom sobore v 325 g. (vozmozhno, posle podgotovitel'nogo perioda, nachavshegosya v konce II veka n.e.), a takzhe k sleduyushim vyvodam.
Vo-pervyh, pravoslavnaya Pasha prazdnuetsya v pervoe voskresen'e posle chetyrnadcatogo dnya pashal'nogo lunnogo mesyaca - 14-oi Luny. Pri etom, srednee astronomicheskoe polnolunie v 325 g., kogda byl sozdan Vechnyi kalendar', prihodilos' na den' 15-oi Luny, i tol'ko v period s 570 po 892 gg. - na den' 14-oi Luny. Eto oznachaet, chto otnosyasheesya k Vechnomu kalendaryu slovosochetanie "14-aya Luna ili pashal'noe polnolunie" stalo sootvetstvovat' svoemu smyslu (ili dazhe vozniklo) lish' v konce VI veka. Do etogo vremeni kalendarnoe pashal'noe polnolunie nosilo mnogo razlichnyh nazvanii: pashal'naya granica, faska, zakonnaya Pasha i t.p.
Vo-vtoryh, esli 14-aya Luna prihoditsya na subbotu, to pravoslavnaya Pasha prazdnuetsya v den' 15-oi Luny v voskresen'e. Poskol'ku v 325 g. nachalo pashal'nogo lunnogo mesyaca v Vechnom kalendare i nachalo "nesmeshennogo mesyaca nisana" v deistvuyushem iudeiskom byli opredeleny v srednem odinakovo (krome godov s "zolotymi chislami" ravnymi 8 i 19), to v IV-VIII vekah den' 15-oi Luny vremya ot vremeni sovpadal s dnem 15-go nisana, a esli eto bylo voskresen'e, to pravoslavnaya Pasha sovpadala s iudeiskoi. Takoe sovpadenie ne protivorechit sed'momu apostol'skomu pravilu. Inogda eto pravilo formuliruetsya v vide dvuh nezavisimyh punktov: "a) ne sovershat' Pashu prezhde vesennego ravnodenstviya i b) ne sovershat' ee s iudeyami", chto ne ekvivalentno pervonachal'noi formulirovke: v pravile nichego ne govoritsya, kak prazdnovat' Pashu (vmeste ili ne vmeste s iudeyami) posle vesennego ravnodenstviya.
V-tret'ih, tot fakt, chto v 323-341 gg. lunnye mesyacy v Vechnom kalendare i "nesmeshennyi mesyac nisan" v deistvuyushem iudeiskom nachinalis' v odnu i tu zhe fazu Luny - v srednee novolunie, daet vse osnovaniya predpolagat', chto otcy Nikeiskogo sobora schitali kalendarnyi den' 14-oi Luny kak istinnoe 14-oe nisana, kogda dolzhna sovershat'sya vethozavetnaya (zakonnaya, t.e. po zakonu Moiseya) Pasha. Poetomu pervoe pravilo Antiohiiskogo sobora, kotoroe zapreshaet "osobitisya i so iudeyami sovershati Pashu", sleduet ponimat', kak otnosyasheesya imenno k opredelyaemoi Vechnym kalendarem zakonnoi Pashe, a ne k fakticheskoi praktike iudeev. Togda, deistvitel'no, zakonnaya Pasha vsegda predshestvuet Pashe pravoslavnoi, nastupayushei v istinnoe 15-oe nisana ili pozzhe.
Posle 783 g., kogda pravoslavnaya Pasha navsegda razoshlas' s iudeiskoi, raznochteniya upomyanutyh vyshe kanonicheskih pravil opredeleniya daty Pashi uzhe ne yavlyayutsya aktual'nymi.
V 1582 g. papa Grigorii XIII reformiroval yulianskii kalendar' i pashaliyu: Solnce i Luna byli "postavleny na mesto", a takzhe prinyaty mery, chtoby vpred' oni "so svoih mest nikogda ne sdvigalis'". Odnako, esli ekstrapolirovat' grigorianskuyu pashaliyu nazad, to vidno, chto Solnce (den' vesennego ravnodenstviya) bylo postavleno tuda, gde ono bylo v III veke, a Luna (den' polnoluniya) - tuda, gde ona byla v VII veke. V rezul'tate takoi neposledovatel'nosti srednee astronomicheskoe polnolunie, kotoroe v god sozdaniya Vechnogo kalendarya prihodilos' na den' 15-oi Luny, v grigorianskoi pashalii vsegda prihoditsya na den' 14-oi Luny. Eto znachit, chto reformatory vveli dopolnitel'nuyu "ne svyazannuyu s astronomiei" popravku, i tem samym narushili pervonachal'nyi zamysel sozdatelei Vechnogo kalendarya.
Kak zhe eto ob'yasnit'? Izvestno, chto rimskaya cerkov' eshe dolgo posle Pervogo Nikeiskogo sobora pol'zovalas' svoei sobstvennoi pashaliei, odnim iz otlichii kotoroi bylo to, chto rimlyane ne prazdnovali Pashu na sleduyushii den', a perenosili ee na nedelyu pozzhe, esli kalendarnyi den' 14-oi Luny prihodilsya na subbotu [2]. Eto znachit, chto uzhe v IV veke rimlyane v kachestve pashal'noi granicy ispol'zovali ne 14-yi den' Luny, a den' srednego astronomicheskogo polnoluniya, kotoryi v to vremya prihodilsya na 15-yi den' Luny. I tol'ko v VI veke, kogda srednee polnolunie peremestilos' na den' 14-oi Luny, rimskaya cerkov' pereshla na Vechnyi kalendar'. Takim obrazom, Grigorii XIII postavil Lunu ne tuda, gde ona byla vo vremya Nikeiskogo sobora, a tuda, gde ona byla, kogda rimskaya cerkov' prinyala Vechnyi kalendar'.
Spisok literatury
1.
Nosovskii G.V., Fomenko A.T. Matematicheskaya hronologiya bibleiskih
sobytii. M., Nauka, 1997.
2.
Krasil'nikov Yu.D. "Solnce, Luna, drevnie prazdniki i novomodnye teorii".
Astronomiya protiv "novoi hronologii", M., Russkaya panorama, 2001.
3.
Efrosman A.M. "K voprosu o proishozhdenii nashego letoschisleniya".
Istoriko-astronomicheskie issledovaniya, vyp. XVII, M., Nauka, 1984.
4.
Espenak F. Five Millennia Catalog of Phases of the Moon.
NASA / Goddard Space Flight Center, 2000.
5. Meeus J. Astronomical Algorithms. Willmann-Bell, Inc., Richmond,
1991.
|
Publikacii s klyuchevymi slovami:
kalendar'
Publikacii so slovami: kalendar' | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |