Astronet > Maksvella raspredelenie

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Na saite

Astrometriya

Astronomicheskie instrumenty

Astronomicheskoe obrazovanie

Astrofizika

Istoriya astronomii

Kosmonavtika, issledovanie kosmosa

Lyubitel'skaya astronomiya

Planety i Solnechnaya sistema

Solnce

Maksvella raspredelenie

- raspredelenie chastic (molekul, atomov) ideal'nogo gaza no skorostyam v usloviyah termodinamicheskogo (teplovogo) ravnovesiya. M. r. bylo vyvedeno v 1860 g. angl. fizikom Dzh.K. Maksvellom na osnove modeli, v k-roi gaz rassmatrivaetsya kak sovokupnost' ogromnogo chisla malen'kih, absolyutno uprugih sharov, nahodyashihsya v sosude s zadannoi temp-roi T stenok. Soglasno M. r., sr. chislo chastic $\Delta n$ , imeyushih abs. velichinu skorosti v intervale ot v do $v+\Delta v$ , opredelyaetsya vyrazheniem:
$\Delta n=N\cdot 4\pi\cdot \left({m\over{2\pi kT}}\right)^{3/2}\cdot e^{-mv^2/2kT}\cdot v^2\cdot \Delta v$ , (*)
gde N - polnoe chislo chastic v sisteme. M. r. poluchilo pryamoe podtverzhdenie v serii opytov s molekulyarnymi puchkami. Krome togo, zakonomernosti protekaniya celogo ryada fiz. processov v gazah ubeditel'no svidetel'stvuyut o spravedlivosti M. r. (napr., doplerovskoe ushirenie spektr. linii, osobennosti ionizacii atomov i dissociacii molekul).

M. r. sygralo chrezvychaino vazhnuyu rol' v stanovlenii i razvitii kinetich. teorii gazov i statnstich. fiziki. V 1877 g. avstr. fizik L. Bol'cman vyvel bolee obshee raspredelenie, nazvaemoe Bol'cmana raspredeleniem chastic ideal'nogo gaza no energiyam. iz k-rogo mozhno poluchit' M. r., esli prenebrech' vsemi vidami energii, krome kinetich. energii chastic $\varepsilon_k=mv^2/2$ . V sootvetstvii s (*) chislo chastic kak s malymi, tak i s ochen' bol'shimi skorostyami malo (ris.). Maksimum raspredeleniya sootvetstvuet skorosti $v_n=\sqrt{2kT/m}$ (v_n - naibolee veroyatnaya skorost'). Vazhnoe fiz. znachenie imeet sr. kvadratichnaya skorost' $\bar{v^2}=(3/2)v^2_n$ , opredelyayushaya sr. kinetich. energiyu chastic $\bar{\varepsilon_{kin}}=m\bar{v^2}/2=(3/2)kT$ , k-raya ne zavisit ot massy chastic. Poetomu v ideal'nom gaze, sostoyashem iz chastic razlichnyh sortov (elektronov, ionov), v usloviyah termodinamich. ravnovesiya vse chasticy, nezavisimo ot ih sorta, obladayut odinakovoi sr. kinetich. energiei. Otsyuda sleduet, chto naibol'shie skorosti imeyut chasticy s naimen'shei massoi. Tak, v termodinamicheski ravnovesnoi plazme sr. abs. velichina skorosti elektronov e v $\sqrt{m_p/m_e}=43$ raza bol'she skorosti protonov r, a eta poslednyaya, v svoyu ochered', v 4 raza prevyshaet skorost' atomov kisloroda. M. r. po odnomu komponentu skorosti imeet gaussovskii harakter, t.e. ego maksimum prihoditsya na nulevuyu skorost', a snizhenie krivoi raspredeleniya v e raz sootvetstvuet skorosti, ravnoi $\sqrt{2kT/m}$ .

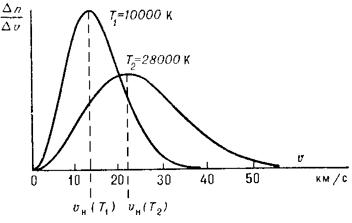
Raspredelenie atomov ionizovannogo vodoroda
(protonov) po skorostyam v pri dvuh
znacheniyah absolyutnoi temperatury T₁ i T₂
(T₁ < T₂), primerno sootvetstvuyushih
effektivnym temperaturam zvezd spektral'nyh
klassov AO i VO. Polnoe chislo chastic v oboih
sluchayah odinakovo.

Iz M. r. sleduet, chto nek-roe kolichestvo chastic mozhet dostigat' skorostei, znachitel'no prevyshayushih v_H. Takie chasticy obladayut otnositel'no bol'shimi energiyami i poetomu igrayut vazhnuyu rol' v kosmich. fizike i astrofizike, hotya ih chislo otnositel'no neveliko (dolya chastic s abs. znacheniem skorosti $v\gg v_n$ proporcional'na $e^{v^2/v_n^2}$ ). Chasticy s vysokimi skorostyami imeyut opredelyayushee znachenie, napr., v dissipacii atmosfer planet, v termoyadernyh reakciyah v nedrah zvezd. Kak sleduet iz opredeleniya, M. r. primenimo dlya ideal'nogo gaza, nahodyashegosya v termodinamicheskom ravnovesii. Blizkie k etomu trebovaniyu usloviya sozdayutsya dlya plazmy v zvezdah glavnoi posledovatel'nosti. Odnako na pozdnih stadiyah evolyucii zvezd v plotnyh yadrah krasnyh gigantov i sverhgigantov, a takzhe v sverhplotnyh ob'ektah - belyh karlikah i neitronnyh zvezdah - sv-va zvezdnogo veshestva sushestvenno izmenyayutsya. V etom sluchae chasticy s polucelym spinom (elektrony, neitrony, protony i dr.) obrazuyut vyrozhdennyi gaz, opisyvaemyi bolee obshim raspredeleniem Fermi-Diraka. S umen'sheniem plotnosti veshestva pri k.-l. fiksirovannoi temp-re, udovletvoryayushei neravenstvu $0 < kT \ll m_e c^2$ , raspredelenie Fermi-Diraka perehodit v M. r. Pri zvezdnyh vzryvah (sm. Gravitacionnyi kollaps, Sverhnovye zvezdy), a takzhe vblizi neitronnyh zvezd temp-ra veshestva mozhet byt' ochen' vysokoi ( $kT \ge m_e c^2$ ) pri sravnitel'no umerennoi plotnosti. Zdes' obychnoe M. r. (*) uzhe neprigodno dlya elektronnogo gaza. Vmesto nego inogda primenyayut relyativistskoe M. r., k-roe mozhno poluchit' iz raspredeleniya Bol'cmana, vospol'zovavshis' relyativistskoi svyaz'yu mezhdu kinetich. energiei $\varepsilon_{kin}$ i skorost'yu v: $\varepsilon_{kin}=m_e c^2 (\gamma-1)$ , gde $\gamma=1/\sqrt{1-(v/c)^2}$ . Odnako pri temp-rah $kT \ge m_e c^2$ proishodit mnozhestvennoe rozhdenie elektron-pozitronnyh par. Poetomu relyativistskoe M. r. mozhno ispol'zovat' lish' v kachestve pervogo priblizheniya. Bolee tochnoe rassmotrenie dolzhno osnovyvat'sya na raspredelenii Fermi-Diraka s uchetom relyativistskih f-l dlya impul'sa i energii chastic.

M. r. shiroko ispol'zuetsya dlya opisaniya fiz. processov v mezhzvezdnoi i mezhplanetnoi sredah. Odnako ne vsegda veshestvo mozhno schitat' v etih sredah nahodyashimsya v termodinamich. ravnovesii. Tak, vsledstvie sil'nogo razlichiya mass elektronov i ionov obmen energiei mezhdu nimi zatrudnen. Poetomu chasto sozdayutsya usloviya, kogda ne uspevaet ustanovit'sya M. r., obshee dlya elektronov i ionov. Tem ne menee mnogie astrofizich. zadachi udaetsya uspeshno reshit', rassmatrivaya elektronnyi i ionnyi gazy kak slabo svyazannye sistemy, opisyvaemye M. r. s razlichnymi temp-rami: elektronnoi i ionnoi.

(D.K. Nadezhin)

D. K. Nadezhin, "Fizika Kosmosa", 1986
Glossarii Astronet.ru

A | B | V | G | D | Z | I | K | L | M | N | O | P | R | S | T | U | F | H | C | Ch | Sh | E | Ya

Publikacii s klyuchevymi slovami: raspredelenie Maksvella Publikacii so slovami: raspredelenie Maksvella
Sm. takzhe: Maksvella raspredelenie

Obsudit' etu publikaciyu

Versiya dlya pechati