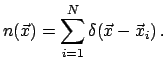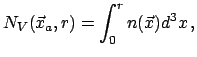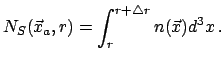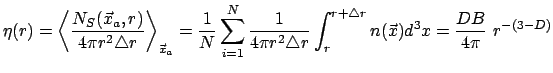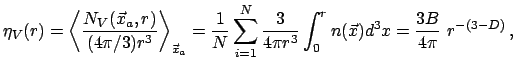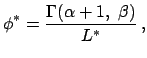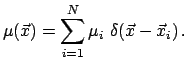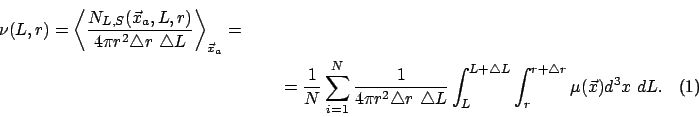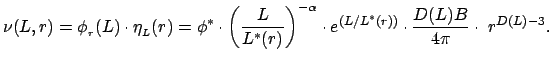<< 2. Nablyudatel'nye dannye | Oglavlenie | 4. Metody analiza struktury >>
3. Sposoby opisaniya struktury
Pri opisanii krupnomasshtabnoi struktury seichas, kak pravilo, ispol'zuetsya dva tipa modelei: odnorodnaya model' s fluktuaciyami plotnosti, a takzhe fraktal'naya model'. Obe eti modeli obladayut kak dostoinstvami, tak i nedostatkami.
Odnorodnoe raspredelenie, na kotoroe nakladyvayutsya fluktuacii plotnosti konechnoi amplitudy, udobno dlya analiticheskogo opisaniya struktury. V to zhe vremya real'no nablyudaemye osobennosti struktury - ee samopodobie v znachitel'nom intervale masshtabov, otsutstvie nadezhno vydelyaemyh centrov koncentracii i t. p. - luchshe opisyvayutsya v ramkah fraktal'noi modeli. V poslednie gody fraktal'nye modeli dostatochno shiroko ispol'zuyutsya kak v astrofizike, tak i v fizike voobshe. Dlya mnogih sistem fraktal'nye modeli yavlyayutsya prosteishimi sposobami opisaniya struktury, chem, v chastnosti, ob'yasnyaetsya ih populyarnost'. V to zhe vremya principial'naya neanalitichnost' fraktal'nyh modelei sozdaet znachitel'nye trudnosti pri opisanii processov, privodyashih k formirovaniyu struktur takogo roda. Bolee podrobno obshie svoistva fraktal'nyh modelei rassmatrivalis' v lekcii, prochitannoi na XXXII Shkole v 2003 g.
Ponyatie plotnosti zhidkosti/gaza, obychno ispol'zuemoe v gidrodinamike, soderzhit predpolozhenie o tom, chto sushestvuet znachenie plotnosti, ne zavisyashee ot velichiny elementa ob'ema. Togda mozhno opredelit' plotnost' kak funkciyu prostranstvennyh koordinat (kak pravilo, nepreryvnuyu). V zadache analiza fluktuacii funkciya plotnosti mozhet byt' realizaciei stohasticheskogo processa, dlya kotorogo opredeleny obychnye momenty - srednee, dispersiya i t. d. V chastnosti, eto mozhet byt' i diskretnyi process, soderzhashii konechnoe chislo tochek, naprimer, puassonovskii process.
V sluchae fraktal'nyh struktur ponyatiya plotnosti chisla chastic v
tochke ne sushestvuet, tak kak v kazhdom elemente ob'ema struktury
soderzhitsya ierarhiya klasterov i znachenie koncentracii sushestvenno
zavisit ot velichiny elementa ob'ema. Dlya opisaniya nepreryvnoi
ierarhii skuchivaniya, yavlyayusheisya novoi harakteristikoi processa,
neobhodimo vvesti special'nuyu nezavisimuyu peremennuyu - radius
oblasti (
), v kotoroi proizvoditsya podschet chastic. Pri etom
chislo chastic samopodobnoi struktury rastet po stepennomu zakonu
gde
- fraktal'naya razmernost';
opredelyaetsya
chislom ob'ektov 
vnutri masshtaba nulevogo urovnya 
.
Rassmotrim diskretnyi stohasticheskii process, realizacii kotorogo
predstavlyayut sovokupnosti chastic, raspolozhennyh v sluchaino
vypavshih polozheniyah
, tak chto
realizovannaya plotnost' chisla chastic
daetsya
vyrazheniem
Esli stohasticheskii process yavlyaetsya fraktal'nym, to dlya ego opisaniya neobhodimo rassmotret' dopolnitel'nuyu «fraktal'nuyu» peremennuyu
, harakterizuyushuyu stepen' singulyarnosti fraktal'noi
struktury. Pust'
oboznachaet chislo chastic v
share radiusa s centrom v tochke 
, prinadlezhashei
strukture:
i
- chislo chastic v obolochke
c centrom v tochke struktury :
Pri perehode ot realizacii k realizacii eti velichiny ispytyvayut
fluktuacii, posle osredneniya kotoryh po mnozhestvu realizacii
ostaetsya zavisimost' ot masshtaba . V sluchae ergodicheskih
processov osrednenie po realizaciyam mozhno zamenit' osredneniem po
mnozhestvu tochek odnoi realizacii. Opredelim uslovnuyu koncentraciyu
stohasticheskogo fraktal'nogo processa v vide
i ob'emnuyu uslovnuyu koncentraciyu v vide
gde
oznachaet usrednenie,
provodimoe pri uslovii, chto centry sharov nahodyatsya v tochkah,
zanyatyh chasticami realizacii (otsyuda nazvanie «uslovnaya»), a
poslednie ravenstva v (5) i (6) otnosyatsya k
ideal'nym fraktal'nym strukturam (1), dlya kotoryh
. Pokazatel' stepeni v uslovnoi
koncentracii
nazyvaetsya fraktal'noi korazmernost'yu struktury.
Principial'no vazhnym svoistvom uslovnoi koncentracii yavlyaetsya to,
chto dlya processov s konechnym masshtabom fraktal'nosti, posle
kotorogo raspredelenie chastic stanovitsya odnorodnym, statistiki
(5) i (6) vyhodyat na postoyannoe znachenie,
chto sootvetstvuet ravenstvu 
dlya odnorodnyh struktur. Takim
obrazom, metod uslovnoi koncentracii yavlyaetsya moshnym instrumentom
poiska granicy perehoda ot rezhima fraktal'noi klasterizacii k
odnorodnosti.
Vyshe my rassmotreli fraktal'nye stohasticheskie processy dlya chastic
odnogo sorta. Real'nye galaktiki imeyut funkciyu svetimosti 
, obychno zadavaemuyu zakonom Shehtera
opisyvayushim dolyu galaktik so svetimostyami v intervale
. Zdes' 
i 
- parametry, opredelyaemye iz nablyudenii, 
- postoyannaya normirovki, takaya chto
, poetomu
gde
- nepolnaya gamma-funkciya; 
-
parametr obrezaniya funkcii svetimosti so storony malyh znachenii.
Stohasticheskie processy, v kotoryh fraktal'nye nositeli (polozheniya
chastic) harakterizuyutsya razlichnymi znacheniyami nekotoroi sluchainoi
velichiny 
(naprimer, svetimosti 
ili massy 
), otnosyatsya
k klassu mul'tifraktal'nyh processov. Rassmotrim realizaciyu takogo
stohasticheskogo processa, kotoraya harakterizuetsya sleduyushei
realizovannoi plotnost'yu svetimosti (massy):
V takom sluchae funkciya plotnosti (svetimosti, massy) galaktik yavlyaetsya mul'tifraktal'noi meroi na mnozhestve realizacii. Mul'tifraktaly harakterizuyutsya spektrom fraktal'nyh razmernostei
v zavisimosti ot svetimosti (massy) galaktik.
Pust'
- chislo galaktik so
svetimostyami v intervale
v sfericheskoi
obolochke
s centrom v tochke
, prinadlezhashei strukture. Obobshaya ponyatie uslovnoi
koncentracii (5) odinakovyh chastic na sluchai chastic,
harakterizuyushihsya raznymi znacheniyami svetimosti (massy), vvedem
uslovnuyu plotnost' svetimosti (massy) galaktik v vide
Mozhno pokazat', chto dlya shirokogo klassa mul'tifraktal'nyh stohasticheskih processov uslovnuyu plotnost' svetimosti mozhno predstavit' v vide
Pri etom shehterovskii vid funkcii svetimosti poluchaetsya kak sledstvie mul'tifraktal'nosti, a ne kak dopolnitel'noe predpolozhenie. Osobennost'yu vyrazheniya (12) yavlyaetsya zavisimost' parametra izloma funkcii svetimosti ot radiusa oblasti
, a takzhe zavisimost' fraktal'noi razmernosti ot
svetimosti galaktik . Eti osobennosti mogut
ispol'zovat'sya kak testy mul'tifraktal'nosti, no trebuyut bol'shih
ob'emov vyborok, tak kak fraktal'nyi analiz nado provodit' dlya
kazhdogo intervala svetimostei.
<< 2. Nablyudatel'nye dannye | Oglavlenie | 4. Metody analiza struktury >>
|
Publikacii s klyuchevymi slovami:
krupnomasshtabnaya struktura Vselennoi
Publikacii so slovami: krupnomasshtabnaya struktura Vselennoi | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
