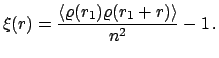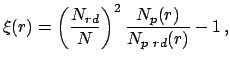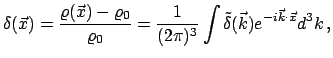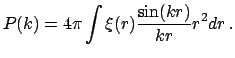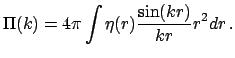<< 3. Sposoby opisaniya struktury | Oglavlenie | 5. Sovremennoe sostoyanie >>

4. Metody analiza struktury

Na praktike pri izuchenii svoistv krupnomasshtabnoi struktury procedura analiza katalogov okazyvaetsya dostatochno slozhnoi. Sobstvenno analizu struktury dolzhen predshestvovat' vybor opredelennoi kosmologicheskoi modeli, poluchenie absolyutnyh velichin galaktik s uchetom K-popravki, poglosheniya sveta, effektov evolyucii i pr., uchet «geometricheskih» osobennostei kataloga (formy oblasti, ohvachennoi katalogom na nebesnoi sfere i kraevyh effektov), vydelenie dostatochno polnyh po svetimosti vyborok galaktik, ogranichennyh po razmeru. Tol'ko posle etogo mozhno pristupat' k vydeleniyu struktury.

Naibolee rasprostranennym podhodom k analizu krupnomasshtabnoi struktury Vselennoi yavlyaetsya metod korrelyacionnyh funkcii.

Korrelyacionnaya funkciya opredelyaetsya kak mera veroyatnosti otkloneniya raspredeleniya chastic ot puassonovskogo odnorodnogo raspredeleniya na rasstoyanii ot nekotoroi fiksirovannoi chasticy iz dannoi vyborki. Dlya opredeleniya dvuhtochechnoi korrelyacionnoi funkcii neobhodimo rassmotret' dve beskonechno malye sfery v tochkah i s ob'emami i , togda sovmestnaya veroyatnost' naiti odnovremenno ob'ekty v sferah, rasstoyanie mezhdu kotorymi ravno , budet

gde est' srednyaya koncentraciya chastic, kotoraya ne zavisit ot polozheniya tochki i velichiny ob'ema. Esli dlya opisaniya raspredeleniya chastic ispol'zuetsya nepreryvnaya funkciya plotnosti , srednee znachenie kotoroi , to dvuhtochechnaya korrelyacionnaya funkciya sovpadaet s bezrazmernoi avtokorrelyacionnoi funkciei sluchainogo processa :

Dlya polucheniya ocenki , sootvetstvuyushei dannoi vyborke ob'ektov, ispol'zuyut razlichnye statistiki, sredi kotoryh standartnoi schitaetsya sleduyushaya:

gde  - chislo par ob'ektov v kataloge s rasstoyaniyami v intervale ,  - chislo par chastic s takimi zhe vzaimnymi rasstoyaniyami, naidennymi dlya sluchaya odnorodnogo stohasticheskogo tochechnogo processa, zapolnyayushego tot zhe ob'em, i  - polnoe chislo ob'ektov v vyborke i v sluchainom raspredelenii sootvetstvenno.

Naibolee sushestvennym predpolozheniem, lezhashim v osnove opredeleniya korrelyacionnoi funkcii, yavlyaetsya uslovie apriornogo sushestvovaniya srednei plotnosti chisla ob'ektov, kotoraya ne zavisit ot velichiny rassmatrivaemogo ob'ema. V chastnosti, eto predpolozhenie pozvolyaet ispol'zovat' beskonechno malye ob'emy v formule (13).

Esli prostranstvennoe raspredelenie ob'ektov harakterizuetsya nekotoroi sluchainoi funkciei plotnosti, to fluktuacii etoi funkcii mozhno predstavit' v vide integrala Fur'e kak superpoziciyu ploskih prostranstvennyh voln

gde Fur'e-obraz raspredeleniya plotnosti yavlyaetsya kompleksnoi velichinoi i, sledovatel'no, mozhet byt' predstavlen v vide

Takim obrazom, polnoe opisanie prostranstvennogo raspredeleniya plotnosti ob'ektov dolzhno vklyuchat' rassmotrenie kak spektra amplitud , tak i spektra faz .

V sluchae gaussovyh sluchainyh processov fazy ploskih voln raspredeleny ravnomerno v intervale i dlya harakteristiki polya plotnosti dostatochno rassmatrivat' tol'ko spektr moshnosti

V sluchae izotropnyh raspredelenii spektr moshnosti i korrelyacionnaya funkciya svyazany sootnosheniem

Tak chto dlya stepennoi korrelyacionnoi funkcii spektr moshnosti imeet tozhe stepennoi vid .

Bol'shinstvo rabot, posvyashennyh analizu krupnomasshtabnoi struktury, ispol'zuyut tol'ko spektr moshnosti , hotya fazovyi spektr neset v sebe vazhnuyu dopolnitel'nuyu informaciyu o negaussovosti processa klasterizacii ob'ektov.

Dlya stohasticheskih fraktal'nyh processov takzhe mozhno provesti Fur'e-analiz funkcii plotnosti. Mozhno vvesti ponyatie masshtabno nezavisimogo (obobshennogo) spektra moshnosti fraktal'nyh processov , kotoryi opredelyaetsya vyrazheniem, analogichnym (19), gde vmesto pod integralom stoit uslovnaya plotnost' (5), tak chto

V sluchae stohasticheskih fraktal'nyh processov obobshennyi spektr moshnosti imeet stepennoi vid , gde - fraktal'naya razmernost'.

Topologiya raspredeleniya predstavlyaet soboi statistiku, opredelyayushuyu tak nazyvaemyi «rod poverhnosti». Dannaya statistika provoditsya po sglazhennomu tochechnomu raspredeleniyu, kotoroe poluchaetsya pri postroenii poverhnostei odinakovoi plotnosti. Pri etom issleduemyi ob'em razdelyaetsya na oblasti ponizhennoi i povyshennoi plotnosti gladkimi poverhnostyami.

Rod poverhnosti opredelyaetsya kak

gde  - kolichestvo «dyrok» v poluchivsheisya figure;  - kolichestvo izolirovannyh oblastei.

Dlya sfery , dlya izolirovannyh sfer , dlya tora . Voobshe raven maksimal'nomu kolichestvu principial'no razlichnyh razrezov poverhnosti, kotorye mozhno sdelat', sohraniv celostnost' tela.

Minimal'noe ohvatyvayushee derevo - odin iz sposobov vyyavleniya klasterizacii ob'ektov. Na ob'ektah vyborki stroitsya graf (mozhno pokazat', chto poluchayushiisya v rezul'tate graf edinstvenen, poetomu nachinat' postroenie mozhno s lyubogo ob'ekta vyborki). Na nekotorom shage proishodit poisk ob'ekta, nahodyashegosya na naimen'shem rasstoyanii ot kakogo-libo ob'ekta, uzhe prisoedinennogo k grafu. Eti dva ob'ekta soedinyayutsya rebrom. Dalee process povtoryaetsya, poka vse ob'ekty vyborki ne budut prisoedineny k grafu. Posle postroeniya grafa imeyutsya dannye o dlinah reber, soedinyayushih ob'ekty, i o kolichestve reber, prisoedinennyh k kazhdoi vershine grafa. Ispol'zuya eti dannye, mozhno vydelyat' ob'ekty, nahodyashiesya v oblastyah povyshennoi i ponizhennoi plotnosti.

Perkolyaciya - odin iz metodov klasternogo analiza, ispol'zuetsya dlya ob'edineniya oblastei povyshennoi plotnosti. Vokrug ob'ekta, vybrannogo nachal'nym, opisyvaetsya sfera nekotorogo radiusa (perkolyacionnyi radius - edinstvennyi zadavaemyi parametr etogo metoda). Esli v sferu popadayut ob'ekty, vokrug nih tozhe opisyvayutsya sfery togo zhe radiusa, i tak dalee, poka ni v odnu sferu ne popadet ni odin novyi ob'ekt. Dalee vybirayutsya novye ob'ekty, ne voshedshie v klastery, poluchennye ranee. Potom mozhno naiti centry mass klasterov i otmetit' ih kak novye ob'ekty. Takim obrazom, naprimer, sozdavalsya izvestnyi katalog sverhskoplenii Einasto.

Sushestvuyut takzhe kak mnogochislennye modifikacii perechislennyh metodov, tak i menee rasprostranennye statistiki, ispol'zuemye dlya izucheniya raspredeleniya astrofizicheskih ob'ektov. Naprimer, bolee detal'noe postroenie trehmernoi kartiny blizhaishih oblastei Vselennoi posluzhilo tolchkom k razvitiyu raznoobraznyh statisticheskih metodov vydeleniya i issledovaniya razlichnyh struktur v raspredelenii ob'ektov vo Vselennoi - «pustot» (voids), «cepochek» (filaments), sverhskoplenii («sten», sostoyashih iz galaktik). V otlichie, naprimer, ot dvuhtochechnoi korrelyacionnoi funkcii eti metody bolee tonko vydelyayut morfologicheskie osobennosti struktur.

---

<< 3. Sposoby opisaniya struktury | Oglavlenie | 5. Sovremennoe sostoyanie >>

Publikacii s klyuchevymi slovami: krupnomasshtabnaya struktura Vselennoi Publikacii so slovami: krupnomasshtabnaya struktura Vselennoi
Sm. takzhe: Million galaktik Voidy Blizhnyaya Vselennaya Samaya krupnaya struktura vo Vselennoi. Nasha Galaktika v obzore 2MASS Eshe o blinnoi teorii ... Kusok iskusstvennoi Vselennoi Vse publikacii na tu zhe temu >>