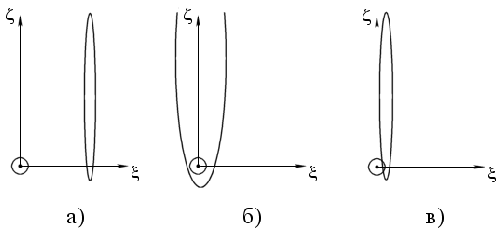<< 2. Asteroidy, sblizhayushiesya s | Oglavlenie | 4. Turinskaya i Palermskaya >>
3. Poisk potencial'no opasnyh sblizhenii asteroidov s Zemlei i ocenka veroyatnosti stolknovenii
Rassmotrim nekotorye ispol'zuemye v reshenii problemy asteroidnoi opasnosti velichiny i opredeleniya.
Minimal'noe rasstoyanie mezhdu orbitami - parametr MOID.
Velichina minimal'nogo rasstoyaniya mezhdu orbitoi ASZ i orbitoi Zemli
(parametr 
- Minimum Orbital Intersection Distance) sluzhit
kriteriem dlya vydeleniya potencial'no opasnyh asteroidov iz chisla
vseh ASZ.
Minimal'noe rasstoyanie mezhdu dvumya orbitami dostigaetsya vdol' nekotoroi pryamoi, kotoraya perpendikulyarna k orbitam oboih tel, to est' perpendikulyarna k kasatel'nym, provedennym k orbitam v tochkah, nahodyashihsya na minimal'nom dlya dannyh orbit rasstoyanii. Tochki dvuh sofokusnyh orbit, nahodyashiesya na minimal'nom rasstoyanii, i velichina samogo rasstoyaniya mogut byt' naideny analiticheski ili chislennym sposobom. V obshem sluchae zadacha svoditsya k resheniyu trigonometricheskogo uravneniya vos'moi stepeni (Kholshevnikov and Vassiliev, 1999).
Skorost' soudareniya tela s Zemlei.
Oboznachim vektor geliocentricheskoi skorosti asteroida
v moment stolknoveniya kak v s komponentami 
, 
, 
,
a vektor geliocentricheskoi skorosti Zemli v etot moment kak
. V takom sluchae skorost' tela
otnositel'no Zemli bez ucheta ee prityazheniya ravna
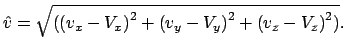
Etu skorost' otnositel'no Zemli, eshe ne izmenennuyu ee prityazheniem, chasto nazyvayut giperbolicheskim izbytkom skorosti. Polnaya skorost' soudareniya s Zemlei nahoditsya po formule
|
(1) |
gde
- parabolicheskaya skorost'
otnositel'no Zemli, to est' skorost', kotoruyu priobretaet telo,
padayushee na Zemlyu «iz beskonechnosti», gde ego skorost'
otnositel'no Zemli ravna nulyu. Parabolicheskaya skorost'
otnositel'no Zemli priblizhenno ravna 11.18 km/s.
Otmetim, chto srednie skorosti stolknoveniya ASZ s Zemlei (s uchetom prityazheniya Zemli) sostavlyayut okolo 20 km/s (Kholshevnikov and Shor, 1995; 1996; Gladman et al., 2000).
Energiya stolknoveniya. Pri stolknovenii kosmicheskogo tela s Zemlei ego kineticheskaya energiya yavlyaetsya glavnym razrushitel'nym faktorom. Poetomu ocenka kineticheskoi energii yavlyaetsya edva li ne perveishei zadachei pri obnaruzhenii tela na orbite, privodyashei k stolknoveniyu s Zemlei.
Kineticheskaya energiya 
vyrazhaetsya formuloi
, v kotoroi 
- massa tela, a
- ego skorost' otnositel'no Zemli s uchetom
prityazheniya Zemli, rasschitannaya po formule (1).
Skorost' tela otnositel'no Zemli vsegda mozhet byt' vychislena dostatochno tochno dlya orientirovochnyh raschetov, a massu, za otsutstviem drugih vozmozhnostei, v podavlyayushem chisle sluchaev massu mozhno ocenit' po fotometricheskomu diametru tela i ego predpolagaemoi plotnosti.
Velichinu kineticheskoi energii, prinosimoi padayushim na Zemlyu telom,
prinyato vyrazhat' v megatonnah trinitrotoluolovogo ekvivalenta. Pri
etom
Ploskost' celi.
Ploskost' celi - eto ploskost', prohodyashaya cherez centr
planety-misheni perpendikulyarno k nevozmushennomu
vektoru skorosti tela-snaryada otnositel'no planety-misheni 
.
Pricel'noe rasstoyanie i radius zahvata. Otnositel'naya
skorost' asteroida na vhode v sferu deistviya ravna
raznosti geliocentricheskih skorostei asteroida i Zemli. Po
napravleniyu ona blizka k asimptote giperboly, opisyvaemoi telom v
sfere deistviya planety. Obognuv Zemlyu, na vyhode iz sfery deistviya
asteroid imeet tu zhe samuyu po velichine otnositel'nuyu skorost'
, no ee napravlenie izmenyaetsya na nekotoryi ugol.
Rasstoyanie ot centra Zemli do etoi asimptoty nazyvaetsya pricel'nym
rasstoyaniem (
). Pricel'noe rasstoyanie svyazano s minimal'noe
rasstoyaniem giperboly ot centra Zemli (
) sleduyushim
sootnosheniem:
|
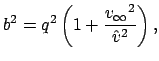
(2) |
gde
est' parabolicheskaya skorost' otnositel'no Zemli. V etoi
formule 
- gravitacionnaya postoyannaya, 
- massa
Zemli, a 
- ee ekvatorial'nyi radius. Esli v formulu
(2) podstavit' , ravnoe , to budet ravno
pricel'nomu rasstoyaniyu, pri kotorom traektoriya asteroida kosnetsya
poverhnosti Zemli. Sootvetstvuyushee znachenie pricel'nogo rasstoyaniya
nazyvaetsya radiusom zahvata. Pri reshenii voprosa o real'nosti
stolknoveniya sleduet ispol'zovat' ne radius Zemli, a ee radius
zahvata.
Na pervom etape resheniya zadachi ob ocenke veroyatnosti
stolknoveniya ASZ s Zemlei stroitsya nominal'naya orbita asteroida,
poluchennaya putem uluchsheniya predvaritel'noi orbity iz nablyudenii s
pomosh'yu metoda naimen'shih kvadratov (MNK). Pri etom elementy
nominal'noi orbity opredelyayutsya so srednekvadratichnymi oshibkami
. Takim obrazom, v prostranstve elementov orbit
nominal'naya orbita okruzhena oblast'yu vozmozhnyh orbit. Eta
oblast' mozhet byt' kvalificirovana kak oblast' neopredelennosti
nachal'nyh uslovii dvizheniya. Fakticheskaya orbita tela, kotoraya
nam neizvestna, nahoditsya gde-to vnutri oblasti
neopredelennosti. Ellipsoid s centrom v tochke na nominal'noi
orbite i poluosyami, ravnymi 
, ogranichivaet oblast', v
kotoroi sosredotocheny prakticheski vse sovmestimye s nablyudeniyami
nachal'nye usloviya. My budem nazyvat' takoi ellipsoid
doveritel'nym, a ogranichivaemuyu im oblast' nachal'nyh uslovii -
doveritel'noi oblast'yu. Telo na vozmozhnoi orbite my budem nazyvat'
virtual'nym (vozmozhnym) asteroidom (Milani et al., 2000).
Na vtorom etape budem predpolagat', chto zadacha imeet lineinyi harakter. Eto ravnosil'no predpolozheniyu, chto oblast' prostranstva, zanyataya virtual'nymi asteroidami v okrestnosti sblizheniya asteroida, sootvetstvuyushego nominal'nomu resheniyu, s Zemlei, predstavlyaet soboi ellipsoid.
Rassmotrim sistemu koordinat, svyazannuyu s ploskost'yu celi.
Os' 
napravlena parallel'no skorosti asteroida otnositel'no Zemli na
granice sfery deistviya (), os' 
vdol' kratchaishego rasstoyaniya
mezhdu orbitami, os' 
perpendikulyarna osyam i i
napravlena tak, chto vmeste s nimi obrazuet pravuyu sistemu koordinat.
Cepochka virtual'nyh asteroidov, vytyanuvshihsya vdol' nominal'noi
orbity, proektiruetsya na ploskost' celi v pryamuyu, parallel'nuyu osi
, prichem virtual'nyi asteroid, sootvetstvuyushii centru
doveritel'nogo ellipsoida v moment 
, peresekaet ploskost'
celi v tochke, raspolozhennoi, voobshe govorya, vyshe ili nizhe osi
. Oblast' vokrug etoi tochki na ploskosti ,
yavlyaetsya otobrazheniem oblasti vozmozhnyh nachal'nyh uslovii dvizheniya
na ploskost' celi. Poskol'ku my predpolagaem lineinyi harakter
zadachi, mozhno utverzhdat', chto oblast' nachal'nyh znachenii,
ogranichennaya v moment doveritel'nym ellipsoidom, otobrazitsya
na ploskost' , v chast' ploskosti, ogranichennuyu
ellipsom s centrom v tochke, sootvetstvuyushei centru doveritel'nogo
ellipsoida. Zadacha svoditsya k tomu, chtoby naiti
koordinaty centra ellipsa na ploskosti , i ego
poluosi i ocenit' raspolozhenie ellipsa otnositel'no izobrazheniya
Zemli.
Vozmozhny sleduyushie tri sluchaya vzaimnogo raspolozheniya Zemli i ellipsa na ploskosti celi:
- ellips raspolozhen na nekotorom rasstoyanii ot okruzhnosti s radiusom, ravnym radiusu zahvata Zemli (ris. 2,a), chto prakticheski isklyuchaet vozmozhnost' stolknoveniya asteroida s Zemlei;
- kruzhok s radiusom, ravnym radiusu zahvata, nahoditsya vnutri ellipsa (ris. 2,b). Veroyatnost' stolknoveniya mozhet byt' rasschitana, ishodya iz otnosheniya ploshadi kruzhka k ploshadi, ogranichennoi ellipsom. Dlya povysheniya tochnosti prognoza mozhno uchest' neodinakovuyu veroyatnost' popadaniya virtual'nyh asteroidov v razlichnye tochki oblasti, ogranichennoi ellipsom;
- ploshad', ogranichennaya ellipsom, chastichno pokryvaet oblast' zahvata Zemli (ris. 2,v). Etot sluchai prakticheski ne otlichaetsya ot predydushego. Veroyatnost' stolknoveniya rasschityvaetsya s uchetom otnosheniya perekryvayusheisya oblasti ko vsei ploshadi, ogranichennoi ellipsom.
Nelineinyi harakter zadacha mozhet imet' mesto po mnogim prichinam.
Doveritel'nyi ellipsoid uzhe v moment mozhet nedostatochno
horosho opisyvat' oblast' vozmozhnyh nachal'nyh uslovii, poskol'ku
samo raspredelenie oshibok nablyudenii mozhet ne podchinyat'sya zakonu
Gaussa. Proekciya doveritel'nogo ellipsoida na ploskost' celi v
moment 
sblizheniya s Zemlei, otdalennyi ot na desyatiletiya,
vytyagivaetsya v ochen' uzkuyu oblast', kotoraya k tomu zhe iskrivlyaetsya
v sootvetstvii s kriviznoi zemnoi orbity. Po vsem etim prichinam
lineinyi analiz zadachi stanovitsya neadekvatnym, i trebuetsya
primenenie bolee tonkih metodov analiza. K nastoyashemu vremeni
predlozheno dva takih metoda: metod Monte-Karlo i metod linii
variacii.
Poluchenie ocenki veroyatnosti stolknoveniya ASZ s Zemlei v sluchae nelineinoi zadachi imeet svoi osobennosti, kotorye, vvidu ih slozhnosti, privodit' zdes' ne budem.
<< 2. Asteroidy, sblizhayushiesya s | Oglavlenie | 4. Turinskaya i Palermskaya >>
|
Publikacii s klyuchevymi slovami:
asteroidy - komety - asteroidnaya opasnost' - stolknoveniya - Turinskaya shkala
Publikacii so slovami: asteroidy - komety - asteroidnaya opasnost' - stolknoveniya - Turinskaya shkala | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
