po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu

Astronet | Kartinka dnya | Obzory astro-ph | Novosti | Stat'i | Knigi | Karta neba | Sozvezdiya | Peremennye Zvezdy | A&ATr | Glossarii

planeta Astronet | Fizika kosmosa | Biografii | Slovar' | Klyuchevye slova | Astronomiya v Rossii | Forumy | Seminary | Sverhnovye

ChETVERTAYa VSEROSSI'SKAYa OTKRYTAYa ZAOChNAYa
ShKOL'NAYa ASTRONOMIChESKAYa OLIMPIADA
ZADAChI S REShENIYaMI

1. Uslovie. Iskusstvennyi sputnik Zemli obrashaetsya vokrug nashei planety po krugovoi orbite, lezhashei v ploskosti ekliptiki. Pri nablyudenii iz Krasnodara etot sputnik i tochka vesennego ravnodenstviya vsegda voshodyat nad gorizontom strogo odnovremenno. V opredelennye momenty vremeni sputnik okazyvaetsya na nebe tochno nad tochkoi yuga. Na kakoi vysote nad gorizontom on v eto vremya nahoditsya? Chemu raven radius orbity sputnika? Refrakciei i sutochnym parallaksom sputnika prenebrech'.

 

1. Reshenie. V lyubom meste Zemli, krome polyusov, tochka vesennego ravnodenstviya voshodit rovno cherez odni zvezdnye sutki (okolo 23 chasov 56 minut) posle predydushego voshoda. Sledovatel'no, voshody iskusstvennogo sputnika takzhe otstoyat drug ot druga na odni zvezdnye sutki. Tak kak my ne uchityvaem sutochnoe parallakticheskoe smeshenie sputnika, on vsegda budet nahodit'sya na ekliptike. Na shirote Krasnodara (+45œ) ekliptika ne mozhet sovpadat' s gorizontom i, yavlyayas' bol'shim krugom nebesnoi sfery, peresekaet gorizont v dvuh protivopolozhnyh tochkah. Odna iz nih - voshodyashaya v etot moment tochka vesennego ravnodenstviya, vtoraya - tochka osennego ravnodenstviya. Takim obrazom, v moment svoego voshoda iskusstvennyi sputnik Zemli nahodilsya v odnoi iz etih dvuh tochek. Po proshestvii odnih zvezdnyh sutok sputnik budet voshodit' v toi zhe tochke neba. V protivopolozhnoi tochke krugovoi orbity on by ne voshodil, a zahodil za gorizont, tak kak v lyuboi moment vremeni nad gorizontom raspolagaetsya rovno polovina orbity sputnika.

Ochevidno, chto sputnik, vrashayas' vokrug Zemli, ne mozhet byt' nepodvizhnym otnositel'no zvezd. Rassmotrim sluchai, pri kotoryh iskusstvennyi sputnik Zemli, odin raz voshodya i zahodya za gorizont, vozvrashaetsya v tu zhe tochku neba po proshestvii zvezdnyh sutok. Eto, v chastnosti, mozhet byt', esli period obrasheniya sputnika raven zvezdnym sutkam, a napravlenie sovpadaet s napravleniem vrasheniya Zemli. Takaya orbita pohozha na geostacionarnuyu, no tak kak sputnik vrashaetsya ne v ploskosti ekvatora, a v ploskosti ekliptiki, na zemnom nebe on budet opisyvat' uzkuyu razmerom okolo 47œ. Esli pri etom on okazhetsya v tochke vesennego ravnodenstviya v moment ee voshoda, to on i sam budet voshodit' v eto zhe vremya na vostoke kazhdye zvezdnye sutki (sm. risunok).

 

 

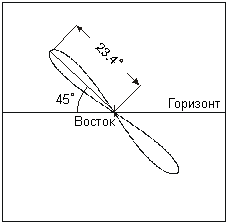
Odnako dannaya kartina protivorechit usloviyu zadachi - iz risunka mozhno ubedit'sya, chto sputnik vsegda budet nahodit'sya v vostochnoi chasti neba i nikogda ne okazhetsya nad yuzhnym gorizontom. Nam neobhodimo rassmotret' eshe odin vozmozhnyi variant, pri kotorom sputnik za odni sutki zavershaet oborot po nebu otnositel'no zemnogo nablyudatelya, odin raz voshodya i zahodya za gorizont. Oboznachim sinodicheskii period obrasheniya sputnika cherez S, sidericheskii (zvezdnyi) period ego obrasheniya cherez T, a prodolzhitel'nost' zvezdnyh sutok cherez T₀. Eti tri velichiny svyazany sootnosheniem

 

 

Znak <+> pered velichinami (1/S) i (1/T) sootvetstvuet vrasheniyu sputnika otnositel'no nablyudatelya i otnositel'no centra Zemli v napravlenii, sovpadayushem s napravleniem vrasheniya Zemli, a znak <-> sootvetstvuet protivopolozhnomu napravleniyu. Tak kak velichiny S i T₀ ravny drug drugu, znak <-> pered velichinoi (1/S) stoyat' ne mozhet, inache velichina T obratitsya v beskonechnost'. Tak kak velichina S polozhitel'na, reshenie budet sushestvovat' tol'ko pri odnoi kombinacii znakov:

 

 

iz chego my poluchaem, chto sidericheskii period obrasheniya sputnika T raven polovine zvezdnyh sutok, to est' 11 chasam 58 minutam. Sputnik vrashaetsya v odnom napravlenii s Zemlei, no s vdvoe bol'shei uglovoi skorost'yu, poetomu on, kak Fobos na Marse, budet voshodit' na zapade i zahodit' na vostoke. Vo vremya svoego voshoda sputnik budet nahodit'sya v tochke osennego ravnodenstviya, kotoraya sama pri etom budet zahodit' za gorizont. Peremeshayas' s zapada na vostok, sputnik budet dvigat'sya navstrechu tochke vesennego ravnodenstviya, vzoshedshei odnovremenno s nim v protivopolozhnoi tochke neba (sm. vtoroi risunok). Cherez 5 chasov 59 minut posle voshoda sputnik sdelaet polovinu sidericheskogo oborota vokrug Zemli i okazhetsya v tochke vesennego ravnodenstviya, kotoraya pri etom budet kul'minirovat' nad yuzhnym gorizontom na vysote 45œ. My poluchili otvet na pervyi vopros zadachi.

 

 

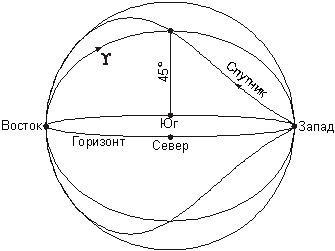
Dlya otveta na vtoroi vopros dostatochno vospol'zovat'sya obobshennym III zakonom Keplera. Radius orbity raven

 

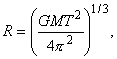
chto sostavlyaet 26.6 tysyach kilometrov (M - massa Zemli).

 

 

2. Uslovie. Iskusstvennyi sputnik Zemli obrashaetsya vokrug nashei planety po ellipticheskoi orbite, lezhashei v ploskosti ekliptiki. V perigee on nahoditsya na tom zhe rasstoyanii ot Zemli, chto i Luna. Ocenite maksimal'no vozmozhnyi ekscentrisitet orbity sputnika. Gravitacionnoe vliyanie Luny ne uchityvat'.

 

2. Reshenie. Vozmozhnoe znachenie ekscentrisiteta orbity sputnika ogranicheno sverhu prilivnym vliyaniem Solnca (vliyanie Luny, po usloviyu zadachi, v raschet ne beretsya). Esli v tochke apogeya orbity sputnik podoidet k vnutrennei tochke Lagranzha sistemy Solnce-Zemlya, orbita sputnika stanet neustoichivoi, i on pereidet na geliocentricheskuyu orbitu, stav iskusstvennoi planetoi Solnechnoi sistemy. Rassmotrim naibolee kriticheskii dlya ustoichivosti orbity sluchai, kogda v apogee sputnik okazyvaetsya mezhdu Solncem i Zemlei (sm. risunok). Tak kak orbita sputnika lezhit v ploskosti ekliptiki, to podobnaya situaciya obyazatel'no realizuetsya odin raz v god.

 

 

Oboznachim perigeinoe i apogeinoe rasstoyanie do sputnika sootvetstvenno kak p i a, rasstoyanie ot Solnca do Zemli - cherez R. Predpolozhim, chto v tochke apogeya sputnik okazalsya vo vnutrennei tochke Lagranzha. Eta tochka mozhet dvigat'sya vokrug Solnca s toi zhe uglovoi skorost'yu w, chto i Zemlya. Zapishem uravneniya vrasheniya tochki Lagranzha i Zemli:

 

 

Uchityvaya, chto velichina a znachitel'no men'she, chem R, mozhno zapisat'

 

 

Vyrazhaya velichinu w iz uravneniya vrasheniya Zemli, poluchaem

 

 

Iz poslednego sootnosheniya poluchaem ocenku maksimal'nogo znacheniya apogeinogo rasstoyaniya

 

 

i ekscentrisiteta orbity sputnika (s uchetom izvestnogo znacheniya p, ravnogo 384 tysyacham kilometrov):

 

 

 

 

Ekscentrisitet pri etom poluchaetsya ravnym 0.633. Uchityvaya ocenochnyi harakter zadachi, takoi podhod vpolne logichen i pri pravil'nyh vychisleniyah vpolne mozhet byt' ocenen v 6 ballov. Ostal'nye podhody ocenivayutsya men'shim kolichestvom ballov v zavisimosti ot ih pravdopodobnosti.

 

3. Uslovie. Dalekaya zvezda nahoditsya na nebe v tochke letnego solncestoyaniya. Vo vremya prohozhdeniya mimo zvezdy voshodyashego uzla lunnoi orbity na Zemle v kazhdyi oborot Luny budet nablyudat'sya pokrytie dannoi zvezdy Lunoi. Skol'ko pokrytii budet soderzhat' seriya? Na kakoi shirote i v kakoi chasti neba budet vidno pervoe i poslednee pokrytie zvezdy Lunoi v serii? Orbitu Luny schitat' krugovoi.

 

3. Reshenie. Esli by Luna obrashalas' vokrug Zemli tochno v ploskosti ekliptiki, to ona pokryvala by zvezdu v tochke letnego solncestoyaniya v svoi kazhdyi oborot vokrug Zemli, prichem eto pokrytie bylo by vidno v ekvatorial'nom i severnom tropicheskom poyasah nashei planety. Na samom dele ploskost' orbity Luny naklonena k ploskosti ekliptiki na ugol i, ravnyi 5.15œ, chto okazyvaetsya dostatochnym dlya togo, chtoby v bol'shinstve sluchaev Luna proshla na nebe vyshe ili nizhe zvezdy, i pokrytie ne nastupilo. Dlya togo, chtoby ono vse zhe sluchilos', Luna, prohodya na nebe mimo zvezdy, dolzhna nahodit'sya vblizi odnogo iz dvuh uzlov svoei orbity, v kotoryh ona peresekaet ploskost' ekliptiki.

Sidericheskii (zvezdnyi) period obrasheniya Luny T_S sostavlyaet 27.321662 sutok, a drakonicheskii period T_D (period vozvrasheniya k tomu zhe uzlu orbity) nemnogo koroche - 27.212220 sutok. Zavershaya svoi oborot otnositel'no zvezd, Luna sovershit 1.00402 drakonicheskih oborota, i esli odno pokrytie proizoshlo tochno v voshodyashem uzle lunnoi orbity, to sleduyushee proizoidet uzhe posle prohozhdeniya etogo uzla, pri etom Luna okazhetsya chut' vyshe, i oblast' vidimosti pokrytiya na Zemle smestitsya na sever (sm. risunok).

 

 

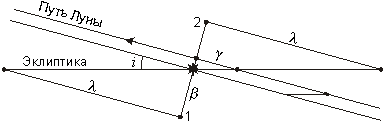
Uglovoe rasstoyanie mezhdu Lunoi i uzlom orbity sostavit

 

 

Smeshayas' na takuyu velichinu kazhdyi sidericheskii mesyac, liniya uzlov lunnoi orbity sdelaet polnyi oborot za 248.65 sidericheskih mesyacev, to est' za 18.6 let. Za etot period nastupyat dve epohi pokrytii Lunoi zvezdy vblizi ekliptiki - vo vremya prohozhdeniya voshodyashego i nishodyashego uzla orbity vblizi zvezdy. Dlya zvezdy, nahodyasheisya tochno na ekliptike, eti serii budut otstoyat' na 9.3 goda drug ot druga. V zadache trebuetsya naiti prodolzhitel'nost' odnoi serii. Dlya etogo nuzhno opredelit', na kakom maksimal'nom udalenii ot uzla orbity Luny mozhet proizoiti pokrytie.

 

 

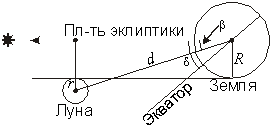
Na vtorom risunke pokazana predel'naya situaciya, pri kotoroi kasatel'noe pokrytie zvezdy Lunoi vidno tol'ko v odnoi tochke Zemli. Maksimal'noe uglovoe rasstoyanie Luny ot ekliptiki v etom sluchae sostavlyaet

 

 

Zdes', po usloviyu zadachi, my prinimaem orbitu Luny krugovoi s radiusom d, ravnomu 384.4 tysyach km, R i r - radiusy Zemli i Luny. Vozvrashayas' k pervomu risunku, vychislyaem maksimal'noe rasstoyanie ot Luny do uzla orbity vo vremya pokrytiya:

 

l=bctg i=13.41œ.

 

Srednee kolichestvo pokrytii v odnoi serii, kak vidno iz pervogo risunka, budet ravno

 

 

Real'noe chislo pokrytii primerno s odinakovoi veroyatnost'yu budet ravno 18 ili 19. Prodolzhitel'nost' serii sostavit 17 ili 18 sidericheskih periodov obrasheniya Luny, to est' 1.27 ili 1.35 goda.

Pervoe pokrytie zvezdy Lunoi v sluchae voshodyashego uzla proizoidet vblizi polozheniya 1 na pervom risunke, ta zhe situaciya izobrazhena na vtorom risunke. Luna zadenet zvezdu svoim severnym kraem, i eto pokrytie budet vidno v yuzhnom polusharii Zemli. Luna budet nahodit'sya na severnom gorizonte (tochnee, v 5.15œ vdol' gorizonta k zapadu ot tochki severa), sklonenie zvezdy d sostavlyaet +23.4œ, i pokrytie budet nablyudat'sya vblizi Yuzhnogo Polyarnogo Kruga. Poslednee pokrytie serii (polozhenie 2 na pervom risunke) budet vidno vblizi Severnogo Polyarnogo Kruga v 5.15œ k vostoku ot tochki severa vdol' gorizonta.

 

 

4. Uslovie. Polosa vidimosti polnogo solnechnogo zatmeniya proshla poocheredno po gorodam: Oslo (Norvegiya), Varshava (Pol'sha), Konstanca (Rumyniya), Ankara (Turciya), Bagdad (Irak), Kerman (Iran) i Islamabad (Pakistan). V kakom iz chetyreh astronomicheskih sezonov goda proizoshlo dannoe zatmenie?

 

4. Reshenie. V tablice privedeny koordinaty perechislennyh v uslovii gorodov.

 

 

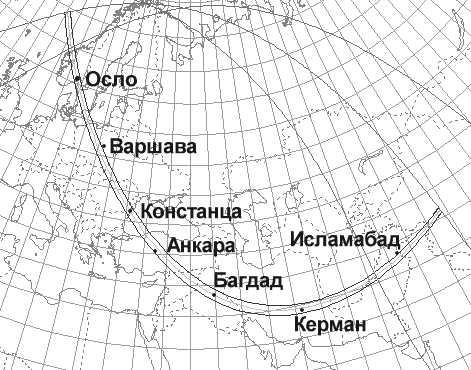
Iz tablicy vidno, chto ten' bol'shuyu chast' vremeni dvigalas' na yugo-vostok, i lish' v konce ona stala dvigat'sya na vostok, a zatem dazhe povernula k severo-vostoku. Vidimyi put' teni po poverhnosti Zemli pokazan na karte.

 

 

Rassmotrim, kak mogla by dvigat'sya ten' Luny po umerennym i tropicheskim shirotam severnogo polushariya v seredine chetyreh astronomicheskih sezonov goda (napominaem, chto nachalom sezona schitaetsya moment ravnodenstviya ili solncestoyaniya). Na risunke dlya kazhdogo iz chetyreh sluchaev pokazan vid Zemli i polosy teni so storony Solnca i Luny. Lunnaya ten' dvizhetsya na risunke sleva napravo, v napravlenii, protivopolozhnom napravleniyu dvizheniya Zemli po orbite (na samom dele, ona obrazuet s etim napravleniem ugol 5.15œ, no eto ne izmenyaet resheniya zadachi, tak kak dannyi ugol sushestvenno men'she ugla naklona zemnogo ekvatora k ekliptike).

 

 

Na vtorom risunke my vidim, chto podobnym obrazom ten' mozhet dvigat'sya po Zemle tol'ko astronomicheskoi osen'yu, to est' v promezhutke mezhdu osennim ravnodenstviem i zimnim solncestoyaniem.

Dannaya zadacha imeet real'nyi prototip - polnoe solnechnoe zatmenie 19 noyabrya 1816 goda, karta kotorogo privedena vyshe. Polosa polnoi fazy togda proshla cherez centr ili prigorody vseh semi gorodov, privedennyh v uslovii zadachi.

 

 

5. Uslovie. Znacheniya astronomicheskogo azimuta voshoda i posleduyushego zahoda nekotoroi planety v Sankt-Peterburge sostavili sootvetstvenno -90.0œ i +90.4œ. Zahod diska planety za gorizont dlilsya 3.2 sekundy. Chto eto za planeta, i mozhno li chto-to skazat' o vremeni goda, kogda eto proizoshlo?

 

5. Reshenie. Znacheniya azimutov tochek voshoda i zahoda ukazyvaet na to, chto planeta nahodilas' vblizi nebesnogo ekvatora. Tak kak planety raspolagayutsya na nebe vblizi ekliptiki, znachit, eto byla okrestnost' tochki vesennego ili osennego ravnodenstviya. Mezhdu voshodom i zahodom planety proshlo primerno 12 chasov. Azimut tochki zahoda po modulyu na 0.4œ prevoshodit azimut tochki voshoda, to est' za eti 12 chasov sklonenie planety uvelichilos'. Opredelim, naskol'ko ono uvelichilos'.

 

 

Iz risunka vidno, chto izmenenie modulya azimuta voshoda i zahoda DA svyazano s izmeneniem skloneniya ob'ekta Dd i shirotoi mesta nablyudeniya j (ravnoi +60œ) sootnosheniem:

 

Dd=DAcosj=+0.2œ.

 

Uchet atmosfernoi refrakcii ne izmenit etot rezul'tat, tak kak vblizi nebesnogo ekvatora refrakciya izmenyaet znacheniya azimutov voshoda i zahoda, no prakticheski ne izmenyaet ih raznost' DA. Dalee zametim, chto planeta dvizhetsya sredi zvezd vdol' ekliptiki - eto spravedlivo vsegda, krome momentov stoyanii planet, no togda ih uglovaya skorost' ochen' malen'kaya. Vblizi tochek ravnodenstviya ekliptika prohodit pod uglom e=23.4œ k nebesnym parallelyam (i ekvatoru), i polnoe uglovoe peremeshenie planety sredi zvezd za 12 chasov sostavit

 

 

V itoge, uglovaya skorost' planety sostavlyaet 1œ/sutki, chto prakticheski sovpadaet s uglovoi skorost'yu dvizheniya Solnca po nebu. Ni odna planeta ne mozhet dostich' takoi uglovoi skorosti vo vremya popyatnogo dvizheniya, da i pryamym dvizheniem s takoi skorost'yu mogut peremeshat'sya tol'ko dve vnutrennie planety, Merkurii i Venera, vo vremya epohi maksimal'nogo uglovogo rasstoyaniya ot Solnca.

Dlya togo chtoby opredelit', kakaya imenno eta planeta, opredelim ee vidimye razmery. Izvestno, chto prodolzhitel'nost' zahoda diska planety za gorizont Dt sostavila 3.2 sekundy. Nahodyas' vblizi nebesnogo ekvatora, planeta peremestilas' za eto vremya otnositel'no zemnogo nablyudatelya na uglovoe rasstoyanie l, ravnoe

 

l=15²Dt=48².

 

Uglovoi diametr planety sostavlyaet

 

d=2r=lcosj=24².

 

Poluchennoe znachenie sovpadaet s uglovymi razmerami diska Venery vo vremya ee naibol'shei elongacii (vidimyi razmer Merkuriya v eto vremya ne prevyshaet 8²). Planeta nahoditsya v naibol'shei elongacii, v 47œ ot Solnca i, dvigayas' v pryamom napravlenii, prohodit tochku vesennego ravnodenstviya. Esli eto naibol'shaya vostochnaya elongaciya, to kartina nablyudalas' v nachale fevralya, esli naibol'shaya zapadnaya elongaciya - v nachale maya.

 

 

6. Uslovie. Nahodyas' v tochke naibol'shei vostochnoi elongacii, Merkurii vstupil v soedinenie s Veneroi, bolee chem v 5 raz ustupaya ei po vidimomu diametru. U kakoi iz planet blizhaishee nizhnee soedinenie s Solncem proizoidet ran'she? Na skol'ko vremeni? Orbity Merkuriya, Venery i Zemli schitat' krugovymi.

 

6. Reshenie. Polozhenie Merkuriya, Venery i Zemli v ukazannyi v uslovii moment pokazano na risunke.

 

 

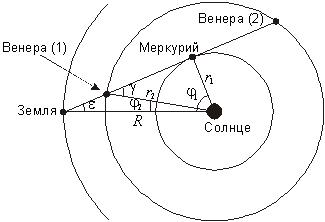
Nahodyas' v soedinenii s Merkuriem, Venera mozhet nahodit'sya v dvuh tochkah svoei orbity, pomechennyh na risunkah ciframi 1 i 2. No, kak uzhe bylo otmecheno v reshenii predydushei zadachi, uglovoi diametr Merkuriya v moment naibol'shei elongacii sostavlyaet okolo 8², sledovatel'no, uglovoi diametr Venery prevyshaet 40². Takoe mozhet byt', tol'ko esli Venera nahoditsya v polozhenii 1, nedaleko ot Zemli. Oboznachim radiusy orbit Merkuriya, Venery i Zemli cherez r₁, r₂ i R i opredelim raznost' geocentricheskih dolgot Zemli i kazhdoi iz dvuh vnutrennih planet j₁ i j₂ v dannyi moment. Dlya Merkuriya poluchaem

 

 

Raznica dolgot Zemli i Venery vychislyaetsya iz treugol'nika Solnce-Venera-Zemlya s uchetom svoistva smezhnyh uglov:

 

 

Vremya, ostavsheesya do nizhnego soedineniya vnutrennei planety, ravno

 

 

gde S - sinodicheskii period vnutrennei planety, ravnyi 115.9 sutkam dlya Merkuriya i 583.9 sutkam dlya Venery. Podstavlyaya chislennye znacheniya, poluchaem, chto nizhnee soedinenie Merkuriya proizoidet cherez 21.6 dnya, a nizhnee soedinenie Venery - cherez 15.6 dnei posle rassmatrivaemogo momenta. Takim obrazom, Venera vstupit v nizhnee soedinenie na 6 sutok ran'she Merkuriya.

 

 

7. Uslovie. Dva meteornyh roya dvizhutsya vokrug Solnca v tochnosti po odnoi i toi zhe orbite, no v raznyh napravleniyah. V odin moment vremeni oba roya vstrechayutsya drug s drugom i s Zemlei. Pri etom na Zemle nablyudayutsya dva meteornyh potoka s radiantami, imeyushimi koordinaty a=6ch, d=-66.6œ i a=18ch, d=0œ. Naiti ekscentrisitet orbity meteornyh roev. V kakuyu datu nablyudalis' meteornye potoki? Orbitu Zemli schitat' krugovoi.

 

7. Reshenie. Tak kak oba meteornyh roya dvizhutsya po odnoi i toi zhe orbite v raznye storony, v moment ih vstrechi oni budut imet' geliocentricheskie skorosti, ravnye po velichine i protivopolozhnye po napravleniyu. Radiant meteornogo potoka ukazyvaet napravlenie, protivopolozhnoe geocentricheskoi skorosti meteorov, poetomu radianty dvuh potokov ne okazalis' v protivopolozhnyh tochkah neba.

 

 

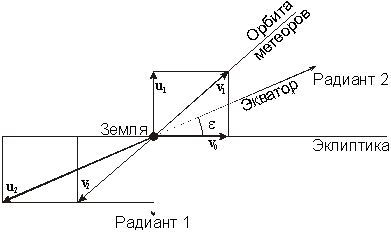
Oboznachim vektor skorosti Zemli cherez v₀, vektora geliocentricheskih skorostei meteornyh potokov cherez v₁ i v₂, a vektora ih geocentricheskih skorostei cherez u₁ i u₂. Dlya etih vektorov spravedlivy sootnosheniya

u₁ = v₁ - v₀,

u₂ = v₂ - v₀ = - v₁ - v₀.

 

Skladyvaya ih, poluchaem:

u₁ + u₂ = -2v₀.

 

Radiant pervogo meteornogo potoka nahoditsya v yuzhnom polyuse ekliptiki, sledovatel'no, ploskost' risunka, soderzhashaya vektor u₁, perpendikulyarna ploskosti ekliptiki, peresekaya ee po pryamoi, soderzhashei vektor v₀. Oba vektora perpendikulyarny radiusu-vektoru Zemli, napravlennomu iz centra Solnca, i vsya kartinnaya ploskost', v tom chisle i geliocentricheskie skorosti meteorov, perpendikulyarny linii Zemlya-Solnce. Sledovatel'no, v moment vstrechi s Zemlei meteory nahodilis' v tochke perigeliya ili afeliya svoei orbity, esli eta orbita ne krugovaya.

Tochka ekliptiki, v napravlenii kotoroi dvigalas' Zemlya v moment vstrechi s meteorami - odna iz dvuh tochek peresecheniya bol'shogo kruga ekliptiki i bol'shogo kruga kartinnoi ploskosti. Poslednii predstavlyaet soboi krug skloneniya, ohvatyvayushii vse tochki neba s pryamym voshozhdeniem 6ch i 18ch (v etom mozhno ubedit'sya po koordinatam radiantov potokov). Znachit, dve tochki peresecheniya bol'shih krugov - tochki solncestoyanii. Iz poslednego vektornogo uravneniya sleduet, chto proekcii vektorov u₂ i v₀ na ekliptiku imeyut protivopolozhnye znaki (tak kak vektor u₁ perpendikulyaren ekliptike). S uchetom koordinat vtorogo radianta delaem vyvod, chto dvizhenie Zemli napravleno v tochku solncestoyaniya, blizhaishuyu k radiantu vtorogo potoka - v tochku zimnego solncestoyaniya. Takoe napravlenie skorosti Zemlya imeet v den' vesennego ravnodenstviya - 21 marta. Ostaetsya otvetit' na pervyi vopros zadachi.

Ugol mezhdu napravleniem na vtoroi radiant (nebesnym ekvatorom) i skorost'yu dvizheniya Zemli e raven 23.4œ. Sproektirovav vektornoe vyrazhenie dlya summy skorostei u₁ i u₂ na dve koordinatnye osi, poluchaem:

 

u₁ = u₂ sine,

2v₀ = u₂ cose

 

i dalee

u₁ = 2v₀ tge.

 

Geliocentricheskaya skorost' meteorov v moment vstrechi s Zemlei ravna

 

 

Eta skorost' prevyshaet krugovuyu skorost' v₀, no ne prevoshodit vtoruyu kosmicheskuyu skorost'. Takim obrazom, orbita meteorov ellipticheskaya, i oni nahodyatsya v tochke perigeliya. Oboznachiv rasstoyanie ot Solnca do Zemli cherez r,š zapishem vyrazhenie dlya skorosti tela v perigelii:

 

 

Zdes' a - bol'shaya poluos' orbity meteornyh tel, e - ee ekscentrisitet, M - massa Solnca. V rezul'tate,

e=4tg²e=0.75.

 

 

8. Uslovie. S pomosh'yu Gigantskogo Opticheskogo Kosmicheskogo teleskopa so sverhvysokim uglovym razresheniem astronomy budushego smogli rassmotret' disk zvezdy Betel'geize (a Oriona). U kakogo ob'ekta poverhnostnaya yarkost' (yarkost' edinicy uglovoi ploshadi) bol'she - u Betel'geize ili u Venery? Vo skol'ko raz?

 

8. Reshenie. Dlya resheniya zadachi neobhodimo vspomnit', chto pri otsutstvii poglosheniya sveta poverhnostnaya yarkost' svetila ne zavisit ot ego rasstoyaniya do nablyudatelya. Obshaya yarkost' umen'shaetsya proporcional'no kvadratu rasstoyaniya, no v toi zhe proporcii umen'shaetsya i vidimaya ploshad' svetila. Dlya zvezd, samostoyatel'no izluchayushih energiyu, v priblizhenii absolyutno chernogo tela poverhnostnaya yarkost' opredelyaetsya tol'ko temperaturoi poverhnosti zvezdy, uvelichivayas' proporcional'no ee chetvertoi stepeni. Betel'geize - krasnyi sverhgigant spektral'nogo klassa M2 s temperaturoi poverhnosti okolo 3000 K, chto vdvoe men'she solnechnoi. Poverhnostnaya yarkost' Betel'geize budet v 16 raz men'she poverhnostnoi yarkosti Solnca.

Venera sama v vidimom diapazone spektra ne izluchaet, a tol'ko otrazhaet svet Solnca. Otnoshenie maksimal'noi poverhnostnoi yarkosti Venery (v centre diska vblizi verhnego soedineniya) i poverhnostnoi yarkosti Solnca budet ravno

 

 

Zdes' A - al'bedo Venery, r - radius Solnca i R - radius orbity Venery. V itoge, poverhnostnaya yarkost' Betel'geize v 2330 raz prevoshodit poverhnostnuyu yarkost' Venery.

 

 

9. Uslovie. Sharovoe zvezdnoe skoplenie imeet na nashem nebe blesk 4.5^m i vidimyi diametr 25¢. Rasstoyanie do skopleniya sostavlyaet 3 kpk. Schitaya, chto skoplenie sostoit iz zvezd, pohozhih na Solnce, ravnomerno raspredelennyh po ob'emu vnutri shara, ocenite osveshennost' na nochnoi storone obitaemoi planety, obrashayusheisya vokrug odnoi iz central'nyh zvezd skopleniya. Sravnite ee s osveshennost'yu v lunnuyu noch' na Zemle. Poglosheniem sveta v mezhzvezdnoi srede i v atmosfere planety prenebrech'.

 

9. Reshenie. Vyrazhaya uglovoi diametr skopleniya v radianah, umnozhaya na rasstoyanie do skopleniya i delya na 2, poluchaem radius skopleniya r₀, ravnyi 10.9 pk. Ob'em skopleniya raven

 

 

Solnce imeet absolyutnuyu zvezdnuyu velichinu M₀, ravnuyu +4.7^m. S rasstoyaniya d, ravnogo 3 kpk, ono vyglyadelo by kak zvezda velichiny m₀:

 

 

Oboznachiv zvezdnuyu velichinu vsego skopleniya cherez m, poluchaem vyrazhenie dlya kolichestva zvezd v skoplenii

 

 

i ob'emnoi koncentracii zvezd

 

 

Na nochnom nebe planety v centre skopleniya vidny zvezdy odnoi poloviny shara, ravnomerno zapolnyayushie ee po ob'emu. Oboznachim osveshennost', kotoruyu sozdaet na planete v centre skopleniya odna zvezda 0^m cherez J. Rasschitaem osveshennost', kotoruyu sozdadut na etoi planete vse zvezdy, popadayushie v tonkuyu polusfericheskuyu obolochku s radiusom r i tolshinoi Dr. Kolichestvo etih zvezd budet ravno proizvedeniyu koncentracii zvezd na ob'em obolochki:

 

 

Zvezdnaya velichina i osveshennost' ot kazhdoi zvezdy na planete sostavit

 

 

Zdes' r vyrazhaetsya v parsekah. Osveshennost' na nochnom nebe ot vseh zvezd polusfery ravna

 

 

My vidim, chto eta osveshennost' proporcional'na tolshine obolochki i ne zavisit ot ee radiusa. Predstavlyaya vsyu polusferu vnutri skopleniya kak slozhenie podobnyh obolochek, my poluchaem vyrazhenie dlya polnoi osveshennosti ot nochnogo neba planety:

 

 

Summarnaya zvezdnaya velichina vseh zvezd poloviny shara ravna

 

 

Nebo etoi planety budet znachitel'no yarche bezlunnogo nochnogo neba na Zemle, i svetila vne sharovogo skopleniya dadut lish' neznachitel'nyi vklad v ego yarkost'. No lunnaya noch' na Zemle (blesk polnoi Luny raven -12.7^m) vse zhe v 63 raza yarche, chem nebo planety v centre sharovogo skopleniya.

 

 

10. Uslovie. Galaktika imeet radius 15 kpk i znachitel'no men'shuyu tolshinu diska. Massa galaktiki ravna 10¹¹ mass Solnca i ravnomerno raspredelena po ob'emu galaktiki. Dve zvezdy obrashayutsya vokrug centra galaktiki v odnom napravlenii po krugovym orbitam s radiusami 5 i 10 kpk. Naiti sinodicheskii period pervoi zvezdy pri nablyudenii iz okrestnostei vtoroi zvezdy.

 

10. Reshenie. Massovaya plotnost' veshestva vnutri galaktiki r ravna

 

 

Zdes' M, R i d - massa, radius i tolshina diska galaktiki. V nekotorom priblizhenii mozhno schitat', chto pri vrashenii zvezdy po krugovoi orbite s radiusom r vnutri diska na nee budet vliyat' tol'ko ta chast' galaktiki, kotoraya zaklyuchena vnutri cilindra s radiusom r. Massa etoi chasti galaktiki ravna

 

 

Uglovaya skorost' vrasheniya zvezdy vokrug centra Galaktiki sostavit

 

 

Zdes' w₀ - uglovaya skorost' vrasheniya kraya galaktiki. Obratim vnimanie, chto zavisimost' uglovoi skorosti ot rasstoyaniya v dannom sluchae bolee slabaya, chem dlya keplerovskih orbit, gde my by poluchili stepen' -3/2. Sinodicheskii period zvezdy s radiusom orbity r₁ pri nablyudenii so zvezdy s radiusom orbity r₂ raven

 

 

Podstavlyaya chislennye znacheniya, poluchaem velichinu sinodicheskogo perioda: 1.07 milliardov let.

 

 

 

Versiya dlya pechati