Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 


Na pervuyu stranicu

Vverh: Vvedenie

Dalee: Deformiruemye zerkala

1. Poluchenie izobrazhenii pri turbulentnosti

1.1. Ideal'nyi teleskop

Airy function Forma izobrazheniya tochechnogo istochnika (zvezdy) v ideal'nom teleskope bez atmosfery opredelyaetsya tol'ko difrakciei i opisyvaetsya funkciei Eiri:


\begin{displaymath} P_0(\vec{\alpha}) = \frac{\pi D^2}{4 \lambda^2} \left[ \fra... .../\lambda)}{ \pi D \vert\vec{\alpha}\vert/\lambda)} \right] ^2, \end{displaymath} (1)

gde:

Pervoe temnoe kol'co nahoditsya na uglovom rasstoyanii $1.22 \lambda/D$ ot centra. Chasto eto rasstoyanie schitaetsya meroi razresheniya ideal'nogo teleskopa.

Izobrazhenie $I(\vec{\alpha})$ astronomicheskogo ob'ekta $O(\vec{\alpha})$ mozhno rassmatrivat' kak mnozhestvo izobrazhenii tochek, kazhdoe iz kotoryh opisyvaetsya funkciei Eiri. Eto mozhno zapisat' kak svertku:


\begin{displaymath} I(\vec{\alpha}) = \int {\rm d} \vec{\beta} \;\; O(\vec{\beta}) \;\; P_0(\vec{\alpha} - \vec{\beta}) = O \odot P_0. \end{displaymath} (2)

My nazyvaem eto uravneniem izobrazheniya. Po sravneniyu s ob'ektom izobrazhenie bolee sglazhennoe, razreshenie umen'shaetsya. Odnako, dlya zadannogo diametra teleskopa $D$ eto uhudshenie - naimen'shee vozmozhnoe. V etom sluchae my govorim, chto razreshenie v izobrazhenii ogranicheno difrakciei. Primer astronomicheskogo izobrazheniya (centr Galaktiki) s razlichnymi razresheniyami priveden nizhe.

Galactic Center

Vopros: Kak organichennoe difrakciei razreshenie zavisit ot dliny volny?

Vopros: Vychislite ogranichennoe difrakciei razreshenie chelovecheskogo glaza.

1.2. Funkciya rasseyaniya tochki

Chto proizoidet, esli teleskop ne idealen? Izobrazhenie tochechnogo istochnika ne budet tak horosho, kak funkciya Eiri, razreshenie uhudshitsya eshe sil'nee. No uravnenie izobrazheniya vse ravno ostanetsya v sile! Takim obrazom, funkciya rasseyaniya tochki (PSF) $P(\vec{\alpha})$ - eto vse, chto nuzhno dlya harakteristiki izobrazheniya. Shirina PSF - eto mera razresheniya.

Zamechanie 1. My neyavno prodpolagaem, chto v privedennyh vyshe uravneniyah $P(\vec{\alpha})$ opisyvaet izobrazhenie zvezdy edinichnoi intensivnosti, t.e. integral $P(\vec{\alpha})$ po $\alpha$ raven 1. Takim obrazom, uravnenie izobrazheniya sohranyaet polnyi potok ot astronomicheskogo ob'ekta, tol'ko po-raznomu raspredelyaet ego po pikselam.

Zamechanie 2. My predpolozhili, chto PSF imeet odinakovyi vid po vsemu polyu zreniya. Eto uslovie nazyvaetsya izoplanatizmom. Dlya astronomicheskih izobrazhenii eto ne vsegda spravedlivo, osobenno pri ispol'zovanii AO, tak kak PSF medlenno izmenyaetsya po polyu. V etom sluchae uravnenie izobrazheniya mozhno primenyat' k chastyam polya zreniya.


1.3. Kriterii razresheniya

Forma PSF mozhet byt' nepravil'noi; kak v etom sluchae kolichestvenno izmerit' razreshenie?

1. Polnaya shirina na urovne poloviny maksimuma (FWHM) PSF.

2. Chislo Shtrelya $ S = P(0)/P_0(0)$, to est' central'naya intensivnost' PSF po sravneniyu s central'noi intensivnost'yu funkcii Eiri. Chem vyshe chislo Shtrelya, tem luchshe razreshenie. Ogranichennoe difrakciei izobrazhenie - samoe luchshee, tak kak vsegda $S \leq 1$.

3. Energiya v kruge. Po opredeleniyu, integral PSF raven 1. Integral ot PSF v kruge radiusom $\beta$ nazyvaetsya energiei v kruge. Eta harakteristika vazhna pri nablyudeniyah slabyh ob'ektov, kogda neobhodimo kak mozhno luchshe skoncentrirovat' fotony.

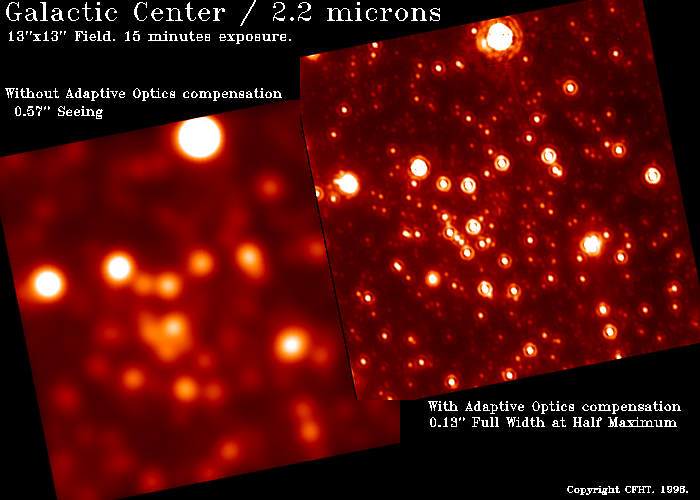
Primer PSF s ispravleniem turbulentnosti pokazan na risunke nizhe.

Vopros: Predpolozhim, chto PSF stala v dva raza uzhe, kak izmenitsya chislo Shtrelya?

Vopros: Kakim budet chislo Shtrelya, esli polovine ob'ektiva ideal'nogo teleskopa dat' fazovuyu zaderzhku v $\lambda/2$?


1.4. Opticheskaya peredatochnaya funkciya

Drugoi sposob opisaniya uravneniya izobrazheniya - eto ispol'zovanie preobrazovanii Fur'e (FT, budem oboznachat' ih til'doi). Svertka stanovitsya proizvedeniem, i


\begin{displaymath} \tilde{I}(\vec{f}) = \tilde{O}(\vec{f}) \cdot \tilde{P}(\vec{f}). \end{displaymath} (3)

Zdes' $\vec{f}$ eto prostranstvennaya chastota (esli $\alpha$ izmeryaetsya v radianah, to $f$ izmeryaetsya v obratnyh radianah).

$\tilde{P}(\vec{f})$ nazyvaetsya opticheskoi peredatochnoi funkciei (OTF). Ona opisyvaet izmenenie modulya i fazy FT ob'ekta v processe polucheniya izobrazhenii. Modul' OTF nazyvaetsya modulyacionnoi peredatochnoi funkciei (MTF). Dlya astronomicheskih (nekogerentnyh) izobrazhenii, $\vert\tilde{P}(\vec{f})\vert \leq 1$. Obychno MTF umen'shaetsya s uvelicheniem chastoty, poetomu melkie (vysokochastotnye) detali v izobrazhenii oslablyayutsya i v konechnom schete teryayutsya.

Izvestno, chto dlya lyuboi opticheskoi sistemy $\vert\tilde{P}(\vec{f})\vert =0$ dlya $\vert\vec{f}\vert \ge f_c$ , gde $f_c = D/\lambda$ nazyvaetsya chastotoi otsechki , $D$ - maksimal'nyi razmer apertury. Eto oznachaet, chto informaciya o prostranstvennyh chastotah vyshe $f_c$ bezvozvratno teryaetsya. Chtoby uvidet' malen'kie ob'ekty, nuzhny bol'shie teleskopy!

Sootnoshenie mezhdu PSF i OTF - eto preobrazovanie Fur'e, poetomu esli vy znaete odnu funkciyu, vy znaete i druguyu, eto razlichnye predstavleniya odnogo yavleniya. Iz svoistv preobrazovaniya Fur'e sleduet, chto $\tilde{P}(0) =1$ (normirovka PSF), i chto chislo Shtrelya proporcional'no integralu OTF po chastotam.

Vopros: Kakoi minimal'nyi razmer teleskopa potrebuetsya, chtoby razreshit' zabor s promezhutkami mezhdu plankami 10 sm s rasstoyaniya v 5 km?


1.5. Poluchenie izobrazhenii skvoz' atmosferu: dlinnye ekspozicii

OTF plots Atmosfernuyu turbulentnost' mozhno rassmatrivat' kak sluchainuyu fazovuyu aberraciyu, prilozhennuyu k teleskopu. Eti aberracii postoyanno izmenyayutsya so vremenem, i tak zhe vedet sebya PSF. Zdes' my rassmotrim srednyuyu PSF, sootvetstvuyushuyu dlinnym ekspoziciyam. Iz teorii sleduet vyrazhenie


\begin{displaymath} \tilde{P}_{\rm LE}(\vec{f}) = \tilde{P}_0(\vec{f}) \tilde{P}_a(\vec{f}). \end{displaymath} (4)

Gde $\tilde{P}_0(\vec{f})$ - OTF teleskopa (smotri vyshe) i $\tilde{P}_a(\vec{f})$ - atmosfernaya peredatochnaya funkciya. Dlya bol'shih teleskopov s horoshim kachestvom optiki razreshenie polnost'yu opredelyaetsya atmosferoi, poetomu my prenebregaem pervym chlenom i $ \tilde{P}_{\rm LE} \approx \tilde{P}_a$. Konechno, atmosfernaya PSF $P_{\rm LE}$ poluchena preobrazovaniem Fur'e iz $\tilde{P}_{\rm LE}$.

OTF atmosfery svyazana so statistikoi atmosfernyh fazovyh aberracii, tak nazyvaemoi fazovoi strukturnoi funkciei $D_{\phi}(\vec{r})$ (smotri sleduyushii razdel):


\begin{displaymath} \tilde{P}_a(\vec{f}) = \exp [-0.5 D_{\phi}(\lambda \vec{f}) ]. \end{displaymath} (5)

Zamechanie: V etoi formule my perehodim ot prostranstvennyh koordinat v ploskosti volnovogo fronta k prostranstvennym chastotam v ploskosti izobrazheniya, umnozhennym na dlinu volny. Eto sootnoshenie sleduet iz volnovoi optiki: kazhdaya Fur'e-komponenta izobrazheniya sozdaetsya interferenciei svetovyh voln, razdelennyh opredelennym rasstoyaniem. Etot princip ispol'zuetsya v radio- i opticheskih interferometrah.

Vopros: Predpolozhim, chto forma atmosfernoi PSF - gaussova. Kakova sootvetstvuyushaya forma strukturnoi funkcii?

Vopros: Zavisit li forma atmosfernoi PSF ot strukturnoi funkcii v oblasti, gde $D_{\phi} \ll 1$ and $D_{\phi} \gg 1$?


1.6. Statistika turbulentnosti

Iskazhennyi atmosferoi volnovoi front mozhno predstavit' kak smyatyi list bumagi. Volna, prihodyashaya ot zvezdy, pered vhozhdeniem v atmosferu ploskaya. Zatem nekotorye ee chasti prohodyat cherez vozduh teplee srednego (men'shii pokazatel' prelomleniya) i uhodyat vpered, drugie chasti otstayut, i ploskii volnovoi front deformiruetsya. Zadacha adaptivnoi optiki - skompensirovat' eti iskazheniya. No vnachale my dolzhny opisat' ih v statisticheskom smysle.

Vozduh obladaet nekotoroi dispersionnoi sposobnost'yu, no obychno etim prenebregayut, i vozmusheniya opticheskogo puti $l(\vec{x})$ rassmatrivayutsya kak ahromatichnye. Odnako, faza opticheskoi volny $\phi(\vec{x}) = \frac{2\pi}{\lambda}l(\vec{x})$ sil'no zavisit ot dliny volny $\lambda$! Govorya o vozmusheniyah, my predpolagaem, chto ih srednee znachenie ravno nulyu, $\langle \phi \rangle = 0$ (uglovye skobki oboznachayut statisticheskoe usrednenie).

Hotya sluchainye processy, podobnye $\phi(\vec{x})$ obychno opisyvayutsya korrelyacionnymi ili kovaricionnymi funkciyami, v issledovaniyah atmosfery predpochitayut strukturnye funkcii. Strukturnaya funkciya - eto srednyaya raznost' mezhdu dvumya znacheniyami sluchainogo processa:


Distorted wave-front
\begin{displaymath} D_{\phi}(\vec{r}) = \langle [ \phi(\vec{x}+\vec{r}) - \phi(\vec{x})]^2 \rangle. \end{displaymath} (6)

Vopros: Kakovo sootnoshenie mezhdu strukturnoi funkciei i funkciei kovariacii $B(\vec{r}) = \langle \phi(\vec{x}+\vec{r}) \phi(\vec{x}) \rangle$?

Vopros: Kak atmosfernaya $D_{\phi}(\vec{r})$ zavisit ot dliny volny $\lambda$?

Kolmogorovskaya model' turbulentnyh iskazhenii zadaet opredelennuyu formu fazovoi strukturnoi funkcii, a imenno


\begin{displaymath} D_{\phi}(\vec{r}) = 6.88 \left( \frac{\vert\vec{r}\vert}{r_0} \right) ^{5/3}. \end{displaymath} (7)

V etoi formule tol'ko odin parametr, $r_0$, kotoryi nazyvaetsya radiusom atmosfernoi kogerentnosti ili parametrom Frida. Uchityvaya, chto dlina puti ahromatichna, my poluchaem, chto $r_0 \propto \lambda^{6/5}$. Opredelyaya $r_0$, vsegda ukazyvaite sootvetstvuyushuyu dlinu volny!

Eta model', hotya ona i mozhet pokazat'sya primitivnoi, yavlyaetsya osnovaniem vsei teorii polucheniya izobrazhenii skvoz' turbulentnost', vklyuchaya adaptivnuyu optiku. Konechno, model' ploho rabotaet na bol'shih (bol'she neskol'kih metrov) i malyh (men'she 1 sm) rasstoyaniyah, no okazyvaetsya, chto eto ne ochen' vazhno.

Vorpos: Kakovo srednekvadratichnoe razlichie atmosfernoi fazy na dline bazy $r=r_0$ v radianah i v dlinah voln?

Vopros: Esli $r_0 =15$ sm na dline volny 0.5 mikron, to chemu ravno $r_0$ na dline volny 2.2 mikrona?

Teper' my podstavim etu model' v atmosfernuyu OTF dlya dlinnyh ekspozicii, i poluchim ee v forme:


\begin{displaymath} \tilde{P}_a(\vec{f}) = \exp [-3.44 (\lambda \vert\vec{f}\vert/r_0 )^{5/3} ]. \end{displaymath} (8)

Primeniv preobrazovanie Fur'e k etomu uravneniyu, poluchim atmosfernuyu funkciyu rasseyaniya tochki dlya dlinnyh ekspozicii. Chislennye raschety dayut sootnoshenie mezhdu FWHM atmosfernoi PSF (nazyvaemoi $\beta_{0.5}$, ili kachestvom izobrazheniya) i $r_0$:


\begin{displaymath} \beta_{0.5} = 0.98 \lambda / r_0. \end{displaymath} (9)

Na dline volny 0.5 mikron, kachestvo izobrazheniya v 1 sekundu sootvetstvuet $r_0$=10.1 cm.

Chislo Shtrelya atmosfernoi PSF tochno takoe zhe, kak dlya ideal'nogo teleskopa diametrom $r_0$ (eto prichina poyavleniya strannogo koefficienta 6.88) Takim obrazom, dlya bol'shogo teleskopa $D \ll r_0$, chislo Shtrelya ravno prosto $S=(r_0/D)^2$.

Vopros: Chemu ravno chislo Shtrelya dlya izobrazheniya s dlinnoi ekspoziciei dlya 4-m teleskopa pri kachestve izobrazheniya 1 sekunda na dlinah voln 0.5 i 2.2 mikrona?

Radius Frida $r_0$ inogda otozhdestvlyayut s harakternoi shkaloi atmosfernyh vozmushenii. Eto ne sovsem verno: my vidim, chto zakon Kolmogorova ne imeet kakoi-libo harakternoi shkaly. Odnako, tol'ko vozmusheniya s razmerom poryadka $r_0$ imeyut znachenie dlya izobrazhenii s dlinnymi ekspoziciyami. Na men'shih razmerah iskazheniya mnogo men'she, chem $\lambda$, na bol'shih razmerah $D_{\phi}$ stanovitsya takim bol'shim, chto atmosfernaya OTF ravna nulyu.

Lokal'naya velichina turbulentnyh fluktuacii indeksa prelomleniya v vozduhe opisyvaetsya strukturnoi postoyannoi indeksa prelomleniya $C_n^2$ kotoryi izmeryaetsya v strannyh edinicah, m$^{-2/3}$. Zavisimost' $C_n^2$ ot vysoty nazyvaetsya profilem turbulentnosti. Kachestvo izobrazheniya zavisit ot summarnogo vliyaniya vseh sloev atmosfery:


\begin{displaymath} r_0^{-5/3} = 0.423 \frac{2 \pi}{\lambda} \sec z \int_0^{H_max} C_n^2(h) {\rm d}h, \end{displaymath} (10)

gde $h$ - vysota, $z$ - zenitnyi ugol, i integrirovanie provoditsya ot teleskopa do maksimal'noi vysoty turbulentnosti (okolo 20 km).

Turbulence profile.

Na etom risunke pokazan primer profilya turbulentnosti v otnositel'nyh edinicah v Serro Paranal (sploshnaya liniya). Dolya turbulentnoi energii do dannoi vysoty pokazana shtrihovoi liniei. Hotya v etom primere znachitel'naya chast' turbulentnosti skoncentrirovana v dvuh sloyah, vse zhe okolo 1/3 obshei energii ravnomerno raspredeleno po vsem vysotam.

Vopros: Ispol'zuya eto sootnoshenie, naidite, kak $r_0$ i kachestvo izobrazheniya zavisyat ot zenitnogo ugla $z$.


1.7. Atmosfernaya postoyannaya vremeni

Atmospheric time constant Chasto turbulentnost' mozhno smodelirovat' kak ekrany, dayushie postoyannyi sdvig fazy, kotorye peremeshayutsya vetrom pered teleskopom. Znaya prostranstvennye svoistva fazovyh ekranov (strukturnuyu funkciyu) i skorost' vetra, mozhno ustanovit' vremennoe povedenie vozmushenii. Atmosfernaya postoyannaya vremeni $\tau_0$ opredelyaetsya kak


\begin{displaymath} \tau_0 = 0.31 \frac{r_0}{\bar{V}}, \end{displaymath} (11)

gde $\bar{V}$ - skorost' vetra, usrednennaya po vysote. Parametr $\tau_0$ opredelyaet, kakoi bystroi dolzhna byt' sistema adaptivnoi optiki.

Vopros: Vzyav tipichnoe znachenie $\bar{V}$=20 m/s, kakoi budet atmosfernaya postoyannaya vremeni na dlinah voln 0.5 i 2.2 mikrona pri kachestve izobrazheniya 1 sekunda?

Izobrazheniya astronomicheskih ob'ektov, poluchennye s ekspoziciyami $\tau_0$ ili koroche, nazyvayutsya izobrazheniyami s korotkimi ekspoziciyami. Oni sootvetstvuyut fiksirovannym (zamorozhennym) atmosfernym aberraciyam. Dlya bolee dlinnyh ekspozicii aberracii usrednyayutsya, i dlya ekspozicii, namnogo dlinnee $\tau_0$ mozhno poluchit' PSF dlya dlinnyh ekspozicii.


1.8. Izoplanaticheskii ugol

Isoplanatic angle Atmosfernaya PSF dlya dlinnyh ekspozicii ne zavisit ot napravleniya (izoplanatichna), tak kak turbulentnost' i ee strukturnaya funkciya statisticheski odinakovy v pole zreniya. Odnako momental'nye atmosfernye fazovye aberracii zavisyat ot napravleniya: dlya uglovogo rasstoyaniya 10 sekund smeshenie lucha zreniya teleskopa v atmosfernom sloe na vysote 10 km sostavit 0.5 m.

Standartnoe opredelenie atmosfernogo izoplanaticheskogo ugla $\theta_0$ - eto

\begin{displaymath} \theta_0 = 0.31 \frac{r_0}{\bar{h}}, \end{displaymath} (12)

gde $\bar{h}$ - eto nekotoraya harakternaya srednyaya vysota turbulentnosti. Beretsya srednee vzveshennoe $C_n^2(h)$ profilya s $h^{5/3}$, v rezul'tate dlya tipichnyh uslovii poluchaetsya dostatochno bol'shaya vysota $\bar{h} \approx 10$ km.

Vopros: Chemu raven izoplanaticheskii ugol $\theta_0$ dlya dlin voln 0.5 i 2.2 mikrona pri kachestve izobrazheniya 1 sekunda?

Eto yavlenie predstavlyaet ochen' bol'shuyu problemu dlya adaptivnoi optiki, tak kak ono ogranichivaet rasstoyanie mezhdu opornoi zvezdoi i issleduemym ob'ektom. Okazyvaetsya, chto dlya bol'shinstva ob'ektov net podhodyashih (yarkih i blizkih) opornyh zvezd, poetomu neobhodimy iskusstvennye lazernye opornye zvezdy. Kak al'ternativnyi metod, dlya uvelicheniya ispravlyaemogo polya zreniya mozhno popytat'sya primenit' trehmernoe ispravlenie turbulentnosti ( mul'ti-sopryazhennuyu adaptivnuyu optiku, MCAO).


1.9. Mody Zernike

V optike aberracii chasto predstavlyayut summoi special'nyh polinomov, nazyvaemyh polinomami Zernike. Sluchainye atmosfernye aberracii mozhno predstavit' v tom zhe vide; odnako, koefficienty etih aberracii (rasfokusirovki, astigmatizma i t.d.) budut sluchainymi funkciyami, izmenyayushimisya so vremenem.

Polinomy Zernike $Z_n^m(r,\theta)$ opredelyayutsya v polyarnyh koordinatah $(r,\theta)$ na okruzhnosti s edinichnym radiusom $(r<1)$. Oni harakterizuyutsya radial'nym poryadkom $n$ i azimutal'nym poryadkom $m$ (dlya dannogo $n$, $m$ prinimaet znacheniya ot 0 do $n$). Chasto vmesto dvuh indeksov $n$ i $m$ ispol'zuetsya posledovatel'naya numeraciya s odnim indeksom $j$. Dlya dannogo radial'nogo poryadka $N$ sushestvuet $(N+1)(N+2)/2$ polinomov Zernike.

Pervye mody Zernike nazvany tak zhe, kak izvestnye aberracii, i imeyut prostoi smysl (smotri tablicu pervyh 15 mod Zernike).


Preimushestva ispol'zovaniya mod Zernike vytekayut iz togo, chto oni yavlyayutsya ortonormal'nymi, to est' skalyarnoe proizvedenie $(Z_i, Z_j)$ ravno 1, esli $i=j$ i ravno nulyu v drugih sluchayah. Skalyarnoe proizvedenie opredelyaetsya kak integral po aperture teleskopa:


\begin{displaymath} (Z_i, Z_j) = \pi ^{-1} \int_{\vert\vec{r}\vert<1 } {\rm d} \vec{r} Z_i(\vec{r}) Z_j(\vec{r}). \end{displaymath} (13)

Teper' lyubaya fazovaya aberraciya $\phi (\vec{r})$ vnutri zrachka teleskopa mozhet byt' predstavlena kak beskonechnaya summa polinomov Zernike


\begin{displaymath} \phi(\vec{r}) = \sum_{j=1}^{\infty} a_j Z_j(\vec{r}), \end{displaymath} (14)

i koefficienty opredelyayutsya kak skalyarnye proizvedeniya:


\begin{displaymath} a_j = (\phi, z_j). \end{displaymath} (15)

Chasto ogranichennoe chislo mod Zernike uzhe daet dostatochno horoshee predstavlenie atmosfernyh aberracii. Esli eti mody ispravlyayutsya adaptivnoi optikoi, to poluchaetsya izobrazhenie s kachestvom, prakticheski neotlichimym ot opredelyaemogo difrakciei.

Moda porshen' sootvetstvuet postoyannoi faze, kotoraya ne vliyaet na izobrazhenie. Obychno eta moda ignoriruetsya.

Vopros: 4-m teleskop $f/15$, rasfokusirovan na 1 mm. Vychislite voznikayushuyu aberraciyu $a_4$ dlya dlin voln 0.5 i 2.2 mikrona.

Vopros: Predpolozhim, chto atmosfernaya aberraciya soderzhit tol'ko sluchainye naklony s odinakovymi amplitudami $\langle a_2 \rangle = \langle a_3 \rangle = A$. Zapishite sootvetstvuyushuyu fazovuyu strukturnuyu funkciyu.

Ortonormal'nost' mod Zernike predostavlyaet prostuyu vozmozhnost' vychislit' dispersiyu fazy, prointegrirovannuyu po zrachku. Dlya odnoi mody eto $a_j^2$. Dispersiya vseh mod ravna summe kvadratov koefficientov, nachinaya s vtorogo (porshen' isklyuchaetsya).


1.10. Statistika atmosfernyh koefficientov Zernike

V ramkah modeli turbulentnosti Kolmogorova my mozhem poluchit' statisticheskie svoistva koefficientov $a_j$, sootvetstvuyushih atmosfernym fazovym aberraciyam. Matematicheskie preobrazovaniya privodyat k prostoi formule:


\begin{displaymath} \langle a_i a_j \rangle = c_{ij} \left( \frac{D}{r_0} \right) ^{5/3}, \end{displaymath} (16)

gde koefficienty $c_{ij}$ - eto elementy tak nazyvaemoi matricy Nollya. Koefficienty nizkogo poryadka (do radial'nogo poryadka 3) privedeny nizhe.


i \ j 2 3 4 5 6 7 8 9 10
2 0.449 0 0 0 0 0 0.0142 0 0
3 0 0.449 0 0 0 0.0142 0 0 0
4 0 0 0.0232 0 0 0 0 0 0
5 0 0 0 0.0232 0 0 0 0 0
6 0 0 0 0 0.0232 0 0 0 0
7 0 0.0142 0 0 0 0.00619 0 0 0
8 0.0142 0 0 0 0 0 0.00619 0 0
9 0 0 0 0 0 0 0 0.00619 0
10 0 0 0 0 0 0 0 0 0.00619


Kak vy vidite, matrica Nollya pochti diagonal'naya (odnako dlya bolee vysokih poryadkov eto uzhe ne tak). Pochemu koefficient $c_{11}$ otsutstvuet? Dlya kolmogorovskoi turbulentnosti on beskonechen! Odnako pervaya moda (porshen') ne imeet znacheniya dlya izobrazhenii.

Vopros: Dlya 4-m teleskopa i kachestva izobrazheniya 1 sekunda, vychislite srednekvadratichnuyu amplitudu naklona v radianah (dlya dliny volny 0.5 mikron). Perevedite ee v srednekvadratichnuyu amplitudu dvizheniya izobrazheniya zvezdy. Zavisit li eta amplituda ot dliny volny?

Chto proizoidet, esli my ispravim pervye mody s pomosh'yu adaptivnoi optiki? Sootvetstvuyushie koefficienty obratyatsya v nuli, i polnaya dispersiya fazy umen'shitsya. Oboznachaya usrednennuyu po zrachku dispersiyu fazy kak $\langle \epsilon ^2 \rangle$, my zapishem


\begin{displaymath} \langle \epsilon ^2 \rangle = \left( \frac{D}{r_0} \right) ^... ...{\infty} c_{jj} = \left( \frac{D}{r_0} \right) ^{5/3} \Delta_J \end{displaymath} (17)

gde pervye $J$ mody Zernike ispravleny.

Polnaya neispravlennaya atmosfernaya fazovaya dispersiya (vse mody krome porshnya) sootvetstvuet $\Delta_1 = 1.0299$. Drugimi slovami, v teleskope s diametrom apertury $r_0$ atmosfernaya fazovaya dispersiya sostavlyaet primerno 1 kvadratnyi radian. Esli naklony ispravleny, to $\Delta_3 = 0.134$. Eto oznachaet, chto naklony sostavlyayut 87% polnoi dispersii fazy. Ispravlyaya mody do radial'nogo poryadka 2, poluchim $\Delta_6 = 0.0648$, radial'nyi poryadok 3 ostavlyaet neispravlennuyu dispersiyu $\Delta_{10} = 0.0401$. Kak vy vidite, dal'neishee umen'shenie dispersii fazy trebuet ispravleniya vse bol'shego chisla mod Zernike.

Dlya bol'shogo chislo ispravlennyh mod $J$ ($J>10$, chto proishodit v real'nyh sistemah), ochen' polezna asimptoticheskaya formula Nollya:


\begin{displaymath} \Delta_J \approx 0.2944 J^{-\sqrt{3}/2} \end{displaymath} (18)

Vopros: Ispol'zuya znacheniya $\Delta_J$ i $c_{ij}$ dannye vyshe, vychislite $\Delta_4$.

Skol'ko mod nuzhno ispravit'? Optiki znayut, chto kogda ostatochnaya faza men'she 1 radiana, kachestvo izobrazheniya priblizhaetsya k ogranichennomu difrakciei. Teper' u nas est' vse, chtoby opredelit' neobhodimoe chislo mod kak funkciyu diametra teleskopa, kachestva izobrazheniya i dliny volny! Dostatochno zapisat' $\langle \epsilon ^2 \rangle =1$ i podstavit' syuda vse formuly ( popytaites' sdelat' eto!). V rezul'tate poluchim


\begin{displaymath} J \approx 0.24 \left( \frac{D}{r_0} \right) ^{1.92}. \end{displaymath} (19)

Vopros: Skol'ko mod Zernike neobhodimo ispravit' na 4-m teleskope dlya izobrazhenii na dlinah voln 0.5 i 2.2 mikrona pri kachestve izobrazheniya 1 sekunda?

Neobhodimo li ispravlyat' turbulentnost', ispol'zuya mody Zernike? Razumeetsya, net, fazovye aberracii mogut byt' izmereny i ispravleny s pomosh'yu lyubogo drugogo nabora bazovyh funkcii, ili voobshe bez vsyakih mod, neposredstvenno vozdeistvuya na volnovoi front. Okazyvaetsya, chto mody Zernike - eto vtoroi po kachestvu nabor mod (luchshii nabor nazyvaetsya modami Karunena-Loeva). Vybor zavisit ot chisla kontroliruemyh parametrov (mod), neobhodimogo dlya dostizheniya trebuemoi stepeni ispravleniya; dlya mod Zernike ono men'she, chem dlya lokal'nogo kontrolya volnovogo fronta.

Vyvody. V etoi glave byli kratko izlozheny osnovy polucheniya izobrazheniya v ideal'nom teleskope i s prisutstviem aberracii (PSF, OTF, ogranichenie difrakciei, chislo Shtrelya). Zatem byli vvedeny osnovnye parametry atmosfery, imeyushie otnoshenie k adaptivnoi optike (fazovaya strukturnaya funkciya, kachestvo izobrazheniya, $r_0$, postoyannaya vremeni i izoplanaticheskii ugol). Issledovano razlozhenie sluchainyh fazovyh aberracii po modam Zernike. Teper' my mozhem opredelit' chislo mod, kotorye neobhodimo ispravit'.


VVERH: Vvedenie

DALEE: Deformiruemye zerkala

Publikacii s klyuchevymi slovami: adaptivnaya optika - atmosfera - volnovoi front
Publikacii so slovami: adaptivnaya optika - atmosfera - volnovoi front
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mnenie chitatelya [1]
Ocenka: 3.1 [golosov: 99]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya