Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu

VVERH: Vvedenie

DALEE: Lazernye opornye zvezdy

3. Datchiki volnovogo fronta

3.1. Trebovaniya k datchikam volnovogo fronta

Zadacha izmereniya iskazhenii volnovogo fronta chasto vstrechaetsya v optike (naprimer, pri izgotovlenii i ispytanii zerkal dlya teleskopov), i obychno reshaetsya s pomosh'yu interferometrov. Pochemu by ne ispol'zovat' standartnye lazernye interferometry v datchikah volnovogo fronta (WFS) dlya adaptivnoi optiki?

Vo-pervyh, sistema adaptivnoi optiki dolzhna ispol'zovat' svet zvezd, prohodyashii skvoz' turbulentnuyu atmosferu, chtoby izmeryat' volnovye fronty, i sledovatel'no, ispol'zovat' nekogerentnye (a chasto i netochechnye) istochniki. Dazhe lazernye opornye zvezdy nedostatochno kogerentny, chtoby rabotat' v obychnyh interferometrah. WFS dolzhny rabotat' s nekogerentnymi istochnikami belogo sveta.

Vo-vtoryh, interferencionnye uzory hromatichny. My ne mozhem pozvolit' propuskat' svet zvezd cherez fil'tr, tak kak my hotim ispol'zovat' slabye zvezdy. WFS dolzhny ochen' effektivno ispol'zovat' fotony.

V-tret'ih, interferometry opredelyayut fazu s neopredelennost'yu v $2\pi$, v to vremya kak atmosfernye iskazheniya fazy obychno prevoshodyat $2\pi$. WFS dolzhny obladat' lineinost'yu vo vsem diapazone atmosfernyh iskazhenii. Sushestvuyut algoritmy dlya "razvertyvaniya" fazy, pozvolyayushie ustranit' etu neopredelennost', no oni rabotayut medlenno, a atmosfernaya turbulentnost' izmenyaetsya bystro, s harakternym vremenem v millisekundy: WFS dolzhny byt' bystrymi.

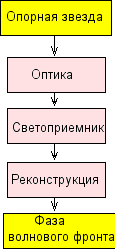
Etim trebovaniyam udovletvoryayut neskol'ko sushestvuyushih principov ustroistva WFS. Kazhdyi WFS sostoit iz sleduyushih osnovnyh komponentov:

Generic WFS

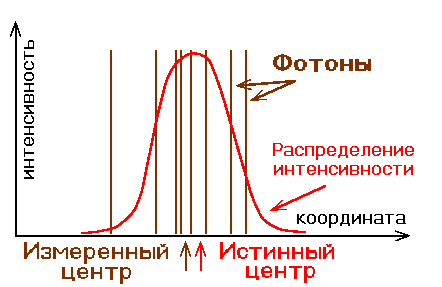
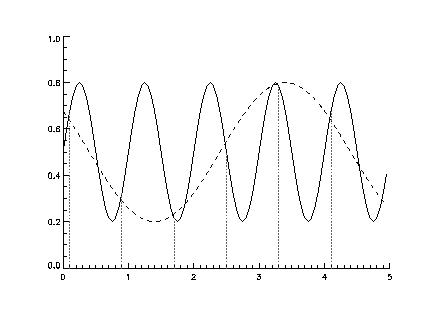Aliasing illustration Ne stoit govorit', chto lyuboi real'nyi WFS imeet konechnoe prostranstvennoe razreshenie, kotoroe dolzhno sootvetstvovat' razmeru korrektiruyushih elementov (to est' rasstoyaniyu mezhdu aktuatorami v deformiruemom zerkale). Iskazheniya volnovogo fronta s men'shimi razmerami ne dolzhny vosprinimat'sya. Odnako, oni vliyayut na signal WFS, vyzyvaya tak nazyvaemuyu oshibku sovmesheniya (podobno oshibke sovmesheniya vo vremennyh signalah s konechnoi diskretizaciei, smotri risunok). Spektr turbulentnosti umen'shaetsya k vysokim prostranstvennym chastotam, poetomu oshibka sovmesheniya chasto mala po sravneniyu s drugimi oshibkami adaptivnoi optiki, v chastnosti s oshibkoi approksimacii.

3.2. Datchiki volnovogo fronta Sheka-Gartmana

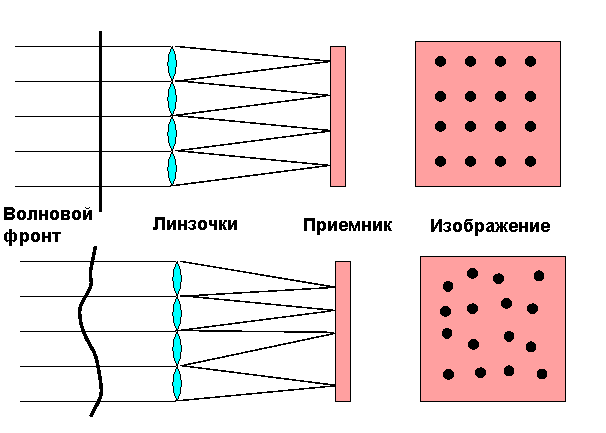
Shack-Hartmann WFS

Horosho izvestnyi test Gartmana, pervonachal'no razrabotannyi dlya ispytaniya optiki teleskopov, byl primenen v adaptivnoi optike v naibolee rasprostranennom tipe WFS. Izobrazhenie vyhodnogo zrachka proektiruetsya na massiv linz - dvumernuyu reshetku iz malen'kih odinakovyh linz. Kazhdaya linza zanimaet maluyu chast' apertury, nazyvaemuyu subzrachkom, i stroit izobrazhenie istochnika. Vse izobrazheniya stroyatsya na odnom detektore, obychno na PZS.

Kogda vhodyashii volnovoi front ploskii, vse izobrazheniya raspolozheny v pravil'nom poryadke, opredelyaemom geometriei massiva linz. Kogda volnovoi front iskazhaetsya, izobrazheniya smeshayutsya ot svoih zadannyh polozhenii. Smeshenie centroida izobrazheniya v dvuh perpendikulyarnyh napravleniyah $x,y$ proporcional'ny srednim naklonam volnovogo fronta po $x,y$ v subaperturah. Takim obrazom, WFS Sheka-Gartmana (S-H WFS) izmeryaet naklony volnovogo fronta. Sam volnovoi front vosstanavlivaetsya po massivu izmerennyh naklonov, s tochnost'yu do postoyannoi, kotoraya ne igraet roli pri postroenii izobrazheniya. Razreshenie S-H WFS ravno razmeru subapertury.

Vopros: Kakov maksimal'nyi uglovoi razmer istochnika, pri kotorom nachnut perekryvat'sya izobrazheniya ot sosednih subapertur? Voz'mite razmer linzy 0.5 mm i fokal'noe rasstoyanie 50 mm. Podhodit li takoi massiv linz dlya sistemy adaptivnoi optiki s razmerom subapertury $d$=1 m?

Vopros: Ocenite srednekvadratichnye naklony volnovyh frontov na subaperturah kak funkciyu razmera subapertury $d$ i $r_0$ (ispol'zuite koefficienty atmosfernyh naklonov iz razdela 1.10). Vychislite dlya $d$=1 m i kachestva izobrazheniya 1 sekunda.

Preimushestvo S-H WFS v tom, chto on polnost'yu ahromatichen, naklony ne zavisyat ot dliny volny. On takzhe mozhet rabotat' s netochechnymi (protyazhennymi) istochnikami. Esli $\phi(\vec{r})$ - eto faza volnovogo fronta, to naklon po x, izmeryaemyi S-H WFS, vychislyaetsya kak


\begin{displaymath} x = \frac{\lambda}{ 2 pi S} \int_{sub-aperture} \frac{\partial \phi(\vec{r})}{\partial r_x} \; {\rm d}\vec{r}, \end{displaymath} (1)

gde $S$ - ploshad' subapertury. Naklony po x,y ocenivayutsya po smesheniyu centroidov izobrazhenii (centrov tyazhesti), kak


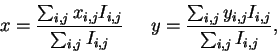\begin{displaymath} x = \frac{\sum_{i,j} x_{i,j}I_{i,j}}{\sum_{i,j} I_{i,j}} \;\... ...;\; y = \frac{\sum_{i,j} y_{i,j}I_{i,j}}{\sum_{i,j} I_{i,j}}, \end{displaymath} (2)

gde $I_{i,j}$ - eto intensivnosti sveta na pikselah detektora. Predpolagaetsya, chto koordinaty x,y vyrazheny v radianah (eto mozhno sdelat', znaya masshtab izobrazheniya na detektore).

Photon noise of centroid Teper' mozhno ocenit' oshibku opredeleniya naklona iz-za fotonnogo shuma. Pust' $\beta$ radianov - eto radius izobrazheniya, formiruemogo kazhdoi subaperturoi. Dlya protyazhennyh istochnikov $\beta$ ravno razmeru istochnika (tochnee, dispersii raspredeleniya intensivnosti vokrug centra). Dlya tochechnyh istochnikov $\beta=\lambda/d$ esli subapertury men'she, chem $r_0$ (izobrazheniya, ogranichennye difrakciei), ili $\beta = \lambda/r_0$ dlya bol'shih subapertur (razmer izobrazheniya opredelyaetsya atmosfernym drozhaniem). Raspredelenie intensivnosti v izobrazhenii mozhno rassmatrivat' kak raspredelenie plotnosti veroyatnosti prihodyashih fotonov. Sledovatel'no, kazhdyi prihodyashii foton pozvolyaet opredelit' polozhenie izobrazheniya s oshibkoi $\beta$. Esli $n$ fotonov zaregistrirovany za vremya ekspozicii, fotonnaya oshibka polozheniya centroida (t.e. naklona) budet ravna $\beta/\sqrt{n}$, kak posle povtoreniya izmereniya $n$ raz.

V fotometricheskom diapazone R (dlina volny okolo 600 nm), gde chuvstvitel'nost' sovremennyh detektorov maksimal'na, zvezda 0 velichiny daet potok v 8000 fotonov v sekundu na kvadratnyi santimetr na nanometr polosy propuskaniya (effektivnaya polosa propuskaniya mozhet dlya horoshego PZS dostigat' 300 nm). Dlya zvezdy velichiny m potok umen'shitsya v $10^{-0.4m}$ raz. Pri vychislenii potoka, dostupnogo detektoru WFS, neobhodimo prinyat' vo vnimanie opticheskoe propuskanie.

Vopros: Vychislite kolichestvo fotonov, zaregistrirovannyh za ekspoziciyu v 1 ms v subaperture 1 m ot zvezdy 15-i velichiny. Prinyat' polnoe propuskanie 0.3 i kvantovuyu effektivnost' 0.6.

Obsheprinyato vyrazhat' vse oshibki volnovogo fronta v radianah. My umnozhim oshibku naklona na $\frac{2\pi}{\lambda} d$, chtoby poluchit' dispersiyu razlichiya fazy mezhdu krayami subapertury v kvadratnyh radianah:


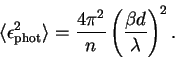\begin{displaymath} \langle \epsilon_{\rm phot}^2 \rangle = \frac{4 \pi^2}{n} \left( \frac{ \beta d}{\lambda} \right) ^2. \end{displaymath} (3)

Bud'te ostorozhny pri ispol'zovanii etoi formuly: zdes' $\lambda$ - dlina volny, na kotoroi sistema adaptivnoi optiki stroit izobrazhenie, v to vremya kak razmer izobrazheniya $\beta$ neobhodimo vychislit' dlya dliny volny, na kotoroi rabotaet datchik volnovogo fronta, a ona mozhet byt' drugoi.

Vopros: Skol'ko fotonov neobhodimo nakopit', chtoby dobit'sya fotonnoi oshibki v 1 radian v S-H WFS s $d = 3 r_0$? Prinyat', chto poluchenie izobrazheniya i issledovanie volnovogo fronta osushestvlyayutsya na odnoi dline volny.

Oshibka vosstanovleniya volnovyh frontov proporcional'na $\langle \epsilon_{\rm phot}^2 \rangle$ s koefficientom, nazyvaemym rasprostranenie shuma. Izvestno, chto dlya S-H WFS rasprostranenie shuma poryadka edinicy i lish' nemnogo uvelichivaetsya s kolichestvom elementov (naklony integriruyutsya rekonstruktorom, poetomu shum ne usilivaetsya).

Fotonnyi shum proporcionalen kvadratu razmera subapertury $d$. Eto oznachaet, chto dlya dannogo $\beta$, fotonnaya oshibka S-H WFS ne zavisit ot razmera ego subapertury. Etot vyvod veren tol'ko dlya ideal'nogo detektora; v real'nyh sistemah s PZS (naprimer, NAOS na VLT) dlya bolee slabyh opornyh zvezd ispol'zuyutsya bol'shie subapertury.

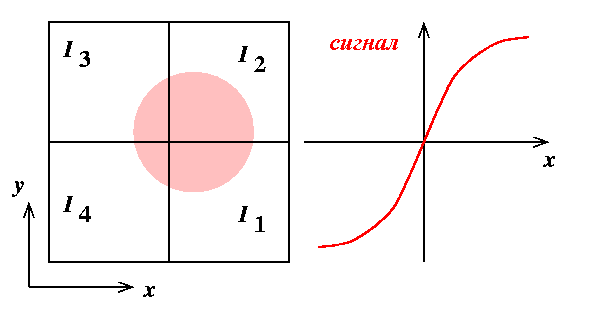Quad-cell Skol'ko pikselov v detektore dolzhno byt' otvedeno na kazhduyu subaperturu? Chtoby tochno vychislit' polozhenie centroidov, kazhdoe individual'noe izobrazhenie dolzhno stroit'sya dostatochno detal'no, i na kazhduyu subaperturu neobhodimo bolee 4h4 pikselov. Odnako kazhdyi piksel PZS priemnika daet shum schityvaniya, kotoryi dlya slabyh opornyh zvezd dominiruet v fotonnom shume. Poetomu v nekotoryh konstrukciyah (naprimer, Altair dlya Dzhemini-Sever) na kazhduyu subaperturu prihoditsya tol'ko 2h2 piksela. V etom sluchae kazhdyi element rabotaet kak kvadratnaya yacheika, i naklony po x,y vychislyayutsya iz otnoshenii intensivnosti:


\begin{displaymath} x \approx \frac{\beta}{2} \; \frac{I_1 +I_2 - I_3 - I_4}{I_1... ...beta}{2} \; \frac{I_2 +I_3 - I_1 - I_4}{I_1 +I_2 + I_3 + I_4}. \end{displaymath} (4)

Reakciya detektora naklona s kvadratnoi yacheikoi lineina tol'ko dlya naklonov men'shih, chem $\pm \beta/2$, koefficient reakcii proporcionalen $\beta$ (i poetomu mozhet izmenyat'sya, v zavisimosti ot kachestva izobrazheniya ili razmera ob'ekta). Eto cena, kotoruyu nuzhno zaplatit' za uvelichenie chuvstvitel'nosti, kotoraya imeet pervostepennoe znachenie dlya astronomov.

Vopros: Kakoi dolzhna byt' forma izobrazheniya opornoi zvezdy, chtoby dobit'sya v tochnosti lineinoi krivoi reakcii kvadratnoi yacheiki?

S-H WFS shiroko rasprostraneny, tak kak oni osnovany na proverennoi tehnologii i bogatom opyte, kompaktny i stabil'ny. Eti WFS trebuyut kalibrovki nominal'nogo polozheniya pyatna, kotoraya proizvoditsya pri poluchenii izobrazheniya iskusstvennogo tochechnogo istochnika.

3.3. Datchiki iskrivleniya

Metod izmereniya iskrivleniya volnovogo fronta razrabatyvalsya F.Roddierom s 1988 g. Ego ideya sostoyala v neposredstvennom soedinenii bimorfnogo zerkala s datchikom iskrivleniya (CS), pri kotorom otpadet neobhodimost' v promezhutochnyh vychisleniyah (hotya eto tak i ne bylo osushestvleno).

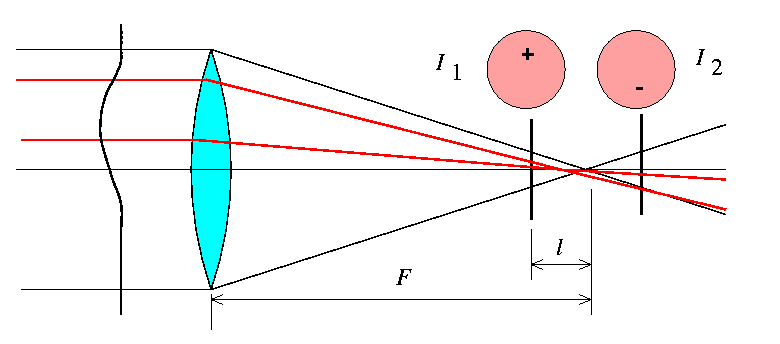
Curvature sensing

Pust' $I_1(\vec{r})$ - raspredelenie intensivnosti sveta v predfokal'nom izobrazhenii zvezdy, rasfokusirovannom na nekotoroe rasstoyanie $l$, a $I_2(\vec{r})$ - sootvetstvuyushee raspredelenie intensivnosti v zafokal'nom izobrazhenii. Zdes' $\vec{r}$ - koordinata v ploskosti izobrazheniya i $F$ - fokusnoe rasstoyanie teleskopa. Dva etih izobrazheniya - kak by izobrazheniya zrachka, umen'shennye s faktorom $\frac{l}{F-l}$. V priblizhenii geometricheskoi optiki mestnye iskrivleniya volnovogo fronta delayut odno izobrazhenie yarche, a drugoe slabee; normalizovannuyu raznicu intensivnostei mozhno zapisat' kak


\begin{displaymath} \frac{I_1(\vec{r}) -I_2(\vec{r})}{I_1(\vec{r}) +I_2(\vec{r})... ...triangledown^2 \phi \left( \frac{F \vec{r}}{l}\right) \right]. \end{displaymath} (5)

Operator $\bigtriangledown^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$ nazyvaetsya laplasianom i ispol'zuetsya dlya vychisleniya krivizny raspredeleniya fazy $\phi(\vec{x})$. Pervyi chlen v etom uravnenii - eto gradient fazy na krayu apertury (simvolicheski eto zapisyvaetsya kak chastnaya proizvodnaya po napravleniyu, perpendikulyarnomu krayu, umnozhennaya na "kraevuyu funkciyu" $\delta_c$). CS ahromatichen (vspomnite, chto $\phi(\vec{x})$ obratno proporcional'no $\lambda$). Hotya formula vyglyadit slozhnoi, ee smysl yasen. Vazhnym yavlyaetsya to, chto chuvstvitel'nost' CS obratno proporcional'na rasfokusirovke $l$.

Vopros: Narisuite pary pred- i zafokal'nyh izobrazhenii dlya aberracii Zernike ot 2 do 6.

Dlya istochnika s konechnym uglovym razmerom $\beta$ pred- i zafokal'nye izobrazheniya razmyty na velichinu $\beta(F-l)$. Razmytie dolzhno byt' men'she proekcii razmera subapertury $d$:


\begin{displaymath} \beta (F-l) < \frac{l}{F}d \end{displaymath} (6)

Rasfokusirovka vsegda namnogo men'she fokusnogo rasstoyaniya $F$, sledovatel'no, uslovie minimal'noi rasfokusirovki imeet vid:


\begin{displaymath} l > \beta \frac{f^2}{d}. \end{displaymath} (7)

Dlya izmereniya volnovogo fronta s bol'shim razresheniem trebuetsya bol'shaya rasfokusirovka, sootvetstvenno umen'shaetsya chuvstvitel'nost' CS. Eto oznachaet, chto CS mozhet ispytyvat' trudnosti s izmereniem aberracii vysokogo poryadka.

Dlya tochechnyh istochnikov i bol'shih subapertur (sluchai, predstavlyayushii prakticheskii interes) razmytie $\beta$ opredelyaetsya atmosfernymi aberraciyami, $\beta = \lambda/r_0$, kak i dlya S-H WFS. Esli sistema adaptivnoi optiki rabotaet po zamknutomu ciklu i ostatochnye aberracii (na dline volny raboty WFS) stanovyatsya maly, razmytie umen'shaetsya do $\beta=\lambda/d$, pozvolyaya umen'shit' rasfokusirovku i uvelichit' chuvstvitel'nost'. Eto svoistvo do nekotoryh predelov deistvitel'no ispol'zuetsya v real'nyh sistemah adaptivnoi optiki: rasfokusirovka umen'shaetsya, kogda cikl zamykaetsya.

Iskazheniya volnovogo fronta s vysokoi chastotoi (men'she, chem razmer subapertury) imeyut spektr moshnosti (dispersiyu amplitud Fur'e), proporcional'nyi $f^{11/6}$, no ih spektr krivizny proporcionalen $f^{1/6}$ i mozhet vyzvat' bol'shuyu oshibku sovmesheniya. Chtoby ne dopustit' etogo, signal dolzhen byt' sglazhen pered razdeleniem na subapertury. Sglazhivanie osushestvlyaetsya umen'sheniem rasfokusirovki $l$, kotoraya takzhe uvelichivaet chuvstvitel'nost'. V obshem, vybor $l$ ves'ma kritichen dlya CS, ego neobhodimo podstraivat' pri izmenenii kachestva izobrazheniya. Signal CS - eto tol'ko bolee ili menee gruboe priblizhenie deistvitel'noi krivizny volnovogo fronta...

My privedem bez vyvoda formulu dlya dispersii fazy iz-za fotonnogo shuma v CS, kogda rasfokusirovka podstroena do optimal'nogo znacheniya:

\begin{displaymath} \langle \epsilon_{\rm phot}^2 \rangle = \frac{\pi^2}{n} \left( \frac{\beta d}{\lambda} \right) ^2 . \end{displaymath} (8)

Kak i dlya S-H WFS, eto dispersiya dlya odnoi subapertury. My vidim, chto vyrazheniya dlya S-H i CS ochen' pohozhi. Chtoby poluchit' polnuyu oshibku volnovogo fronta, $\langle \epsilon_{\rm phot}^2 \rangle$ nuzhno umnozhit' na koefficient rasprostraneniya shuma, kotoryi dlya CS proporcionalen kolichestvu subapertur $N$ (on proporcionalen logarifmu $N$ dlya S-H). Pri rekonstrukcii volnovogo fronta nizkie chastoty usilivayutsya, poetomu shum v osnovnom smeshaetsya k modam s nizkim poryadkom. Eto ukazyvaet na potencial'nuyu problemu pri ispol'zovanii CS v sistemah adaptivnoi optiki vysokogo poryadka. Podrobnoe komp'yuternoe modelirovanie sistemy AO Dzhemini (~200 aktuatorov) pokazalo, chto effektivnost' datchikov S-H i CS pochti odinakova (Applied Optics, V. 36, P. 2856, 1997).

Gradient sensing Masshtab pred- i zafokal'nyh izobrazhenii zavisit ot rasfokusirovki $l$ kotoruyu neobhodimo izmenyat' vo vremya raboty. Eto neudobno; v deistvitel'nosti signal krivizny registriruetsya v izobrazhenii zrachka s fiksirovannym masshtabom, v to vremya kak velichina rasfokusirovki podstraivaetsya s pomosh'yu special'nogo opticheskogo ustroistva (smotri nizhe). Vneshnie subapertury proektiruyutsya na granicu zrachka, ih signal daet informaciyu o radial'nyh gradientah fazy, vklyuchaya obshie naklony (smotri risunok).

Datchiki iskrivleniya v deistvuyushih sistemyh adaptivnoi optiki (naprimer, v PUEO i Hokupa'a ) ispol'zuyut v kachestve svetopriemnikov lavinnye fotodiody (APD). Eto, kak i fotoumnozhiteli - odnokanal'nye ustroistva. Individual'nye fotony detektiruyutsya i prevrashayutsya v elektricheskie impul'sy bez shuma schityvaniya i s malym temnovym tokom, maksimal'naya kvantovaya effektivnost' okolo 60%. Individual'nye segmenty zrachka vydelyayutsya reshetkoi iz linz (kotoraya obychno sootvetstvuet radial'noi geometrii bimorfnogo deformiruemogo zerkala), zatem svet ot kazhdogo segmenta fokusiruetsya i peredaetsya na sootvetstvuyushii fotodiod po steklovoloknu. Kolichestvo fotodiodov ravno chislu segmentov. Vneshnie segmenty otslezhivayut kraya apertury, i ih signaly proporcional'ny gradientam volnovogo fronta vdol' normali.

Optical scheme of CS

Lavinnye fotodiody - bol'shie i dorogie, poetomu eta konstrukciya prigodna tol'ko dlya sistem nizkogo poryadka. Dlya togo, chtoby na kazhdyi piksel prihodilsya odin detektor, pred- i zafokal'nye izobrazheniya poperemenno podayutsya na odin fotodiod, zatem signal demoduliruetsya v komp'yutere volnovogo fronta. Modulyaciya fokusnogo rasstoyaniya osushestvlyaetsya s pomosh'yu koleblyushegosya membrannogo zerkala, pomeshennogo v fokal'noi ploskosti (tipichnaya chastota 2 KGc). Rasfokusirovka $l$ obratno proporcional'na amplitude kolebanii membrany, kotoraya podstraivaetsya k izmenyayushemusya kachestvu izobrazhenii i mozhet byt' umen'shena, kogda cikl upravleniya adaptivnoi optikoi zamykaetsya, uvelichivaya chuvstvitel'nost' detektora iskrivleniya. Poleznaya kompensaciya turbulentnosti byla dostignuta dazhe s takim nizkim signalom, kak 1 foton na subaperturu za odin cikl upravleniya!

Al'ternativnym resheniem mozhet byt' ispol'zovanie PZS kak svetopriemnikov v CS. Eto obsuzhdaetsya uzhe dolgoe vremya, odnako v deistvuyushih sistemah poka ne osushestvleno. Nedostatok PZS - shum schityvaniya, kotoryi pri nizkom urovne svetovyh potokov stanovitsya dominiruyushim shumom. V Evropeiskoi Yuzhnoi observatorii byli razrabotany special'nye PZS, kotorye pozvolyayut osushestvit' neskol'ko ciklov modulyacii za odno schityvanie.

Vopros: Predpolozhim, chto PZS s shumom schityvaniya 5 elektronov ispol'zuetsya v WFS. Kakim dolzhno byt' chislo zaregistrirovannyh fotonov $n$, chtoby shum schityvaniya stal men'she fotonnogo shuma?

3.4. Drugie datchiki volnovogo fronta

Shearing interferometer Trudnosti interferometricheskih izmerenii volnovogo fronta mozhno preodolet', esli interferiruyushie luchi predstavlyayut soboi volnovye fronty s nebol'shim bokovym sdvigom $\vec{\rho}$ (eto nazyvaetsya interferometrom sdviga). Esli sdvig men'she $r_0$, razlichie fazy men'she odnoi dliny volny, i otsutstvuet neopredelennost' v $2\pi$. Intensivnost' sveta v interferogramme budet ravna


\begin{displaymath} I(\vec{r}) = \vert e^{i \phi(\vec{r})} + e^{i \phi(\vec{r}+\... ...t[ \rho \frac{\partial \phi(\vec{r})}{\partial \rho} \right]. \end{displaymath} (9)

Dlya malyh sdvigov razlichie fazy proporcional'no pervoi proizvodnoi (naklonu), sledovatel'no, signal interferometra sdviga pohozh na signal S-H WFS. Dva sdviga v perpendikulyarnyh napravleniyah neobhodimy, chtoby izmerit' naklony x,y. V pervoi udachnoi sisteme adaptivnoi optiki (RTAC) ispol'zovalsya datchik volnovogo fronta, osnovannyi na interferometre sdviga, no teper' etot metod polnost'yu ostavlen v pol'zu S-H WFS.

Vopros: Ocenite maksimal'nyi sdvig $\vec{\rho}$, chtoby sohranit' lineinuyu reakciyu interferometra sdviga pri dannom kachestve izobrazheniya (zadano $r_0$).

Drugie tipy interferometrov byli predlozheny dlya ispol'zovaniya v detektorah volnovogo fronta. Nekotorye mogut davat' signaly, pryamo proporcional'nye faze (takim obrazom otpadaet neobhodimost' v rekonstruktore), hotya i v ogranichennom dinamicheskom diapazone. Nekotorye resheniya mogut predstavlyat' interes dlya ispravleniya ostatochnyh aberracii vysokogo poryadka (t.e. v sistemah adaptivnoi optiki s ochen' vysokoi stepen'yu kompensacii, neobhodimyh dlya obnaruzheniya ekstrasolnechnyh planet).

Pyramid WFS

Piramidal'nyi datchik volnovogo fronta (P-WFS) razrabatyvaetsya ital'yanskimi astronomami. Prozrachnaya piramida pomeshena v fokal'noi ploskosti i rassekaet izobrazhenie zvezdy na chetyre chasti. Kazhdyi puchok prelomlyaetsya, i luchi formiruyut chetyre izobrazheniya zrachka teleskopa na odnoi PZS-matrice. Takim obrazom, kazhdaya subapertura registriruetsya chetyr'mya pikselami PZS. Opticheskaya shema pohozha na ispytanie s pomosh'yu nozha Fuko.

Predpolozhim, chto istochnik sveta protyazhennyi, i budem ispol'zovat' geometricheskuyu optiku. Naklon volnovogo fronta v kakoi-libo subaperture izmenyaet polozhenie istochnika na piramide, sledovatel'no izmenyaetsya svetovoi potok, registriruemyi chetyr'mya pikselami, kotoryi v drugom sluchae byl by odinakovym. Vychislyaya normalizovannye raznosti intensivnostei, my poluchim dva signala, proporcional'nye naklonam volnovogo fronta v dvuh napravleniyah. Chuvstvitel'nost' P-WFS zavisit ot razmera istochnika $\beta$. P-WFS mozhno rassmatrivat' kak massiv kvadratnyh yacheek, on pohozh na S-H WFS.

Chto proishodit, kogda ispol'zuetsya tochechnyi istochnik (zvezda) i prinimaetsya vo vnimanie vliyanie difrakcii? Raspredelenie intensivnosti v chetyreh izobrazheniyah zrachka stanovitsya slozhnoi nelineinoi funkciei formy volnovogo fronta, P-WFS bol'she ne izmeryaet naklony. V sluchae slabyh aberracii (amplituda mnogo men'she $\lambda$) formu volnovogo fronta vse zhe mozhno vosstanovit', hotya i bolee slozhnym sposobom. Dlya togo, chtoby vosstanovit' lineinost', zvezda bystro dvizhetsya nad vershinoi piramidy (naprimer, po krugu), sozdavaya kol'ceobraznyi istochnik. Eto ne modulyaciya (kak v CS), a prosto razmazyvanie tochechnogo istochnika, tak kak signal integriruetsya po odnomu ili neskol'kim ciklam drozhaniya.

Vopros: Narisuite izobrazheniya chetyreh zrachkov v P-WFS dlya sluchaya rasfokusirovki (moda Zernike nomer 6).

Kakovy preimushestva P-WFS? Vo-pervyh,otsutstvuet reshetka iz linz, subapertury opredelyayutsya pikselami detektora. Eto oznachaet, chto dlya slabyh zvezd chislo subapertur mozhno umen'shit' prosto binirovaniem PZS. Vo-vtoryh, amplitudu drozhaniya zvezdy mozhno podstraivat' dlya nailuchshego kompromissa mezhdu chuvstvitel'nost'yu (men'shee drozhanie) i lineinost'yu (bol'shee drozhanie). Dlya malyh amplitud chuvstvitel'nost' P-WFS mozhet byt' vyshe, chem S-H WFS (sm. Astron. Astrophys. V. 369, P. L9, 2001). Nakonec, vozmozhno (po krainei mere v principe) pomestit' neskol'ko piramid v fokal'noi ploskosti, chtoby ob'edinit' svet neskol'kih slabyh opornyh zvezd na odnom detektore. Nesmotrya na interes k P-WFS, poka net rabotayushih sistem adaptivnoi optiki s WFS takogo tipa.

Faza mozhet byt' opredelena iz analiza dvuh odnovremennyh izobrazhenii zvezdy, odno v fokuse i drugoe rasfokusirovannoe (ili, v obshem, s kakoi-libo izvestnoi aberraciei). Etot podhod nazyvaetsya fazovoe razlichie. Algoritm nelineinyi (i poetomu medlennyi?), preimushestva ego primeneniya v adaptivnoi optike poka ne yasny.

"Ideal'nyi" datchik volnovogo fronta eshe ne izobreten. Ne sushestvuet obshei teoremy, kotoraya by ustanovila absolyutnyi predel chuvstvitel'nosti lyubogo WFS iz-za fotonnogo shuma. Vmesto etogo, u nas est' neskol'ko empiricheskih reshenii, vozmozhnost' optimizirovat' ih parametry i vybirat' luchshie sredi imeyushihsya variantov.

3.5. Vosstanovlenie volnovogo fronta

V etom razdele problema vychisleniya formy volnovogo fronta na osnovanii dannyh WFS rassmatrivaetsya v obshem vide.

Izmereniya (dannye WFS) mozhno predstavit' kak vektor $S$ ( ego dlina ravna udvoennomu chislu subapertur N dlya S-H WFS, tak kak izmeryayutsya naklony v dvuh napravleniyah, i ravna N dlya CS). Neizvestnye (volnovoi front) - eto vektor $\phi$, kotoryi mozhet opredelen kak znacheniya fazy na koordinatnoi setke ili, chashe, kak koefficienty Zernike. Predpolagaetsya, chto sootnoshenie mezhdu izmereniyami i neizvestnymi lineinoe, po krainei mere v pervom priblizhenii. Samaya obshaya forma lineinogo sootnosheniya zadaetsya proizvedeniem matric,


\begin{displaymath} S = A \phi , \end{displaymath} (10)

gde matrica $A$ nazyvaetsya matricei vzaimodeistviya. V real'nyh sistemah adaptivnoi optiki matrica vzaimodeistviya opredelyaetsya eksperimental'no: vse vozmozhnye signaly (t.e. mody Zernike ) podayutsya na deformiruemoe zerkalo, i zapisyvaetsya reakciya datchika volnovogo fronta na eti signaly.

Matrica rekonstruktora B osushestvlyaet obratnuyu operaciyu, opredelyaya vektor volnovogo fronta iz izmerenii:

\begin{displaymath} \phi = B S. \end{displaymath} (11)

Vopros: Dlya dannogo kolichestva subapertur N, ocenite chislo arifmeticheskih operacii, neobhodimyh dlya vosstanovleniya fazy. Kak ono zavisit ot dliny volny, na kotoroi poluchaetsya izobrazhenie (dlya dannogo chisla Shtrelya)?

Kolichestvo izmerenii obychno bol'she chisla neizvestnyh, poetomu primenimo reshenie metodom naimen'shih kvadratov. V priblizhenii naimen'shih kvadratov my ishem takoi fazovyi vektor $\phi$, kotoryi nailuchshim obrazom opisyvaet dannye. Poluchennyi v rezul'tate rekonstruktor -


\begin{displaymath} B = ( A^T A)^{-1} A^T . \end{displaymath} (12)

Zdes' verhnii indeks T oznachaet transponirovannuyu matricu, a -1 - obratnuyu matricu. Deistviya s matricami ochen' chasto vstrechayutsya v zadachah adaptivnoi optiki.

Pochti vo vseh sluchayah obrashenie matricy vyzyvaet zatrudneniya, tak kak matrica $A^T A$ - singulyarnaya. Eto oznachaet, chto na nekotorye parametry (ili kombinacii parametrov) dannye ne nakladyvayut ogranichenii. Naprimer, my ne mozhem opredelit' pervuyu modu Zernike (porshen') iz izmerenii naklona. Na praktike obrashenie matricy osushestvlyaetsya s udaleniem neopredelennyh (ili ploho opredelnnyh) parametrov s pomosh'yu algoritma razlozheniya vyrozhdennyh znachenii. V sistemah Sheka-Gartmana s kvadratnoi geometriei, ploho opredelyaemye mody obychno vklyuchayut kvaziperiodicheskie deformacii s chastotoi reshetki aktuatorov.

Skol'ko mod Zernike mozhno vosstanovit' s pomosh'yu S-H WFS, imeyushego $N$ subapertur? Na pervyi vzglyad, do 2$N$. Na samom dele, tol'ko $N$, potomu chto naklony x,y ne polnost'yu nezavisimy, oni izbytochny. Dlya CS maksimal'noe chislo mod takzhe ravno $N$.

Rekonstruktor, ispol'zuyushii metod naimen'shih kvadratov, ne yavlyaetsya luchshim. Iz rukovodstv po statistike izvestno, chto luchshee vosstanovlenie mozhet byt' dostignuto s ispol'zovaniem apriornoi informacii o svoistvah signala. V sluchae adaptivnoi optiki takoi informaciei yavlyaetsya statistika vozmushenii volnovogo fronta (naprimer, kovariaciya mod Zernike) i statistika shuma WFS. Starayas' naiti reshenie, kotoroe daet minimal'nuyu ozhidaemuyu ostatochnuyu fazovuyu dispersiyu (sledovatel'no, maksimal'noe chislo Shtrelya), my poluchim matricu rekonstruktora, kotoraya pohozha na fil'tr Vinera.

V sluchae odnomernyh signalov fil'tr Vinera v prostranstve chastot zapisyvaetsya kak

\begin{displaymath} W(f) = \frac{ \tilde{A}^* \vert\tilde{S}\vert^2 } { \vert\tilde{A}\vert^2 \vert\tilde{S}\vert^2 + \vert\tilde{N}\vert^2}, \end{displaymath} (13)

gde $\vert\tilde{S}\vert^2$ and $\vert\tilde{N}\vert^2$ oboznachayut sootvetstvenno spektr moshnosti signala i shuma. Esli shumom mozhno prenebrech', to fil'tr Vinera svoditsya k obratnomu fil'tru $\tilde{A}^{-1}$, no on obrezaet chastoty, na kotoryh shum dominiruet nad signalom. Dlya adaptivnoi optiki eto oznachaet, chto i poryadok kompensacii, i shirina polosy servoustroistva umen'shayutsya pri nedostatochnom kolichestve fotonov.

Vopros: Prostranstvennyi spektr moshnosti oshibok naklona belyi (ne zavisit ot chastoty f) i spektr moshnosti atmosfernyh naklonov proporcionalen $f^{-8/3}$. Kak maksimal'naya chastota skompensirovannyh aberracii zavisit ot urovnya shuma $\vert\tilde{N}\vert^2$?

V sistemah adaptivnoi optiki vyrazheniya dlya minimal'noi dispersii rekonstruktora vklyuchayut matricu vzaimodeistviya i matricy kovariacii shuma i atmosfernyh vozmushenii. Shodnye rezul'taty poluchayutsya s ispol'zovaniem drugih statisticheskih podhodov (maksimum pravdopodobiya ili maksimal'naya posteriornaya veroyatnost').

Dlya lyubogo rekonstruktora B, shum vosstanovlennoi fazy $\langle \epsilon^2 \rangle$ raven


\begin{displaymath} \langle \epsilon^2 \rangle = \frac{1}{N} \;\; {\rm trace} (B C_S B^T), \end{displaymath} (14)

gde $C_S$ - matrica kovariacii izmerenii (diagonal'naya matrica s elementami $\langle \epsilon_{\rm phot}^2 \rangle$ v sluchae nekorrelirovannogo shuma), "trace" oznachaet summu diagonal'nyh elementov matric. Eto vyrazhenie pozvolyaet vychislit' koefficient rasprostraneniya shuma, svyazav oshibki izmerenii WFS s oshibkami vosstanovleniya faz.

Vyvody. Datchik volnovogo fronta - eto klyuchevaya chast' astronomicheskih sistem adaptivnoi optiki, tak kak opornye zvezdy chasto slabye, chto ogranichivaet dostizhimuyu stepen' ispravleniya turbulentnosti. Rassmotreny dva nibolee rasprostranennyh principa ustroistva datchikov volovogo fronta - Sheka-Gartmana i iskrivleniya. Dlya obeih my mozhem vychislit' fotonnuyu oshibku i ocenit' oshibki vosstanovleniya volnovogo fronta kak funkciyu velichiny opronoi zvezdy i parametrov sistemy. Osnovnye principy rekonstrukcii volnovogo fronta byli vvedeny bez uglubleniya v podrobnosti.

VVERH: Vvedenie

DALEE: Lazernye opornye zvezdy

Publikacii s klyuchevymi slovami: adaptivnaya optika - atmosfera - volnovoi front
Publikacii so slovami: adaptivnaya optika - atmosfera - volnovoi front
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mnenie chitatelya [1]
Ocenka: 3.1 [golosov: 99]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya