<< 1. Vvedenie | Oglavlenie | 3. Metody teorii special'nyh ... >>

2. Trudnosti integrirovaniya klassicheskih uravnenii

Uravneniya orbital'nogo dvizheniya v sisteme koordinat, svyazannoi s massivnym central'nym telom, mozhno predstavit' v vide

gde  - vektor polozheniya issleduemogo tela;  - vremya;  - gravitacionnyi parametr;  - keplerovskii chlen;  - vozmushayushie sily, prichem .

Integrirovanie etih uravnenii svyazano so sleduyushimi trudnostyami.

1. Pravye chasti uravnenii (1) predstavlyayut soboi bol'shie i bystroizmenyayushiesya funkcii dazhe dlya krugovyh orbit. Kak izvestno, vychislyaemye na komp'yutere bol'shie velichiny soderzhat bol'shie oshibki okrugleniya. Poetomu poshagovoe chislennoe integrirovanie klassicheskih uravnenii budet sopryazheno s bystrym nakopleniem oshibok okrugleniya.
2. Uravneniya (1) imeyut osobennost' v nachale koordinat ( 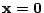). Dlya sil'no ekscentrichnyh ellipticheskih orbit v pericentre, pri sblizhenii s central'nym telom, velichiny pravyh chastei uravnenii znachitel'no i bystro vozrastayut. Poetomu integrirovanie orbity vblizi pericentra vypolnyaetsya s malym shagom i bol'shimi oshibkami.
3. Uravneniya (1) neustoichivy po Lyapunovu. Horosho izvestno, chto lyapunovskaya neustoichivost' differencial'nyh uravnenii pri chislennom integrirovanii sozdaet blagopriyatnye
   usloviya dlya usileniya vsevozmozhnyh oshibok, neizbezhno soprovozhdayushih lyuboi chislennyi process. Oshibki na tekushem shage integrirovaniya stanovyatsya oshibkami nachal'nyh dannyh sleduyushego, kotorye v dal'neishem usilivayutsya neustoichivost'yu shag za shagom.

Predlagaemye v rabote metody teorii special'nyh vozmushenii polnost'yu reshayut kazhduyu iz perechislennyh problem. Izlozhim obshie idei etih metodov.

---

<< 1. Vvedenie | Oglavlenie | 3. Metody teorii special'nyh ... >>

Publikacii s klyuchevymi slovami: Nebesnaya mehanika Publikacii so slovami: Nebesnaya mehanika

Sm. takzhe: Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Naum Il'ich Idel'son - 125 let so dnya rozhdeniya Zadacha N tel i problema integriruemosti K 90-letiyu Aleksandra Aleksandrovicha Orlova Dinamika zvezdnyh skoplenii Prosteishaya forma predstavleniya gradienta gravitacionnogo potenciala nebesnyh tel Evolyuciya elementov orbit Yupitera i Saturna na dlitel'nyh intervalah vremeni Vse publikacii na tu zhe temu >>