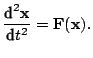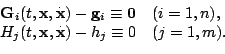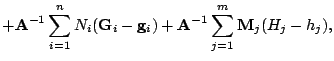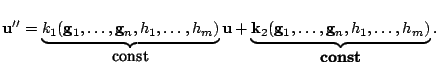<< 3. Metody teorii special'nyh ... | Oglavlenie | 3.2. Sglazhivayushie preobrazovaniya >>

3.1. Linearizaciya i regulyarizaciya

Cel' metodov linearizacii i regulyarizacii sostoit v tom, chtoby predstavit' uravneniya dvizheniya v lineinom i, samoe glavnoe, v regulyarnom vide.

Rassmotrim snachala uravneniya nevozmushennogo dvizheniya

Predpolozhim, chto uravneniya (2) imeyut integraly

Uslovie nezavisimosti integralov (3) ne obyazatel'no. Zdes' i  - vektornye i skalyarnye integral'nye funkcii sootvetstvenno, a i  - integral'nye parametry, kotorye v nevozmushennom dvizhenii postoyanny.

Dalee vvedem vremennoe i koordinatnoe preobrazovaniya:

kotorye pozvolyayut pereiti k novym peremennym i .

Glavnaya ideya linearizacii i regulyarizacii sostoit vo vvedenii v uravneniya, zapisannye v novyh peremennyh, integral'nyh sootnoshenii (3). V rezul'tate uravneniya prinimayut vid [1]

gde shtrih oznachaet proizvodnuyu po , a i  - neopredelennye koefficienty, kotorye zadayutsya takim obrazom, chtoby uravneniya prinimali lineinyi i regulyarnyi vid [1]

V vozmushennom sluchae, primenyaya vysheizlozhennye preobrazovaniya, budem imet' slabonelineinye uravneniya vida

Poskol'ku zdes' integral'nye parametry uzhe ne yavlyayutsya postoyannymi i, krome togo, vsledstvie poyavleniya pravaya chast' stanovitsya funkciei vremeni, sistemu (7) neobhodimo dopolnit' uravneniyami

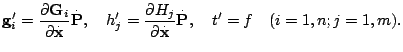
Takim obrazom, v rezul'tate podbora preobrazovanii (4), a takzhe koefficientov i mozhno poluchit' mnogochislennoe semeistvo sistem differencial'nyh uravnenii vida (7). Sredi takih sistem shiroko ispol'zuyutsya na praktike sistemy uravnenii v peremennyh Shperlinga-Bode [2] i Kustaanheimo-Shtifelya [3]. V pervoi

a v kachestve integralov vystupayut integraly energii i Laplasa; vo vtoroi

gde  - tak nazyvaemaya matrica Kustaanheimo-Shtifelya, a privedenie uravnenii k vidu (7) okazyvaetsya vozmozhnym pri ispol'zovanii lish' integrala energii.

---

<< 3. Metody teorii special'nyh ... | Oglavlenie | 3.2. Sglazhivayushie preobrazovaniya >>

Publikacii s klyuchevymi slovami: Nebesnaya mehanika Publikacii so slovami: Nebesnaya mehanika

Sm. takzhe: Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Naum Il'ich Idel'son - 125 let so dnya rozhdeniya Zadacha N tel i problema integriruemosti K 90-letiyu Aleksandra Aleksandrovicha Orlova Dinamika zvezdnyh skoplenii Prosteishaya forma predstavleniya gradienta gravitacionnogo potenciala nebesnyh tel Evolyuciya elementov orbit Yupitera i Saturna na dlitel'nyh intervalah vremeni Vse publikacii na tu zhe temu >>