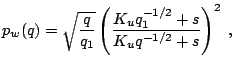<< 2.2. Effekt N 1: | Oglavlenie | 2.4. Effekt N 3: otrazhenie >>
2.3. Effekt N 2: rasprostranenie v neodnorodnoi srede
Teper' dopustim, chto oblako neodnorodno, no szhatiya net(
), poetomu pri nalichii AV vnov' vypolnyaetsya
priblizhenie (6). Pust' operator
, a
takzhe
, chto tipichno dlya AV. Togda iz
(5) sleduet, chto stacionarnoe (
) raspredelenie 
dostigaetsya pri
uslovii
otkuda nahodim
Sootnosheniya (10) vpervye vyvedeny eshe v 1944 g. soratnikom Al'vena doktorom Ualenom [9] opyat' zhe dlya razvitiya teorii solnechnyh pyaten. Vazhno, chto eti sootnosheniya universal'ny: oni ne zavisyat ot geometrii magnitnogo polya.
Iz svoistva
sleduet, chto u AV, begushih
snaruzhi vnutr' oblaka (v storonu uvelicheniya plotnosti), amplituda
vozmushenii skorosti padaet dazhe v otsutstvie poglosheniya. Etim
effektom mozhno ob'yasnit' [12] umen'shenie shiriny
spektral'nyh linii k centru nekotoryh PZO.
Otmetim, chto pri vypolnenii priblizheniya (6) vtoroi
chlen sprava v (5) mozhno preobrazovat' k vidu
, gde uchteno, chto
.
Togda vmesto (9) mozhno zapisat' uravnenie
kotoroe ves'ma chasto ispol'zuetsya v teorii voln (naprimer, [10]). Domashnee zadanie: s pomosh'yu uravneniya (11) dokazhite, chto pri perehode zvukovoi volny iz vozduha v stenku amplituda vozmushenii skorosti umen'shaetsya v sotni raz.
Iz sootnosheniya
sleduet, chto davlenie
AV,
, pomogaet teplovomu davleniyu borot'sya protiv
samogravitacii oblaka, nezavisimo ot napravleniya rasprostraneniya
volny. T. e. dazhe volny, vhodyashie v oblako snaruzhi, starayutsya ego
rasshirit'! Konechno, ne nado zabyvat', chto etot rezul'tat poluchen v
otsutstvie poglosheniya voln i pri uslovii, chto raspredelenie
amplitudy ne zavisit ot vremeni. Esli zhe pogloshenie vhodyashei volny
veliko, libo volna tol'ko nachinaet pronikat' v oblako, to ona
sdavlivaet oblako i sposobstvuet kollapsu.
Sravnivaya (8) i (10), my vidim, chto v
pokoyasheisya neodnorodnoi srede zavisimost' 
gorazdo
slabee, chem v odnorodno szhimayusheisya srede. Eto razlichie
ob'yasnyaetsya tem, chto pri szhatii chast' energii
krupnomasshtabnogo techeniya (porozhdennogo, naprimer,
samogravitaciei) perehodit v energiyu voln. Intuiciya podskazyvaet,
chto esli sreda i neodnorodna, i szhimaetsya, to zavisimost'
dolzhna lezhat' mezhdu
i
.
Okazyvaetsya, eto predpolozhenie mozhno proverit' analiticheski, esli predpolozhit', chto szhatie/rasshirenie yavlyaetsya stacionarnym. Ispol'zuya VKB priblizhenie, Parker [13] nashel raspredelenie amplitudy AV v stacionarnom sfericheski simmetrichnom zvezdnom vetre. Neskol'ko pozzhe Belcher [14] pokazal, chto rezul'tat Parkera mozhet byt' predstavlen kak funkciya plotnosti, kotoruyu my perepishem v vide
gde
- bezrazmernaya plotnost'; 
-
tochka, v kotoroi izvestny vse harakteristiki techeniya; 
-
otnoshenie skorosti techeniya k al'venovskoi skorosti v etoi tochke;
- znachenie 
v tochke, gde 
. Indeks 
, esli
volna idet v napravlenii magnitnogo polya 
, i 
dlya
vstrechnoi volny. Parametr mozhet byt' kak polozhitel'nym, tak
i otricatel'nym, poskol'ku uchityvaet napravlenie skorosti techeniya.
Zametim, chto v sluchae ochen' medlennogo szhatiya (
)
sootnoshenie (12) daet
. V
protivopolozhnom sluchae poluchaem
.
Povedenie 
v sluchayah, kogda skorost' techeniya otricatel'na i
po poryadku velichiny blizka k al'venovskoi skorosti (
), pokazano na ris. 2.
 |
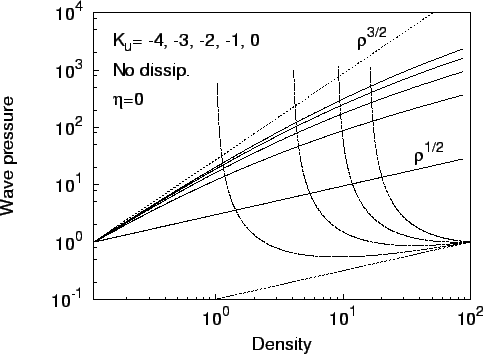Ris. 2.
Zavisimost' volnovogo davleniya |
v stacionarno szhimayushemsya sfericheskom oblake pri
razlichnyh skorostyah szhatiya (parametr 
) k centru (
) po techeniyu; shtrihovye
linii - dlya voln, idushih ot centra k krayu protiv techeniya.
Chem bol'she 
, tem vyshe profil'
Vidno, chto funkcii sushestvenno zavisyat ot napravleniya
rasprostraneniya volny (znaka 
). Esli volna napravlena protiv
techeniya, no al'venovskaya skorost' men'she skorosti techeniya, to
volna budet snosit'sya techeniem nazad. V tochke, gde eti skorosti
sravnivayutsya, u volny, idushei protiv techeniya, dolzhno proishodit'
beskonechnoe nakoplenie energii, odnako pri uchete dissipativnyh
effektov my poluchim, chto volna v etoi tochke polnost'yu pogloshaetsya
(pod'em shtrihovyh krivyh na ris. 2 smenitsya padeniem
k nulyu).
Podvodya itog, mozhno skazat', chto konkurenciya effektov N 1 i N 2 opredelyaetsya napravleniem rasprostraneniya volny i otnosheniem al'venovskoi skorosti k skorosti szhatiya.
<< 2.2. Effekt N 1: | Oglavlenie | 2.4. Effekt N 3: otrazhenie >>
|
Publikacii s klyuchevymi slovami:
MGD - al'venovskie volny - Plazma
Publikacii so slovami: MGD - al'venovskie volny - Plazma | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
