<< 3. Volny Rossbi v diske | Oglavlenie | 5. Effekty Rossbi na Solnce >>
4. Volny Rossbi v massivnyh
protozvezdnyh oblakah
1![]() . Nablyudeniya pokazyvayut, chto v ryade massivnyh
protozvezdnyh oblakov formiruyutsya odnovremenno neskol'ko molodyh
zvezdnyh ob'ektov. Pri etom zakonomernost'yu yavlyaetsya to, chto
kollimirovannye sverhzvukovye struinye vybrosy iz etih ob'ektov
orientirovany pod ochen' malym uglom drug k drugu v kazhdom oblake.
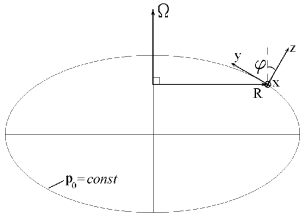
Na nash vzglyad, eto odnoznachno ukazyvaet na to, chto za ih
formirovanie otvetstven edinyi universal'nyi volnovoi mehanizm,
privodyashii k obrazovaniyu regulyarnyh struktur v oblake.
. Nablyudeniya pokazyvayut, chto v ryade massivnyh
protozvezdnyh oblakov formiruyutsya odnovremenno neskol'ko molodyh
zvezdnyh ob'ektov. Pri etom zakonomernost'yu yavlyaetsya to, chto
kollimirovannye sverhzvukovye struinye vybrosy iz etih ob'ektov
orientirovany pod ochen' malym uglom drug k drugu v kazhdom oblake.
Na nash vzglyad, eto odnoznachno ukazyvaet na to, chto za ih
formirovanie otvetstven edinyi universal'nyi volnovoi mehanizm,
privodyashii k obrazovaniyu regulyarnyh struktur v oblake.
Dlya proyasneniya prichin formirovaniya pochti parallel'nyh
struinyh vybrosov iz molodyh zvezdnyh ob'ektov, nahodyashihsya v
odnom protozvezdnom oblake, neobhodimo prezhde vsego opredelit'
prichinu vozniknoveniya u nih kvaziparallel'nyh momentov vrasheniya,
poskol'ku molodye zvezdy predstavlyayut soboi akkrecionno-struinye
sistemy, v kotoryh dzhety rasprostranyayutsya vsegda vdol' osi
vrasheniya okolozvezdnogo diska [1-3]. Takoi prichinoi mozhet byt'
effekt, obuslovlennyi deistviem sily Koriolisa - volny Rossbi
[4], a vposledstvii - formirovanie dolgozhivushih vihrei Rossbi,
horosho issledovannyh v geofizike i fizike planetnyh atmosfer (sm.
[5-7], tam zhe ssylki na original'nye raboty).
Rassmatrivaemaya nami situaciya znachitel'no otlichaetsya ot obsuzhdaemyh v [5-7] principial'noi neobhodimost'yu ucheta samogravitacii, poskol'ku harakternaya dlina volny Dzhinsa v lyubom sluchae mnogo men'she harakternogo masshtaba oblaka, inache ne proishodili by ego gravitacionnyi kollaps i uzh tem bolee obrazovanie neskol'kih molodyh zvezd v etom oblake.
|
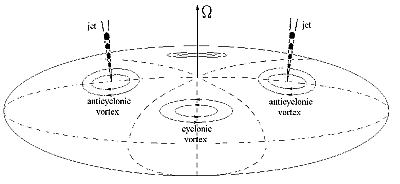
Ris. 2. Shematicheskoe izobrazhenie razvitiya ciklonicheskih i anticiklonicheskih vihrei Rossbi v nekotorom sloe vrashayushegosya massivnogo protozvezdnogo oblaka |
- posle iniciiruyushego processa, kotorym mozhet byt', naprimer,
prohozhdenie holodnym gazovym oblakom fronta galakticheskoi udarnoi
volny, dzhinsovskii masshtab stanovitsya men'she harakternogo masshtaba
oblaka i nachinaetsya gravitacionnoe szhatie poslednego;
- nalichie nachal'nogo summarnogo momenta impul'sa privodit k
vrasheniyu oblaka, vse ubystryayushemusya po mere szhatiya;
- centrobezhnye effekty privodyat k tomu, chto szhatie
vdol' osi vrasheniya proishodit bystree, chem v poperechnoi ploskosti,
iz-za chego oblako prinimaet formu splyusnutogo ellipsoida vrasheniya;
- pri dostizhenii opredelennoi skorosti vrasheniya oblaka chislo
Kibelya-Rossbi okazyvaetsya dostatochno malym dlya poyavleniya v
oblake voln i vihrei Rossbi;
- v vysokih shirotah formiruetsya regulyarnaya struktura ciklonicheskih
i anticiklonicheskih vihrei;
- iz-za povysheniya plotnosti v anticiklonah dzhinsovskii masshtab
lokal'no okazyvaetsya dlya nih men'she, chem dlya okruzhayushei sredy i
sootvetstvenno razvivaetsya lokal'naya gravitacionnaya
neustoichivost';
- razvitie poslednei privodit k obrazovaniyu protozvezd s
anticiklonicheskimi rotorami skorostei, obrazuyushimi drug s drugom malye
ugly;
- na opredelennoi stadii evolyucii protozvezd v silu obshih zakonomernostei, kotorye my obsuzhdali v [1-3], v protozvezdah formiruyutsya dzhety, parallel'nye ih sobstvennym momentam vrasheniya, i realizuetsya situaciya, pokazannaya na ris. 2 (pri etom, veroyatno, skvoz' oblako budet prosvechivat' central'noe yadro, znachitel'no razogretoe gravitacionnym szhatiem).
3![]() . Dlya issledovaniya zakona dispersii vozmushenii
maloi amplitudy rassmotrim protozvezdnoe oblako, obladayushee nekim
summarnym momentom vrasheniya na stadii gravitacionnogo szhatiya,
iz-za chego ego izobary predstavlyayut soboi ellipsoidy vrasheniya.
Takaya konfiguraciya bezuslovno nestacionarna; my, odnako,
predpolagaem, chto harakternoe vremya szhatiya znachitel'no prevyshaet
period vrasheniya oblaka. Osnovaniya nadeyatsya na eto daet tot fakt,
chto protozvezdnye oblaka bogaty metallicheskoi pyl'yu i
sootvetstvenno obladayut bol'shoi opticheskoi tolshei i bol'shim
vremenem vyhoda izlucheniya. Poetomu veroyatnee vsego kollaps takogo
oblaka budet proishodit' ne monotonno vo vremeni, a v pul'siruyushem
rezhime, vo vremya odnoi stadii kotorogo budet proishodit' razogrev
central'nyh oblastei pri prakticheski adiabaticheskom gravitacionnom
szhatii oblaka, iz-za chego v etih oblastyah uvelichitsya dzhinsovskii
masshtab i szhatie zamedlitsya, a na vtoroi stadii sistema budet
ozhidat', kogda izlishek energii budet unesen izlucheniem i
dzhinsovskii masshtab umen'shitsya.
. Dlya issledovaniya zakona dispersii vozmushenii
maloi amplitudy rassmotrim protozvezdnoe oblako, obladayushee nekim
summarnym momentom vrasheniya na stadii gravitacionnogo szhatiya,
iz-za chego ego izobary predstavlyayut soboi ellipsoidy vrasheniya.
Takaya konfiguraciya bezuslovno nestacionarna; my, odnako,
predpolagaem, chto harakternoe vremya szhatiya znachitel'no prevyshaet
period vrasheniya oblaka. Osnovaniya nadeyatsya na eto daet tot fakt,
chto protozvezdnye oblaka bogaty metallicheskoi pyl'yu i
sootvetstvenno obladayut bol'shoi opticheskoi tolshei i bol'shim
vremenem vyhoda izlucheniya. Poetomu veroyatnee vsego kollaps takogo
oblaka budet proishodit' ne monotonno vo vremeni, a v pul'siruyushem
rezhime, vo vremya odnoi stadii kotorogo budet proishodit' razogrev
central'nyh oblastei pri prakticheski adiabaticheskom gravitacionnom
szhatii oblaka, iz-za chego v etih oblastyah uvelichitsya dzhinsovskii
masshtab i szhatie zamedlitsya, a na vtoroi stadii sistema budet
ozhidat', kogda izlishek energii budet unesen izlucheniem i
dzhinsovskii masshtab umen'shitsya.
V silu skazannogo dannaya chast' nashei raboty ne mozhet pretendovat' na matematicheskuyu strogost', dostatochno korrektno rassmatrivaemaya zadacha mozhet byt' reshena lish' metodom evolyucionnogo chislennogo nelineinogo modelirovaniya; osnovnaya cel' nastoyashei zametki - proanalizirovat', imeyutsya li predposylki dlya postanovki takogo modelirovaniya.
Sredu modeliruem nevyazkim szhimaemym samogravitiruyushim
ideal'nym gazom s uravneniem sostoyaniya

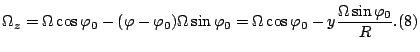

Budem rassmatrivat' dinamiku barotropnyh vozmushenii, ne imeyushih
![]() -struktury (v otlichie ot baroklinnyh - sm. [6]), poskol'ku
nas interesuyut naibolee krupnomasshtabnye vozmusheniya. Formal'noe
osnovanie dlya takoi postanovki zadachi daet tot fakt, chto
vertikal'nyi masshtab izmeneniya «ravnovesnoi» plotnosti oblaka
dlya stepennyh raspredelenii parametrov modeli
-struktury (v otlichie ot baroklinnyh - sm. [6]), poskol'ku
nas interesuyut naibolee krupnomasshtabnye vozmusheniya. Formal'noe
osnovanie dlya takoi postanovki zadachi daet tot fakt, chto
vertikal'nyi masshtab izmeneniya «ravnovesnoi» plotnosti oblaka
dlya stepennyh raspredelenii parametrov modeli
V takoi postanovke zadachi dinamika malyh vozmushenii vida
![]() opredelyaetsya sistemoi
linearizovannyh uravnenii:
opredelyaetsya sistemoi
linearizovannyh uravnenii:
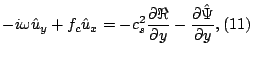
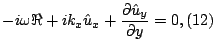

Differenciruya (11) po ![]() , isklyuchaem iz (10) i (11)
, isklyuchaem iz (10) i (11) ![]() i
i
![]() pri pomoshi (13) i (12) sootvetstvenno; poluchaem
pri pomoshi (13) i (12) sootvetstvenno; poluchaem

S drugoi storony, differenciruya (10) po ![]() , isklyuchaem
, isklyuchaem ![]() i
i
![]() pri pomoshi (12):
pri pomoshi (12):

Predpolagaya dalee vozmusheniya dostatochno korotkovolnovymi vdol' meridiana
(
![]() ), ishem reshenie v vide
), ishem reshenie v vide
![]() i, vypisyvaya uslovie sovmestnosti uravnenii (14) i (15), poluchaem
dispersionnoe
uravnenie s tochnost'yu do lineinyh po malomu parametru
i, vypisyvaya uslovie sovmestnosti uravnenii (14) i (15), poluchaem
dispersionnoe
uravnenie s tochnost'yu do lineinyh po malomu parametru
![]() slagaemyh:
slagaemyh:
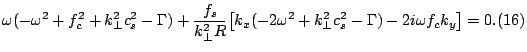
Otmetim, chto poslednee slagaemoe v kvadratnyh skobkah v (16) yavlyaetsya nefizichnym, i ego neobhodimo prosto otbrosit'. Deistvitel'no, poyavlenie v dispersionnom uravnenii fizichnyh mnimyh slagaemyh vozmozhno tol'ko v zadachah s dissipaciei ili vneshnei nakachkoi energii. V dannom zhe sluchae eto yavlyaetsya sledstviem ne vpolne korrektnogo ucheta geometrii zadachi: real'no rasstoyanie mezhdu meridianami umen'shaetsya s priblizheniem k polyusu, iz-za chego, v silu sohraneniya potoka energii v volne, ee amplituda dolzhna pri etom vozrastat', chto ne uchityvaetsya v nashei priblizhennoi postanovke zadachi.
Odnako dazhe s uchetom sdelannogo zamechaniya v predel'nom sluchae
nesamogravitiruyushei sredy (
![]() ) uravnenie (16) ne
perehodit v klassicheskii zakon dispersii voln Rossbi i
gravitacionno-giroskopicheskih voln [5-7], otlichayas' slagaemym
) uravnenie (16) ne
perehodit v klassicheskii zakon dispersii voln Rossbi i
gravitacionno-giroskopicheskih voln [5-7], otlichayas' slagaemym
![]() v poslednei skobke. Eto ne udivitel'no, poskol'ku
(16) polucheno iz uravnenii bolee vysokogo poryadka. Tem ne menee
chislennoe issledovanie pokazyvaet, chto eto slagaemoe v ukazannom
predel'nom sluchae daet popravku vtorogo poryadka malosti kak k
chastote gravitacionno-giroskopicheskih voln, tak i k chastote voln
Rossbi.
v poslednei skobke. Eto ne udivitel'no, poskol'ku
(16) polucheno iz uravnenii bolee vysokogo poryadka. Tem ne menee
chislennoe issledovanie pokazyvaet, chto eto slagaemoe v ukazannom
predel'nom sluchae daet popravku vtorogo poryadka malosti kak k
chastote gravitacionno-giroskopicheskih voln, tak i k chastote voln
Rossbi.
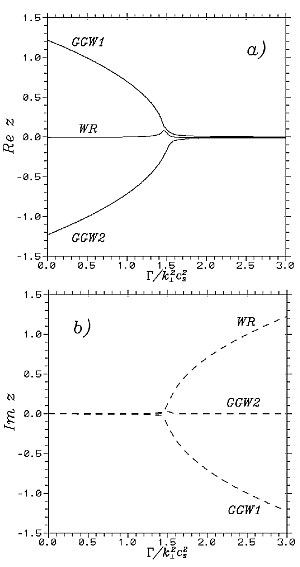 |
Ris. 4.
Zavisimosti otnositel'nyh fazovyh skorostei
|
4![]() . Na ris. 4 my privodim dispersionnye krivye
v zavisimosti ot kvadrata
otnosheniya dliny volny vozmushenii k dzhinsovskomu masshtabu
(
. Na ris. 4 my privodim dispersionnye krivye
v zavisimosti ot kvadrata
otnosheniya dliny volny vozmushenii k dzhinsovskomu masshtabu
(
![]() ).
).
Naibolee vazhnymi dlya nashego rassmotreniya v poluchennyh rezul'tatah yavlyayutsya dva momenta. Vo-pervyh, esli gravitacionno-giroskopicheskie volny (akusticheskaya moda kolebanii) pri prevyshenii kriticheskogo masshtaba Dzhinsa okazyvayutsya libo slabo neustoichivymi, libo zatuhayut, to volny Rossbi (vihrevaya moda kolebanii) obladayut znachitel'noi otnositel'noi skorost'yu rosta amplitudy. Vo-vtoryh, eta skorost' rosta okazyvaetsya sravnimoi so skorost'yu zvuka i sushestvenno prevyshaet fazovuyu skorost' voln Rossbi. V to zhe vremya v [5] pokazano, chto skorost' dreifa nelineinogo paketa anticiklonicheskih voln Rossbi priblizhaetsya k ih fazovoi skorosti, opredelennoi na osnove lineinogo analiza. Takim obrazom, plotnost' v anticiklonicheskih vihryah Rossbi dolzhna narastat' iz-za effektov samogravitacii znachitel'no bystree, chem oni budut smeshat'sya vdol' shiroty iz-za dreifa.
 |
Ris. 5.
Linii urovnei otnositel'nyh skorostei rosta amplitudy
|
K analogichnomu vyvodu pozvolyayut priiti i nashi issledovaniya. Kak sleduet iz ris. 5, opredelyayushaya skorost' dreifa gruppovaya skorost' dlya voln Rossbi men'she ili sravnima s fazovoi skorost'yu etih voln i, sledovatel'no, mnogo men'she kak zvukovoi skorosti, tak i skorosti rosta amplitudy iz-za razvitiya gravitacionnoi neustoichivosti.
Apriorno yasno, chto stol' bystroe razvitie gravitacionnoi
neustoichivosti v lokal'nyh anticiklonicheskih uplotneniyah
ochen'
bystro privedet k narusheniyu rezhima Rossbi: chislo
Kibelya-Rossbi perestanet byt' malym - iz-za tendencii k
sohraneniyu uglovogo momenta v vihryah umen'shayushegosya so vremenem
radiusa i sootvetstvenno raskruchivayushihsya. Tem ne menee,
predstavlyaetsya vpolne veroyatnym, chto takie struktury okazhutsya
dolgozhivushimi (imenno v silu ukazannoi tendencii) i privedut k
obrazovaniyu protozvezd i formirovaniyu dzhetov.
Obobshaya provedennyi analiz, mozhno, veroyatno, utverzhdat', chto lyuboe gazovoe oblako, ispytyvayushee gravitacionnyi kollaps, s neizbezhnost'yu prohodit stadiyu rezhima Rossbi, esli tol'ko ego summarnyi nachal'nyi moment impul'sa ne raven nulyu. Kak predstavlyaetsya, soputstvuyushee etomu processu vozniknovenie znachitel'nyh neodnorodnostei neobhodimo uchityvat' pri rassmotrenii evolyucii astrofizicheskih ob'ektov.
<< 3. Volny Rossbi v diske | Oglavlenie | 5. Effekty Rossbi na Solnce >>