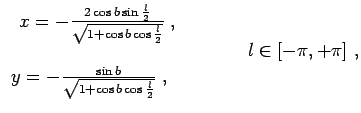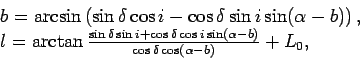<< 3. Rabota s ASCII
| Oglavlenie |
5. Diagramma Gercshprunga-Ressela >>
Razdely
4. Postroenie raspredeleniya zvezd Hipparcos
na nebesnoi sfere i v prostranstve
4.1. Raspredelenie zvezd po nebesnoi sfere
S pomosh'yu Celestia 2000 mozhno postroit' kartinu raspredeleniya vyborki zvezd na nebesnoi sfere v neskol'kih proekciyah. Naibolee populyarnaya iz nih - eto proekciya Hammer-Aitofa, ona byla prinyata v kachestve osnovnoi v opisanii Hipparcos i ispol'zovalas' vo mnogih pervyh publikaciyah. Odnako graficheskie vozmozhnosti Celestia dovol'no ogranicheny. Naprimer, pri chisle zvezd bolee 1000 diagrammy stroyatsya ne tochkami, a zakrashennymi oblastyami, simvoliziruyushimi zvezdnuyu plotnost'. Eto chislo izmenit' nel'zya, a v diagramme s zalitymi oblastyami net legendy, po kotoroi mozhno bylo by ponyat' absolyutnoe znachenie zvezdnoi plotnosti v konkretnom meste. Otsutstvuyut vozmozhnosti vydeleniya cvetom zvezd po kakomu-libo kriteriyu. Po etim i mnogim drugim prichinam u issledovatelya vozniknet potrebnost' v samostoyatel'nom postroenii kartiny raspredeleniya zvezd po nebesnoi sfere.
Sleduyushie formuly opisyvayut proekciyu Hammer-Aitofa dlya sfericheskoi galakticheskoi sistemy koordinat:
zdes'
, 
- galakticheskie koordinaty, vyrazhennye v radianah, prichem dolgotu
sleduet privesti v diapazon [-
,+];
, 
- dekartovy koordinaty na ploskosti; budet nahodit'sya v diapazone [-1,
+1], a - v diapazone [-2, +2], nachalo koordinat (0, 0) sootvetstvuet
napravleniyu na centr Galaktiki.
Napishem programmu, kotoraya stroit izobrazheniya zvezd v etoi proekcii. V
kachestve graficheskoi platformy ispol'zuem standartnuyu biblioteku BGI,
realizaciya kotoroi est' v Borland Pascal, Free Pascal4.1, Borland C++. Ona nastol'ko prosta, chto dazhe
nachinayushii programmist legko adaptiruet programmu, ispol'zuyushuyu BGI, pod
lyubuyu druguyu sistemu. Os' 
v etom rezhime imeet napravlenie sleva napravo, a
os' 
- sverhu vniz. Verhnii levyi ugol imeet koordinaty (0,0), a pravyi
nizhnii (GetMaxX, GetMaxY). Etu sistemu koordinat v nashem izlozhenii my budem
nazyvat' ekrannoi.
Dlya nachala napishem dve procedury Aitoff i Screen. Pervaya budet perevodit' sfericheskie galakticheskie koordinaty v dekartovy po formulam (4.1), a vtoraya - dekartovy v ekrannye.
Listing 4.1. Procedury perevoda koordinat
Procedure Aitoff(
l,b:double; { Sfericheskie koordinaty v
radianah }
var x,y : double); { Dekartovy koordinaty
}
var s : double;
begin
if l>Pi then l:=l-2*Pi;
{ Privedenie l v diapazon -Pi do +Pi }
s:=sqrt(1+cos(b)*cos(l/2)); { Znamenatel' formul
4.1 }
x:=-2*cos(b)*sin(l/2)/s;
y:=sin(b)/s;
end;
Procedure Screen
(x,y : double; { Dekartovy koordinaty }
X0,Y0: integer;{Ekrannye koordinaty nachala
dekartovoi sistemy}
Scale: double;{Masshtab - skol'ko tochek ekrana
na edinicu dliny}
var u,v : integer);{ Ekrannye
koordinaty }
begin
u:=X0+Round(Scale*x);
v:=Y0-Round(Scale*y);
end;
Neskol'ko gromozdkoi mozhet pokazat'sya procedura, otrisovyvayushaya koordinatnuyu setku, no nikakih algoritmicheskih slozhnostei v nei net.
Listing 4.2. Procedura, risuyushaya koordinatnuyu setku.
function rad(x:double):double; {
Perevod gradusov v radiany }
begin
rad:=x/180.0*Pi;
end;
Procedure AitoffGrid
(Step:integer; { Shag setki v gradusah
}
X0,Y0 : integer; { Ekrannye koordinaty centra
proekcii }
Scale : double; { Masshtab - tochek na edinicu
dliny }
Gr : boolean); {Flag - v gradusah ili v chasah
razmetka dolgoty}
var i,j : integer; {
Peremennye ciklov for }
l,b : double; { Galakticheskie
koordinaty }
x,y : double; { Dekartovy koordinaty
}
u,v : integer; { Ekrannye koordinaty
}
s : string[5]; { Stroka dlya podpisei
}
h : integer; { Dlya razmetki osei }
begin
{ Nanesenie setki meridianov }
i:=-180; {Pervyi meridian -180
gradusov }
repeat { Cikl po
meridianam }
l:=rad(i); { Perevod v radiany }
j:=-90; { Pervaya tochka meridiana }
repeat { Cikl postroeniya vdol'
meridiana }
{ Vychislenie tochki meridiana }
b:=rad(j); { Perevod v radiany shiroty
}
Aitoff(l,b,x,y); { Perevod v dekartovy
koordinaty }
Screen(x,y,X0,Y0,scale,u,v); { Perevod v
ekrannye koord. }
{ Esli tochka pervaya (j=-90), to pomeshaem
graficheskii kursor
v tochku (u,v) funkciei MoveTo, esli tochka ne pervaya, to
?procherchivaem? kursorom liniyu iz predydushei tochki
v tochku (u,v) funkciei LineTo }
if j=-90 then MoveTo(u,v) else LineTo(u,v);
j:=j+5; { Shag 5 gradusov obespechivayut gladkii
vid meridiana }
until j>90;
i:=i+step; { Perehod k sleduyushemu
meridianu }
until i>180;
{ Nanesenie setki parallelei - analogichno
predydushemu }
j:=-90;
repeat { cikl po parallelyam
}
b:=rad(j);
i:=-180;
repeat { cikl postroeniya
vdol' paralleli }
l:=rad(i);
Aitoff(l,b,x,y);
Screen(x,y,X0,Y0,scale,u,v);
if i=-180 then MoveTo(u,v) else LineTo(u,v);
i:=i+5;
until i>180;
j:=j+step;
until j>90;
{ Zadanie svoistv shrifta (mozhet zaviset' ot
graf.bibl.) }
SetTextStyle(DefaultFont,HorizDir,1);
SetTextJustify(LeftText,BottomText);
{ Podpisi meridianov vdol' ekvatora
}
i:=-180;
repeat
{ Vychislenie koordinaty tochki vyvoda
nadpisi }
l:=Rad(i);
Aitoff(l,0,x,y);
Screen(x,y,X0,Y0,scale,u,v);
{ Esli Gr istina, to razmetka v gradusah, inache
- v chasah }
if Gr then h:=i
elsebegin h:=i div 15;
if h<0 then h:=h+24;
end;
Str(h,s); { Preobrazovanie znacheniya h v
tekstovuyu stroku }
OutTextXY(u+5,v-5,s); { Vyvod tekstovoi stroki
}
i:=i+step; { Perehod k sleduyushemu
meridianu }
until i>180;
{ Izmenenie vyravnivaniya teksta }
SetTextJustify(RightText,BottomText);
{ Podpisi parallelei vdol' nulevogo meridiana -
analogichno }
j:=-90+step;
repeat
if j<>0 then {
Ekvator ne podpisyvaem }
begin
b:=Rad(j);
Aitoff(0,b,x,y);
Screen(x,y,X0,Y0,scale,u,v);
Str(j,s);
OutTextXY(u-5,v-5,s);
end;
j:=j+step;
until j>90-step;
end;
Esli my hotim postroit' proekcii zvezd Hipparcos v galakticheskoi sisteme koordinat, to nam neobhodimo perevesti ekvatorial'nye koordinaty, privedennye v kataloge, v galakticheskie. Eto mozhno sdelat' po formulam
a listing 4.3 predstavlyaet realizaciyu etih formul.
Zdes'
- ekvatorial'nye koordinaty;
= 62
52' 18.295? - naklon galakticheskogo ekvatora;
51' 34.131? 
dolgota voshodyashego uzla
galakticheskogo ekvatora;
L
= 32 55' 54.905? - dolgota napravleniya na centr Galaktiki;
- galakticheskie koordinaty.
Znacheniya konstant privedeny na epohu J1991.25. Vo vtoroi formule
podrazumevaetsya krugovoi arktangens - chislitel' interpretiruetsya kak sinus ugla, a znamenatel'
- kak kosinus.
V standartnoi biblioteke Pascal mogut otsutstvovat' funkcii arcsin, arctan2, poetomu my
sochli celesoobraznym takzhe pomestit' zdes' kod etih funkcii.
Listing 4.3. Perevod ekvatorial'nyh koordinat v galakticheskie
Function ArcTan2(x,y:double):double;
var z:double;
begin
if y<>0 then
z:=arctan(x/y)
else z:=Pi/2;
if y<0 then z:=z+Pi;
ArcTan2:=z;
end;
Function ArcSin(x:double):double;
begin
ArcSin:=ArcTan2(x,sqrt(1-sqr(x)));
end;
Procedure Galaxy(a,d : double;
var l,b : double);
Var sa,ca,sd,cd : double;
Const Leo = 4.936829261; {
282.85948083}
L0 = 0.57477039907; { 32.931918056 }
si = 0.88998807641; { sin 62.871748611 }
ci = 0.45598379779; { cos 62.871748611 }
begin
a:=a-Leo;
sa:=sin(a); ca:=cos(a);
sd:=sin(d); cd:=cos(d);
b:=arcsin(sd*ci-cd*si*sa);
l:=arctan2(sd*si+cd*ci*sa,cd*ca)+L0;
end;
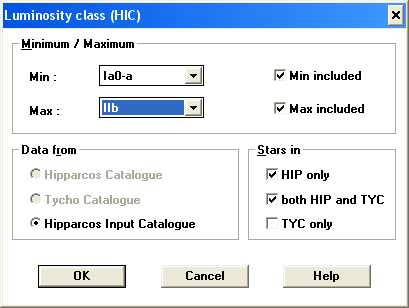
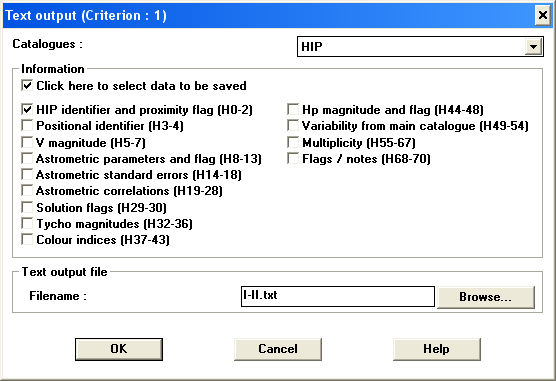
Nakonec, pereidem k glavnoi programme. Reshim takuyu zadachu: otobrazit' raspredelenie zvezd po nebesnoi sfere I i II klassa svetimosti, prichem zvezdy spektral'nyh klassov O, B vydelit' sinim cvetom, A - golubym, F, G - zheltym, K, M - krasnym. Dlya otbora zvezd ispol'zuem programmu Celestia i vyberem zvezdy s klassom svetimosti ot Ia0-a do IIb (ris. 4.1). Vsego dolzhno byt' naideno 2248 zvezd. Sohranim vyborku (Sample) v fail I-II.txt (ris. 4.2).
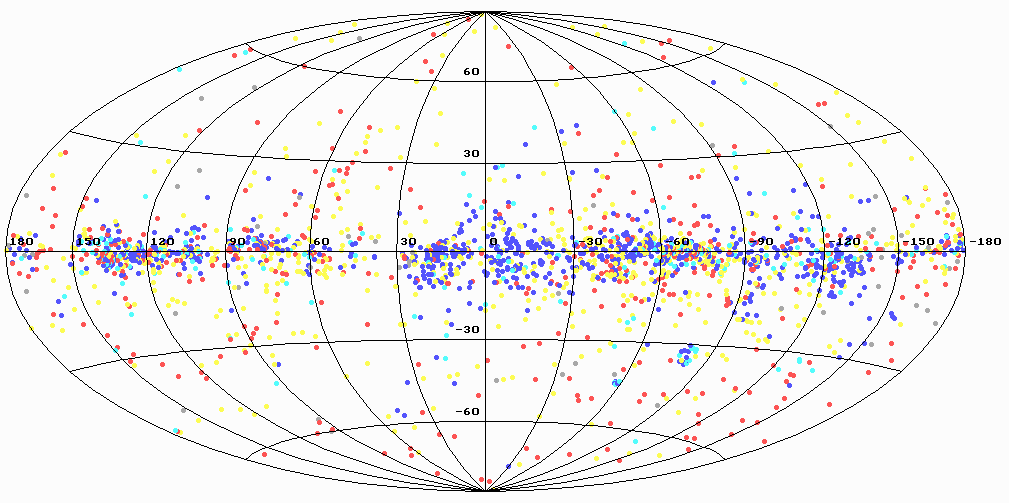
Tekst programmy, vypolnyayushei postroenie raspredelenie zvezd po nebesnoi sfere, priveden v listinge 4.4, a rezul'tat ee raboty - na ris. 4.3.
V osnovnom cikle while proishodit chtenie dannyh o zvezde, proverka, udovletvoryaet li zvezda kriteriyu otbora, opredelenie cveta vyvoda tochki v operatore case. Dalee proishodit preobrazovanie koordinat v galakticheskie, zatem v dekartovy koordinaty proekcii i v ekrannye koordinaty. Dlya prostoty izlozheniya my stavim tochku proceduroi PutPixel, no mozhno narisovat' i druguyu geometricheskuyu figuru (romb, krug).
Listing 4.4. Postroenie raspredeleniya zvezd po nebesnoi sfere
Program Picture;
Uses Graph, HipMain, Projection;
{ V modul' Projection sobrany vse predydushie podprogrammy }
var s : THipparcos;
driver,mode : integer; { Dlya inicializacii grafich. rezhima }
color : integer; { Cvet tochki }
l, b : double; { Galakticheskie koordinaty }
x, y : double; { Dekartovy koordinaty }
u, v : integer; { Ekrannye koordinaty }
CX, CY : integer;{ Ekrannye koordinaty centra proekcii }
SC : integer;{Masshtab perevoda dekartovyh koord. v ekrannye}
begin
{ Inicializaciya graficheskogo rezhima }
Driver:=detect; Mode:=0; InitGraph(Driver,Mode,'D:/BP/BGI');
{ Zadanie masshtaba i centra }
{ Proekciya Aitofa imeet X v diapazone ot -2 do 2, i zazor }
SC:=GetMaxX div 4 -10;
CX:=GetMaxX div 2; CY:=GetMaxY div 2;
AitoffGrid(30,CX,CY,SC,True); { Vyvod setki koordinat }
OpenHipparcosMain; { Otkrytie kataloga i }
InitCriteria('I-II.txt'); { inicializaciya kriteriya }
while ReadHipparcosMain(s) do { Cikl chteniya zvezd }
if inCelestia(s.HIP) then { Proverka kriteriya }
begin
case s.SP[0] of { Opredelenie cveta zvezdy }
'O','B': color:=LightBlue;
'A' : color:=LightCyan;
'F','G': color:=Yellow;
'K','M': color:=LightRed;
else color:=LightGray;
end; { case }
{ Perevod ekvatorial'nyh koordinat v radiany, a zatem
v galakticheskie koordinaty }
Galaxy(rad(s.RADeg),rad(s.DEDeg),l,b);
{ Vychislenie dekartovyh koordinat proekcii Aitofa }
Aitoff(l,b,x,y);
Screen(x,y,CX,CY,SC,u,v); { Perevod v ekrannye koordinaty }
PutPixel(u,v,color);{Postavit' tochku (mozhno zamenit' na krug)}
end; { if i while }
ClearCriteria;
CloseHipparcosMain;
end.
4.2. Raspredelenie zvezd v prostranstve
Znanie parallaksov daet vozmozhnost' poluchit' vse tri prostranstvennyh koordinaty zvezdy kataloga Hipparcos. S pomosh'yu neslozhnyh programm mozhno postroit' vizualizaciyu zadannoi vyborki zvezdy v prostranstve.
Naprimer, postroim raspredelenie v prostranstve zvezd spektral'nyh klassov
O-B5, kotorye nahodyatsya k nam blizhe 500 pk i imeyut otnositel'nuyu tochnost'
opredeleniya parallaksa luchshe, chem 50%. Listing 4.5 formiruet tekstovyi
fail, gde v tri kolonki idut pryamougol'nye galakticheskie koordinaty zvezd
, , 
.
Hotya zadachu vizualizacii takogo massiva mozhno realizovat' i samostoyatel'no,
no dlya resheniya podobnogo roda zadach sushestvuet bol'shoe chislo matematicheskih
programm. My vospol'zuemsya populyarnoi i dostatochno prostoi v osvoenii
programmoi MathCAD (goditsya lyubaya versiya starshe 6.0). Vid ekrana programmy
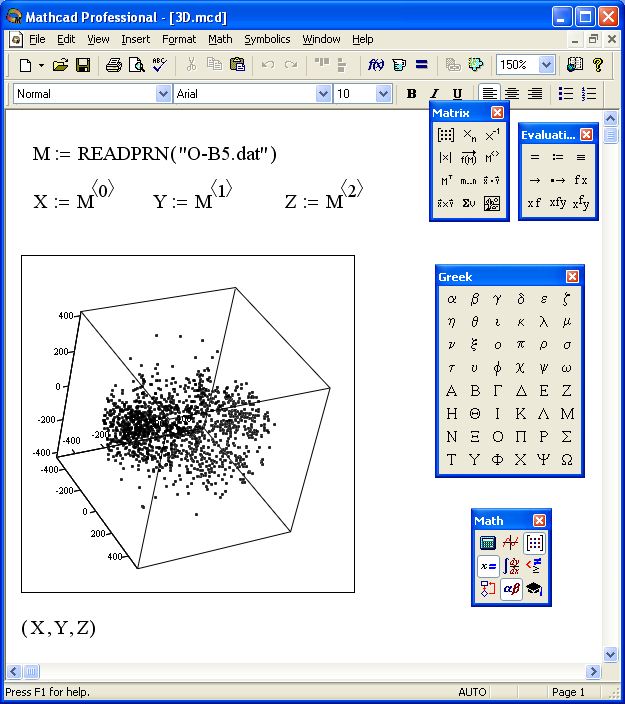
MathCAD vmeste s tekstom postroeniya tochechnogo grafika predstavlen na
ris. 4.4. Pervyi operator M:=READPRN(?O-B5.DAT?) schityvaet v matricu M
soderzhimoe faila, sformirovannogo nashei programmoi. Posleduyushie tri
operatora zadayut tri vektora, kotorye yavlyayutsya stolbcami etoi matricy. Dalee
s pomosh'yu komandy menyu Insert-Graph-3D Scatter Plot my stroim neobhodimuyu kartinu raspredeleniya zvezd v
prostranstve, s kotoroi mozhno proizvodit' raznye operacii: vrashenie,
izmenenie masshtaba, perspektivy, dobavlenie "tumana" i pr.
Listing 4.5. Formirovanie pryamougol'nyh koordinat zvezd
Program Plot3D;
Uses HipMain,Projection;
Const Criteria = 'O-B5'; { Imya
faila kriteriya }
n : integer = 0; { Schetchik }
var s : THipparcos;
r : double; { Rasstoyanie }
l, b : double; { Galakticheskie
koordinaty }
x,y,z : double; { Dekartovy galakticheskie
koordinaty }
f : text; { Fail vyvoda rezul'tatov
}
begin
{ Vyhodnoi fail imeet rasshirenie .DAT
}
assign(f,Criteria+'.DAT'); Rewrite(f);
OpenHipparcosMain;
{ Fail spiska zvezd imeet rasshirenie
.TXT }
writeln(InitCriteria(Criteria+'.txt'),' zvezd v kriterii.');
while ReadHipparcosMain(s) do
begin
{ net dannyh o parallakse }
if (s.info and NoPlx)<>0
then continue;
{ "plohoe" znachenie parallaksa }
if s.plx<=0.0 then
continue;
{ nizkaya tochnost' parallaksa }
if s.sigma.plx/s.plx>0.5
then continue;
if inCelestia(s.HIP) then
begin
r:=1000.0/s.plx; { Vychislenie rasstoyaniya v
pk }
if r>500.0 then continue; { Otbros dalekih zvezd
}
{ Perevod v galakticheskie koordinaty
}
Galaxy(rad(s.RADeg),rad(s.DEDeg),l,b);
x:=r*cos(b)*cos(l); { Vychislenie
pryamougol'nyh }
y:=r*cos(b)*sin(l); { galakticheskih
koordinat }
z:=r*sin(b);
writeln(f,x:10:2,y:10:2,z:10:2); { Vyvod v
fail }
inc(n); { Uvelichenie schetchika na
edinicu }
end; { if }
end; { while }
ClearCriteria;
CloseHipparcosMain;
Close(f);
writeln(n,' zvezd obrabotano.');
end.
<< 3. Rabota s ASCII | Oglavlenie | 5. Diagramma Gercshprunga-Ressela >>
|
Publikacii s klyuchevymi slovami:
astrometriya - katalogi - Hipparcos
Publikacii so slovami: astrometriya - katalogi - Hipparcos | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
