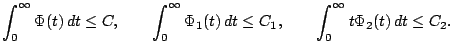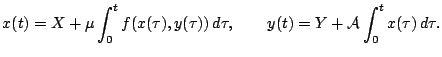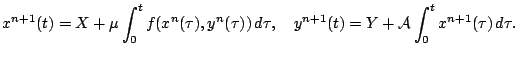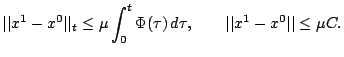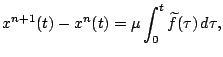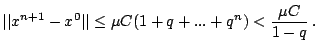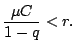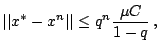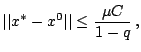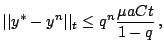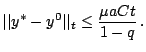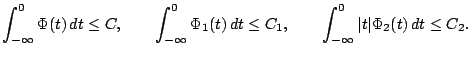<< 1. Vvedenie | Oglavlenie | 3. Razlet bez sblizhenii >>
2. Osnovnaya teorema
Slabovozmushennaya zadacha neskol'kih tel v podhodyashih peremennyh mozhet byt' predstavlena sistemoi obyknovennyh differencial'nyh uravnenii sleduyushego vida [19]:
Zdes'
Uprostim sistemu (3). Vo-pervyh, primem ![]() za novye
medlennye peremennye. Etogo vsegda mozhno dobit'sya, dobaviv
za novye
medlennye peremennye. Etogo vsegda mozhno dobit'sya, dobaviv ![]() k
vektoru
k
vektoru ![]() i uvelichiv tem samym poryadok sistemy uravnenii. Esli zhe
i uvelichiv tem samym poryadok sistemy uravnenii. Esli zhe
![]() vzaimno-odnoznachno zavisit ot
vzaimno-odnoznachno zavisit ot ![]() komponent vektora
komponent vektora ![]() , to
mozhno ne uvelichivat' chisla peremennyh.
Vo-vtoryh, obratim v nul' vektor
, to
mozhno ne uvelichivat' chisla peremennyh.
Vo-vtoryh, obratim v nul' vektor ![]() . Tut pridetsya uvelichit' chislo
medlennyh peremennyh. Dlya kazhdogo
. Tut pridetsya uvelichit' chislo
medlennyh peremennyh. Dlya kazhdogo ![]() , dlya kotorogo
, dlya kotorogo ![]() ,
vvedem novuyu medlennuyu peremennuyu
,
vvedem novuyu medlennuyu peremennuyu ![]() i zamenim
i zamenim ![]() na
na
![]() :
:
V rezul'tate dvuh preobrazovanii uravneniya primut formu
Zdes'
gde na glavnoi diagonali pryamougol'noi matricy
V dal'neishem imeem delo tol'ko s sistemoi vida (5).
Funkcii ![]() schitaem nepreryvnymi i udovletvoryayushimi usloviyu Lipshica
v oblasti
schitaem nepreryvnymi i udovletvoryayushimi usloviyu Lipshica
v oblasti
![]() ,
k postroeniyu kotoroi my pristupaem.
,
k postroeniyu kotoroi my pristupaem.
V prostranstvah
![]() i
i
![]() vvedem
normy, kotorye budem oboznachat' edinym simvolom
vvedem
normy, kotorye budem oboznachat' edinym simvolom ![]() , chto
ne privodit k putanice. Oni induciruyut normu v
, chto
ne privodit k putanice. Oni induciruyut normu v
![]() i rasstoyaniya v etih treh
prostranstvah. Dlya vektor-funkcii
i rasstoyaniya v etih treh
prostranstvah. Dlya vektor-funkcii ![]() ,
,
![]() ,
vvedem normu
,
vvedem normu ![]() pri fiksirovannom
pri fiksirovannom ![]() i ravnomernuyu normu:
i ravnomernuyu normu:
Pust'
![]() - dekartovo proizvedenie
vypuklyh kompaktov
- dekartovo proizvedenie
vypuklyh kompaktov
![]() i
i
![]() . Vvedem virtual'noe vremya
. Vvedem virtual'noe vremya
![]() . Tak kak sistema (5) avtonomna, za nachalo
otscheta vremeni mozhno vzyat' epohu
. Tak kak sistema (5) avtonomna, za nachalo
otscheta vremeni mozhno vzyat' epohu ![]() . Nashi postroeniya legche
provodit' dlya polutraektorii, pochemu my i ogranichilis' budushim.
Proshloe v avtonomnoi sisteme obladaet temi zhe svoistvami, a nuzhnoe
vposledstvii ob'edinenie proshlogo i budushego legkovypolnimo.
Rassmotrim mnozhestvo
. Nashi postroeniya legche
provodit' dlya polutraektorii, pochemu my i ogranichilis' budushim.
Proshloe v avtonomnoi sisteme obladaet temi zhe svoistvami, a nuzhnoe
vposledstvii ob'edinenie proshlogo i budushego legkovypolnimo.
Rassmotrim mnozhestvo ![]() - dekartovo proizvedenie mnozhestva
nepreryvnyh na
- dekartovo proizvedenie mnozhestva
nepreryvnyh na
![]() funkcii
funkcii ![]() so znacheniyami v
so znacheniyami v
![]() i mnozhestva postoyannyh
i mnozhestva postoyannyh
![]() takih, chto
takih, chto
![]() pri kazhdom
pri kazhdom ![]() . Za
. Za
![]() primem mnozhestvo tochek iz
primem mnozhestvo tochek iz
![]() , predstavimyh v vide
, predstavimyh v vide
![]() pri
pri
![]() i fiksirovannom
i fiksirovannom
![]() . Oboznacheniya soglasovany:
. Oboznacheniya soglasovany: ![]() pri
pri ![]() .
Za
.
Za ![]() primem ob'edinenie
primem ob'edinenie
![]() po vsem
po vsem
![]() .
.
Soglasno lemmam 1, 2 (s uchetom vypuklosti dekartova
proizvedeniya vypuklyh mnozhestv) ![]() i
i ![]() vypukly i sovpadayut
s mnozhestvom tochek, predstavimyh v vide
vypukly i sovpadayut
s mnozhestvom tochek, predstavimyh v vide
![]() pri
pri
![]() , pri fiksirovannom
, pri fiksirovannom ![]() i pri vseh
i pri vseh ![]() sootvetstvenno. Eto - klyuchevoi moment dlya dal'neishego. Hotya my ne
znaem povedeniya traektorii sistemy (5) kak funkcii real'nogo
vremeni, my ustanavlivaem oblast', v kotoroi oni nahodyatsya, issleduya
zavisimost' fazovyh koordinat kak lineinyh funkcii virtual'nogo
vremeni.
sootvetstvenno. Eto - klyuchevoi moment dlya dal'neishego. Hotya my ne
znaem povedeniya traektorii sistemy (5) kak funkcii real'nogo
vremeni, my ustanavlivaem oblast', v kotoroi oni nahodyatsya, issleduya
zavisimost' fazovyh koordinat kak lineinyh funkcii virtual'nogo
vremeni.
V obshem sluchae naidutsya nachal'nye dannye iz ![]() takie, chto
otvechayushaya im polutraektoriya pokinet
takie, chto
otvechayushaya im polutraektoriya pokinet ![]() . Chtoby etogo ne sluchilos',
suzim oblast' nachal'nyh dannyh do
. Chtoby etogo ne sluchilos',
suzim oblast' nachal'nyh dannyh do
![]() ,
gde
,
gde ![]() - mnozhestvo tochek iz
- mnozhestvo tochek iz ![]() , otstoyashih ot granicy
, otstoyashih ot granicy
![]() ne menee, chem na
ne menee, chem na ![]() ,
, ![]() . Po
lemme 3
. Po
lemme 3 ![]() - vypuklyi kompakt. Dlya nepustoty
- vypuklyi kompakt. Dlya nepustoty ![]() potrebuem
potrebuem
gde
Teper' my v sostoyanii sformulirovat' osnovnuyu teoremu.
Teorema 1. Dana sistema (5) s nepreryvnoi i udovletvoryayushei
usloviyu Lipshica v ![]() funkciei
funkciei ![]() .
Schitaem
.
Schitaem ![]() funkciei virtual'nogo vremeni
funkciei virtual'nogo vremeni
![]() posredstvom
posredstvom
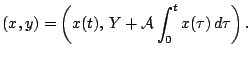
Pust' pri kazhdom ![]() i lyubom vybore
i lyubom vybore
![]() , takih,
chto
, takih,
chto
![]() ,
,
![]() ,
spravedlivy neravenstva
,
spravedlivy neravenstva
prichem mazhoranty dopuskayut integral'nye ocenki
Togda pri vseh polozhitel'nyh ![]() , podchinennyh usloviyu
(6), i
, podchinennyh usloviyu
(6), i
1) resheniya sistemy (5) s nachal'nymi dannymi iz ![]() prodolzhimy na vsyu poluos'
prodolzhimy na vsyu poluos' ![]() i ne vyhodyat iz
i ne vyhodyat iz ![]() ,
prinadlezha
,
prinadlezha ![]() pri kazhdom
pri kazhdom ![]() ;
;
2) resheniya, nachinayushiesya v ![]() , mozhno naiti, ispol'zuya
iteracii, shodyashiesya so skorost'yu geometricheskoi progressii;
shodimost' k
, mozhno naiti, ispol'zuya
iteracii, shodyashiesya so skorost'yu geometricheskoi progressii;
shodimost' k ![]() ravnomerna otnositel'no nachal'nyh dannyh i vremeni
na mnozhestve
ravnomerna otnositel'no nachal'nyh dannyh i vremeni
na mnozhestve
![]() , shodimost' k
, shodimost' k ![]() ravnomerna na mnozhestve
ravnomerna na mnozhestve
![]() pri lyubom
pri lyubom ![]() ;
;
3) pri
![]() peremennye
peremennye ![]() stremyatsya k postoyannym;
stremyatsya k postoyannym;
4) esli predel vektora ![]() otlichen ot nulya, to vektor
otlichen ot nulya, to vektor ![]() pri
pri
![]() stremitsya k lineinoi funkcii vremeni.
stremitsya k lineinoi funkcii vremeni.
Poyasnim smysl chetvertogo utverzhdeniya. Oboznachim
Dokazatel'stvo. Zamenim (5) s nachal'nymi dannymi
![]() pri
pri ![]() ravnosil'noi sistemoi integral'nyh uravnenii
ravnosil'noi sistemoi integral'nyh uravnenii
Obrazuem posledovatel'nost' priblizhenii pikarovskogo tipa. Za nachal'noe voz'mem integriruemyi sluchai
Indeks sverhu vsegda oboznachaet nomer priblizheniya, snizu - nomer komponenty.
Nulevoe priblizhenie s nachal'nymi dannymi iz
![]() s ochevidnost'yu ne vyhodit iz
s ochevidnost'yu ne vyhodit iz ![]() .
.
Pereidem k pervomu priblizheniyu.
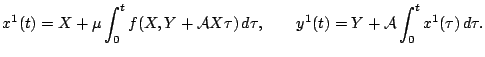
Vsledstvie (9) imeem
Dalee deistvuem po indukcii, predpolagaya
![]() pri
pri
![]() .
Soglasno (12)
.
Soglasno (12)
gde
Analogichno (14) imeem
Podstavlyaya (17) v (16), a rezul'tat - v (15), poluchim s uchetom (8)
gde
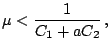
Slozhenie neravenstv (19) pozvolyaet zapisat'
Neravenstvo (9) vlechet
Poetomu pri lyubyh
Oboznachim cherez
![]() predely
predely
![]() pri
pri
![]() . Dokazatel'stvo togo, chto predely sushestvuyut,
predstavlyayut soboi reshenie (5) i spravedlivy pervye dva
utverzhdeniya teoremy, povtoryaet dokazatel'stvo klassicheskoi teoremy
Pikara-Lindelefa [18]. Privedem lish' neskol'ko poleznyh
formul:
. Dokazatel'stvo togo, chto predely sushestvuyut,
predstavlyayut soboi reshenie (5) i spravedlivy pervye dva
utverzhdeniya teoremy, povtoryaet dokazatel'stvo klassicheskoi teoremy
Pikara-Lindelefa [18]. Privedem lish' neskol'ko poleznyh
formul:
Sopostavlenie (7, 8, 10) pokazyvaet, chto sushestvuet konechnyi predel
Pust' ![]() . Soglasno (10) predstavim
. Soglasno (10) predstavim ![]() dlya
dostatochno bol'shih
dlya
dostatochno bol'shih ![]() v vide
v vide
![]() ,
gde
,
gde
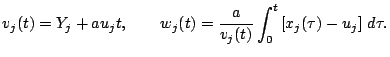
Togda
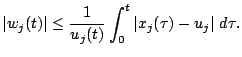
Teorema dokazana.
Zamechanie. Issleduemye v mehanike uravneniya
dvizheniya, kak pravilo, invariantny otnositel'no peremeny znaka
vremeni. Sistema (5) perehodit v sebya pri podstanovke
![]() . Poetomu teorema
1 ostaetsya spravedlivoi i dlya proshlogo pri estestvennyh izmeneniyah
uslovii. Imenno, oboznachim oblasti
. Poetomu teorema
1 ostaetsya spravedlivoi i dlya proshlogo pri estestvennyh izmeneniyah
uslovii. Imenno, oboznachim oblasti ![]() cherez
cherez
![]() , a analogichnye oblasti, zametaemye polutraektoriyami pri
, a analogichnye oblasti, zametaemye polutraektoriyami pri
![]() , cherez
, cherez
![]() . Dokazannye svoistva
. Dokazannye svoistva
![]() perenosyatsya i na
perenosyatsya i na
![]() ,
prichem
,
prichem
![]() . Dlya spravedlivosti
teoremy 1 pri otricatel'nyh
. Dlya spravedlivosti
teoremy 1 pri otricatel'nyh ![]() s ochevidnymi pereformulirovkami
nado lish' zamenit' (8) na
s ochevidnymi pereformulirovkami
nado lish' zamenit' (8) na
Oboznachim cherez ![]() ob'edinenie
ob'edinenie
![]() .
Ochevidno,
.
Ochevidno,
![]() pri
pri
![]() pri
pri
![]() . Utverzhdenie teoremy 1 ostaetsya spravedlivym
s sootvetstvuyushimi pereformulirovkami pri
. Utverzhdenie teoremy 1 ostaetsya spravedlivym
s sootvetstvuyushimi pereformulirovkami pri
![]() ,
esli v (24) zamenit' predely integrirovaniya na
,
esli v (24) zamenit' predely integrirovaniya na
![]() .
Zametim tol'ko, chto beskonechnaya v obe storony oblast'
.
Zametim tol'ko, chto beskonechnaya v obe storony oblast' ![]() uzhe ne budet v obshem sluchae vypukloi, chto ne sushestvenno:
igraet rol' tol'ko vypuklost'
uzhe ne budet v obshem sluchae vypukloi, chto ne sushestvenno:
igraet rol' tol'ko vypuklost' ![]() .
.
<< 1. Vvedenie | Oglavlenie | 3. Razlet bez sblizhenii >>
|
Publikacii s klyuchevymi slovami:
Nebesnaya mehanika - zadacha n-tel - zadacha treh tel
Publikacii so slovami: Nebesnaya mehanika - zadacha n-tel - zadacha treh tel | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |