<< 4. Integriruemost' | Oglavlenie | 4.2. Regional'naya integriruemost' zadachi >>

4.1. Osnovnaya teorema o sushestvovanii integralov

Pust'  - nepustye oblasti prostranstva . Rassmotrim zadachu Koshi s nachal'nymi dannymi iz :

gde  - funkciya gladkosti . Reshenie ( ) oboznachim .

Teorema 5. Pust' resheniya sistemy (47) opredeleny pri vseh i ne vyhodyat iz ; sushestvuet funkciya gladkosti i postoyannaya takie, chto

gde . Togda sushestvuet invariantnaya oblast' , v kotoroi sushestvuet nabor nezavisimyh avtonomnyh integralov gladkosti .

Sut' usloviya (48) svoditsya k sleduyushemu. Hotya otdel'naya traektoriya sistemy (47) ne imeet samoperesechenii, skol' ugodno uzkaya trubka traektorii samoperesekat'sya mozhet. A eto - prepyatstvie k integriruemosti [9]. Uslovie (48) govorit o tom, chto po krainei mere v odnom napravlenii trubka dvizhetsya bez vozvrashenii nazad i poetomu izbegaet samoperesechenii.

Dokazatel'stvo. Oboznachim

Ochevidno,  - invariantnaya otnositel'no potoka sistemy (47) oblast', prichem  - otobrazhenie gladkosti oblasti na ;  - otobrazhenie gladkosti oblasti na , prichem (48) spravedlivo dlya vseh . Zapishem gruppovoe svoistvo otobrazheniya :

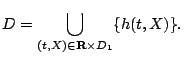
V chastnosti,

V silu (48) uravnenie

imeet otnositel'no edinstvennoe reshenie

pri lyubyh . Po teoreme o neyavnoi funkcii imeet gladkost' . Po opredeleniyu i soglasno (50)      , chto v sopostavlenii s (51) i (52) daet . Podstavlyaya v (50), poluchim

Itak, pri lyubom fiksirovannom pravaya chast' (53) ne menyaetsya vdol' reshenii (47). Kak uzhe otmechalos',  - otobrazhenie na . Poetomu otobrazhenie :

est' integral sistemy (47) gladkosti .

My postroili nabor skalyarnyh integralov - komponent otobrazheniya . Ostalos' dokazat', chto sredi nih rovno nezavisimyh. Eto sleduet iz ochevidnogo svoistva funkcii (54): est' otobrazhenie orbit, t. e.

togda i tol'ko togda, kogda sushestvuet takoe , chto .

Teorema dokazana.

Vsyakaya orbita po obshei teorii diffeomorfna tochke, okruzhnosti ili pryamoi. V silu (52) vremya odnoznachno opredelyaetsya polozheniem, poetomu kazhdaya orbita uravnenii (47) v diffeomorfna pryamoi. Koncy ee otdeleny drug ot druga v silu (48).

---

<< 4. Integriruemost' | Oglavlenie | 4.2. Regional'naya integriruemost' zadachi >>

Publikacii s klyuchevymi slovami: Nebesnaya mehanika - zadacha n-tel - zadacha treh tel Publikacii so slovami: Nebesnaya mehanika - zadacha n-tel - zadacha treh tel

Sm. takzhe: Saimon N'yukom (1835 -1909) k 175-letiyu so dnya rozhdeniya. Naum Il'ich Idel'son - 125 let so dnya rozhdeniya Metody teorii special'nyh vozmushenii v nebesnoi mehanike K 90-letiyu Aleksandra Aleksandrovicha Orlova Dinamika zvezdnyh skoplenii Prosteishaya forma predstavleniya gradienta gravitacionnogo potenciala nebesnyh tel Evolyuciya elementov orbit Yupitera i Saturna na dlitel'nyh intervalah vremeni Vse publikacii na tu zhe temu >>