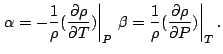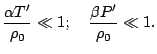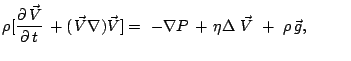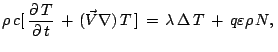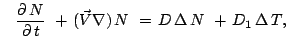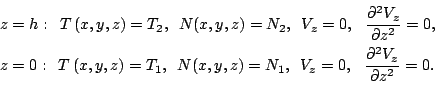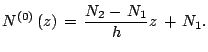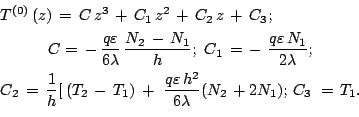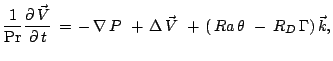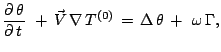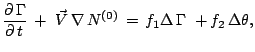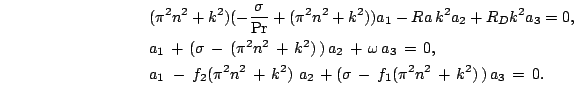<< 2. Uravneniya konvekcii | Oglavlenie | 4. Modelirovanie razvitoi konvekcii >>

3. Usloviya vozniknoveniya konvekcii v mantii

Voznikaet vopros: a pri kakih usloviyah v sisteme, povedenie kotoroi kontroliruetsya gravitacionnym polem i vnutrennimi istochnikami energii, kak eto yavno sleduet iz (3)-(6), vozmozhno stacionarnoe mehanicheskoe ravnovesie? Esli my budem rassmatrivat' sfericheskii sloi, moshnost' kotorogo mnogo men'she radiusa Zemli, , t. e. pri , sferichnost'yu mozhno prenebrech' i sloi rassmatrivat' kak ploskii. Sovmestim koordinatnuyu ploskost' dekartovoi sistemy koordinat s nizhnei granicei sloya. Os' napravim vdol' vektora .

Dlya togo chtoby v yavnom vide vypisat' (3)-(6) kak sistemu, nam neobhodimo ispol'zovat' uravnenie sostoyaniya . Poskol'ku dazhe sostav vnutrennih obolochek ocenen dostatochno grubo, to dlya sloya mantii v kachestve uravneniya sostoyaniya mozhno ispol'zovat' priblizhenie

Sledovatel'no, predpolagaetsya, chto moshnost' sloya dostatochno mala dlya togo, chtoby mozhno bylo prinyat', chto raspredeleniya temperatury, davleniya i plotnosti horosho opisyvayutsya ih srednimi znacheniyami, kotorye my oboznachim , , , a otkloneniya mozhno schitat' malymi po sravneniyu s etimi srednimi v tom smysle, chto

Togda v stacionarnom sostoyanii mehanicheskogo ravnovesiya (3)-(4) dayut

Uravnenie (9) nazyvayut usloviem raspredeleniya gidrostaticheskogo davleniya v zhidkosti. Vzyav ot obeih chastei etogo uravneniya, poluchim vazhnoe sledstvie

t. e. v odnorodnom gravitacionnom pole gidrostaticheski raspredelennaya plotnost' mozhet izmenyat'sya tol'ko vdol' vektora , t. e. osi (u nas ne vrashayushayasya sistema koordinat!). Itak, esli raspredeleniya temperatury, davleniya i plotnosti udovletvoryayut usloviyam (9)-(10), a oni sovmestimy s granichnymi usloviyami, to sistema mozhet nahodit'sya v stacionarnom sostoyanii mehanicheskogo ravnovesiya.

Vopros zaklyuchaetsya v tom, yavlyaetsya li eto sostoyanie ustoichivym ili proizvol'nye, dazhe malye vozmusheniya mogut vyvesti sistemu iz mehanicheskogo ravnovesiya. My imeem delo s issledovaniem problemy ustoichivosti sistemy. Sostoyanie sistemy, harakterizuyusheesya naborom termodinamicheskih parametrov , nazyvayut ustoichivym po Lyapunovu [7], esli dlya lyubogo sushestvuet takoe, chto

zdes'  - proizvol'naya funkciya, opisyvayushaya izmenenie sostoyaniya . Naibolee shiroko na praktike dlya issledovaniya ustoichivosti termodinamicheskogo sostoyaniya sistemy primenyaetsya metod normal'nyh mod [8]. Ego ispol'zovanie my proillyustriruem na primere izucheniya ustoichivosti sostoyaniya mehanicheskogo ravnovesiya dvuhkomponentnoi sistemy, s odnim iz komponentov kotoroi, dlya opredelennosti bolee plotnym, svyazany radioaktivnye istochniki tepla. Zadacha vpervye byla rassmotrena v [9]. Zde' my privedem neskol'ko modificirovannyi i uproshennyi variant resheniya.

Dlya uprosheniya zadachi primem shiroko ispol'zuemoe v geodinamike priblizhenie Bussineska, [8], v kotorom izmenenie plotnosti uchityvaetsya tol'ko v uravnenii balansa impul'sa (3), a v ostal'nyh uravneniyah sistemy prinimaetsya postoyannoi. Togda iz uravneniya (6) sleduet (priblizhenie neszhimaemoi zhidkosti), i v uravnenii (3) tretii chlen v pravoi chasti obrashaetsya v nul'. Posle standartnyh preobrazovanii [4, 8] uravnenie dlya balansa entropii pri dopolnitel'nom uslovii

sushestvenno uprostitsya i mozhno zapisat'

Pri etom uravnenie sostoyaniya ispol'zuetsya v vide

gde v vyrazheniyah (14)-(18)  - udel'naya teploemkost' smesi;  - koncentraciya tyazhelogo komponenta binarnoi smesi;  - udel'noe energovydelenie radioaktivnogo elementa;  - koncentraciya radioaktivnogo elementa v tyazhelom komponente smesi;  - koefficient diffuzii;  - perekrestni koefficient. Analogichno (9)-(10) poluchaem usloviya gidrostaticheskogo ravnovesiya smesi pri malosti termodiffuzii:

Primenyaya operator k uravneniyu (19), poluchim

Takim obrazom, raspredelenie temperatury i koncentracii v sostoyanii gidrostaticheskogo ravnovesiya dolzhny byt' funkciyami tol'ko vertikal'noi koordinaty. Kraevye usloviya, sovmestimye s usloviyami (19)-(21) vyberem v vide

Usloviya v (22) na vertikal'nuyu komponentu skorosti oznachayut, chto granicy ne pronicaemye dlya zhidkosti i tak nazyvaemye «skol'zkie» (poslednee prinyato iz soobrazhenii udobstv posleduyushih vychislenii). Reshenie zadachi (21)-(22) imeet vid

Podstavlyaya (23) v (20), poluchim

Dlya harakternyh znachenii parametrov v mantii vyrazhenie (24) prinimaet vid

Teper' rassmotrim otklik sistemy na proizvol'nye malye izmeneniya sostoyaniya (19)-(21) i (23)-(24). Temperaturu, davlenie i koncentraciyu mozhno predstavit' v vide summy gidrostaticheski ravnovesnyh znachenii i malyh vozmushenii. Eti malye vozmusheniya takzhe opisyvayutsya uravneniyami konvekcii (14)-(17). Prezhde chem vypisat' sistemu uravnenii dlya vozmushenii, proizvedem ochen' vazhnoe preobrazovanie, pereidem k bezrazmernym peremennym (neobhodimo pomnit', chto operatory i razmerny!). V kachestve edinicy dliny vybiraem moshnost' sloya , edinicu vremeni ; skorosti ; temperatury , ; koncentracii , ; davleniya .

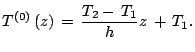
Togda kraevaya zadacha dlya vozmushenii v lineinom otnositel'no malyh vozmushenii priblizhenii mozhet byt' privedena k vidu

gde  - chislo Prandtlya;  - chislo Releya;
 - ego diffuzionnyi analog; ; . Levye chasti uravnenii (25)-(28) v otlichie ot ishodnyh
(14)-(17) ne soderzhat nelineinyh otnositel'no vozmushenii chlenov, poskol'ku voshli tol'ko gradienty gidrostaticheski ravnovesnyh raspredelenii temperatury i koncentracii. Togda vhodyashie v (25)-(28) funkcii vida mozhno predstavit' v vide:
. Vhodyashaya v pokazatel' eksponenty velichina nosit nazvanie dekrement zatuhaniya. Eto mozhet byt', voobshe govorya, kompleksnaya velichina. Narastanie ili zatuhanie vozmushenii opredelyaetsya veshestvennoi chast'yu , pri nashih oboznacheniyah dlya dannoe vozmushenie so vremenem zatuhaet. Esli eto vypolnyaetsya dlya vseh vozmozhnyh vozmushenii, to v sootvetstvii s opredeleniem ustoichivosti sistemy (12) analiziruemoe sostoyanie ustoichivo. Naprotiv, esli naidetsya vozmushenie, dlya dekrementa zatuhaniya kotorogo vypolnyaetsya , to amplituda takogo vozmusheniya bystro rastet i sostoyanie sistemy ne ustoichivo. Nizhe dlya oboznacheniya prostranstvennyh amplitud vozmushenii skorosti, temperatury i koncentracii my sohranim te zhe oboznacheniya , chto i v (25)-(28).

S tem chtoby izbavit'sya ot chlena s gradientom davleniya v (25) (dlya vozmusheniya davleniya ves'ma slozhno sformulirovat' granichnye usloviya), ispol'zuetsya standartnyi priem. Voz'mem 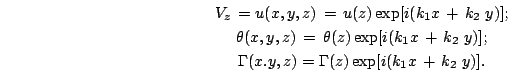ot obeih chastei uravneniya i sproektiruem na os' . Pri etom budem uchityvat', chto ni koefficienty v uravneniyah (25)-(28), ni granichnye usloviya ne zavisyat ot gorizontal'nyh koordinat. Poetomu vyrazheniya dlya prostranstvennyh amplitud mozhno vybrat' v vide

Togda uravnenie (25) privoditsya k vidu

gde verhnii indeks v skobkah oznachaet poryadok proizvodnoi po , a . Granichnye usloviya (28) pozvolyayut vybrat' zavisimost' amplitud ot vertikal'noi koordinaty v vide:

Podstavlyaya (30) v (25)-(27) s uchetom(29), poluchim

Iz uslovii sushestvovaniya netrivial'nogo resheniya sistemy odnorodnyh uravnenii (30) poluchaem

Predstaviv dekrement zatuhaniya v vide: 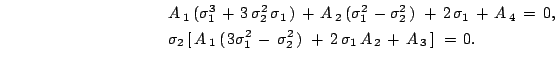i razdelyaya deistvitel'nuyu i mnimuyu chasti, poluchim

Takim obrazom, v sisteme vozmozhny kak monotonnye, strogo ubyvayushie libo vozrastayushie, tak i kolebatel'nye vozmusheniya.

Osobyi interes predstavlyaet sostoyanie neitral'noi ustoichivosti, t. e. , pri . Eto granica mezhdu ustoichivym i neustoichivym sostoyaniem. Kak sleduet iz (33), ono dostigaetsya pri 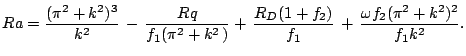, otkuda

Dlya harakternyh uslovii v mantii parametr 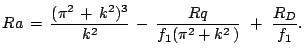ves'ma mal i (34) mozhno ostavit' v vide

Iz (35) vidno, chto ustoichivost' sistemy razlichna dlya vozmushenii razlichnoi dliny volny, . Kriticheskim nazyvayut minimal'noe znachenie funkcii . Pervyi chlen v etom vyrazhenii opisyvaet kriticheskoe znachenie chisla Releya v klassicheskoi zadache Releya-Benara. Tretii chlen v (35) poluchen v rabote [8] i otrazhaet uvelichenie konvektivnoi ustoichivosti sistemy, esli soderzhanie bolee plotnogo komponenta k verhnei granice uvelichivaetsya, ostavayas' maloi komponentoi smesi.

Principial'noe znachenie imeet vklad vtorogo chlena, otrazhayushego deistvie vnutrennih istochnikov tepla ( 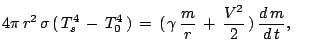). Ih nalichie privodit k umen'sheniyu plotnosti etogo komponenta smesi dazhe v tom sluchae, kogda istochniki tepla svyazany s bolee plotnym komponentom smesi. Otsyuda sleduet paradoks ustoichivosti, vpervye opisannyi v [9, 10]. On sostoit v tom, chto pri dostatochnoi moshnosti vnutrennih istochnikov tepla, koncentraciya kotoryh opredelyaetsya soderzhaniem bolee plotnogo komponenta smesi, imeetsya oblast' znachenii parametrov, kogda sistema ostaetsya v ustoichivom gidrostaticheskom sostoyanii pri uvelichenii koncentracii tyazhelogo komponenta po napravleniyu k verhnei holodnoi granice ploskogo sloya.

Chislennoe modelirovanie razvitoi konvekcii pokazalo, chto sistema stremitsya vynesti vnutrennie istochniki tepla, vhodyashie v odin iz komponentov smesi k verhnei holodnoi granice sloya [11].

---

<< 2. Uravneniya konvekcii | Oglavlenie | 4. Modelirovanie razvitoi konvekcii >>

Publikacii s klyuchevymi slovami: geofizika - stroenie Zemli - konvekciya Publikacii so slovami: geofizika - stroenie Zemli - konvekciya

Sm. takzhe: Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 6, 2020 g. Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 5, 2020 g. Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 4, 2020 g. Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 3, 2020 g. Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 2, 2020 g. Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 1, 2020 g. Annotacii osnovnyh statei zhurnala «Zemlya i Vselennaya» № 6, 2019 g. Vse publikacii na tu zhe temu >>