Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu

II. Protoplanetnye diski

A. Okruzhenie formiruyushihsya zvezd

Zvezdy i segodnya obrazuyutsya v Galaktike iz gaza, sosredotochennogo v nebol'shih i plotnyh yadrah molekulyarnyh oblakov. Molekulyarnye oblaka nablyudayutsya v odnoi ili neskol'kih molekulyarnyh liniyah (naprimer, v liniyah SO, 13SO i NH3), kazhdaya iz kotoryh mozhet byt' ispol'zovana kak dlya issledovaniya oblastei s razlichnoi plotnost'yu, tak i dlya polucheniya informacii o dvizhenii gaza (takogo, kak vrashenie, szhatie i t.p.). Nablyudeniya plotnyh, malen'kih po razmeram yader molekulyarnyh oblakov (s razmerami poryadka 0.1 pk), kotorye yavlyayutsya neposredstvennymi predshestvennikami formiruyushihsya zvezd, pokazyvayut gradienty skorosti, ravnye po poryadku velichiny 1 km/s na 1 pk. Dazhe esli ves' etot gradient pripisat' vrasheniyu, parametr

$$\beta\equiv\frac{E_{\mathrm{rot}}}{|E_{\mathrm{grav}}|} $$ (9)

okazyvaetsya malen'kim: chasto po poryadku velichiny on raven 0.01. Sledovatel'no, vrashenie ne yavlyaetsya osobenno vazhnym na rannih stadiyah kollapsa. S drugoi storony, uglovoi moment yadra molekulyarnogo oblaka okazyvaetsya bol'shim, po poryadku velichiny ravnym Jcore ~ 1054 g sm2/sek. Etot uglovoi moment gorazdo bol'she uglovogo momenta Solnechnoi sistemy, ne govorya uzh pro Solnce – nesootvetstvie, kotoroe nazvano "problemoi uglovogo momenta pri formirovanii zvezd". Polnoe reshenie etoi problemy zaklyuchaetsya v vozmozhnosti formirovaniya dvoinoi zvezdnoi sistemy, potere uglovogo momenta pri istechenii veshestva i formirovanii diska. Dlya nashih celei dostatochno otmetit', chto harakternyi uglovoi moment gaza v yadre molekulyarnogo oblaka sootvetstvuet harakternomu uglovomu momentu gaza na keplerovskoi orbite vokrug zvezdy solnechnoi massy s orbital'nym rasstoyaniem 10–100 a.e.

Podvedya chertu, otmetim, chto nablyudaemye svoistva yader molekulyarnyh oblakov sovmestimy s formirovaniem bol'shih diskov – razmerom s Solnechnuyu sistemu i bol'she – vokrug nedavno sformirovavshihsya zvezd. Srazu posle svoego formirovaniya eti diski mogut byt' ves'ma massivny.

Risunok 7. Shematicheskaya illyustraciya raspredeleniya energii v spektre molodoi zvezdy, okruzhennoi diskom. Sushestvovanie diska vyvoditsya iz infrakrasnogo izbytka v spektre (otnositel'no ozhidaemyh velichin, vychislennyh iz znaniya temperatury fotosfery molodoi zvezdy) na dlinah voln poryadka 1 mm. Chasto nablyudaetsya takzhe ul'trafioletovyi izbytok, kotoryi yavlyaetsya priznakom akkrecii gaza na poverhnost' zvezdy, privodyashei k poyavleniyu goryachih pyaten.

Molodye zvezdnye ob'ekty klassificiruyutsya po forme ih spektrov v infrakrasnom diapazone. Kak pokazyvaet Risunok 7, molodye zvezdnye ob'ekty chasto demonstriruyut:

  1. Infrakrasnyi izbytok v spektre kak priznak nalichiya goryachei pyli v okolozvezdnom diske.
  2. Ul'trafioletovyi izbytok v spektre, kotoryi govorit o nalichii na poverhnosti zvezdy oblastei s vysokoi temperaturoi (goryachih pyatnah), gde akkumuliruetsya gaz iz diska.
Chtoby opredelit' velichinu infrakrasnogo izbytka v spektre, polezno vvesti meru naklona spektra mezhdu blizhnim IK–diapazonom (2.2 mkm) i srednim IK–diapazonom (10 mkm):

$$\alpha_{\mathrm{IR}}=\frac{\Delta\log(\lambda F_\lambda)}{\Delta\log\lambda}$$ (10)

My budem klassificirovat' molodye zvezdnye ob'ekty kak:

Eta shema klassifikacii ob'ektov, osnovannaya na nablyudeniyah, poluchila i teoreticheskuyu interpretaciyu, otchasti kak evolyucionnaya posledovatel'nost' (Adams, Lada & Shu, 1987). V chastnosti, rannie ob'ekty nulevogo klassa, teryaya svoi diski, stanovyatsya ob'ektami vtorogo klassa i, v konechnom schete, stanovyatsya ob'ektami tret'ego klassa. Ugol naklona sistemy k luchu zreniya tozhe igraet vazhnuyu rol': v zavisimosti ot nego ob'ekt mozhet vyglyadet' kak ob'ekt pervogo ili vtorogo klassa.

B. Passivnye okolozvezdnye diski

Sushestvuet vazhnoe fizicheskoe razlichie mezhdu passivnymi okolozvezdnymi diskami, kotorye tol'ko pereizluchayut svet zvezdy, i aktivnymi diskami, kotorye pererabatyvayut potencial'nuyu gravitacionnuyu energiyu gaza v energiyu gazovyh potokov. Dlya diska s prirostom massy $\dot M$, vrashayushimsya vokrug zvezdy so svetimost'yu L i radiusom R, ravnym dvum solnechnym radiusam, kriticheskaya skorost' akkrecii, nizhe kotoroi energiei akkrecii mozhno prenebrech', mozhet byt' ocenena kak:

$$\frac{1}{4}L_\odot=\frac{GM_*\dot M}{2R_*}\,,$$ (11)

gde uchityvaetsya, kak budet pokazano nizhe, chto disk perehvatyvaet primerno chetvert' svetovogo potoka ot zvezdy. Chislenno

$$\dot M \approx 3\times10^{-8}M_\odot/\textrm{god}\,. $$ (12)

Skorost' akkrecii, izmerennaya u klassicheskih zvezd tipa T Tel'ca, menyaetsya po poryadku velichiny ot znacheniya vyshe kriticheskoi do znachenii na dva poryadka nizhe. Takim obrazom, nel'zya schitat', chto protoplanetnye diski yavlyayutsya ili vsegda passivnymi, ili vsegda aktivnymi. Skoree, teplovaya struktura diskov na rannih stadiyah bol'she napominaet strukturu aktivnogo diska s vydeleniem tepla iz–za akkrecii, a na pozdnih stadiyah preobladaet prostoe pereizluchenie sveta zvezdy.

1. Vertikal'naya struktura

Vertikal'naya struktura geometricheski tonkogo diska (ne vazhno, aktivnogo ili passivnogo) opredelyaetsya rassmotreniem vertikal'nogo gidrostaticheskogo ravnovesiya (Risunok 8):

$$\frac{dP}{dz}=-\rho g_z\,,$$ (13)

gde ρ – plotnost' gaza. Ignoriruya gravitacionnoe vliyanie diska (obychno eto opravdanno), poluchim, chto vertikal'nyi komponent sily prityazheniya, deistvuyushii na cilindricheskii ob'em gaza s radiusom r i vysotoi nad usrednennoi ploskost'yu diska z, raven:

$$g_z=\frac{GM_*}{d^2}\sin\theta=\frac{GM_*}{d^3}z\,.$$ (14)

Dlya tonkogo diska z<<r, i

$$g_z\simeq \Omega^2z\,, $$ (15)

gde Ω=(GM*/r3)1/2 – keplerovskaya uglovaya skorost'. Esli my dlya prostoty predpolozhim, chto disk yavlyaetsya vertikal'no izotermicheskim (chto yavlyaetsya horoshim priblizheniem dlya passivnogo diska i ne ochen' horoshim dlya aktivnogo diska), togda uravnenie sostoyaniya budet: R=ρss2, gde ss – skorost' zvuka. Uravnenie gidrostaticheskogo ravnovesiya (formula 13) togda mozhet byt' perepisana kak:

$$c_s^2\frac{d\rho}{dz}=-\Omega^2\rho z\,.$$ (16)

Eto uravnenie imeet reshenie:

$$\rho=\rho(z=0)e^{-z^2/h^2}\,,$$ (17)

gde h – vertikal'nyi masshtab umen'sheniya plotnosti,

$$h=\sqrt{2\,}\frac{c_s}{\Omega}\,.$$ (18)

Sravnivaya tolshinu diska s ego radiusom, poluchim:

$$\frac{h}{r} \approx \frac{c_s}{v_\phi}\,, $$ (19)

gde vφ – lokal'naya orbital'naya skorost'. My vidim, chto tolshina diska h/r proporcional'na chislu Maha gazovogo potoka.

Risunok 8. Grafik dlya vychisleniya vertikal'nogo gidrostaticheskogo ravnovesiya v okolozvezdnom diske.
Risunok 9. Grafik dlya vychisleniya temperaturnogo profilya ploskogo passivnogo diska. My rassmatrivaem poverhnost' edinichnoi ploshadi v ploskosti diska na rasstoyanii r ot zvezdy radiusa R*. Os' sfericheskih polyarnyh koordinat – liniya mezhdu poverhnost'yu i centrom zvezdy, prichem ugol φ=0 v napravlenii na polyus zvezdy.

Forma diska zavisit ot otnosheniya h(r)/r. Esli my parametrizuem izmeneniya radial'noi skorosti zvuka kak

$$c_s \propto r^{-\beta}\,,$$ (20)

togda zavisimost' tolshiny diska ot radiusa budet

$$\frac{h}{r}\propto r^{-\beta+1/2}\,.$$ (21)

Disk budet tolstym (t.e. h/r budet uvelichivat'sya s uvelicheniem radiusa, delaya disk pohozhim na shar), esli β < 1/2. Dlya etogo trebuetsya, chtoby temperaturnyi profil' T(r)~r-1 ili bolee pologii. Kak my korotko pokazhem, tolstye diski – normal'noe yavlenie, osobenno blizko ot zvezdy.

2. Radial'nyi temperaturnyi profil'

Fizika vychislenii radial'nogo temperaturnogo profilya passivnogo diska byla opisana v rabotah Adams & Shu (1986), Kenyon & Hartmann (1987) i Chiang & Goldreich (1997). My nachnem rassmotrenie s prosteishei modeli tonkogo ploskogo diska, v ekvatorial'noi ploskosti kotorogo pogloshaetsya vse popavshee na nego zvezdnoe izluchenie i pereizluchaetsya po zakonu chernogo tela v sootvetstvii s lokal'noi temperaturoi. Nagrevom zvezdy diskom prenebregaem.

Rassmotrim poverhnost' v ploskosti diska na rasstoyanii r ot zvezdy radiusa R. Zvezda predstavlena sferoi s postoyannoi yarkost'yu I. Vvedya sfericheskie polyarnye koordinaty, kak eto pokazano na Risunke 9, my poluchim, chto potok zvezdnogo sveta, prohodyashii cherez etu poverhnost', raven:

$$F=\int I_*\sin\theta\cos\phi d\Omega\,.$$ (22)

My uchityvaem tol'ko potok, prihodyashii ot verhnei poloviny zvezdy, i izluchenie tol'ko verhnei poloviny diska. Togda predely integrirovaniya budut:

$$-\pi/2 < \phi \leq \pi/2\,,$$
$$0 < \theta < \sin^{-1} \left(\frac{R_*}{r}\right)\,.$$		 (23)

Podstavlyaya dΩ = sin θ dθ dφ, poluchim integral dlya izlucheniya:

$$F=\int_{-\pi/2}^{\pi/2} \cos\phi d\phi \int_0^{\sin^{-1}(R_*/r)}\sin^2\theta d\theta\,,$$ (24)

kotoryi raven

$$F=I_* \left[ \sin^{-1}\left(\frac{R_*}{r}\right) -\left(\frac{R_*}{r}\right) \sqrt{1-\left(\frac{R_*}{r}\right)^2\,} \right]\,. $$ (25)

Dlya zvezdy s effektivnoi temperaturoi T yarkost' I*=(1/π)σT*4, zdes' σ – postoyannaya Stefana-Bol'cmana. Priravnivaya F k izlucheniyu odnoi storony diska σTdiska4, my poluchim radial'nyi temperaturnyi profil':
$$\left(\frac{T_{\mathrm{disk}}}{T_*}\right) = \frac{1}{\pi} \left[\sin^{-1}\left(\frac{R_*}{r}\right) -\left(\frac{R_*}{r}\right) \sqrt{1-\left({R_*}{r}\right)^2\,} \right]\,.$$ (26)

Integriruya po radiusu, my poluchim polnuyu yarkost' diska:

$$F=2\times\int_{R_*}^\infty 2\pi r\sigma T_{\mathrm{disk}}^4 dr = \frac{1}{4} F_*\,.$$ (27)

My prishli k vyvodu, chto ploskii passivnyi disk, ohvatyvayushii zvezdnyi ekvator, perehvatyvaet chetvert' zvezdnogo izlucheniya. Otnoshenie nablyudaemoi bolometricheskoi yarkosti takogo diska k yarkosti zvezdy budet menyat'sya v zavisimosti ot ugla naklona sistemy k luchu zreniya, no v lyubom sluchae yarkost' diska vsegda men'she yarkosti zvezdy. Forma temperaturnogo profilya, poluchennaya iz vyrazheniya (26), ne slishkom ochevidna. Razlagaya pravuyu chast' uravneniya po Teiloru (i schitaya R << r, t.e. rech' idet o diske dostatochno daleko ot zvezdnoi poverhnosti), poluchim:

$$T_{\mathrm{disk}} \propto r^{-3/4}\,, $$ (28)

kak predel'nyi temperaturnyi profil' tonkogo, ploskogo, passivnogo diska. Dlya gaza s postoyannoi molekulyarnoi massoi mu eto privodit k profilyu skorosti zvuka

$$c_s \propto r^{-3/8}\,. $$ (29)

Schitaya disk vertikal'no izotermichnym, my poluchim i vyrazhenie dlya tolshiny diska:

$$\frac{h}{r} \propto r^{1/8}\,, $$ (30)

i predskazyvaem, chto disk dolzhen nemnogo rasshiryat'sya s rostom rasstoyaniya do zvezdy. Esli eto deistvitel'no proishodit, to vneshnie chasti diska perehvatyvayut bol'shuyu dolyu zvezdnogo sveta i nagrevayutsya do bolee vysokih temperatur. Sledovatel'no, temperaturnyi profil' Tdisk ∝ r-3/4 – samyi krutoi profil', kotoryi mozhno poluchit' dlya passivnogo diska.

Risunok 10. Zdes' shematicheski pokazan spektr diska. Na korotkih volnah my vidim eksponencial'noe spadanie, sootvetstvuyushee vysokotemperaturnomu kol'cu diska (obychno na vnutrennem krayu). Na dlinnyh volnah raspolozhen "hvost" Releya–Dzhinsa, otrazhayushii izluchenie holodnogo materiala vo vneshnei chasti diska. Na srednih volnah nahoditsya ploskaya chast' spektra, tak kak polnyi spektr otrazhaet izluchenie protyazhennogo chernogo tela.

3. Raspredelenie energii v spektre

Predpolozhim, chto kazhdoe kol'co v diske izluchaet kak absolyutno chernoe telo s lokal'noi temperaturoi Tdisk(r). Esli disk prostiraetsya ot rin do rout, spektr diska yavlyaetsya summoi spektrov takih tel:

$$F_\lambda \propto \int_{r_{in}}^{r_{out}} 2\pi r B_\lambda[E(r)] dr\,,$$ (31)

gde Bλ – funkciya Planka:

$$B_\lambda(T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{hc/\lambda kT}-1}\,, $$ (32)

Povedenie spektra, vyrazhennogo vyrazheniem (31), legko predstavit'. Na dlinnyh volnah (λ >> hc/kT(rout)) my vozvrashaemsya k formule Releya-Dzhinsa:

$$\lambda F_\lambda \propto \lambda^{-3}\,, $$ (33)

togda kak dlya korotkih voln (λ << hc/kT(rin)) nablyudaetsya eksponencial'noe spadanie energii v spektre, chto sootvetstvuet samomu goryachemu krayu diska:

$$\lambda F_\lambda \propto \lambda^{-4} e^{-hc/\lambda kT(r_{in})}\,. $$ (34)

Dlya promezhutochnyh dlin voln

$$\frac{hc}{kT(r_{in})} \ll \lambda \ll \frac{hc}{kT(t_{out})} $$ (35)

formiruetsya spektr, kotoryi mozhet byt' naiden podstanovkoi

$$x\equiv \frac{hc}{\lambda kT(r_{in})} \left(\frac{r}{r_{in}}\right)^{3/4} $$ (36)

v uravnenie (31). My imeem togda, priblizitel'no,

$$F_\lambda \propto \lambda^{-7/3} \int_0^\infty \frac{x^{5/3}dx}{e^x-1} \propto \lambda^{-7/3} $$ (37)

i

$$\lambda F_\lambda \propto \lambda^{-4/3}\,. $$ (38)

Obshii vid spektra, shematicheski pokazannyi na Risunke 10, yavlyaetsya spektrom "protyazhennogo" chernogo tela (Lynden-Bell, 1969).

Raspredelenie energii v spektre, predskazannoe etoi prostoi model'yu, demonstriruet infrakrasnyi izbytok, no s ponizheniem v oblasti srednih infrakrasnyh voln. Eto slishkom kruto, chtoby sootvetstvovat' nablyudeniyam dazhe istochnikov vtorogo klassa.

4. Eskiz bolee polnyh modelei

Dlya vychisleniya detal'nogo vida spektra passivnogo ploskogo diska neobhodimo uchityvat' eshe dva obstoyatel'stva. Pervoe, kak bylo pokazano vyshe, zaklyuchaetsya v tom, chto disk rasshiryaetsya s rostom r, i, kak sledstvie, pogloshaet i pererabatyvaet bol'shuyu dolyu zvezdnogo sveta. Dlya bol'shih r Kenyon & Hartmann (1987) nashli, chto rasshiryayushiesya po mere udaleniya ot zvezdy diskovye modeli privodyat k temperaturnomu profilyu

$$T_{\mathrm{disk}} \propto r^{-1/2}\,, $$ (39)

kotoryi bolee ploskii, chem profil', poluchennyi vyshe. Vtoroe obstoyatel'stvo zaklyuchaetsya v tom, chto predpolozhenie o chernotel'nom haraktere izlucheniya diska okazyvaetsya slishkom prostym. Fakticheski pyl' v poverhnostnom sloe diska izluchaet kak bolee nagretoe telo, potomu chto ona gorazdo effektivnee pogloshaet zvezdnyi svet na bolee korotkih volnah, chem izluchaet v srednem infrakrasnom diapazone (Shlosman & Begelman, 1989). Chasticy pyli razmerom a effektivno pogloshayut svet s dlinoi volny λ < 2πa, no ploho pogloshayut i izluchayut volny s dlinoi volny λ > 2πa. V rezul'tate disk pogloshaet zvezdnyi svet vblizi svoei poverhnosti (gde opticheskaya glubina poryadka edinicy), no v etoi oblasti opticheskaya glubina na izluchenie v dal'nem infrakrasnom diapazone okazyvaetsya mnogo men'she edinicy. Izluchenie, prihodyashee iz poverhnostnogo sloya diska, okazyvaetsya bolee goryachim, chem eto bylo predskazano v modeli "protyazhennogo chernogo tela".

Chiang & Goldreich (1997) pokazali, chto otnositel'no prostaya diskovaya model', vklyuchayushaya v sebya:

  1. Goryachii poverhnostnyi sloi pyli, kotoryi neposredstvenno pereizluchaet polovinu zvezdnogo sveta, i
  2. Bolee holodnuyu vnutrennyuyu chast' diska, kotoraya pererabatyvaet vtoruyu polovinu zvezdnogo sveta v teplovoe izluchenie,
s uchetom rasshireniya diska po krayam, mozhet prekrasno vosproizvodit' bol'shinstvo nablyudaemyh spektrov. Obzor nedavnih rabot po modelirovaniyu diskov sdelan Dullemond et al. (2007).

Privedennye vykladki v principe dostatochny dlya togo, chtoby ponyat' strukturu i formu spektra istochnikov vtorogo klassa. Odnako dlya istochnikov pervogo klassa vozmozhno nalichie obolochki (sostoyashei iz gaza i pyli, prodolzhayushih padat' na protozvezdu s protoplanetnym diskom), chto takzhe nuzhdaetsya v rassmotrenii. Napravlyaem chitatelya k Eisner et al. (2005) dlya izucheniya odnogo iz primerov modelirovaniya takih sistem.

V. Aktivnye akkrecionnye diski

Radial'nyi balans sil v passivnom diske vklyuchaet v sebya vklad gravitacii, centrobezhnoi sily i radial'nogo gradienta davleniya. Zapishem sootvetstvuyushee uravnenie:

$$\frac{v_\phi^2}{r} = \frac{GM_*}{r^2} + \frac{1}{\rho}\frac{dP}{dr}\,,$$ (40)

gde vφ – radial'naya skorost' gaza, R – davlenie.

Chtoby ocenit' velichinu gradienta davleniya, zametim, chto

$$\frac{1}{\rho}\frac{dP}{dr} \sim -\frac{1}{\rho}\frac{P}{r} \sim -\frac{1}{\rho}\frac{\rho c_s^2}{r} \sim -\frac{GM_*}{r^2} \left(\frac{h}{r}\right)^2\,,$$ (41)

gde na poslednem shage my sdelali podstanovku h ~ cs/Ω. Esli vK – keplerovskaya skorost' na rasstoyanii r ot zvezdy, to my imeem:

$$v_\phi^2 = v_{K}^2 \left[ 1-{\cal O}\left(\frac{h}{r}\right)^2 \right]\,, $$ (42)

t.e. v sluchae tonkogo (h << r)*** diska gradientom gazovogo davleniya mozhno prenebrech' po sravneniyu s krivoi vrasheniya gaza.

***[Odnako eto ne oznachaet, chto gradient davleniya voobshe ne vazhen. Kak my uvidim dal'she, nebol'shaya raznica mezhdu v i vk priobretaet ogromnoe znachenie dlya dinamiki nebol'shih kameshkov v diske.]

S ochen' nebol'shoi pogreshnost'yu mozhno skazat', chto uglovoi moment gaza v diske raven uglovomu momentu dvizheniya po sootvetstvuyushei keplerovskoi orbite:

$$\ell = r^2\Omega = \sqrt{GM_*r\,}\,,$$ (43)

kotoryi yavlyaetsya vozrastayushei funkciei r. Padaya na zvezdu, gaz v diske dolzhen utratit' uglovoi moment:

  1. Cherez pereraspredelenie uglovogo momenta v diske (obychno opisyvaemoe kak "vyazkost'", hotya eto ne sovsem tochnyi termin),
  2. Cherez utratu uglovogo momenta iz sistemy zvezda+disk, naprimer, putem istecheniya namagnichennogo diskovogo vetra.
Modeli vtorogo klassa – est' horosho izvestnyi primer, v kotorom reshenie dlya diskovogo vetra bylo polucheno Blandford & Payne (1982) – shiroko ne obsuzhdayutsya (vozmozhno, nezasluzhenno) – v chastnosti, potomu, chto v neskol'kih belyh karlikah, okruzhennyh akkrecionnymi diskami, nablyudayutsya neblagopriyatnye (disfavor) modeli vetra, hotya tam net ogranichenii, sushestvuyushih dlya protoplanetnyh diskov. Zdes' my poluchim uravneniya dlya vremeni evolyucii poverhnostnoi plotnosti tonkogo vyazkogo diska (Lynden–Bell & Pringle, 1974; Shakura & Sunyaev, 1973). Horoshii obzor fundamental'nyh teorii diskovoi akkrecii mozhno naiti u Pringle (1981) i Frank, King & Raine (2002).

1. Diffuzionnoe uravnenie evolyucii

Pust' disk imeet poverhnostnuyu plotnost' S(r,t) i radial'nuyu skorost' vr(r,t), prichem vr < 0 sootvetstvuet priblizheniyu k zvezde. Potencial ustanovlen tak, chto uglovaya skorost' zavisit tol'ko ot rasstoyaniya do zvezdy: Ω = &Omega(r). V cilindricheskih koordinatah uravnenie nepreryvnosti dlya osesimmetrichnogo potoka (sm., naprimer, Pringle (1981)):

$$r\frac{\partial\Sigma}{\partial t} = \frac{\partial}{\partial r}(r\Sigma v_r)=0\,.$$ (44)

Analogichno, sohranenie uglovogo momenta daet:

$$r\frac{\partial\Sigma r^2\Omega}{\partial t} = \frac{\partial}{\partial r}(r\Sigma v_r \cdot r^2\Omega) = \frac{1}{2\pi} \frac{\partial G}{\partial r}\,,$$ (45)

gde chlen v pravoi chasti uravneniya sootvetstvuet vrashatel'nomu momentu, deistvuyushemu na potok vsledstvie sil vyazkosti. Kak izvestno iz gidrodinamiki (Pringle, 1981), G daetsya v terminah kinematicheskoi vyazkosti ν soglasno vyrazheniyu:

$$G=2\pi r \nu\Sigma r \frac{d\Omega}{dr} \cdot r\,,$$ (46)

gde pravaya storona uravneniya est' rezul'tat proizvedeniya dliny okruzhnosti, sily vyazkosti na edinicu dliny i dlinu plecha r. Esli my zamenyaem G, isklyuchaem iz uravneniya vr s pomosh'yu uravnenii (44) i (45) i ogranichivaemsya keplerovskim potencialom s Ω ~ r-3/2, my poluchim evolyucionnoe uravnenie dlya poverhnostnoi plotnosti tonkogo akkrecionnogo diska v ego normal'noi forme:

$$\frac{\partial\Sigma}{\partial t} = \frac{3}{r} \frac{\partial}{\partial r} \left[ r^{1/2} \frac{\partial}{\partial r}(\nu\Sigma r^{1/2})\right]\,.$$ (47)

Eto chastnoe differencial'noe uravnenie dlya evolyucii poverhnostnoi plotnosti S imeet formu uravneniya diffuzii. Chtoby sdelat' eto yavnym, sovershim podstanovku:

$$X \equiv 2r^{1/2}\,,$$
$$f \equiv \frac{3}{2} \Sigma X\,.$$		 (48)

Dlya postoyannoi kinematicheskoi vyazkosti ν uravnenie (47) togda prinimaet tipichnuyu formu uravneniya diffuzii:

$$\frac{\partial f}{\partial t} = D \frac{\partial^2 f}{\partial X^2}$$ (49)

s koefficientom diffuzii

$$V = \frac{12\nu}{X^2}\,.$$ (50)

Harakternoe vremya diffuzii, poluchennoe iz uravneniya (49), ravno X2/D. Vozvrashayas' obratno k fizicheskim peremennym, my obnaruzhim, chto harakternoe vremya evolyucii diska na rasstoyanii r ot zvezdy s kinematicheskoi vyazkost'yu ν ravno:

$$\tau \simeq \frac{r^2}{\nu}\,. $$ (51)

Nablyudeniya evolyucii diska (naprimer, opredelenie harakternogo vremeni vekovogo umen'sheniya skorosti akkrecii) vmeste s ocenkami razmerov diska mogut pomoch' opredelit' effektivnuyu vyazkost' diska (Hartmann et al., 1998).

2. Resheniya

V obshem sluchae vyazkost' yavlyaetsya funkciei mestnyh uslovii v diske (takih, kak poverhnostnaya plotnost', rasstoyanie do zvezdy, temperatura, stepen' ionizacii i t.d.) Esli vyazkost' ν zavisit ot poverhnostnoi plotnosti S, togda uravnenie (47) stanovitsya nelineinym uravneniem, kotoroe ne imeet analiticheskih reshenii (krome neskol'kih osobyh sluchaev). Esli est' bolee slozhnaya zavisimost' ot mestnyh uslovii, togda uravnenie evolyucii poverhnostnoi plotnosti dolzhno byt' resheno odnovremenno s uravneniem evolyucii central'noi temperatury (Pringle, Verbunt & Wade, 1986). Odnako analiticheskoe reshenie vozmozhno, esli u mozhet byt' zapisano kak stepennaya funkciya r (Lynden–Bell & Pringle, 1974), i etogo dostatochno dlya illyustracii osnovnogo povedeniya resheniya uravneniya (47).

Snachala my opishem reshenie dlya funkcii Grina dlya sluchaya ν=const. Predpolozhim, chto v moment vremeni t=0 ves' gaz sosredotochen v tonkom kol'ce massoi m i radiusom r0:

$$\Sigma(r,t=0) = \frac{m}{2\pi r_0}\delta(r-r_0)\,. $$ (52)

Legko pokazat', chto ego reshenie:

$$\Sigma(x,\tau)=\frac{m}{2\pi r_0} \frac{1}{\tau} x^{-1/4} e^{-(1+x^2)/\tau} I_{1/4}\left(\frac{2x}{\tau}\right)\,, $$ (53)

gde my zapisali reshenie v bezrazmernyh peremennyh x=r/r0, τ=12νt/r02, I1/4 – modificirovannaya funkciya Besselya pervogo roda.

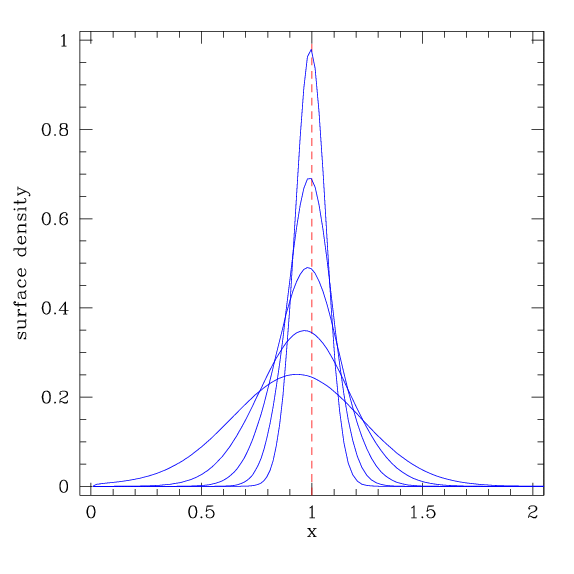
Esli Vy ne vodite blizkoe znakomstvo s funkciyami Besselya, reshenie dlya funkcii Grina ne pokazhetsya Vam osobenno yasnym i prozrachnym. Evolyuciya, podrazumevaemaya etim resheniem, predstavlena na Risunke 11. Naibolee vazhnye svoistva resheniya, pri t, stremyashemsya k beskonechnosti – eto:

  1. Potok massy k r = 0, i
  2. Uglovoi moment, unosimyi nebol'shoi dolei massy, techet k r = beskonechnosti.
Risunok 11. Chislennoe reshenie uravneniya evolyucii diska dlya sluchaya ν=const, vycherchennoe dlya znachenii bezrazmernogo vremeni τ, ravnogo 0.01, 0.02, 0.04, 0.08 i 0.16. Nachal'noe sostoyanie predstavlyaet soboi uzkoe kol'co s massoi m pri x = 1. Dlya x = 0.01 bylo primeneno granichnoe uslovie: ravnyi nulyu uglovoi moment. Zametim, chto iz-za etogo granichnogo usloviya reshenie uravneniya na bolee pozdnih vremenah nemnogo otlichaetsya ot analiticheskogo resheniya, dannogo v tekste.

Eto razdelenie massy i uglovogo momenta – geneticheskaya osobennost' evolyucii vyazkogo diska, i ona yavno vazhna dlya resheniya problemy uglovogo momenta pri formirovanii zvezd.

Bol'shuyu prakticheskuyu pol'zu prineslo samopodobnoe reshenie, takzhe poluchennoe Lynden–Bell & Pringle (1974). Rassmotrim disk, v kotorom vyazkost' menyaetsya kak stepennaya funkciya rasstoyaniya do zvezdy:

$$\nu \propto r^\gamma\,.$$ (54)

Predpolozhim, chto disk v moment vremeni, ravnyi nulyu, imeet profil' poverhnostnoi plotnosti, sootvetstvuyushii ustoichivomu, ustanovivshemusya resheniyu sostoyaniya (s etim zakonom izmeneniya vyazkosti) do r = r1 s eksponencial'nym snizheniem plotnosti dlya bol'shih r. Kak my kratko pokazhem nizhe, nachal'naya poverhnostnaya plotnost' v etom sluchae imeet formu:

$$\Sigma(t=0)=\frac{C}{3\pi\nu_1 \widetilde{r}\gamma} e^{-\widetilde{r}(2-\gamma)}\,, $$ (55)

gde S – konstanta, . Avtomodel'noe reshenie togda:

$$\Sigma(\widetilde{r},T)=\frac{C}{3\pi\nu_1\widetilde{r}\gamma} T^{-(5/2-\gamma)(2-\gamma)} e^{-\widetilde{r}(2-\gamma)/T}\,,$$ (56)

gde

$$T \equiv \frac{t}{t_s} + 1\,,$$
$$t_s \equiv \frac{1}{3(2-\gamma)^2} \frac{r_1^2}{\nu_1}\,.$$		 (57)

Eto reshenie pokazano na Risunke 12.

Risunok 12. Avtomodel'noe reshenie uravneniya evolyucii diska dlya sluchaya γ = 1, vycherchennoe dlya velichin bezrazmernogo vremeni T, ravnyh 1, 2, 4 i 8. Velichina poverhnostnoi plotnosti po osi y proizvol'na.

V techenie dolgogo vremeni massa diska umen'shaetsya, v to vremya kak harakternyi masshtab diska (iznachal'no ravnyi r1) uvelichivaetsya s sohraneniem uglovogo momenta. Eto reshenie ves'ma polezno kak dlya analiticheskogo izucheniya evolyucii diskov, tak i dlya sravneniya nablyudaemyh mass i razmerov diskov i skorosti akkrecii s teoriei (Hartmann et al., 1998).

Stacionarnoe reshenie dlya zavisimosti poverhnostnoi plotnosti diska ot radiusa mozhet byt' vyvedeno iz usloviya $\partial/\partial t = 0$ i integrirovaniya uravneniya (45) s usloviem sohraneniya uglovogo momenta:

$$\Sigma r^3\Omega v_r = \nu\Sigma r^3 \frac{d\Omega}{dr} + \textrm{const}\,. $$ (58)

Zametiv, chto skorost' akkrecii $\dot M=-2\pi r \Sigma v_r$, my imeem:

$$-\frac{\dot M}{2\pi} r^2\Omega = \nu\Sigma r^3 \frac{d\Omega}{dr} + \textrm{const}\,. $$ (59)

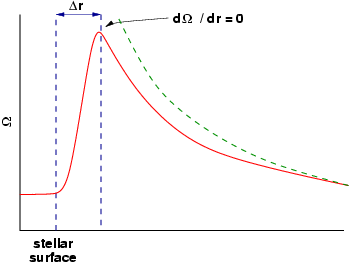
Dlya opredeleniya konstanty integrirovaniya otmetim, chto vrashatel'nyi moment diska ischezaet, esli dΩ/dr = 0. V etom sluchae konstanta mozhet byt' ocenena, ona budet proporcional'na lokal'nomu potoku uglovogo momenta:

$$\textrm{const} \propto \dot M r^2 \Omega\,. $$ (60)

Obychno on opredelyaetsya na vnutrennei granice diska. Osobenno prostoi primer – eto sluchai diska, kotoryi prostiraetsya ot ekvatora medlenno vrashayusheisya zvezdy. Etot sluchai proillyustrirovan na Risunke 13.

Risunok 13. Shematicheskii grafik zavisimosti uglovoi skorosti Ω(r) dlya medlenno vrashayusheisya zvezdy, okruzhennoi tonkim akkrecionnym diskom, rasprostranyayushimsya ot zvezdnogo ekvatora. Pri bol'shih radiusah v diske uglovaya skorost' menyaetsya po normal'nomu keplerovskomu zakonu, pokazannomu punktirnoi zelenoi liniei. Chtoby gladko pereiti na vrashenie ekvatora zvezdy, uglovaya skorost' dolzhna povernut' (nachat' umen'shat'sya) na malyh rasstoyaniyah ot zvezdy v perehodnoi zone, izvestnoi kak granichnyi sloi. Sushestvovanie granichnogo sloya predpolagaet, chto na nekotorom rasstoyanii ot zvezdy dΩ/dr = 0, i v etoi tochke vyazkoe napryazhenie ischezaet.

V zone perehoda mezhdu keplerovskim profilem uglovoi skorosti v diske i namnogo men'shei uglovoi skorost'yu na poverhnosti zvezdy dolzhen byt' maksimum v uglovoi skorosti gaza Ω na nekotorom radiuse r*+Δr. Elementarnye argumenty (Pringle, 1977) – kotorye, odnako, mogut byt' neprimenimy pri ochen' vysokih skorostyah akkrecii ob'ektov tipa FU Oriona (t.n. fuorov) (Popham et al., 1993), no verny vo vseh prochih sluchayah – govoryat o tom, chto Δr<<r, tak chto etot perehod proishodit v uzkom pogranichnom sloe vblizi poverhnosti zvezdy***.

***[Fizika samogo granichnogo sloya predstavlyaetsya ves'ma interesnym prilozheniem, tak kak granichnyi sloi – oblast' sil'nyh sdvigov, kotorye ustoichivy v protivopolozhnost' magnitovrashatel'noi neustoichivosti, kotoraya, kak my obsudim pozzhe, yavlyaetsya kriticheskoi dlya perenosa uglovogo momenta v disk. Pringle (1989), Armitage (2002) i Pessah, Chan & Psaltis (2006) izuchali rol' magnitnyh polei v perehodnom sloe.]

Konstanta iz uravneniya (59) togda mozhet byt' vychislena kak:

$$\textrm{const} \approx -\frac{\dot M}{2\pi} r_*^2 \sqrt{\frac{GM_*}{r_*^3}\,}\,,$$ (61)

i uravnenie (59) stanovitsya

$$\nu\Sigma = \frac{\dot M}{3\pi} \left(1-\sqrt{\frac{r_*}{r}\,}\right)\,. $$ (62)

Uchityvaya vyazkost', eto uravnenie opredelyaet stacionarnoe sostoyanie profilya poverhnostnoi plotnosti diska so skorost'yu akkrecii $\dot M$. Vdali ot granicy S(r) ~ ν-1.

Vnutrennie granichnye usloviya, kotorye privodyat k uravneniyu (62), opisany kak granichnoe uslovie nulevogo momenta. Kak uzhe bylo zamecheno, uslovie nulevogo uglovogo momenta fizicheski realizuetsya, kogda sushestvuet granichnyi sloi mezhdu zvezdoi i ee diskom. Etogo net, odnako, v sluchae klassicheskih zvezd tipa T Tel'ca. Nablyudatel'nye dannye (Bouvier et al., 2007) govoryat o tom, chto pri akkrecii na zvezdy tipa T Tel'ca zvezdnaya magnitosfera razrushaet vnutrennii akkrecionnyi disk, privodya k magnitosfernomu tipu akkrecii, pri kotorom gaz "prikleevaetsya" k liniyam zvezdnogo magnitnogo polya i ballisticheski padaet na poverhnost' zvezdy (Königl, 1991). Magnitnoe sceplenie mezhdu zvezdoi i ee diskom vvodit popravku v obmen uglovym momentom, izmenyaet stacionarnyi profil' poverhnostnoi plotnosti vblizi vnutrennego radiusa usecheniya i mozhet zastavit' zvezdu vrashat'sya medlennee, chem v inom sluchae (Armitage & Clarke, 1996; Collier Cameron & Campbell, 1993). Reguliruet li takoi "zahvat diska" real'noe vrashenie molodyh zvezd, ostaetsya predmetom diskussii (Herbst & Mundt, 2005; Matt & Pudritz, 2005; Rebull et al., 2006).

3. Temperaturnyi profil'

Pol'zuyas' metodom Frank, King & Raine (2002), my poluchim radial'nuyu zavisimost' effektivnoi temperatury aktivnogo akkrecionnogo diska, rassmatrivaya chistyi vrashatel'nyi moment kol'ca shirinoi Δr. Etot moment – $(\partial G/\partial r)\Delta r$ :

$$\Omega \frac{\partial G}{\partial r} \Delta r \equiv \left[ \frac{\partial}{\partial r}(G\Omega) - G\Omega^\prime \right] \Delta r\,. $$ (63)

Zapisav eto vyrazhenie, my zametim, chto, esli rassmatrivat' ves' disk (integriruya po r), to pervyi chlen vyrazheniya v pravoi chasti uravneniya opredelen isklyuchitel'no granichnymi velichinami G Sigma. Sledovatel'no, my otozhdestvlyaem etot chlen s perenosom energii, svyazannym s momentom vyazkosti, tekushim skvoz' kol'co. S drugoi storony, vtoroi chlen vyrazheniya predstavlyaet soboi skorost' poteri energii gazom. My predpolagaem, chto eta energiya v konechnom itoge prevratilas' v teplo i byla izluchena, tak chto skorost' dissipacii v edinice poverhnosti diska (uchityvaya, chto disk imeet dve storony), est':

$$D(r) = \frac{G\Omega^\prime}{4\pi r} = \frac{9}{8} \nu\Sigma\Omega^2\,,$$ (64)

gde my predpolagaem keplerovskii profil' uglovoi skorosti. Dlya izlucheniya absolyutno chernogo tela D(r) = σTdiska4. Delaya podstanovku dlya Sigma i ispol'zuya dlya u S stacionarnoe reshenie, poluchennoe iz uravneniya (62), poluchim:

$$T_{\mathrm{disk}}^4 = \frac{3GM_*\dot M}{8\pi\sigma r^3} \left( 1-\sqrt{\frac{r_*}{r}\,}\right)\,. $$ (65)

Zametim, chto

  1. Vdali ot granichnogo sloya (r>>r*) temperaturnyi profil' aktivnogo akkrecionnogo diska Tdiska ∝ r-3/4. T.e. on imeet tu zhe formu, chto i dlya passivnogo akkrecionnogo diska, davaemuyu uravneniem (28)
  2. Temperaturnyi profil' ne zavisit ot vyazkosti. Eto yavlyaetsya privlekatel'noi osobennost'yu teorii pri dannoi neopredelennosti proishozhdeniya i neizvestnoi effektivnosti perenosa uglovogo momenta diska, hotya, s drugoi storony, eto lishaet nas mnozhestva vozmozhnyh putei izucheniya osnovnoi fiziki putem nablyudeniya stacionarnyh diskov.

Dlya skorosti akkrecii, ravnoi , my poluchim dlya zvezdy solnechnoi massy na rasstoyanii 1 a.e. effektivnuyu temperaturu diska, ravnuyu 150K. Eto – poverhnostnaya temperatura. Kak my pokazhem nizhe, central'naya temperatura dolzhna byt' sushestvenno vyshe.

4. Prichina perenosa uglovogo momenta

V protoplanetnom diske mozhno prenebrech' molekulyarnoi vyazkost'yu. Dlya gaza, v kotorom dlina svobodnogo probega molekul est' lambda, vyazkost'

$$\nu \sim \lambda c_s\,, $$ (66)

gde ss – skorost' zvuka. Dlina svobodnogo probega opredelyaetsya kak λ = 1/nσ, gde n – koncentraciya molekul gaza, σ – sechenie ih vzaimodeistviya. Eti velichiny legko vychislyayutsya. Naprimer, rassmotrim protoplanetnyi disk s poverhnostnoi plotnost'yu Σ=1000 g/sm2, h/r=0.05 dlya 1 a.e. Plotnost' v seredine (v central'noi ploskosti) diska po poryadku velichiny ravna n ~ Σ/ (2 mH h) = 4 x 1014 sm-3, togda kak skorost' zvuka svyazannaya s h/r ravna 1.5 km/sek. Schitaya sechenie vzaimodeistviya blizkim k ploshadi molekuly vodoroda (σ ~ 10-15 sm2), poluchim:

$$\lambda \sim 2.5~\textrm{sm,}$$
$$\nu \sim 4\times10^5 \textrm{sm}^2/\textrm{s.}$$		 (67)

Svyazannoe s etimi velichinami harakternoe vremya evolyucii diska, ravnoe τ = r2/ν, sostavlyaet po poryadku velichiny 1013 let, chto v 106 raz bol'she nablyudaemogo vremeni evolyucii diskov.

V svoei klassicheskoi rabote Shakura i Syunyaev (1973) otmetili, chto turbulentnost' v diske mozhet obespechit' effektivnuyu vyazkost', kotoraya budet gorazdo bol'she molekulyarnoi vyazkosti. Dlya izotropnoi turbulentnosti maksimal'nyi razmer yacheiki turbulentnosti v diske po poryadku velichiny budet raven tolshine diska h, togda kak maksimal'naya skorost' turbulentnogo dvizheniya budet sravnima so skorost'yu zvuka c (eshe bol'shaya skorost' privela by k poyavleniyu udarnyh voln i bystromu rasseyaniyu kineticheskoi energii turbulentnyh dvizhenii v vide tepla). Motiviruyas' etimi soobrazheniyami, Shakura i Syunyaev (1973) predlozhili parametrizaciyu:

$$\nu = \alpha c_s h\,,$$ (68)

gde α – bezrazmernyi parametr, kotoryi pokazyvaet, naskol'ko effektivno turbulentnost' privodit k perenosu uglovogo momenta. Zametim, chto sushestvovanie turbulencii v diske apriori ne daet garantiyu, chto proizoidet perenos uglovogo momenta naruzhu.

V standartnoi teorii tak nazyvaemyh "al'fa-diskov" parametr α schitaetsya konstantoi. Esli eto tak, stanovitsya vozmozhnym analiticheskoe reshenie dlya vertikal'noi struktury aktivnogo akkrecionnogo diska i vyvedenie ν kak funkcii r, Σ i α. Detali etogo processa mozhno naiti u Frank, King & Raine (2002) Kombiniruya izvestnuyu formu funkcii dlya ν s uravneniem evolyucii diska (47), mozhno poluchit' polnuyu teoriyu dlya predskazaniya vremeni evolyucii diska, s edinstvennym neizvestnym, yavlyayushimsya sootvetstvuyushei velichinoi α. Vse eto ochen' horosho, no net fizicheskih prichin polagat' α konstantoi, a esli vmesto etogo schitat' ee svobodnoi funkciei, to bol'shaya chast' zamanchivoi prostoty teorii utrachivaetsya. Modeli "al'fa-diskov" dolzhny rassmatrivat'sya skoree kak illyustracii, nezheli pryamye predskazaniya evolyucii diskov.

Chtoby pryamo ocenit', kak velika al'fa, nuzhno uchest' nablyudaemuyu evolyuciyu protoplanetnyh diskov. Predpolozhim, naprimer, chto shkala vremeni evolyucii na 50 a.e. sostavlyaet 1 million let. Togda nachinaya deistvovat' po al'fa-receptu (uravnenie 68) i zametiv, chto cs~ hΩ, poluchim vyrazhenie dlya vremeni evolyucii:

$$\tau = \frac{r^2}{\nu} = \left(\frac{h}{r}\right)^{-2} \frac{1}{\alpha\Omega}\,. $$ (69)

Sdelav podstanovku dlya tau i r i snova dopuskaya, chto h/r ~ 0.05, poluchim ocenku dlya α = 0.02. Eta velichina dostatochno tipichna – popytki nablyudatel'no ogranichit' al'fu na krupnyh masshtabah v protoplanetnyh diskah (ni odna iz etih popytok ne yavlyaetsya namnogo bolee slozhnoi, chem nashi syrye ocenki) privodyat k ocenkam ~10-2 (Hartmann et al., 1998)***. Eti znacheniya po poryadku velichiny men'she, chem znachenie α, poluchennoe pri modelirovanii vspyshek karlikovyh novyh, kotorye proishodyat v akkrecionnom diske vokrug belogo karlika (Cannizzo, 1993).

***[Vazhnym isklyucheniem yavlyaetsya modelirovanie moshnyh vzryvnyh sobytii, izvestnyh kak vspyshki ob'ektov tipa FU Oriona (fuorov), kotorye (esli ih interpretirovat' kak samoreguliruyushuyusya teplovuyu neustoichivost') trebuyut men'shih znachenii al'fa, ravnyh po poryadku velichiny 10-3 i men'she (Bell & Lin, 1994).]

Nesmotrya na real'nyi progress, sohranyayutsya opredelennye somneniya otnositel'no fizicheskoi prichiny i svoistv perenosa uglovogo momenta v protoplanetnom diske. Chislo Reinoldsa dlya techeniya v diske:

$$\textrm{Re} \equiv \frac{UL}{\nu}\,, $$ (70)

gde U – harakternaya skorost' i L – harakternyi razmer, chrezmerno veliko (po poryadku velichiny ravno 1014, esli brat' te zhe parametry, chto my ispol'zovali, rasschityvaya velichinu molekulyarnoi vyazkosti). Na Zemle techenie stanovitsya turbulentnym pri kriticheskom chisle Reinol'dsa, po poryadku velichiny ravnom 104, tak chto intuiciya podskazyvaet, chto techeniya v protoplanetnom diske dolzhny byt' sil'no turbulentny chisto iz gidrodinamicheskih effektov. Detal'noe izuchenie, odnako, ne podtverzhdaet etot vyvod. Dlya nachala zametim, chto uslovie dlya lineinoi gidrodinamicheskoi ustoichivosti v differencial'no vrashayushemsya potoke (kriterii Releya) – uvelichenie sobstvennogo uglovogo momenta pri dvizhenii naruzhu:

$$\frac{d}{dr}(r^2\Omega) > 0\,. $$ (71)

V keplerovskom diske r2Ω ∝ r1/2, tak chto potok vsegda lineino ustoichiv.

Sushestvuet ogromnoe kolichestvo literatury, v kotoroi issledovalas' vozmozhnost' nelineinoi neustoichivosti, kotoraya mozhet privesti k turbulencii v akkrecionnom diske. Na dannyi moment net nikakogo bezuslovnogo svidetel'stva togo, chto takaya neustoichivost' sushestvuet, i chislennye eksperimenty pokazali, chto gidrodinamicheskie vozmusheniya v potoke keplerovskogo diska – kotorye mogut pri nekotoryh obstoyatel'stvah pokazat' sushestvennyi vremennyi rost (Afshordi, Mukhopadhyay & Narayan, 2005; Ioannou & Kakouris, 2001) – v konechnom itoge raspadayutsya (Balbus & Hawley, 2006; Balbus, Hawley & Stone, 1996; Shen, Stone & Gardiner, 2006). Eksperimenty privodyat k pohozhim vyvodam (Ji et al., 2006). Podobnye vihri, kotorye v strogo dvumernyh modelyah diska yavlyayutsya dolgovechnymi i sposobny perenosit' uglovoi moment (Godon & Livio, 1999; Johnson & Gammie, 2005), v trehmernyh modelyah stanovyatsya podverzheny razrushitel'noi neustoichivosti (po krainei mere okolo central'noi ploskosti diska, dlya bol'shih z situaciya bolee blagopriyatna) (Barranco & Marcus, 2005; Shen, Stone & Gardiner, 2006). I, nakonec, konvekciya, kotoraya mozhet sushestvovat' v nekotoryh oblastyah protoplanetnogo diska, perenosit uglovoi moment vnutr' – i v rezul'tate ne mozhet byt' samopodderzhivayusheisya v otsutstvii drugih istochnikov perenosa (Ryu & Goodman, 1992; Stone & Balbus, 1996).

Samogravitaciya daet protivoyadie k etomu unylomu perechnyu otricatel'nyh rezul'tatov. Dostatochno massivnyi disk neustoichiv (Toomre, 1964) k razvitiyu spiral'nyh rukavov, kotorye perenosyat uglovoi moment naruzhu. My obsudim fiziku, lezhashuyu v osnove etoi neustoichivosti, pozzhe, kogda budem obsuzhdat' model' diskovoi neustoichivosti dlya formirovaniya planet–gigantov, no seichas otmetim, chto neustoichivost' voznikaet, kogda

$$\frac{M_{\mathrm{disk}}}{M_*} > \frac{h}{r}\,. $$ (72)

Samogravitaciya mozhet igrat' rol' v protoplanetnom diske na rannih etapah, kogda disk dostatochno massiven, no ona ne vazhna vposledstvii, kogda Mdiska<< Mstar.

Vozvrashayas' k nesamogravitiruyushim diskam, zametim, chto usloviya gidrodinamicheskoi ustoichivosti, dannye v uravnenii (71), dramaticheski menyayutsya v prisutstvii dazhe slabogo magnitnogo polya. Prinimaya vo vnimanie, chto gidrodinamicheskii potok ustoichiv, tol'ko kogda sobstvennyi uglovoi moment uvelichivaetsya naruzhu, magnitogidrodinamicheskii potok dlya ustoichivosti nuzhdaetsya v tom, chtoby uglovaya skorost' sama byla vozrastayushei funkciei radiusa (Balbus & Hawley, 1991; Chandrasekhar, 1961; Velikhov, 1959)***:

$$\frac{d}{dr}(\Omega^2) > 0\,,$$ (73)

***[Znachenie rezul'tata Chandrasekara dlya proishozhdeniya turbulencii v protoplanetnom diske bylo vysoko oceneno Safronovym (1969), kotoryi zametil, chto kriterii magnitogidrodinamicheskoi ustoichivosti ne perehodit v kriterii Releya pri magnitnom pole, stremyashemsya k nulyu, i chto "dlya slabogo magnitnogo polya oblako dolzhno byt' menee ustoichivo, chem my nashli ranee v otsutstvii polya". Vazhnost' magnitorotacionnoi neustoichivosti dlya akkrecionnyh diskov byla ocenena po dostoinstvu lish' spustya 20 let Balbusom i Holli (Balbus & Hawley).]

Uslovie (73) v keplerovskom diske ne vypolnyaetsya. Kak sledstvie, v ideale (koefficient diffuzii, ravnyi nulyu) magnitogidrodinamiki pri proizvol'no slabom magnitnom pole dostatochno, chtoby privnesti v keplerovskii disk lineinuyu neustoichivost', s vozmusheniyami, eksponencial'no rastushimi za dinamicheskoe vremya. Vsestoronnii obzor fiziki etoi neustoichivosti – nazyvaemoi magnitorotacionnoi – ili neustoichivost'yu Balbusa–Holli byl vypolnen Balbus & Hawley (1998). Magnitorotacionnaya neustoichivost' yavlyaetsya lineinoi i privodit k samopodderzhivayusheisya turbulencii v horosho ionizovannom akkrecionnom diske (Brandenburg et al., 1995; Stone et al., 1996). Ona perenosit uglovoi moment naruzhu, massu potoka – vnutr', i osvobozhdaet gravitacionnuyu potencial'nuyu energiyu. Magnitorotacionnaya neustoichivost' ne vsegda deistvuet podobno "al'fa–vyazkosti" (Pessah, Chan & Psaltis, 2006), no, soglasno chislennomu modelirovaniyu, grubo ekvivalentna ei i obychno privodit k effektivnosti perenosa poryadka α ~ 10-2 – podobno velichinam, vyvedennym dlya protoplanetnyh diskov, no men'she, chem oni zhe, predpolagaemye dlya diskov vokrug belyh karlikov (vspyshki karlikovyh novyh zvezd).

5. Sloistye diski

Kak polagaet bol'shinstvo, magnitorotacionnaya neustoichivost' – samaya vazhnaya (a vozmozhno, i edinstvennaya) prichina perenosa uglovogo momenta v akkrecionnyh diskah vokrug belyh karlikov, neitronnyh zvezd i chernyh dyr. Odnako v protoplanetnyh diskah voznikaet interesnoe oslozhnenie, svyazannoe s tem, chto nizkaya stepen' ionizacii gaza privodit k konechnoi provodimosti. Udel'noe soprotivlenie (ili drugie otkloneniya ot ideal'noi magnitogidrodinamiki, takie kak ambipolyarnaya diffuziya ili effekt Holla) mozhet togda potencial'no zaglushit' magnitorotacionnuyu neustoichivost', podavit' turbulentnost' i svyazannyi s neyu perenos uglovogo momenta. Lineinaya fizika v etom rezhime byla proanalizirovana v mnogochislennyh rabotah, vklyuchaya raboty Blaes & Balbus (1994), Desch (2004) and Salmeron & Wardle (2005), k kotorym my i napravlyaem chitatelei. Zdes' ya obrisuyu bolee shirokuyu kartinu, osnovannuyu na prostoi fizike, kotoraya byla predlozhena Gammie (1996) kak model', dlya kotoroi magnitorotacionnaya neustoichivost' mogla by rabotat' v protoplanetnyh diskah. Ya podcherkivayu, chto v otlichie ot predydushego obsuzhdeniya osnovnyh principov magnitorotacionnoi neustoichivosti, eto primenenie k protoplanetnym diskam ostaetsya neskol'ko umozritel'nym.

Sleduya Gammi (Gammie), my nachnem s zamechaniya, chto v prisutstvii udel'nogo soprotivleniya (predpolagaya, chto imenno ono yavlyaetsya samym glavnym effektom neideal'nosti, narushayushim magnitorotacionnuyu neustoichivost'), magnitnoe pole podchinyaetsya obychnomu uravneniyu indukcii:

$$\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) - \nabla \times (\eta\nabla \times \mathbf{B})\,, $$ (74)

gde η – magnitnyi koefficient diffuzii. S drugoi storony, η mozhet byt' zapisana v terminah stepeni ionizacii x = ne/nH:

$$\eta = 6.5 \times 10^{-3} x^{-1} \textrm{sm}^2/\textrm{s.} $$ (75)

Nasha cel' sostoit v opredelenii minimal'nogo znacheniya x, dlya kotorogo magnitorotacionnaya neustoichivost' eshe budet rabotat', nesmotrya na zatuhanie, vyzvannoe udel'nym soprotivleniem. Delaya eto, my zametim, chto udel'noe soprotivlenie legche vsego podavlyaet magnitorotacionnuyu neustoichivost' na malyh masshtabah. Poetomu my rassmotrim v diske elementy naibol'shih razmerov l = h, i priravnyaem harakternoe vremya rosta vozmushenii vsledstvie magnitogidrodinamicheskoi neustoichivosti (Balbus & Hawley, 1998):

$$\tau_{\mathrm{MRI}} \sim \frac{h}{v_A}\,,$$ (76)

gde vA = (B2/4πρ)1/2 – skorost' al'venovskih voln, k harakternomu vremeni zatuhaniya:

$$\tau_{\mathrm{zatuh}} \sim \frac{h^2}{\eta}\,. $$ (77)

Takim obrazom, my poluchim prostoi kriterii dlya srabatyvaniya magnitorotacionnoi neustoichivosti:

$$\eta < h v_A\,. $$ (78)

Ostaetsya ocenit' sootvetstvuyushie velichiny h i vA. Dlya gruboi ocenki my mozhem predpolozhit', chto pri 1 a.e. h = 1012 sm i vA ~ c ~ 105 sm/sek (bolee tochno vA ~ α1/2cs, gde α – koefficient magnitogidrodinamicheskoi turbulencii, analogichnyi al'fe Shakury–Syunyaeva). V etom sluchae predel magnitnogo koefficienta diffuzii η < 1017 sm2/sek, kotoryi sootvetstvuet minimal'noi stepeni ionizacii

$$x > 10^{-13}\,, $$ (79)

kotoraya bolee menee sovpadaet s velichinoi, poluchennoi iz bolee strogogo analiza (Balbus & Hawley, 1998; Gammie 1996).

Stoit otmetit' ochen' vazhnuyu vesh' – eta stepen' ionizacii yavlyaetsya ochen' malen'koi! Lineinyi rost vozmushenii vsledstvie magnitorotacionnoi neustoichivosti okazyvaetsya nastol'ko bystrym, chto dazhe kroshechnaya stepen' ionizacii dostatochno horosho "prikleivaet" gaz k magnitnomu polyu i preodolevaet stabiliziruyushee deistvie udel'nogo soprotivleniya.

Hotya dlya raboty magnitorotacionnoi neustoichivosti trebuetsya sovsem malaya stepen' ionizacii, v protoplanetnom diske mogut byt' oblasti, gde i takaya stepen' ionizacii mozhet byt' ne dostignuta. Nuzhno rassmotret' dva istochnika ionizacii:

  1. Ionizaciya pri stolknoveniyah. Vychisleniya Umebayashi (1983) pokazali, chto ionizaciya shelochnyh metallov dostatochna dlya podderzhaniya x > 10-13. Eto proishodit pri temperaturah poryadka 1000K i vyshe. Oblast' samoi vnutrennei chasti diska – v predelah neskol'kih desyatyh a.e. ot zvezdy – dolzhna byt' v sostoyanii podderzhivat' magnitorotacionnuyu neustoichivost' v rezul'tate prosto teplovoi ionizacii.
  2. Ionizaciya kosmicheskimi luchami. Kosmicheskie luchi pogloshayutsya sloem veshestva s poverhnostnoi plotnost'yu 100 g/sm2. (Umebayashi & Nakano, 1981). Oni ioniziruyut vsyu tolshu diska dostatochno horosho, chtoby magnitorotacionnaya neustoichivost' zarabotala na bol'shih rasstoyaniyah ot zvezdy, gde poverhnostnaya plotnost' gaza men'she dvuh kriticheskih, i ionizuyut poverhnostnyi sloi s plotnost'yu, ravnoi kriticheskoi, na men'shih rasstoyaniyah.
Risunok 14. Shematicheskii risunok modeli sloistogo diska, predstavlennyi Gammie (1996). V etoi modeli vnutrennyaya chast' diska dostatochno goryacha, chtoby teplovaya ionizaciya "prikleila" gaz k magnitnomu polyu i dopustila razvitie magnitorotacionnoi neustoichivosti. Na bol'shih rasstoyaniyah ot zvezdy kosmicheskie luchi pronikayut na vsyu tolshinu diska i obespechivayut neobhodimuyu ionizaciyu. Veroyatno, chto na srednih (promezhutochnyh) rasstoyaniyah akkreciya proishodit v aktivnom poverhnostnom sloe s plotnost'yu ~100 g/sm2, kotoryi ionizovan kosmicheskimi luchami. Vnutri etogo sloya raspolozhena neaktivnaya "mertvaya zona", v kotoroi razvitie magnitorotacionnoi neustoichivosti podavleno i pochti net turbulentnosti.

Esli net drugih istochnikov ionizacii, to na rasstoyaniyah, gde disk dostatochno prohladen, chtoby ne ionizirovat'sya pri stolknoveniyah atomov i molekul gaza, i dostatochno ploten, chtoby v nego ne pronikali kosmicheskie luchi, my mogli by ozhidat' novuyu strukturu ("mertvuyu zonu"), v kotoroi disk vblizi svoei central'noi ploskosti byl by nepodvizhnym, i tol'ko poverhnostnyi sloi byl by magnitno aktivnym i podderzhival akkreciyu (Gammie, 1996). Model' takogo sloistogo diska predstavlena na Risunke 14.

Modeli sloistyh diskov kachestvenno otlichayutsya ot obychnyh polnost'yu vyazkih diskov v dvuh vazhnyh aspektah. Vo-pervyh, potok massy cherez aktivnyi sloi est' funkciya (po analogii s uravneniem 62) vyazkosti i glubiny kolonki νsloyaΣsloya aktivnogo sloya, kotoraya ne zavisit ot polnoi poverhnostnoi plotnosti diska na etom rasstoyanii ot zvezdy. Mozhno predskazat', chto kolichestvo massy, kotoruyu aktivnyi sloi mozhet propustit' cherez sebya, yavlyaetsya padayushei funkciei rasstoyaniya do zvezdy, takim obrazom, gaz, vtekayushii vnutr' iz vneshnih sloev diska, vybyvaet iz potoka i nakaplivaetsya v mertvoi zone. V etom sluchae uzkoe mesto ("butylochnoe gorlyshko") pri akkrecii na zvezdu nahoditsya na vnutrennem krae sloistoi chasti diska. Potok massy cherez etu oblast' ocenivaetsya po poryadku velichiny v 10-8 mass Solnca v god, chto soglasuetsya s nablyudeniyami zvezd tipa T Tel'ca solnechnoi massy (Gammie, 1996). Odnako predskazannyi potok massy dolzhen byt' primerno konstantoi i ne zaviset' ot massy zvezdy, chto ne soglasuetsya (Alexander & Armitage, 2006) s ochevidnym uvelicheniem srednei skorosti akkrecii v zavisimosti ot massy zvezdy:

$$\dot M \propto M_*^2\,,$$ (80)

chto bylo vyvedeno iz nablyudenii kak zvezdnyh, tak i subzvezdnyh ob'ektov (Mohanty, Jayawardhana & Basri, 2005).

Vo-vtoryh, sloistye modeli predskazyvayut, chto oblast' vblizi central'noi ploskosti diska dolzhna byt' nepodvizhna v tochnosti na teh rasstoyaniyah ot zvezdy, kotorye predstavlyayut naibol'shii interes s tochki zreniya formirovaniya planet. Eto imeet vazhnoe znachenie dlya osedaniya pyli, dlya posleduyushego rosta planetezimalei i dlya migracii malomassivnyh planet (Matsumura & Pudritz, 2005). Vozmozhna takzhe prichastnost' sloistoi modeli k ob'yasneniyu peremennosti molodyh zvezd, tak kak rastushaya mertvaya zona obespechivaet rezervuar gaza na malyh rasstoyaniyah ot zvezdy, gde on v principe mozhet byt' nagret i ionizirovan, privodya k vspyshkam akkrecii (Armitage, Livio & Pringle, 2001).

Sloistye diski dayut nam interesnye vozmozhnosti, odnako sushestvuyut li oni v deistvitel'nosti? V nastoyashee vremya sushestvuet neskol'ko nablyudatel'nyh ogranichenii na ih sushestvovanie, hotya teoreticheski ideya ostaetsya vozmozhnoi. Chislennoe modelirovanie (Sano & Stone, 2002) podtverdilo, chto, kogda magnitnoe chislo Reinoldsa (ocenennoe v podhodyashem masshtabe diska):

$$\textrm{Re}_M \equiv \frac{v_A^2}{\eta\Omega} $$ (81)

padaet nizhe kriticheskogo znacheniya, lezhashego v oblasti mezhdu 1 i 30, turbulenciya, voznikayushaya iz razvitiya magnitorotacionnoi neustoichivosti, okazyvaetsya podavlennoi. Eto shiroko soglasuetsya s prostymi argumentami, privedennymi vyshe, i privodit k toi zhe kriticheskoi stepeni ionizacii. Odnako neobhodimo kraine malo energii dlya togo, chtoby podderzhivat' dostatochnyi uroven' ionizacii dlya razvitiya magnitorotacionnoi neustoichivosti, i bylo predlozheno, chto energii turbulencii dostatochno dlya podderzhaniya ionizacii i magnitorotacionnoi neustoichivosti aktivnogo diska (Inutsuka & Sano, 2005). Drugaya vozmozhnost', podtverzhdennaya nedavnim chislennym modelirovaniem Turner, Sano & Dziourkevitch (2006), zaklyuchaetsya v tom, chto turbulentnoe peremeshivanie sposobno perenesti dostatochno zaryadov iz poverhnostnogo sloya k central'noi ploskosti diska i obespechit' tam ne ravnyi nulyu perenos veshestva. Uchityvaya eti teoreticheskie somneniya, vopros, imeyut li protoplanetnye diski strukturu, podobnuyu ukazannoi na Risunke 14, ostaetsya otkrytym. Kriticheskii vopros – sushestvuyut li v dostatochnyh kolichestvah malen'kie zerna (pylinki), smeshannye s gazom, chtoby effektivno pogloshat' svobodnye elektrony.

6. Rasseyanie diska

Utrata gazovoi komponenty protoplanetnyh diskov nakladyvaet vremennoi predel na zavershenie processa formirovaniya planet–gigantov i menyaet okruzhayushuyu sredu pri formirovanii planet zemnogo tipa. Samopodobnoe reshenie uravneniya evolyucii vyazkih diskov (formula 57) predskazyvaet, chto poverhnostnaya plotnost' i skorost' akkrecii umen'shayutsya na pozdnih vremenah po stepennomu zakonu, i, sledovatel'no, perehod mezhdu diskom i bezdiskovym sostoyaniem dolzhen byt' postepennym. Odnako etogo ne nablyudaetsya. Molodye zvezdy so svoistvami, promezhutochnymi mezhdu "klassicheskimi zvezdami tipa T Tel'ca" i "obnazhennymi zvezdami tipa T Tel'ca", otnositel'no redki i sostavlyayut primerno 10% ot polnoi populyacii zvezd, kotorye demonstriruyut, po krainei mere, odin priznak okolozvezdnogo diska. Soglasno etoi statistike, mozhno sdelat' vyvod, chto harakternoe vremya rasseyaniya diska neveliko i sostavlyaet ~105 let (Simon & Prato, 1995; Wolk & Walter, 1996).

Klyuchevoi mehanizm, kotoryi mozhet privodit' k rasseyaniyu diska, byl obnaruzhen s pomosh'yu nablyudenii kosmicheskim teleskopom im. Habbla malomassivnyh zvezd, osveshennyh sil'nym ioniziruyushim izlucheniem, ispuskaemym massivnymi zvezdami v yadre Tumannosti Oriona v skoplenii Trapeciya (O'Dell, Wen & Hu, 1993). Izobrazheniya pokazyvayut tumannosti v forme golovastika, okruzhayushie molodye zvezdy s okolozvezdnymi diskami, kotorye interpretiruyutsya kak fotoisparenie i uletuchivanie gaza iz diska v rezul'tate osvesheniya vneshnim ioniziruyushim izlucheniem (Johnstone, Hollenbach & Bally, 1998). Osnovnaya fizika etogo processa otnositel'no prosta (Bally & Scoville, 1982; Hollenbach et al., 1994; Shu, Johnstone & Hollenbach, 1993) i tesno svyazana s horosho izuchennoi problemoi vetrov, nagretyh komptonovskim izlucheniem, v akkrecionnyh diskah aktivnyh yader galaktik (Begelman, McKee & Shields, 1983). Zhestkie ul'trafioletovye kvanty*** s energiei >13.6 eV ioniziruyut i nagrevayut poverhnostnyi sloi diska, povyshaya ego temperaturu do 104 K, harakternuyu dlya HII oblastei.

*** [Ul'trafioletovye kvanty s energiei 6 eV < E <13.6 eV takzhe mogut igrat' vazhnuyu rol'. Ul'trafioletovoe izluchenie, dostatochnoe dlya dissociacii molekul vodoroda, takzhe mozhet privodit' k utekaniyu gaza vo vneshnih chastyah diska, gde skorost' vrasheniya men'she. Detal'naya fizika takih potokov – kotorye bol'she napominayut oblasti fotodissociacii, nezheli oblasti HII – tyazhela dlya vychislenii, potomu chto temperatura goryachego gaza opredelyaetsya balansom mezhdu fotoelektricheskim nagrevom i ohlazhdeniem putem izlucheniya atomnyh i molekulyarnyh linii. Adams i dr. (2006) rassmotrel poteryu massy diskov iz-za vneshnego ul'trafioletovogo izlucheniya v svoih modelyah evolyucii diskov v skopleniyah, odnako eto vetry, vyzvannye izlucheniem dal'nego ul'trafioleta, kotorye bolee vazhny dlya effektivnogo i bystrogo rasseyaniya diska v konce fazy "klassicheskoi zvezdy tipa T Tel'ca".]

Skorost' zvuka v fotoionizirovannom gaze sostavlyaet cs ~ 10 km/sek. Za predelami kriticheskogo radiusa, opredelennogo kak

$$r_g = \frac{GM_*}{c_s^2}\,,$$ (82)

skorost' zvuka v goryachem gaze prevyshaet lokal'nuyu keplerovskuyu skorost'. V etom sluchae gaz stanovitsya nesvyazannym i vytekaet iz diska kak teplovoi veter. Dlya zvezdy solnechnoi massy kriticheskii radius ocenivaetsya v 9 a.e.

Etot zhe samyi process mozhet proizoiti nezavisimo ot togo, prihodit li ul'trafioletovoe izluchenie iz vneshnego istochnika, takogo kak massivnaya zvezda v skoplenii, ili neposredstvenno ot central'noi zvezdy. Odnako v tipichnoi oblasti zvezdoobrazovaniya (Lada & Lada, 2003) bol'shinstvo malomassivnyh zvezd poluchaet slishkom malo ul'trafioletovogo izlucheniya iz vneshnih istochnikov dlya togo, chtoby ih diski razrushilis' (Adams et al., 2006). Poetomu veroyatnee, chto fotoisparenie proizoidet iz–za izlucheniya central'noi zvezdy. V etom rezhime Hollenbach et al. (1994) poluchil ocenku skorosti poteri massy putem fotoispareniya:

$$\dot M_{\mathrm{wind}} \simeq 4\times10^{-10} \left(\frac{\Phi}{10^{41}\,\textrm{c}^{-1}}\right)^{1/2} \left(\frac{M_*}{M_\odot}\right)^{1/2} M_\odot/\textrm{god,} $$ (83)

gde Φ – potok zvezdnogo sveta, sposobnogo ionizirovat' gaz. Bylo predskazano, chto bol'shaya chast' poteri massy cherez veter proizoidet vblizi rg, s radial'noi zavisimost'yu tempa poteri massy: $\dot\Sigma \propto r^{-5/2}$. Gidrodinamicheskoe chislennoe modelirovanie, provedennoe Font et al. (2004), v znachitel'noi stepeni podtverzhdaet etu osnovnuyu kartinu, hotya v detalyah bylo naideno, chto poterya massy proishodit i pri rasstoyaniyah ot zvezdy, men'shih kriticheskogo radiusa, a polnyi temp poteri massy neskol'ko men'she predskazannogo uravneniem (83).

Sochetanie fotoisparitel'nogo vetra i evolyucii vyazkogo diska privodit k bystromu rasseyaniyu diska (Clarke, Gendrin & Sotomayor, 2001). Vychisleniya Alexander, Clarke & Pringle (2006) predlagayut trehstupenchatyi scenarii, shematicheski predstavlennyi na Risunke 15:

  1. Snachala . Poterya massy cherez "diskovyi veter" okazyvaet neznachitel'noe vliyanie na disk, kotoryi evolyucioniruet kak v obychnyh vyazkih modelyah. Skorost' akkrecii i poverhnostnaya plotnost' postepenno ponizhayutsya v vyazkoi shkale vremeni vsego diska (opredelennoi na bol'shih rasstoyaniyah ot zvezdy), kotoraya po poryadku velichiny ravna millionu let.
  2. Cherez neskol'ko millionov let skorost' akkrecii umen'shaetsya tak, chto . Diskovyi veter stanovitsya togda dostatochno sil'nym, chtoby opredelyat' evolyuciyu poverhnostnoi plotnosti diska vblizi kriticheskogo radiusa, privesti k poyavleniyu promezhutka (sheli) v diske i otklyuchit' vnutrennii disk ot popolneniya gazom iz vneshnih, udalennyh ot zvezdy oblastei diska.
  3. Kak tol'ko vnutrennii disk okazyvaetsya lishen gaza, ostavshiisya gaz vo vneshnei chasti diska stanovitsya neposredstvenno osveshen ul'trafioletovym svetom zvezdy (a pered etim on osveshalsya v osnovnom svetom, rasseyannym gazom na bolee tesnyh orbitah). Etot svet bystro nagrevaet i rasseivaet ves' ostavshiisya gaz.
Glavnyi istochnik neopredelennosti v etih modelyah – proishozhdenie i velichina potoka zvezdnogo ioniziruyushego izlucheniya. Est' nemnogo ogranichenii na velichinu potoka dlya zvezd tipa T Tel'ca solnechnoi massy, i pochti net informacii dlya zvezd drugih mass.
Risunok 15. Shematicheskaya illyustraciya togo, kak fotoisparenie, vyzvannoe central'nym istochnikom ul'trafioletovogo izlucheniya, rasseivaet protoplanetnyi disk. V nachal'nyi moment ul'trafioletovoe izluchenie (pokazannoe krasnymi strelkami) ioniziruet poverhnost' diska, privodya k vertikal'nomu rasshireniyu svyazannoi atmosfery diska pri r < rg, i potere massy putem teplovogo "diskovogo" vetra pri i>r > rg. Potok ioniziruyushego izlucheniya, kotoryi zastavlyaet isparyatsya vneshnii disk, voznikaet putem rasseyaniya fotonov zvezdnogo izlucheniya diskom na malyh rasstoyaniyah ot zvezdy ("diffuznoe pole"). Cherez neskol'ko millionov let temp akkrecii v diske padaet do velichin, sravnimyh so skorost'yu poteri massy cherez "diskovyi veter". V etot moment veter privodit k poyavleniyu v diske promezhutka (sheli) vblizi kriticheskogo radiusa, otrezayushego vnutrennii disk ot popolneniya zapasov veshestva iz vneshnih sloev diska. Vnutrennii disk togda bystro stekaet na zvezdu – privodya k poyavleniyu "vnutrennei dyry" – i pryamoe ul'trafioletovoe izluchenie zvezdy bystro rasseivaet vneshnie oblasti diska.

G. Posledovatel'nost' kondensacii

V aktivnom akkrecionnom diske dolzhen sushestvovat' temperaturnyi gradient po vertikal'noi osi z dlya energii, kotoraya perenositsya ot plotnoi central'noi ploskosti diska k fotosfere, gde ona osvobozhdaetsya i izluchaetsya (zametim, chto dlya tonkogo diska s h/r << 1 gradient po z budet dominirovat' nad radial'nym gradientom, kotorym mozhno prenebrech'). Prostoe primenenie teorii perenosa izlucheniya v ploskoparallel'nom sluchae (Rybicki & Lightman, 1979) pozvolyaet nam poluchit' otnoshenie mezhdu central'noi temperaturoi diska Tc i effektivnoi temperaturoi diska Tdisk.

Prodolzhaya, opredelim opticheskuyu tolshinu v central'noi ploskosti diska

$$\tau = \frac{1}{2} \kappa_R \Sigma\,,$$ (84)

gde kR – srednyaya neprozrachnost' Rosselanda, Σ – poverhnostnaya plotnost' diska. Vertikal'nyi profil' plotnosti diska est' ρ(z). Esli vertikal'nyi perenos energii proishodit putem diffuzii izlucheniya (v nekotoryh oblastyah takzhe mozhet byt' vazhna konvekciya), togda dlya τ >> 1 vertikal'nyi potok energii daetsya uravneniem diffuzii izlucheniya:

$$F(z)= -\frac{16\sigma T^3}{3\kappa_R\rho} \frac{dT}{dz}\,.$$ (85)

Davaite predpolozhim dlya prostoty, chto vsya dissipaciya energii proishodit pri z=0. ***

*** [Otmechu, chto dlya diskov, v kotoryh aktivna magnitorotacionnaya neustoichivost', chislennoe modelirovanie, provedennoe Miller & Stone (2000), predlagaet, chto znachitel'naya dolya osvobozhdennoi energii perenositsya k bol'shim z i rasseivaetsya v oblastyah s namnogo men'shei opticheskoi glubinoi, vozmozhno, formiruya goryachuyu koronu.]

V etom sluchae F(z) = σTdiska4 ne menyaetsya s vysotoi (ostaetsya konstantoi). Integriruem, predpolagaya, chto neprozrachnost' ostaetsya konstantoi:

$$-\frac{16\sigma}{3\kappa_R} \int_{T_c}^{T_{disk}} T^3dT = \sigma T_{\mathrm{disk}}^4 \int_0^z \rho(z')dz'$$
$$ -\frac{16\sigma}{3\kappa_R} \left[\frac{T^4}{4}\right]_{T_c}^{T_{disk}} = T_{\mathrm{disk}}^4 \frac{\Sigma}{2}\,,$$		 (86)

gde pri vyvode final'nogo uravneniya my ispol'zovali tot fakt, chto pri &taul>>1 prakticheski ves' gaz diska lezhit nizhe fotosfery. Dlya bol'shih τ my ozhidaem, chto Tc4>> Tdiska4, i uravnenie uproshaetsya do:

$$\frac{T_c^4}{T_{\mathrm{disk}}^4} \simeq \frac{3}{4}\tau\,.$$ (87)

Znachenie etogo rezul'tata zaklyuchaetsya v tom, chto aktivnye diski s bol'shoi opticheskoi glubinoi yavlyayutsya gorazdo bolee goryachimi vblizi central'noi ploskosti, nezheli na poverhnosti. Naprimer, esli τ~100, dlya teplovogo izlucheniya, ispuskaemogo diskom na nekotorom radiuse Tc~ 3  Tdiska. Eto vazhno, t.k. central'naya temperatura opredelyaet skorost' zvuka, a ta opredelyaet vyazkost' (uravnenie 68), a eshe central'naya temperatura opredelyaet, kakie l'dy i mineraly mogut tam sushestvovat'. Takim obrazom, otnositel'no skromnye urovni akkrecii mogut sushestvenno izmenit' teplovuyu strukturu diska.

I dlya formirovaniya planet zemnogo tipa, i dlya formirovaniya planet-gigantov (esli ih formirovanie proishodit putem akkrecii na yadro) predstavlyayut bol'shoi interes primes' tverdogo komponenta v diske. Gaz, formiruyushii protoplanetnyi disk, budet vklyuchat' v sebya mezhzvezdnye pylevye granuly, sostoyashie iz smesi silikatov, grafita i policiklicheskih aromaticheskih uglevodorodov (PAU). Izmerenie zavisimosti poglosheniya sveta v mezhzvezdnoi srede ot dliny volny privelo k predpolozheniyu, chto kolichestvo pylevyh granul raspredelyaetsya po stepennomu zakonu v zavisimosti ot ih razmerov (Mathis, Rumpl & Nordsieck, 1977):

$$n(a) \propto a^{-3.5}\,,$$ (88)

gde a – razmer granul (v predpolozhenii ih sferichnosti), a raspredelenie ohvatyvaet pylinki razmerom ot 0.005 do 1 mkm. Eto raspredelenie obychno yavlyaetsya otpravnoi tochkoi dlya dal'neishei evolyucii v usloviyah bol'shei plotnosti, preobladayushih v diske. V naibolee goryachih vnutrennih oblastyah diska central'naya temperatura mozhet byt' dostatochno vysoka dlya razrusheniya granul (ot 1000K do 2000K v zavisimosti ot togo, iz grafita ili silikatov sdelany pylinki). Otsutstvie pyli ochen' blizko ot zvezdy yavlyaetsya odnim iz glavnyh argumentov protiv obrazovaniya goryachih yupiterov "na meste", no radius razrusheniya pyli dostatochno mal (obychno gorazdo men'she 1 a.e.), chtoby izredka privodit' k obrazovaniyu planety zemnogo tipa ili planety–giganta. Odnako s nablyudatel'noi tochki zreniya vazhno, chto razrushenie pyli privodit k rezkomu umen'sheniyu neprozrachnosti gaza. Poetomu vo vnutrennei chasti diska budet nablyudat'sya dyra, otverstie, dazhe esli gaz budet tam prisutstvovat'.

Esli gaz, sostavlyayushii protoplanetnyi disk, imeet izvestnyi elementnyi sostav (naprimer, kak u Solnca), to eto horoshaya zadacha dlya himika – vychislit' naibolee termodinamicheski ustoichivuyu smes' himicheskih veshestv pri dannyh davlenii i temperature. Izobilie razlichnyh mineralov i l'dov v diske budet vytekat' iz etoi posledovatel'nosti kondensacii pri uslovii, chto est' dostatochno vremeni dlya dostizheniya ravnovesiya himicheskih reakcii – eto razumnoe predpolozhenie dlya goryachego vnutrennego diska, no v prohladnyh vneshnih chastyah diska vozmozhny otkloneniya vsledstvie zamedleniya himicheskih reakcii i radial'nogo dreifa gaza i pyli. Sostav ravnovesnoi smesi bol'she zavisit ot temperatury, nezheli ot davleniya, takim obrazom, my mozhem primerno nanesti na kartu posledovatel'nost' kondensacii i predskazat' izmenenie sostava diska v zavisimosti ot radiusa. Tablica II, adaptirovannaya Lodderom Lodders (2003), perechislyaet razlichnye temperatury, nizhe kotoryh dolzhny dominirovat' razlichnye l'dy i mineraly. Iz nih, bezuslovno, samaya vazhnaya – temperatura, nizhe kotoroi mozhet sushestvovat' vodnyi led – eto 180K pri davlenii 10-4 bar (hotya v usloviyah protoplanetnogo diska led kondensiruetsya pri temperature 150K). Dlya smesi solnechnogo sostava poverhnostnaya plotnost' skondensirovavshihsya materialov dramaticheski rastet s formirovaniem vodyanogo l'da:

Σ(l'da i kamnya) $\simeq$ 4Σ(kamnya), (89)

hotya eto otnoshenie zavisit ot eshe neuverennogo znaniya tochnogo solnechnogo sostava Lodders (2003). Eto zastavlyaet nas svyazyvat' izmeneniya v effektivnosti formirovaniya planet (v chastnosti, razdelenie mezhdu planetami zemnogo tipa i planetami–gigantami v Solnechnoi sisteme) so znachitel'nym izmeneniem predskazannoi poverhnostnoi plotnosti tverdyh chastic na dannom rasstoyanii ot zvezdy.

Radius protoplanetnogo diska, vne kotorogo mozhet sushestvovat' vodyanoi led, nazyvaetsya snegovoi liniei. V Solnechnoi sisteme asteroidy, bogatye l'dom, byli naideny tol'ko vo vneshnei chasti poyasa asteroidov (Morbidelli et al., 2000), chto govorit o tom, chto snegovaya liniya v protosolnechnoi tumannosti raspolagalas' okolo 3 a.e. Dlya passivnyh protoplanetnyh diskov vychislennoe raspolozhenie snegovoi linii okazyvaetsya gorazdo blizhe k zvezde – v ryade sluchaev poryadka 1 a.e. – odnako uvelichenie skorosti akkrecii do znachenii, sootvetstvuyushih klassicheskim zvezdam tipa T Tel'ca, dostatochno dlya perenosa snegovoi linii do 3 a.e.

Publikacii s klyuchevymi slovami: planety - planetnaya sistema - ekzoplaneta
Publikacii so slovami: planety - planetnaya sistema - ekzoplaneta
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [6]
Ocenka: 2.9 [golosov: 104]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya