Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << Glava I. Odnorodnaya sreda | Oglavlenie | 1.2 Stepen' vozbuzhdeniya i ionizacii >>

1.1 Osnovnye uravneniya

Pust' n_i - chislo atomov v i-m sostoyanii, n⁺- chislo ionizovannyh atomov i n_e - chislo svobodnyh elektronov v 1 sm³, sootvetstvenno. Chislo ionizacii s i-go urovnya, proishodyashih v 1 sm³ za 1 sek., my oboznachim cherez n_iB_icρ_ic, gde B_ic - einshteinovskii koefficient poglosheniya i ρ_ic - plotnost' izlucheniya za granicei i-i serii, chislo zahvatov na i-i uroven' - cherez n_en⁺C_i(T_e), gde C_i(T_e) - nekotoraya funkciya ot elektronnoi temperatury T_e, i chislo spontannyh perehodov s i-go urovnya na k-i - cherez n_iA_ik, gde A_ik - einshteinovskii koefficient spontannogo perehoda.

Esli by sreda byla nepodvizhnoi, to perehody s i-go urovnya na k-i v tochnosti uravnoveshivalis' by perehodami s k-go urovnya na i-i, tak kak vse kvanty, izluchaemye v spektral'nyh liniyah, pogloshalis' by v samoi srede. Pri nalichii zhe gradienta skorosti chislo perehodov s i-go urovnya na k-i budet bol'she chisla obratnyh perehodov, tak kak nekotoraya dolya kvantov v sootvetstvuyushei linii uidet iz sredy vsledstvie effekta Dopplera. Etu dolyu my oboznachim cherez β_ki. Togda izbytok chisla perehodov tipa i → k nad obratnymi perehodami budet raven n_iA_ikβ_ki.

V stacionarnom sostoyanii chislo perehodov atomov iz i-go sostoyaniya vo vse drugie dolzhno ravnyat'sya chislu perehodov v i-oe sostoyanie. Vsledstvie etogo my poluchaem

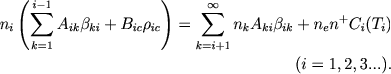
$\begin{eqnarray} n_{i}\left(\sum_{k=1}^{i-1} A_{ik} \beta_{ki} + B_{ic} \rho_{ic}\right) = \sum_{k=i+1}^{\infty} n_{k} A_{ki} \beta_{ik} + n_{e} n^{+} C_{i}(T_{i})\nonumber \\ (i=1,2,3...).\nonumber \end{eqnarray}$ (1)

V etih uravneniyah velichiny ρ_ic schitayutsya izvestnymi i ravnymi

$\begin{eqnarray} \rho_{ic}=W\rho_{ic}^*,\nonumber \end{eqnarray}$ (2)

gde ρ_ic^* - plotnost' izlucheniya za granicei i-i serii na poverhnosti zvezdy i W - koefficient dilyucii.

Prezhde vsego nam nado opredelit' velichiny β_ik. Pristupaya k etomu, my dopustim, chto kak koefficient poglosheniya, tak i koefficient izlucheniya v linii chastoty ν_ik otlichny ot nulya i postoyanny v intervale Δν_ik, ravnom

$\begin{eqnarray} \Delta\nu_{ik}=2\frac{u}{c}\nu_{ik},\nonumber \end{eqnarray}$ (3)

gde u - srednyaya termicheskaya skorost' atomov i s - skorost' sveta, i ravny nulyu vne etogo intervala. Dlya koefficienta poglosheniya v linii my imeem

$\begin{eqnarray} \alpha_{ik}=\frac{n_{i} B_{ik}}{c\Delta\nu_{ik}} \left(1-\frac{g_i}{g_k}\frac{n_k}{n_i} \right) h\nu_{ik}\nonumber \end{eqnarray}$ (4)

Kogda izluchenie, vyhodyashee iz tochki A, pridet v tochku V, nahodyashuyusya na rasstoyanii s ot A, to ono budet oslableno v e^α_iks raz i budet smesheno po chastote na velichinu

$\begin{eqnarray} \nu_{ik}^{'}-\nu_{ik}=\frac{\nu_{ik}}{c}\frac{dv}{ds}s,\nonumber \end{eqnarray}$ (5)

gde $\frac{dv}{ds}$ - gradient skorosti v srede. Sledovatel'no, iz izlucheniya, vyhodyashego iz A, budet pogloshena v srede lish' sleduyushaya chast':

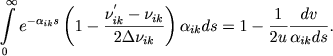
$\begin{eqnarray} \int\limits_0^\infty e^{-\alpha_{ik}s} \left(1-\frac{\nu_{ik}^{'}-\nu_{ik}}{2\Delta\nu_{ik}}\right)\alpha_{ik}ds=1-\frac{1}{2u}\frac{dv}{\alpha_{ik}ds}.\nonumber \end{eqnarray}$ (6)

Takim obrazom dlya velichiny β_ik my nahodim

$\begin{eqnarray} \beta_{ik}=\frac{1}{2u}\frac{dv}{\alpha_{ik}ds}.\nonumber \end{eqnarray}$ (7)

Naidennoe vyrazhenie dlya β_ik my dolzhny podstavit' v uravnenie (1). No legko videt', chto

$\begin{eqnarray} A_{ki}\beta_{ik}=\frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_k}{g_i}n_i-n_k}\left(\frac{\nu_{ik}}{\nu_{12}}\right)^3A_{21}\beta_{12}.\nonumber \end{eqnarray}$ (8)

Poetomu v rezul'tate podstanovki my poluchaem

$\begin{eqnarray} n_i\left[x\sum_{k=1}^{i-1} \frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_i}{g_k}n_k-n_i}\left(\frac{\nu_{ki}}{\nu_{12}}\right)^3+\frac{B_{ic}\rho_{ic}^*}{A_{21}}\right]=\nonumber\\ =x\sum_{k=i+1}^{\infty} n_k \frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_k}{g_i}n_i-n_k}\left(\frac{\nu_{ik}}{\nu_{12}}\right)^3+\frac{n_e n^+ C_i}{WA_{21}},\nonumber \end{eqnarray}$ (9)

gde oboznacheno

$\begin{eqnarray} x=\frac{\beta_{12}}{W}.\nonumber \end{eqnarray}$ (10)

Sistema uravnenii (9) polnost'yu opredelyaet stepen' vozbuzhdeniya i ionizacii v srede, t. e. velichiny $\frac{n_i}{n_1}$ i $\frac{n_e n^+}{Wn_i}$ . Parametrami, vhodyashimi v uravneniya (9), krome velichiny h, yavlyayutsya temperatura zvezdy (vhodyashaya cherez posredstvo B_icρ_ic^*) i temperatura sredy (vhodyashaya cherez posredstvo C_i). Predstavlyaet interes to obstoyatel'stvo, chto parametrom yavlyaetsya lish' otnoshenie gradienta skorosti k koefficientu dilyucii, a ne kazhdaya iz etih velichin v otdel'nosti. Eto znachit, mezhdu prochim, chto odin i tot zhe gradient skorosti skazyvaetsya na vozbuzhdenii i ionizacii tem sil'nee, chem men'she koefficient dilyuci.

Poluchennye nami uravneniya otnosyatsya k sluchayu, kogda sreda neprozrachna dlya izlucheniya vo vseh liniyah. Dopustim teper', chto sreda prozrachna v liniyah vseh serii, nachinaya s j-i. Togda, ochevidno, v nashih uravneniyah my dolzhny polozhit'

$\begin{eqnarray} \beta_{ik}=1 \quad (i=j,j+1,j+2,...).\nonumber \end{eqnarray}$ (11)

My znaem, chto gazovye tumannosti polnost'yu prozrachny dlya izlucheniya v liniyah subordinatnyh serii i neprozrachny dlya izlucheniya v liniyah osnovnoi serii. Polagaya v uravneniyah (1) β_ik=1 (i = 2,3,4,...), β_1k=0 i prenebregaya ionizaciei iz vozbuzhdennyh sostoyanii, poluchaem

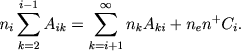
$\begin{eqnarray} n_{i} \sum_{k=2}^{i-1} A_{ik} = \sum_{k=i+1}^{\infty} n_{k} A_{ki}+ n_{e} n^{+}C_{i}.\nonumber \end{eqnarray}$ (12)

Sistema uravnenii (12) byla ran'she rassmotrena Cillie[1].

<< Glava I. Odnorodnaya sreda | Oglavlenie | 1.2 Stepen' vozbuzhdeniya i ionizacii >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce