Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 1.3 Otnositel'nye intensivnosti linii | Oglavlenie | 1.5 Sravnenie s nablyudeniyami >>

1.4 O prozrachnosti sredy dlya izlucheniya v liniyah

Kak bylo vyyasneno, s uvelicheniem parametra h stepen' vozbuzhdeniya bystro ubyvaet, i pri dostatochno bol'shih znacheniyah h sreda stanovitsya prozrachnoi dlya izlucheniya v liniyah vseh serii, nachinaya c j+1-i. Usloviem neprozrachnosti sredy v liniyah j-i serii yavlyaetsya vypolnenie neravenstva β_jk < 1. Odnako zaranee my ne mozhem skazat', nachinaya s kakoi serii sreda budet prozrachnoi, tak kak velichiny β_jk zavisyat ot velichin n_j yavlyayushihsya neizvestnymi. Zhelatel'no poetomu imet' prostoi sposob ocenki chisel n_j.

Seichas my dadim priblizhennyi metod resheniya sistemy (9), osnovannyi na tom obstoyatel'stve, chto pri bol'shih znacheniyah h chisla n_j bystro ubyvayut s vozrastaniem nomera j.

Skladyvaya pochlenno vse uravneniya (9), nachinaya s j-go, poluchaem

$\begin{eqnarray} \sum_{i=j}^{\infty} n_i\left[x\sum_{k=1}^{j-1} \frac{\frac{g_2}{g_1}n_1-n_2}{\frac{g_i}{g_k}n_k-n_i}\left(\frac{\nu_{ki}}{\nu_{12}}\right)^3+\frac{B_{ic}\rho_{ic}^*}{A_{21}}\right]=\frac{n_e n^+}{WA_{21}}\sum_{i=j}^{\infty} C_i,\nonumber \end{eqnarray}$ (21)

Prenebregaya einshteinovskim otricatel'nym poglosheniem i oboznachaya

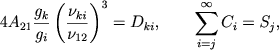
$\begin{eqnarray} 4A_{21}\frac{g_k}{g_i}\left(\frac{\nu_{ki}}{\nu_{12}}\right)^3=D_{ki}, \qquad \sum_{i=j}^{\infty} C_i=S_j,\nonumber \end{eqnarray}$ (22)

vmesto (21) nahodim

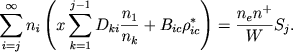
$\begin{eqnarray} \sum_{i=j}^{\infty} n_i\left(x\sum_{k=1}^{j-1} D_{ki}\frac{n_1}{n_k}+B_{ic}\rho_{ic}^*\right)=\frac{n_e n^+}{W}S_j.\nonumber \end{eqnarray}$ (23)

Prinimaya vo vnimanie ubyvanie chisel n_i i D_ki s vozrastaniem i, ogranichimsya v summirovanii po i odnim pervym chlenom. Togda poluchaem

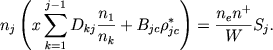
$\begin{eqnarray} n_j\left(x\sum_{k=1}^{j-1} D_{kj}\frac{n_1}{n_k}+B_{jc}\rho_{jc}^*\right)=\frac{n_e n^+}{W}S_j.\nonumber \end{eqnarray}$ (24)

My prishli k rekurentnoi formule, dayushei chislo n_j, esli izvestny chisla n₁, n₂,... n_j-1.

Dlya j=1 my mozhem vzyat' bolee tochnuyu formulu, chem ta, kotoraya sleduet iz (24), a imenno:

$\begin{eqnarray} n_1B_{ic}\rho_{ic}^* + n_2B_{2c}\rho_{2c}^*=\frac{n_e n^+}{W}S_1.\nonumber \end{eqnarray}$ (25)

Togda uravnenie (25) i vtoroe iz uravnenii (24) dayut

$\frac{n_2}{n_1}=\frac{(1-p)B_{ic}\rho_{ic}^*}{xA_{21}+pB_{2c}\rho_{2c}^*}$ (26)

gde $p=\frac{C_1}{S_1}$ . Privlekaya sleduyushee iz uravnenii (24), poluchaem

$\begin{eqnarray} \frac{n_3}{n_1} = \frac{S_3}{S_2}\frac{xA_{21}+B_{2c}\rho_{2c}^*}{xD_{13}+xD_{23}\frac{n_1}{n_2} + B_{3c}\rho_{3c}^*}\cdot\frac{n_2}{n_1}.\nonumber \end{eqnarray}$ (27)

I tak dalee.

Esli pri vychislenii po formulam (24) my poluchim takoe chislo n_j, chto okazhetsya β_jk > 1, to eto budet oznachat', chto sreda prozrachna dlya izlucheniya v j-i serii. Dopustim, chto my poluchili β_3k > 1, no β_2k < 1 . Eto znachit, chto sreda neprozrachna dlya izlucheniya v bal'merovskoi serii, no prozrachna dlya izlucheniya v posleduyushih seriyah. Vspominaya sootnoshenie (8), my nahodim, chto v etom sluchae dolzhno byt'

$\begin{eqnarray} \frac{A_{43}}{D_{34}}\cdot\frac{n_3}{n_1}<\beta_{12}<\frac{A_{32}}{D_{23}}\cdot\frac{n_2}{n_1},\nonumber \end{eqnarray}$ (28)

ili

$\begin{eqnarray} 30\frac{n_3}{n_1}<\beta_{12}<8\frac{n_2}{n_1}.\nonumber \end{eqnarray}$ (29)

Vychislyaya dlya primera otnosheniya $\frac{n_2}{n_1}$ i $\frac{n_3}{n_1}$ po formulam (26) i (27) pri T=20000^o, poluchaem, chto pri x=1,0 dolzhno byt'

$\begin{eqnarray} 2\cdot 10^{-4} < \beta_{12}<3\cdot 10^{-3},\nonumber \end{eqnarray}$ (30)

a pri x=10

$\begin{eqnarray} 2\cdot 10^{-6} < \beta_{12}<3\cdot 10^{-4}.\nonumber \end{eqnarray}$ (31)

Takovy usloviya, kotorye dolzhny vypolnyat'sya, esli sreda neprozrachna dlya izlucheniya v laimanovskoi i bal'merovskoi seriyah i prozrachna dlya izlucheniya v drugih seriyah. Predstavlyaet interes nahozhdenie bal'merovskogo dekrementa dlya tol'ko chto rassmotrennogo sluchaya. Pri vypolnenii poslednih uslovii my dolzhny polozhit' β_jk=1 (j=3, 4, 5,...). Togda sistema uravnenii (9) privoditsya k vidu:

$\begin{eqnarray} \left. \begin{array}{l} n_1B_{1c}W\rho_{1c}^* = \beta_{12}\sum\limits_{k=2}^{\infty} n_k D_{1k} + n_e n^+ C_1 \nonumber \\ \\ n_2(A_{21}\beta_{12} + B_{2c}W\rho_{2c}^*) = \frac{n_1}{n_2} \beta_{12}\sum\limits_{k=3}^{\infty} n_k D_{2k} + n_e n^+ C_2 \nonumber \\ \\ n_i\left[ \beta_{12}\left( D_{1i} + \frac{n_1}{n_2} D_{2i}\right) + \sum\limits_{k=3}^{i-1} A_{ik}+B_{ic}W\rho_{ic}^* \right]= \nonumber \\ \\ = \sum\limits_{k=i+1}^{\infty} n_k A_{ki} + n_e n^+ C_i \quad (i=3,4,5,...)\nonumber \end{array} \right\} \end{eqnarray}$ (32)

Sistema uravnenii (32) byla reshena nami chislenno dlya sleduyushih dvuh sluchaev:

T=20000^o, β₁₂=10^-3, W=10^-3, x=1.0,
T=20000^o, β₁₂=10^-5, W=10^-6, x=10.

Bal'merovskii dekrement, poluchennyi v rezul'tate resheniya, priveden v tabl. VII.

Tablica VII
Bal'merovskii dekrement pri β_jk=1 (j=3,4,5,..)

I II

H_α 2.0 8.9

H_β 1.00 1.00

H_γ 0.80 0.91

H_δ 0.61 0.84

Iz tablicy vidno, chto intensivnosti linii H_β, H_γ i H_δ blizki drug k drugu, no otnoshenie intensivnostei $\frac{H_{\alpha}}{H_{\beta}}$ ves'ma veliko. Etot bal'merovskii dekrement rezko otlichaetsya ot poluchennogo ranee (cm. tablicy IV i V). Na samom dele iz-za neodnorodnosti obolochek vozmozhny kombinacii oboih bal'merovskih dekrementov.

V sleduyushem paragrafe my uvidim, chto bal'merovskii dekrement ukazannogo v tabl. VII tipa deistvitel'no osushestvlyaetsya v nekotoryh obolochkah.

<< 1.3 Otnositel'nye intensivnosti linii | Oglavlenie | 1.5 Sravnenie s nablyudeniyami >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce