Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << Glava II. Zvezdy rannih klassov s yarkimi liniyami | Oglavlenie | 2.2 Izmenenie vozbuzhdeniya vdol' radiusa >>

2.1 Nizhnyaya granica atmosfery

Chtoby primenit' ranee poluchennye rezul'taty k zvezdnoi atmosfere, nado zadat' raspredelenie plotnoctei i skorostei v atmosfere. V dvuh pervyh paragrafah etoi glavy my rassmotrim atmosferu, obrazovannuyu materiei, vybrasyvaemoi iz zvezdy s postoyannoi skorost'yu. Togda plotnost' materii budet obratno proporcional'na kvadratu radiusa. Rassmotrenie takoi modeli yavlyaetsya naibolee prostym primerom primeneniya nashego metoda, v izlozhenii kotorogo i sostoit, sobstvenno govorya, nasha blizhaishaya cel'. S drugoi storony, takaya model' ves'ma blizko sootvetstvuet atmosferam zvezd tipov WR i R Cygni, a takzhe, v men'shei mere, atmosferam zvezd tipa Be. Poetomu rezul'taty, poluchennye putem rassmotreniya etoi modeli, budut dostatochno nadezhno harakterizovat' (po krainei mere v kachestvennom otnoshenii) atmosfery ukazannyh zvezd.

Opredelim snachala nizhnyuyu granicu zvezdnoi atmosfery. Dlya etogo neobhodimo znat', chem vyzyvaetsya pogloshenie v nepreryvnom spektre v verhnih sloyah zvezdy. Legko dokazat', chto dlya rassmatrivaemyh zvezd eto pogloshenie vyzyvaetsya ne fotoionizaciei i giperbolicheskimi perehodami, a rasseyaniem sveta svobodnymi elektronami. Esli eto tak, to radius nizhnei granicy atmosfery r₀ opredelyaetsya sootnosheniem

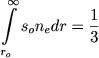
$\int\limits_{r_o}^{\infty}s_on_edr=\frac{1}{3}$ (1)

gde s₀ - rasseivayushaya sposobnost' svobodnogo elektrona.

My uzhe uslovilis' schitat', chto plotnost' v atmosfere padaet obratno proporcional'no kvadratu radiusa. Tak kak v atmosferah goryachih zvezd gromadnoe bol'shinstvo atomov. nahoditsya v ionizovannom sostoyanii, to my imeem

$n_e = n_e^o\left(\frac{r_o}{r}\right)^2,$ (2)

gde n_e⁰ - chislo svobodnyh elektronov na nizhnei granice atmosfery. Podstavlyaya (2) v (1), nahodim

$n_e^or_o = 0,5 \cdot 10^{24}$ (3)

Takova svyaz' mezhdu velichinami r₀ i n_e⁰, esli rasseyanie sveta svobodnymi elektronami igraet osnovnuyu rol' v pogloshenii v nepreryvnom spektre v naruzhnyh chastyah zvezdy.

Kak uzhe skazano, poslednee utverzhdenie legko dokazat'. Dlya etogo naidem opticheskuyu tolshinu atmosfery za granicei serii Laimana. My imeem

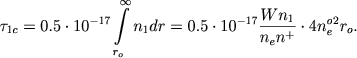
$\tau_{1c}=0.5 \cdot 10^{-17}\int\limits_{r_o}^{\infty}n_1dr=0.5 \cdot 10^{-17}\frac{Wn_1}{n_en^+} \cdot {4n_e^o}^2r_o.$ (4)

Esli prinyat', chto radius zvezdy v 10 raz bol'she radiusa Solnca (r₀=7 ⋅ 10¹¹), to iz (3) nahodim n_e⁰=7 ⋅ 10¹¹. S etimi znacheniyami (r₀ i n_e⁰) iz (4) poluchaem τ_1c < 1 , esli T_∗=20000°; . Pri takih malyh znacheniyah velichiny τ_1c opticheskaya tolshina atmosfery v vidimoi chasti spektra, obuslovlennaya fotoionizaciei i giperbolicheskimi perehodami, budet poryadka 0,001. Etim dokazyvaetsya spravedlivost' opredeleniya radiusa nizhnei granicy atmosfery formuloi (1).

Pri poluchenii sootnosheniya (4) my schitali, chto v atmosfere zvezdy spravedliva obychnaya ionizacionnaya formula

$n_e\frac{n^+}{n_1} = Wf(T_*),$ (5)

$f(T_*) = \frac{(2\pi mkT_*)^{\frac{3}{2}}}{h^3}e^{-\frac{h\nu_{1c}}{kT_*}} ;$ (6)

$W=\frac{1}{4}\left(\frac{r_o}{r}\right)^2.$ (7)

Tak kak dlya goryachih zvezd τ_1c < 1, to spravedlivost' etoi formuly ne vyzyvaet somnenii. V protivnom sluchae neobhodimo bylo by uchityvat' oslablenie izlucheniya, idushego ot zvezdy, vsledstvie ekstinkcii, i nalichie diffuznogo izlucheniya atmosfery za granicei laimanovskoi serii.

V dal'neishem my vezde budem schitat', chto τ_1c < 1. Vsledstvie etogo budet ne tol'ko vypolnyat'sya ionizacionnaya formula (5), no budut takzhe spravedlivymi chislennye rezul'taty predydushei glavy, pri poluchenii kotoryh prinimalos', chto ionizaciya vyzyvaetsya izlucheniem, idushim neposredstvenno ot zvezdy.

Legko poluchit' takzhe vtoroe sootnoshenie mezhdu velichinami r₀ i n_e⁰. Dlya etogo nado opredelit' kolichestvo energii, izluchaemoi atmosferoi v kakoi-libo spektral'noi linii. Imeya v vidu ispol'zovanie chislennyh rezul'tatov, poluchennyh nami ranee dlya vodorodnogo atoma, my v etoi glave budem govorit' lish' ob izluchenii atmosfery v bal'merovskih liniyah. Odnako nado zametit', chto podobnye raschety legko provesti dlya lyubogo atoma. Pust' H_k - polnaya energiya, izluchaemaya atmosferoi v k-i linii bal'merovskoi serii. My imeem

$H_k=\int n_k A_{k2}h\nu_{2k}\beta_{2k}dV,$ (8)

gde β_2k - dolya kvantov, uhodyashih iz atmosfery, vsledstvie effekta Doplera, i integrirovanie rasprostraneno po vsemu ob'emu atmosfery. Eta formula mozhet byt' preobrazovana k vidu

$H_k=\frac{16}{k^2}\left(\frac{\nu_{2k}}{\nu_{12}}\right)^3 A_{21}h\nu_{2k}\int f_k n_e n^+ dV ,$ (9)

gde

$f_k = \frac{n_k}{n_2} \frac{1-\frac{g_1}{g_2}\frac{n_2}{n_1}}{1-\frac{g_2}{g_k}\frac{n_k}{n_2}} \frac{Wn_1}{n_e n^+}x\approx \frac{n_k}{n_2} \frac{Wn_1}{n_e n^+}x.$ (10)

No velichina f_k slabo zavisit ot parametra x. Naprimer, pri T=20000°; my imeem:

x 0.01 0.1 1.0

10²⁰f₄ 0.11 0.19 0.12

Poetomu velichinu f_k mozhno vynesti za znak integrala. Schitaya, chto n_e=n⁺, vmesto (9) poluchaem

$H_k = \frac{64\pi}{k^2}\left(\frac{\nu_{2k}}{\nu_{12}}\right)^3 A_{21}h\nu_{2k} f_k {n_e^o}^2 r_o^3 .$ (11)

Eto est' okonchatel'naya formula, opredelyayushaya velichinu N_k.

S drugoi storony, velichinu N_k mozhno vyrazit' cherez zanstrovskuyu velichinu A_k, poluchaemuyu iz sravneniya intensivnosti linii i intensivnosti sosednego uchastka nepreryvnogo spektra zvezdy,

$H_k = A_k\frac{8\pi^2 r_o^2 h\nu_2 k^4}{c^2}\frac{1}{e^{\frac{h\nu_{2k}}{kT}}-1}.$ (12)

Dve poslednie formuly dayut

$\frac{8}{k^2} A_{21} f_k {n_e^o}^2 r_o = A_k\frac{\pi}{c^2} \frac{{\nu_{12}}^3}{e^{\frac{h\nu_{2k}}{kT}}-1}.$ (13)

My poluchili novoe sootnoshenie [naryadu s sootnosheniem (3)], svyazyvayushee velichiny r₀ i n_e⁰. Sootnosheniya (3) i (13) dayut vozmozhnost' opredeleniya velichin r₀ i n_e⁰, t. e. radiusa nizhnei granicy atmosfery i elektronnoi plotnosti na etoi granice. Vo vtoroe iz etih sootnoshenii, krome velichin r₀ i n_e⁰, vhodyat zanstrovskaya velichina A_k, poluchaemaya iz nablyudenii, i temperatura zvezdy. My budem schitat' temperaturu zvezdy izvestnoi i dlya primera rassmotrim dva sluchaya: 1) T = 20000°; (zvezdy tipov R Cygni i Be) i 2) T=50000°; (zvezdy tipa WR).

V pervom iz etih sluchaev my mozhem vzyat': f₄ = 0,15 ⋅ 10^-20, A₄ = 0,004 (srednee dlya mnogih zvezd tipa Be, po Mohler [1]), a vo vtorom: f₄ = 0,4 ⋅ 10^-21, A₄ = 0,002 (dlya zvezdy HD 192163, po dannym Beals). Sootnosheniya (3) i (13) dlya nashih dvuh sluchaev dayut: 1) n_e⁰ = 3,6 ⋅ 10¹¹, r₀ = 1,4 ⋅ 10¹² = 20r_☉. 2) n_e⁰ = 1,5 ⋅ 10¹², r₀ = 3,3 ⋅ 10¹¹ = 5r_☉.

Poluchennye znacheniya velichin r₀ i n_e⁰ predstavlyayutsya nam ves'ma pravdopodobnymi. Dlya sravneniya mozhno, naprimer, otmetit', chto dlya dvuh zatmennyh peremennyh zvezd. tipa WR byli polucheny sleduyushie znacheniya radiusa: r₀ = 5,8r_☉ i r₀ = 5,5r_☉ (sm. stat'yu Gaposchkin [2]).

Pol'zuyas' naidennymi znacheniyami r₀ i n_e⁰, mozhno, mezhdu prochim, podschitat' kolichestvo materii, vybrasyvaemoe zvezdoi za god. Vybrasyvaemaya massa, ochevidno, ravna

$M=4\pi {r_0}^2 n_e^0 m_H v \cdot 3,16 \cdot 10^7,$ (14)

gde m_H - massa vodorodnogo atoma i v - skorost' istecheniya materii. Eta formula daet: M ≈ 10^-5M_☉ dlya zvezd tipov WR i P Cygni i M ≈ 10^-6M_☉ - dlya zvezd tipa Be.

Nado zametit', chto primenenie poluchennyh formul ogranichivaetsya nenadezhnost'yu imeyushihsya znachenii zvezdnyh temperatur. Kak izvestno, temperatury zvezd tipa WR, opredelyaemye metodom Zanstra, okazyvayutsya tem bolee vysokimi, chem vyshe potencial ionizacii togo elementa, po liniyam kotorogo temperatura opredelyaetsya. Tak, naprimer, temperatury, opredelennye po liniyam vodoroda, ionizovannogo geliya i chetyre raza ionizovannogo kisloroda, okazyvayutsya poryadka 20000°; , 60000°; i 100000°; sootvetstvenno. V znachitel'noi mere eto rashozhdenie vyzyvaetsya sil'nym otkloneniem izlucheniya zvezdy ot izlucheniya absolyutno chernogo tela, chto v obshih chertah ob'yasnyaetsya teoriei protyazhennyh fotosfer. Mozhno ukazat' takzhe ryad drugih faktorov, skazyvayushihsya na opredelenii temperatur metodom Zanstra. Odin iz etih faktorov sostoit v tom, chto pri vysokoi temperature zvezdy opticheskaya tolshina atmosfery za granicei osnovnoi serii atoma s sravnitel'no nizkim potencialom ionizacii dolzhna byt' men'she edinicy. Vsledstvie etogo atmosfera budet pogloshat' lish' nebol'shuyu chast' izlucheniya zvezdy za granicei osnovnoi serii dannogo atoma, i temperatura, opredelennaya po liniyam etogo atoma, okazhetsya zanizhennoi. Kak vidno iz formuly (4), tak obstoit delo s vodorodom, esli temperatura zvezdy bol'she 20000°; . Dlya etogo sluchaya s pomosh'yu formuly (4) metod Zanstra legko utochnit'. Dlya etogo levuyu chast' uravneniya Zanstra [sm. uravnenie (60) sleduyushei glavy] nado umnozhit' na velichinu τ_1c, vzyatuyu iz formuly (4). Odnako poluchennoe takim obrazom sootnoshenie budet slabo zaviset' ot temperatury zvezdy, ibo s rostom temperatury uvelichivaetsya chislo kvantov za granicei osnovnoi serii, no padaet velichina τ_1c. Krome togo, v eto sootnoshenie voidet novaya neizvestnaya velichina - radius zvezdy r₀ [velichina n_e⁰ mozhet byt' isklyuchena s pomosh'yu (3)]. Bolee tochnaya svyaz' takogo zhe tipa mezhdu T_∗ i r₀ (s uchetom neprozrachnosti atmosfery dlya izlucheniya v liniyah i poglosheniya za granicami subordinatnyh serii) osushestvlyaetsya vysheprivedennoi formuloi (13).

<< Glava II. Zvezdy rannih klassov s yarkimi liniyami | Oglavlenie | 2.2 Izmenenie vozbuzhdeniya vdol' radiusa >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce