Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu Dvizhushiesya obolochki zvezd << 2.1 Nizhnyaya granica atmosfery | Oglavlenie | 2.3 Kontury spektral'nyh linii >>

2.2 Izmenenie vozbuzhdeniya vdol' radiusa

Kak bylo vyyasneno v predydushei glave, stepen' vozbuzhdeniya atomov v dvizhusheisya atmosfere zavisit ot dvuh parametrov: ot temperatury zvezdy T∗ i ot parametra h. Dlya parametra h my imeem

$$ x=\frac{1}{2un_1 x_{12} W} \frac{\overline{dv}}{ds}, $$ (15)

gde u - srednyaya termicheskaya skorost' atomov, x12 - srednii koefficient poglosheniya v spektral'noi linii, rasschitannyi na odin atom, i $\frac{\overline{dv}}{ds}$ - usrednennyi po napravleniyam gradient skorosti. Chtoby naiti, kak menyaetsya stepen' vozbuzhdeniya vdol' radiusa, nam nado predstavit' parametr x v vide funkcii ot r.

Legko videt', chto v atmosfere, obrazovannoi vybrasyvaemoi iz zvezdy materiei, gradient skorosti raven

$$ \frac{dv}{ds} = \frac{dv}{dr} \cos^2\theta+\frac{v}{r}\sin^2\theta, $$ (16)

gde $\frac{dv}{dr}$ - gradient skorosti vdol' radiusa i θ - ugol mezhdu dannymi napravleniyami i radiusom-vektorom. Esli skorost' istecheniya postoyannaya. to

$$ \frac{\overline{dv}}{ds} = \frac{2}{3} \frac{v}{r}. $$ (17)

Usityvaya (17), (5) i (2), vmesto (15) nahodim

$$ x = x_0 \left(\frac{r}{r_0}\right)^3, $$ (18)

gde

$$ x_0 = \frac{v f(T_*)}{3ux_{12} r_0 {n_e^0}^2} . $$ (19)

Tak kak ne0r0 = 0,5 ⋅ 1024, a dlya linii Lα i x12 = 6,8 ⋅ 10-8, to dlya vodoroda

$$ x_0 = 10^{-17} \frac{vf(T_*)}{n_e^0} . $$ (20)

Pri v = 100 km/sek, dlya dvuh rassmotrennyh vyshe sluchaev (T=20000°; i T=50000°; ) eto daet h0=0,001 i h0=0,1.

My vidim, chto v sluchae istecheniya materii s postoyannoi skorost'yu parametr h vozrastaet proporcional'no kubu radiusa. Sledovatel'no, v etom sluchae stepen' vozbuzhdeniya ves'ma bystro ubyvaet s uvelicheniem radiusa. Chtoby predstavit' stepen' vozbuzhdeniya v vide funkcii ot r, nado vychislit' h po formule (18) i zatem vospol'zovat'sya tablicami 2 i 3 predydushei glavy. Zametim, chto takoe predstavlenie budet vernym tol'ko vo vnutrennih chastyah atmosfery. Vo vneshnih zhe chastyah atmosfery, gde atmosfera prozrachna dlya izlucheniya v liniyah subordinatnyh serii, velichiny $\frac{n_i}{n_1}$ budut prosto proporcional'ny $\frac{n_i n^+}{n_1}$ t.e. stepen' vozbuzhdeniya budet ubyvat' kak $\frac{1}{r^2}$.

Predstavlyaet interes nahozhdenie granicy mezhdu neprozrachnoi i prozrachnoi chastyami atmosfery, t.e., inache govorya, verhnei granicy obrashayushego sloya. Tak kak eta granica razlichna dlya raznyh linii, to dlya opredelennosti my naidem ee dlya linii Nα, opredelyaya ee sootnosheniem

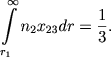
$$ \int\limits_{r_{1}}^{\infty} n_2 x_{23} dr = \frac{1}{3} . $$ (21)

Dlya bol'shih znachenii x my priblizhenno imeem

$$ \frac{n_2}{n_1} = (1-p) \frac{B_{1c} \rho_{1c}^*}{xA_{21}} , $$ (22)

[sm. formulu (25) predydushei glavy] i, ispol'zuya (5), (18) i (21), poluchaem

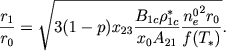
$$ \frac{r_1}{r_0} = \sqrt{3(1-p) x_{23} \frac{B_{1c} \rho_{1c}^*}{x_0 A_{21}} \frac{{n_e^0}^2 r_0}{f(T_*)}} . $$ (23)

Dlya dvuh sluchaev, rassmotrennyh vyshe, formula (23) daet $\frac{r_1}{r_0}=12$ i $\frac{r_1}{r_0}=4$. Takim obrazom my vidim, chto rassmatrivaemye zvezdy obladayut ves'ma protyazhennym obrashayushim sloem. Etot vyvod, mezhdu prochim, dolzhen imet' znachenie pri vychislenii konturov linii poglosheniya, obrazovannyh atmosferami etih zvezd.

S voprosom ob izmenenii stepeni vozbuzhdeniya vdol' radiusa tesno svyazan vopros o kolichestve energii, izluchaemoi raznymi sloyami atmosfery. Esli stepen' vozbuzhdeniya kak funkciya ot radiusa izvestna, to etot vopros reshaetsya s pomosh'yu formul (8) i (9) (v kotoryh, odnako, integrirovat' nado ne po vsemu ob'emu atmosfery, a tol'ko po interesuyushemu sloyu). Pri takogo roda vychisleniyah vyyasnyayutsya sleduyushie vazhnye obstoyatel'stva:

  1. Pust' Hk0 i Hk' sut' kolichestva energii, izluchaemoi v k-i linii bal'merovskoi serii sootvetstvenno obrashayushim sloem i prozrachnoi chast'yu atmosfery. My, ochevidno, imeem

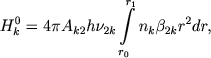
    $$ H_k^0 = 4\pi A_{k2} h\nu_{2k} \int\limits_{r_0}^{r_1} n_k \beta_{2k} r^2 dr , $$ (24)

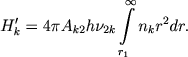
    $$ H_k^{\prime} = 4\pi A_{k2} h\nu_{2k} \int\limits_{r_1}^{\infty} n_k r^2 dr . $$ (25)

    Vychislenie etih integralov pokazyvaet, chto osnovnuyu chast' energii izluchaet ne prozrachnaya chast' atmosfery, a obrashayushii sloi. Tak, naprimer, v pervom iz nashih sluchaev (T=20000°;) dolya energii, izluchaemoi prozrachnoi chast'yu atmosfery, sostavlyaet tol'ko okolo 20%. Etot vyvod protivorechit obsheprinyatomu mneniyu i dokazyvaet pravil'nost' nashei tochki zreniya.

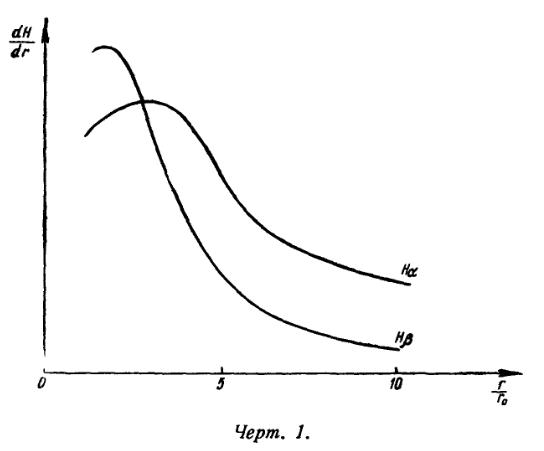
  2. Pust' 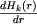$\frac{dH_k(r)}{dr}$ est' kolichestvo energii, izluchaemoi v k-i bal'merovskoi linii sfericheskim sloem edinichnoi tolshiny, nahodyashimsya na rasstoyanii r ot centra zvezdy. Vychisleniya pokazyvayut, chto dlya raznyh linii eta velichina dostigaet maksimuma v raznyh mestah. Dlya primera my vychislili etu velichinu dlya linii Hα i Hβ (pri T=20000°; ). Rezul'taty vychislenii v uslovnyh edinicah predstavleny na chert. 1.

    Iz chertezha vidno, chto osnovnaya chast' energii v linii Hβ izluchaetsya bolee glubokimi sloyami, chem v linii Hα. Naprimer, polovina energii v linii Hβ izluchaetsya vnutri sfery radiusa r = 3r0, a polovina energii v linii Hα - vnutri sfery radiusa r = 6r0. Etot vyvod vazhen dlya ob'yasneniya otmechennoi nablyudatelyami stratifikacii vodorodnogo izlucheniya v protyazhennyh atmosferah (sm., naprimer, stat'yu

    Goedicke o zvezde W Cephei [3] i stat'yu Baldwin o zvezde γ Cassiopeiae [4]).

    V zaklyuchenie zametim, chto, hotya izlozhennye vyshe rezul'taty polucheny dlya vpolne opredelennoi modeli atmosfery (skorost' istecheniya materii postoyanna, plotnost' ubyvaet obratno proporcional'no kvadratu radiusa), odnako, nesomnenno, chto v obshih chertah oni spravedlivy dlya vseh goryachih sverhgigantov. Chtoby prodelat' podobnoe issledovanie dlya konkretnoi zvezdy, neobhodimo znat' raspredelenie plotnostei i skorostei v ee atmosfere. Vazhnyi vopros o tom, kak poluchit' eti dannye iz nablyudenii, mozhet byt' reshen putem sravneniya nablyudennyh i teoreticheskih konturov spektral'nyh linii. Probleme teoreticheskogo opredeleniya konturov linii, obrazovannyh dvizhushimisya atmosferami, posvyashaetsya sleduyushii paragraf.

    << 2.1 Nizhnyaya granica atmosfery | Oglavlenie | 2.3 Kontury spektral'nyh linii >>
Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya
Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe:

Obsudit' etu publikaciyu
Ocenka: 2.9 [golosov: 138]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya