Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 2.2 Izmenenie vozbuzhdeniya vdol' radiusa | Oglavlenie | Glava III. Gazovye tumannosti >>

2.3 Kontury spektral'nyh linii

Vopros o konturah spektral'nyh linii, obrazovannyh dvizhushimisya atmosferami zvezd, rassmatrivalsya v rabotah mnogih avtorov. Vo vseh etih rabotah predpolagalos', chto temnye komponenty yarkih linii voznikayut v obrashayushem sloe, nahodyashemsya nizhe prozrachnoi obolochki, v kotoroi obrazuyutsya yarkie linii. Odnako v predydushem paragrafe bylo pokazano, chto takoi vzglyad yavlyaetsya nepravil'nym. Na samom dele kak temnye, tak i yarkie linii voznikayut v odnom i tom zhe protyazhennom obrashayushem sloe. Poetomu neobhodimo dat' teoriyu konturov spektral'nyh linii, osnovannuyu na etoi novoi tochke zreniya.

Voobshe govorya, vopros o nahozhdenii konturov linii dlya dvizhushihsya obolochek yavlyaetsya gorazdo bolee slozhnym chem dlya nepodvizhnyh. Odnako v tom predel'nom sluchae, kogda skorost' dvizheniya obolochki znachitel'no prevoshodit srednyuyu termicheskuyu skorost' atomov, kontury linii mogut byt' vychisleny ves'ma legko. Eto proishodit ottogo, chto v etom sluchae mozhno prenebrech' vsemi faktorami, vliyayushimi na kontur linii, krome odnogo - dvizheniya obolochki. I tol'ko v etom sluchae mozhet byt' dostatochno uverenno reshena i obratnaya zadacha - nahozhdenie po konturam linii parametrov, opredelyayushih dvizhenie obolochki. Mozhno schitat', chto ukazannyi sluchai v ochen' horoshem priblizhenii osushestvlyaetsya v obolochkah zvezd tipov WR, P Cygni, Be i Novyh. Imenno etot sluchai my i rassmatrivaem v nastoyashem paragrafe.

Dlya prostoty my schitaem, chto imeetsya rezkaya granica mezhdu fotosferoi i atmosferoi zvezdy. V otlichie ot obychnoi terminologii pod liniei poglosheniya my ponimaem liniyu, obrazovannuyu poglosheniem sveta, idushego ot fotosfery, v atmosfere zvezdy, a pod liniei izlucheniya - liniyu, obrazovannuyu izlucheniem sveta samoi atmosferoi (s uchetom samoobrasheniya). Nalozhenie vtoroi linii na pervuyu daet nablyudaemuyu spektral'nuyu liniyu.

Yasno, chto vychislenie konturov linii poglosheniya (v nashem smysle) ne vyzyvaet zatrudnenii. Dlya etogo dlya kazhdoi chastoty ν nado naiti sootvetstvuyushuyu poverhnost' ravnyh luchevyh skorostei. Chast' etoi poverhnosti, nahodyashayasya v obrashayushem sloe, zakryvaet ot nablyudatelya nekotoruyu chast' diska zvezdy. Ostavshayasya otkrytoi chast' diska zvezdy daet ostatochnuyu intensivnost' linii poglosheniya v chastote ν.

Chtoby vychislit' kontur linii izlucheniya, nado dlya kazhdoi chastoty naiti yarkost' sootvetstvuyushei poverhnosti ravnyh luchevyh skorostei (ibo v otlichie ot sluchaya prozrachnoi obolochki, kogda izluchaet ob'em, v sluchae neprozrachnoi obolochki, grubo govorya, izluchaet poverhnost'). Dlya etogo neobhodimo opredelit' intensivnost' izlucheniya, vyhodyashego (vsledstvie effekta Doplera) iz kazhdogo mesta atmosfery. Oboznachaya cherez J_ik(r) intensivnost' izlucheniya, sootvetstvuyushego perehodu k → i, vyhodyashego iz atmosfery na rasstoyanii r ot centra zvezdy, my, ochevidno, imeem

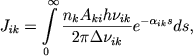
$J_{ik} = \int\limits_0^\infty \frac{n_k A_{ki} h\nu_{ik}}{2\pi\Delta\nu_{ik}} e^{-\alpha_{ik}s} ds,$ (26)

ili, proizvodya integrirovanie:

$J_{ik}(r) = \frac{2h{\nu_{ik}}^3}{c^2} \frac{1}{\frac{g_k}{g_i} \frac{n_i}{n_k}-1}.$ (27)

Velichiny $\frac{n_i}{n_k}$ v vide funkcii ot r dolzhna dat' teoriya luchevogo ravnovesiya dvizhusheisya sredy. V kachestve takoi teorii mozhno ispol'zovat' rezul'taty, poluchennye nami ranee.

Osnovyvayas' na izlozhennyh soobrazheniyah, my v etom, paragrafe vychislyaem kontury spektral'nyh linii otdel'no dlya dvuh sluchaev: a) dlya zvezd tipov WR, P Cygni i Novyh (t.e. dlya sluchaya istecheniya materii iz zvezd) i b) dlya zvezd, tipa Be (t.e. dlya sluchaya istecheniya materii iz bystro vrashayushihsya zvezd).

a)Zvezdy tipov WR, P Cygni i Novye

Kak izvestno, v spektrah Novyh do maksimuma bleska vidny absorbcionnye linii, sil'no smeshennye v fioletovuyu storonu, bez zametnyh sledov emissii. Posle maksimuma poyavlyayutsya yarkie linii, ogranichennye s fioletovoi storony absorbcionnymi sputnikami. Podobnyi zhe vid imeyut linii v spektrah zvezd tipov WR i R Cygni. Takoi harakter spektra govorit o nepreryvnom istechenii materii iz zvezd tipov WR i R Cygni i o vybrasyvanii obolochek pri vozgoranii Novyh. Dlya vyyasneniya vseh osobennostei dvizheniya materii, vybrasyvaemoi iz zvezd, neobhodim podrobnyi analiz konturov spektral'nyh linii.

V teoreticheskih rabotah drugih avtorov kontury vychislyalis' otdel'no dlya temnyh i dlya yarkih linii. Dlya polucheniya konturov absorbcionnyh linii, obrazovannyh dvizhusheisya atmosferoi, obychno bralis' kontury linii, obrazovannyh nepodvizhnoi atmosferoi, i opredelyalas' deformaciya etih konturov, proishodyashaya ottogo, chto raznye chasti atmosfery imeyut raznuyu skorost' po otnosheniyu k nablyudatelyu. Takovy raboty Carroll [5], Gerasimovicha i Mel'nikova [6], Wilson [7], Voroncova-Vel'yaminova [8] i dr., stavivshie svoei cel'yu ob'yasnenie konturov absorbcionnyh linii v spektrah Novyh pered maksimumom bleska. Odnako vse eti raboty imeyut tot nedostatok, chto v nih vse delo svoditsya k "nablyudaemomu" effektu Doplera, v to vremya kak v deistvitel'nosti neobhodimo vvesti effekt Doplera v uravneniya perenosa izlucheniya. Vpervye takaya popytka (tochnee govorya, popytka resheniya problemy Shustera pri uchete effekta Doplera), byla predprinyata Ms Sgea i Mitra [9]. Sovsem nedavno rassmotreniem etoi problemy zanimalsya Chandrasekhar [10]. Odnako v etih rabotah ne uchityvalos' izmenenie chastoty svetovogo kvanta, proishodyashee pri elementarnom akte rasseyaniya, vsledstvie effekta Dopplera, obuslovlennogo teplovym dvizheniem atomov. Kontury linii, vychislennye v perechislennyh rabotah, okazalis' malo pohozhimi na nablyudennye. Eto ob'yasnyaetsya ne tol'ko netochnost'yu ucheta dvizheniya obolochki, no takzhe tem, chto ne byla prinyata vo vnimanie bol'shaya protyazhennost' obrashayushego sloya, harakternaya dlya rassmatrivaemyh zvezd.

Pri nahozhdenii konturov emissionnyh linii v rabotah drugih avtorov predpolagalos', chto atmosfera zvezdy polnost'yu prozrachna dlya izlucheniya v liniyah. Vpervye etim voprosom zanimalsya Beals [11], pokazavshii, chto emissionnye linii, obrazovannye obolochkoi, sostoyashei iz atomov, dvizhushihsya s postoyannoi skorost'yu v radial'nom napravlenii, dolzhny imet' pryamougol'nye kontury. Odnako kontury emissionnyh linii v spektrah zvezd tipa WR i Novyh yavlyayutsya, kak pravilo, zakruglennymi. Vsledstvie etogo poyavilas' mysl', chto atomy, obrazuyushie obolochku, dvizhutsya ne s postoyannoi skorost'yu, a uskorenno ili zamedlenno. Kontury linii izlucheniya dlya etih sluchaev opredeleny v rabotah Gerasimovicha [12], Chandrasekhar [13] i Wilson [7] . Sovershenno ochevidno, chto pri podhodyashem vybore gradienta skorosti mozhno poluchit' lyuboi simmetrichnyi kontur.

Na samom dele, kak uzhe skazano, nado schitat', chto kak temnye, tak i yarkie linii voznikayut v odnom i tom zhe protyazhennom obrashayushem sloe. Pristupaya k nahozhdeniyu konturov linii, voznikayushih v takom sloe, my dlya prostoty dopustim, chto iz zvezdy proishodit istechenie materii so skorost'yu v, ne menyayusheisya s rasstoyaniem. Naidem snachala kontury linii poglosheniya (v nashem smysle).

Pust' r₀ i r₁ - sootvetstvenno nizhnyaya i verhnyaya granicy obrashayushego sloya. Atomy, dvizhushiesya v atmosfere pod uglom θ k nablyudatelyu, pogloshayut izluchenie, idushee ot fotosfery, chastota kotorogo ravna

$\nu = \nu_0 + \nu_0 \frac{v}{c} \cos\theta.$ (28)

Eti atomy ekraniruyut kol'ceobraznuyu chast' diska zvezdy, zaklyuchennuyu mezhdu uglami θ i θ₁, gde θ₁ opredelyaetsya usloviem:

$\left. \begin{array}{rrr} \sin\theta_1 = \frac{r_1}{r_0}\sin\theta, \qquad \mbox{esli} \qquad r_1\sin\theta < r_0 \\ \theta_1 = \frac{\pi}{2}, \qquad \mbox{esli} \qquad r_1\sin\theta > r_0 \end{array} \right\}$ (29)

Sledovatel'no, otnoshenie intensivnosti chastoty ν v spektral'noi linii k intensivnosti sosednego mesta v nepreryvnom spektre budet ravno

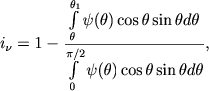
$i_{\nu} = 1-\frac{\int\limits_{\theta}^{\theta_1} \psi(\theta) \cos\theta\sin\theta d\theta}{\int\limits_0^{\pi/2} \psi(\theta) \cos\theta\sin\theta d\theta} ,$ (30)

gde ψ (θ) est' zakon potemneniya diska ot centra k krayu. Etoi formuloi i opredelyaetsya kontur linii poglosheniya.

Dlya funkcii ψ (θ) my ne mozhem vzyat' ee obychnoe vyrazhenie, tak kak rassmatrivaemye zvezdy obladayut protyazhennymi fotosferami, chto privodit k bolee sil'nomu potemneniyu diska pri perehode ot centra k krayu, chem dlya obychnyh zvezd. Poetomu funkciyu ψ (θ) my berem v vide

$\psi (\theta) = a + b\,{\cos}^n \theta ,$ (31)

gde a, b, n - nekotorye parametry.

Legko videt', chto nahozhdenie konturov linii poglosheniya dlya raznyh $\frac{r_1}{r_0}$ svoditsya k nahozhdeniyu konturov dlya r₁ = ∞ , t.e. dlya θ₁ = π/2. V poslednem zhe sluchae, podstavlyaya (31) v (30) i integriruya, my nahodim

$i_{\nu} = \frac{(n+2)a(1-y^2)+2b(1-y^{n+2})}{(n+2)a+2b} ,$ (32)

gde vmesto chastoty ν vvedena velichina y, svyazannaya s chastotoi sootnosheniem

$\frac{\bar \nu - \nu_0}{\nu_0} = \frac{v}{c}, \quad \nu = \nu_0 + y(\bar \nu - \nu_0).$ (33)

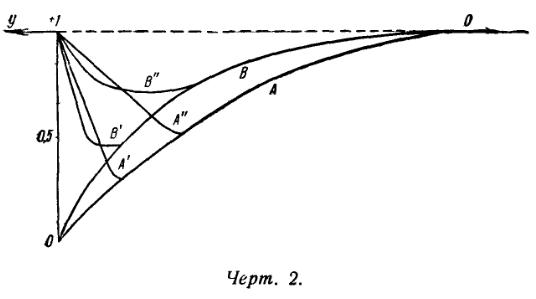
Kontury linii poglosheniya, vychislennye po vysheperechislennym formulam, dlya dvuh zakonov potemneniya:

$A)\, b=0, \qquad B)\,\frac{b}{a}=4, \; n=4 ,$ (34)

dany na chert. 2. Kontury, poluchennye dlya sluchaya r₁=∞ , oboznacheny bukvami A i B. Bukvami A'v, B' i A", B" otmecheny kontury, vychislyaemye dlya dvuh sleduyushih sluchaev: $\frac{r_1}{r_0}=2, \quad \frac{r_1}{r_0}=\sqrt{2}$ .

Pereidem teper' k nahozhdeniyu konturov linii izlucheniya. Dlya nahozhdeniya energii chastoty ν, izluchaemoi atmosferoi, nado prointegrirovat' intensivnost' izlucheniya, vyhodyashego iz atmosfery, po sootvetstvuyushei poverhnosti ravnyh luchevyh skorostei. V dannom sluchae eta poverhnost' yavlyaetsya konusom s vershinoi v centre zvezdy i os'yu, napravlennoi k nablyudatelyu. Poetomu dlya iskomoi energii my poluchaem

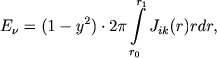
$E_{\nu} = (1-y^2)\cdot 2\pi \int\limits_{r_0}^{r_1} J_{ik}(r)rdr,$ (35)

gde intensivnost' J_ik(r) opredelyaetsya ravenstvom (27). Takim obrazom, v sluchae istecheniya materii s postoyannoi skorost'yu, kontur linii izlucheniya okazyvaetsya parabolicheskim (oboznachen bukvoi S na chert. 3).

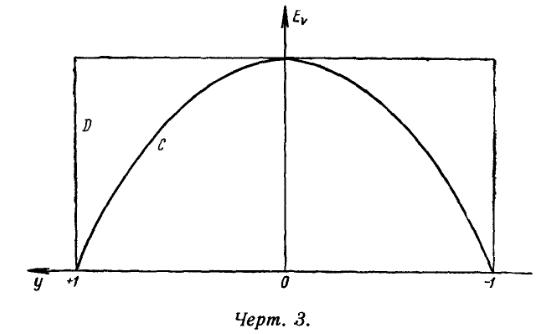
Chtoby poluchit' kontur spektral'noi linii, nado nalozhit' liniyu izlucheniya na liniyu poglosheniya (primery konturov kotoryh dany na chert. 2). Pri etom okazyvayutsya vozmozhnymi tri sluchaya [v zavisimosti glavnym obrazom ot znacheniya integrala v formule (35)]:

Voobshe govorya, poluchayutsya yarkie linii s temnymi komponentami na fioletovoi storone, t. e. linii takogo zhe, vida, kak v spektrah zvezd tipov R Cygni, WR i Novyh. Sleduet otmetit', chto parabolicheskii kontur yarkoi linii okazyvaetsya gorazdo blizhe k nablyudaemym, chem pryamougol'nyi kontur D, poluchennyi Beals dlya prozrachnyh obolochek.

Esli liniya poglosheniya slaba, a liniya izlucheniya, naoborot, sil'na, to vtoraya iz nih mozhet "zapolnit'" pervuyu, i my uvidim odnu tol'ko liniyu izlucheniya. Takoi sluchai chasto osushestvlyaetsya v spektrah zvezd tipa WR (pri etom igraet takzhe nekotoruyu rol' vliyanie izlucheniya prozrachnoi chasti obolochki, dayushego kontur tipa D). Imenno poetomu emissionnye linii v spektrah etih zvezd okazyvayutsya asimmetrichnymi i "smeshennymi" v krasnuyu storonu spektra. Dlya ob'yasneniya etogo "krasnogo smesheniya" Wilson [15] predpolozhil nalichie gravitacionnogo effekta. My vidim, odnako, chto v takoi gipoteze net neobhodimosti.

Esli liniya poglosheniya sil'na, a liniya izlucheniya, naoborot, slaba, to my uvidim odnu tol'ko liniyu poglosheniya (v obychnom smysle). Ostatochnaya intensivnost' v linii sozdaetsya pri etom ne svetom, rasseyannym atmosferoi, a fotosfernym izlucheniem, ne ekranirovannym dvizhushimisya atomami. Takoi sluchai imeet mesto v spektrah novyh zvezd pered maksimumom bleska. Kak izvestno, eti linii yavlyayutsya rezkimi i uzkimi (prichem shirina linii znachitel'no men'she ee smesheniya). Imenno takogo roda linii izobrazheny na chert. 2. Iz etogo chertezha vidno, chto liniya tem rezche, chem bol'she tolshina obrashayushego sloya, i tem uzhe, chem bol'she potemnenie diska ot centra k krayu. Otmetim, chto v rannih rabotah, posvyashennyh teoreticheskomu opredeleniyu konturov linii poglosheniya v spektrah novyh zvezd, prinimalos', chto tolshina obrashayushego sloya mala, a zakon potemneniya diska k krayu imeet obychnuyu formu. Vychislennye pri etih predpolozheniyah kontury poluchalis' shirokimi i neglubokimi. Vpervye na vazhnost' sil'nogo potemneniya diska k krayu obratil vnimanie B. A. Voroncov-Vel'yaminov [8], a na vazhnost' bol'shoi protyazhennosti obrashayushego sloya - E. R. Mustel' [14]. V deistvitel'nosti, kak my vidim, vazhny obe eti prichiny.

b) Zvezdy tipa Be
Kak pravilo, v spektrah zvezd tipa Be yarkie lini nakladyvayutsya na shirokie i neglubokie polosy poglosheniya. V svoyu ochered' na yarkie linii nakladyvayutsya uzkie linii poglosheniya, razdelyaya ih na dva komponenta. Odnako v nekotoryh spektrah yarkie linii yavlyayutsya odinochnymi, v drugih spektrah - kak odinochnymi, tak i dvoinymi.
Po-vidimomu, vse Ve-zvezdy yavlyayutsya "zvezdami s peremennymi spektrami". V odnih sluchayah proishodit izmenenie polnoi intensivnosti yarkih linii, a inogda ih poyavlenie i ischeznovenie (Pleiona, μ Centavra i dr.), v drugih - periodicheski menyaetsya otnoshenie intensivnostei dvuh komponentov kazhdoi emissionnoi linii (prichem inogda krasnyi komponent yarche, inogda fioletovyi). Dlya zvezd vtoroi gruppy (ih nazyvayut "zvezdami tipa φ Persei") zamecheny sleduyushie zakonomernosti. S izmeneniem intensivnostei komponentov svyazano izmenenie smesheniya linii. Kogda krasnyi komponent sil'nee, emissionnaya liniya i ee central'naya absorbciya smesheny v fioletovuyu storonu spektra. Kogda fioletovyi komponent sil'nee, eti linii smesheny v krasnuyu storonu spektra. Kogda emissionnye komponenty ne ravny, shirokaya polosa poglosheniya sil'nee vystupaet na storone bolee sil'nogo komponenta.
Dlya ob'yasneniya konturov linii v spektrah zvezd tipa Be Otto Struve [15] vyskazal gipotezu, soglasno kotoroi polosy poglosheniya obrazuyutsya v obrashayushem sloe bystro vrashayusheisya zvezdy, a razdvoennye yarkie linii - v prozrachnom gazovom kol'ce, vrashayushemsya vokrug zvezdy. Odnako dlya ob'yasneniya vseh osobennostei takih spektrov gipoteza Struve nedostatochna. Neobhodimo takzhe dopustit' nalichie processa istecheniya materii, nosyashego peremennyi harakter. S drugoi storony, po mneniyu Me Laughlin [16], ukazannye vyshe izmeneniya v spektrah zvezd tipa φ Persei mozhno ob'yasnit' predpolozheniem o pul'sacii vrashayusheisya zvezdy.
Takim obrazom obolochki zvezd tipa Be uchastvuyut, po-vidimomu, v dvuh vidah dvizheniya - vrashatel'nom i radial'nom. Voznikaet poetomu zadacha o nahozhdenii konturov spektral'nyh linii, obrazovannyh takoi obolochkoi. Struve rassmotrel etu zadachu dlya prozrachnogo vrashayushegosya kol'ca. Odnako predstavlyaet interes reshenie toi zhe zadachi dlya bolee obshego sluchaya (vrashenie plyus radial'noe dvizhenie) pri neprozrachnosti obolochki dlya izlucheniya v liniyah.
My vychislim seichas kontury linii, obrazovannyh vrashayusheisya i rasshiryayusheisya obolochkoi, dlya predel'nogo sluchaya, ukazannogo vyshe (v >> u). Pri etom my snova budem schitat', chto skorost' rasshireniya odinakova dlya vseh sloev. Chto zhe kasaetsya skorosti vrasheniya, to my primem, chto eta skorost' ubyvaet obratno proporcional'no rasstoyaniyu ot centra zvezdy, t. e. imeet mesto sohranenie uglovogo momenta.
Rassmotrim dlya prostoty ekvatorial'nuyu ploskost' zvezdy. Pust' $v'(r) = v'(r_0)\, \frac{r_0}{r}$ ust' skorost' vrasheniya i $v^{\prime\prime}$ - skorost' rasshireniya atmosfery. Togda luchevaya skorost' budet ravna

$v = v'(r_0)\left(\frac{r_0}{r} \sin\theta + k\cos\theta \right),$ (36)

gde $k = \frac{v^{\prime\prime}}{v'(r_0)}$ .
Kontury linii poglosheniya, vychislennye nami dlya dvuh sluchaev: k = 0 ("chistoe" vrashenie) i k = 1/3 dlya dvuh zakonov potemneniya (34), dany na chert. 4 [pri etom velichina y snova opredelyaetsya sootnosheniem (33), v kotorom pod v teper' ponimaetsya skorost' v'(r₀)].

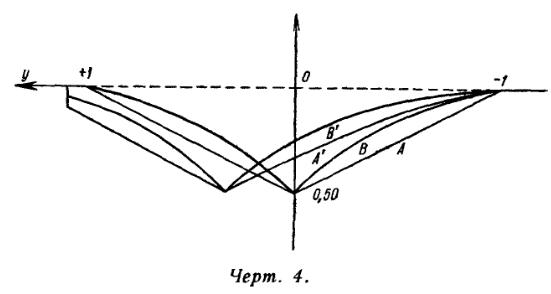
Naidem teper' kontury linii izlucheniya. Pust' E_ν est' kolichestvo energii chastoty ν, izluchaemoi ekvatorial'nym sloem v edinichnom telesnom ugle. Dlya etoi velichiny my nahodim

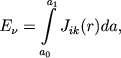
$E_{\nu} = \int\limits_{a_0}^{a_1} J_{ik}(r)da ,$ (37)

gde $a=r\sin\theta$ , a predely integrirovaniya opredelyayutsya iz sootnoshenii:

$a_0 = r_0 \sin\theta_0, \quad \sin\theta_0 + k\cos\theta_0 = y,$ (38)

$a_1 = r_1 \sin\theta_1, \quad \frac{r_0}{r_1} \sin\theta_1 + k\cos\theta_1 = y,$ (39)

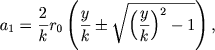
$a_1 = \frac{2}{k} r_0 \left(\frac{y}{k} \pm\sqrt{\left(\frac{y}{k}\right)^2 - 1}\right) ,$ (40)

prichem beretsya odno iz sootnoshenii (39) ili (40), v zavisimosti ot togo, peresekayutsya krivye ravnyh luchevyh skorostei s okruzhnost'yu radiusa r₁ ili net Velichina zhe J_ik(r) kak i ran'she, opredelyaetsya formuloi (27).
Dlya vychisleniya integrala (37) nado znat' zavisimost' velichin $\frac{n_i}{n_k}$ ot radiusa, dlya chego dlya dannogo sluchaya neobhodimo vyrazit' parametr x, ot kotorogo otnoshenie $\frac{n_i}{n_k}$ zavisit, v vide funkcii ot r (sm. predydushii paragraf). Dlya prostoty my polozhim J_ik = const. Togda vmesto (37) poluchaem

$E_\nu = J_{ik}(a_1 - a_0).$ (41)

Dlya sluchaya chistogo vrasheniya eta formula privoditsya k vidu:

$\left. \begin{array}{lr} E_\nu = J_{ik} r_0 y\left[\left(\frac{r_1}{r_0}\right)^2 - 1\right],& \qquad \mbox{esli} |y| < \frac{r_0}{r_1} \\ E_\nu = J_{ik} r_0 y\left[\frac{1}{y^2} - 1 \right],& \qquad \mbox{esli} |y| > \frac{r_0}{r_1} \end{array} \right\}$ (42)

Kontury linii izlucheniya, vychislennye po formulam (41) i (42) dlya sluchaev: $k=0\left(\frac{r_1}{r_0}=2,\frac{r_1}{r_0}=4\right) \mbox{i} \, k=\frac{1}{3}\left(\frac{r_1}{r_0}=2\right)$ , privedeny na chert. 5. Eti linii dolzhny byt' nalozheny na linii poglosheniya, primery kotoryh dany na chert. 4.

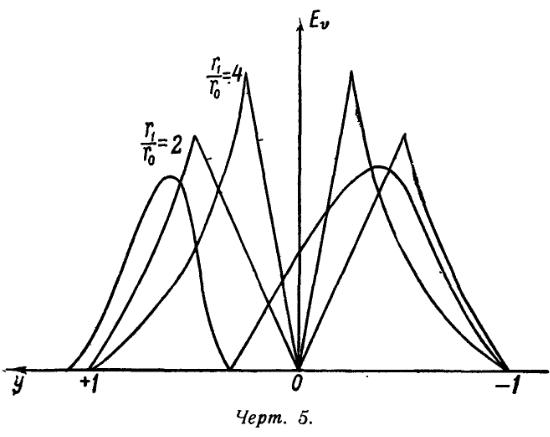
Iz rassmotreniya privedennyh formul i chertezhei mozhno sdelat' sleduyushie vyvody:

Voobshe govorya, vychislennye kontury ves'ma pohozhi na kontury linii v spektrah zvezd tipa Be. V sluchae chistogo vrasheniya oba komponenta yarkih linii okazyvayutsya odinakovymi, v sluchae vrasheniya i rasshireniya - yarkie linii smesheny v fioletovuyu storonu spektra, i fioletovyi komponent slabee krasnogo. Imenno poslednego roda linii chashe vstrechayutsya v spektrah zvezd tipa Be. Ukazannyi fakt svidetel'stvuet ob istechenii materii iz etih zvezd.

Esli by my rassmotreli vrashayushuyusya i szhimayushuyusya atmosferu, to poluchili by yarkie linii, smeshennye v krasnuyu storonu spektra, i krasnyi komponent okazalsya by slabee fioletovogo. Takie kontury, vmeste s poluchennymi vyshe dlya vrashayusheisya i rasshiryayusheisya atmosfery, podtverzhdayut gipotezu Mc Laughlin o pul'sacii vrashayushihsya atmosfer v sluchae zvezd tipa φ Persei.

Vychislennye yarkie linii okazyvayutsya, voobshe govorya, dvoinymi. Odnako rasstoyanie mezhdu komponentami tem men'she, chem men'she skorost' vrasheniya zvezdy i chem bol'she velichina r₁/r₀. Poetomu v spektrah nekotoryh zvezd komponenty dolzhny slivat'sya, i my uvidim odinochnye linii. V spektrah zhe drugih zvezd mogut nablyudat'sya kak odinochnye, tak i razdvoennye linii (ibo dlya raznyh linii velichiny - razlichny). Etim, po-vidimomu, ob'yasnyayutsya razlichiya v forme yarkih linii v spektrah zvezd tipa Be.

V sluchae protyazhennogo obrashayushego sloya polnaya intensivnost' linii poglosheniya vozrastaet s uvelicheniem skorosti vrasheniya zvezdy. Etot fakt dolzhen byt' otmechen potomu, chto v obychnom sluchae polnaya intensivnost' absorbcionnoi linii ne menyaetsya pri rasshirenii linii, vsledstvie vrasheniya zvezdy.

My vidim, chto predlozhennaya teoriya konturov spektral'nyh linii v spektrah zvezd tipov WR, P Cygni i Be, nesmotrya na ee elementarnyi harakter, nahoditsya v horoshem soglasii s nablyudeniyami. Eto govorit kak v pol'zu prinyatyh predstavlenii o dvizhenii v zvezdnyh atmosferah, tak i v pol'zu nashei tochki zreniya o vozniknovenii kak yarkih, tak i temnyh linii v odnoi i toi zhe protyazhennoi obolochke. Nam kazhetsya, chto v dal'neishem predstavit interes primenenie rezul'tatov, poluchennyh v etoi glave, k izucheniyu atmosfer konkretnyh zvezd (naprimer P Cygni, γ Cassiopeiae i dr.). Blagodarya prostote poluchennyh rezul'tatov pri etom ne vstretitsya osobyh trudnostei.

<< 2.2 Izmenenie vozbuzhdeniya vdol' radiusa | Oglavlenie | Glava III. Gazovye tumannosti >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce