Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << Glava III. Gazovye tumannosti | Oglavlenie | 3.2 Pole L_α-izlucheniya >>

3.1 Pole L_c-izlucheniya

Posle raboty Milne [6] obsheprinyatoi yavlyaetsya sleduyushaya model' planetarnoi tumannosti (i lyuboi drugoi nebulyarnoi obolochki, okruzhayushei zvezdu). Planetarnaya tumannost' predstavlyaet soboi sfericheskuyu obolochku, tolshina kotoroi mala po sravneniyu s ee rasstoyaniem ot centra zvezdy. Vsledstvie etogo obolochka mozhet schitat'sya sostoyashei iz plosko-parallel'nyh sloev, a koefficient dilyucii v obolochke - postoyannym.

Pust' χ_1c srednii atomnyi koefficient poglosheniya za granicei serii Laimana i τ - sootvetstvuyushaya opticheskaya glubina, otschitannaya ot vnutrennei granicy obolochki. Pust' dalee πS_1c - polnoe kolichestvo L_c-kvantov, padayushih ot zvezdy na 1 sm² vnutrennei granicy obolochki i K_1c(τ₁θ) - chislo kvantov diffuznogo L_c-izlucheniya, prohodyashih na glubine τ pod uglom θ k vneshnei normali v edinichnom telesnom ugle cherez edinichnuyu ploshadku, perpendikulyarnuyu k lucham.

Tak kak chislo ionizacii, proishodyashih iz osnovnogo sostoyaniya, dolzhno ravnyat'sya chislu zahvatov na vse urovni, to my poluchaem

$n_1 \chi_{1c}\int K_{1c}d\omega + n_1 \chi_{1c}\pi S_{1c} e^{-\tau} = n_e n^+ \sum\limits_1^\infty C_i .$ (1)

Oboznachaya cherez p dolyu zahvatov na pervyi uroven' i vvodya velichinu C_1c, opredelennuyu sootnosheniem

$n_e n^+ C_1 = 4 \pi n \chi_{1c} C_{1c} ,$ (2)

Vmesto (1) nahodim

$C_{1c} = p\int K_{1c} \frac{d\omega}{4\pi} + p \frac{S_{1c}}{4} e^{-\tau} .$ (3)

S drugoi storony, velichiny C_1c i K_1c svyazany drug s drugom obychnym uravneniem perenosa izlucheniya

$\cos\theta\frac{dK_{1c}}{d\tau} = C_{1c}-K_{1c}.$ (4)

Krome togo, imeyut mesto sleduyushie granichnye usloviya:

$\left. \begin{array}{l} K_{1c}(0,\theta) = K_{1c}(0,\pi - \theta) \\ K_{1c}(\tau_1,\theta) = 0 \; (\mbox{pri} \; \theta>\frac{\pi}{2}) \end{array} \right\}$ (5)

(uslovie na vnutrennei granice uchityvaet diffuznoe izluchenie, idushee s protivopolozhnoi storony tumannosti).

Takim obrazom zadacha ob opredelenii stepeni ionizacii v tumannosti svoditsya k resheniyu uravnenii (3) i (4) pri granichnyh usloviyah (5).

Iz etih uravnenii poluchaetsya sleduyushee integral'noe uravnenie dlya opredeleniya velichiny C_1c(τ):

$C_{1c}(\tau) = \frac{p}{2}\int\limits_0^{\tau_1} [Ei|\tau-\tau'| + Ei(\tau+\tau')]C_{1c}(\tau') d\tau' + p\frac{S_{1c}}{4}e^{-\tau} .$ (6)

Pri τ = ∞ i na bol'shih opticheskih glubinah vmesto uravneniya (6) poluchaem

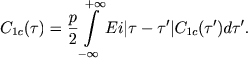
$C_{1c}(\tau) = \frac{p}{2}\int\limits_{-\infty}^{+\infty} Ei|\tau-\tau'|C_{1c}(\tau') d\tau' .$ (7)

Eto uravnenie imeet tochnoe reshenie

$C_{1c}(\tau)=Ae^{-k\tau} ,$ (8)

gde k - koren' uravneniya

$\frac{p}{2k} \ln\frac{1+k}{1-k} = 1 ,$ (9)

a A - proizvol'naya postoyannaya. My budem rassmatrivat' funkciyu (8) kak priblizhennoe reshenie uravneniya (6) i naidem postoyannuyu A iz togo usloviya, chtoby uravnenie (6) udovletvoryalos' tochno v srednem. Togda dlya A poluchaem

$A=\frac{kpS_{1c}}{4(1-p)} .$ (10)

Velichina r yavlyaetsya funkciei ot elektronnoi temperatury. Dlya planetarnyh tumannostei mozhno, prinyat' r = 1/2. Togda iz uravneniya (9) nahodim k = 0,96. My vidim, chto naidennoe nami vyrazhenie dlya funkcii C_1c(τ) sravnitel'no malo otlichaetsya ot vyrazheniya, poluchayushegosya pri uchete tol'ko pryamogo izlucheniya, idushego ot zvezdy. Vsledstvie etogo my mozhem schitat', chto stepen' ionizacii v tumannosti menyaetsya po zakonu

$n_e\frac{n^+}{n_1} = W\sqrt{\frac{T_e}{T_*}}\frac{(2\pi mkT_*)^{\frac{3}{2}}}{h^3} e^{-\frac{h\nu_{1c}}{kT_*}} \cdot 2e^{-\tau} .$ (11)

Sleduet otmetit' dva obstoyatel'sva:

Pri reshenii uravnenii (3) i (4) priblizhennymi metodami dlya k poluchaem: k = 2(1-p)^½ (metodam Shvarcshil'da-Shustera) i k = (3(1-p))^½ (metodom Eddingtona). Razlichie mezhdu etimi znacheniyami k i tem znacheniem, kotoroe poluchaetsya iz uravneniya (9), dlya mnogih voprosov, nesomnenno, sushestvenno. Odnako dlya planetarnyh tumannostei, iz-za bol'shoi roli pryamogo izlucheniya, priblizhennye metody ne privodyat k ser'eznym oshibkam.
Vyshe ves' laimanovskii kontinuum my zamenili odnim urovnem, prinyav nekotoryi srednii koefficient poglosheniya. Bolee tochnaya traktovka voprosa byla dana Menzel s sotrudnikami [4], sostavivshimi uravnenie luchevogo ravnovesiya dlya kazhdogo intervala chastot (pri etom byli uchteny ne tol'ko fotoionizacii i zahvaty, no i stolknoveniya: elektronov drug s drugom i free-free transitions). Legko videt', odnako, chto v etom net neobhodimosti, tak kak energiya, izluchaemaya elementarnym ob'emom tumannosti za granicei serii Laimana, yavlyaetsya izvestnoi funkciei ot chastoty 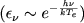$(\epsilon_{\nu} \sim e^{-\frac{h\nu}{kT_e}})$ . Poetomu i pri bolee tochnom rassmotrenii voprosa my snova prihodim k integral'nomu uravneniyu tipa (6) (s neskol'ko bolee slozhnym yadrom) dlya odnoi neizvectnoi funkcii, zavisyashei tol'ko ot τ .

<< Glava III. Gazovye tumannosti | Oglavlenie | 3.2 Pole L_α-izlucheniya >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

3.1 Pole Lc-izlucheniya

3.1 Pole L_c-izlucheniya