Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << 3.1 Pole L_c-izlucheniya | Oglavlenie | 3.3 Temperatury tumannostei i temperatury yader >>

3.2 Pole L_α-izlucheniya

Pri rassmotrenii polya L_c-izlucheniya dlya nas ne imelo znacheniya, dvizhetsya obolochka ili net (poskol'ku skorosti dvizheniya obolochki mala po sravneniyu so skorost'yu sveta). Teper' zhe my dopustim, chto obolochka dvizhetsya (skazhem, rasshiryaetsya) i pritom s gradientom skorosti. Dlya prostoty predpolozhim, chto $\frac{dv}{d\tau}=const \; \mbox{i} \; \frac{dv}{d\tau}>0$ .

Tak zhe kak i ran'she, my budem schitat', chto koefficient poglosheniya v linii yavlyaetsya postoyannym v intervale Δν₁₂ i raven nulyu vne etogo intervala. Pri nalichii gradienta skorosti nekotoraya chast' L_α-kvantov, prihodyashih v dannoe mesto obolochki (chastoty kotoryh ne popadayut v ukazannyi interval), ne budut pogloshat'sya v etom meste. Vsledstvie etogo integral'noe uravnenie, opredelyayushee plotnost' L_α-izlucheniya, budet imet' sovsem drugoi vid, chem pri otsutstvii gradienta skorosti.

Perehodya k sostavleniyu etogo uravneniya, uslovimsya v tom, chto, govorya o plotnosti L_α-izlucheniya, my budem imet' v vidu tol'ko te L_α-kvanty iz nahodyashihsya v dannom ob'eme, kotorye mogut byt' poglosheny v etom ob'eme.

Budem ishodit' iz usloviya stacionarnosti dlya vtorogo urovnya vodorodnogo atoma:

$n_2 A_{21} = n_1 B_{12} \rho_{12} + \sum\limits_3^\infty n_k A_{k2} + n_e n^+ C_2 .$ (12)

Tak kak obolochka predpolagaetsya prozrachnoi dlya izlucheniya v liniyah subordinatnyh serii, to my imeem

$\sum\limits_3^\infty n_k A_{k2} = n_e n^+ \sum\limits_3^\infty C_k .$ (13)

Podstavlyaya (13) v (12) i uchityvaya rezul'taty predydushego paragrafa, poluchaem

$n_2 A_{21} = n_1 B_{12} \rho_{12} + n_1 \chi_{1c} k\pi S_{1c} e^{-k\tau} .$ (14)

Polozhim

$\frac{k}{4} S_{1c} e^{-k\tau} = \psi(\tau)$ (15)

i

$n_2 A_{21} = 4\pi n_1 \chi_{12} C_{12}, \quad n_1 B_{12} \rho_{12} = n_1 \chi_{12}\int K_{12} d\omega ,$ (16)

gde χ₁₂ - srednii atomnyi koefficient poglosheniya v linii L_α. Togda vmesto (13) nahodim

$C_{12} = \int K_{12}\frac{d\omega}{4\pi} + q\psi(\tau) .$ (17)

gde oboznacheno $q=\frac{\chi_{1c}}{\chi_{12}}$ .

V rassmatrivaemom sluchae, t.e. pri nalichii gradienta skorosti v obolochke, vtorym uravneniem, svyazyvayushim velichiny S₁₂ i K₁₂, uzhe ne mozhet sluzhit' obychnoe uravnenie perenosa izlucheniya. Vmesto etogo uravneniya, s pomosh'yu teh zhe soobrazhenii, kotorye byli izlozheny v glave I, my poluchaem sleduyushee bolee slozhnoe integral'noe sootnoshenie:

$K_{12}(t,\theta) = \int\limits_0^t C_{12}(t')e^{-(t-t')\sec\theta} [1-\beta(t-t')\cos\theta]\sec\theta dt' \qquad (\theta<\frac{\pi}{2}) ,$ (18)

gde cherez t oboznachena opticheskaya glubina v linii L_α, a velichina β imeet prezhnee znachenie, t.e.

$\beta=\frac{q}{2u}\frac{dv}{d\tau} .$ (19)

My prenebregli zdes' izlucheniem v linii L_α, padayushim na vnutrennyuyu granicu obolochki, kak ot zvezdy, tak i ot protivopolozhnyh chastei obolochki (poslednee oznachaet, chto skorost' rasshireniya vnutrennei granicy my schitaem dostatochno bol'shoi po sravneniyu so srednei termicheskoi skorost'yu atomov).

Podstavlyaya sootnoshenie (18) (i analogichnoe sootnoshenie dlya uglov θ, bol'shih π/2 v uravnenie (17), my poluchaem sleduyushee integral'noe uravnenie, opredelyayushee velichinu S₁₂:

$C_{12}(t) = \frac{1}{2}\int\limits_0^{t_1} C_{12}(t')[Ei|t-t'|-\beta Ei_2|t'-t|\cdot|t'-t|]dt'+q\psi(\tau) ,$ (20)

gde

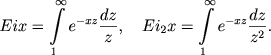
$Eix = \int\limits_1^{\infty} e^{-xz} \frac{dz}{z}, \quad Ei_2 x = \int\limits_1^{\infty} e^{-xz} \frac{dz}{z^2} .$ (21)

Tak kak my schitaem, chto opticheskaya tolshina τ tumannosti za granicei serii Laimana bol'she edinicy, to opticheskaya tolshina t₁ v linii L_α dolzhna byt' bol'she 10⁴. Poetomu dlya srednih chastei tumannosti predely integrirovaniya v (20) mozhno zamenit' na beskonechnye. Legko ubedit'sya, chto reshenie poluchennogo takim obrazom uravneniya imeet vid

$C_{12}(t)=Ae^{-kt} + Be^{kt} + 3\frac{q}{\beta}\psi(\tau),$ (22)

gde k - koren' uravneniya

$\frac{1}{2k}\ln\frac{1+k}{1-k} - \frac{\beta}{k^2}\left[1+\frac{1}{1-k^2} - \frac{1}{k}\ln\frac{1+k}{1-k}\right]=1 ,$ (23)

a A i B - proizvol'nye postoyannye.

V forme (22) my budem iskat' reshenie uravneniya (20), opredelyaya postoyannye A i V iz uslovii vblizi granic. Podstavlyaya (22) v (20) i schitaya, chto t malo, poluchaem

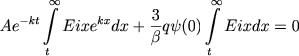
$Ae^{-kt}\int\limits_t^\infty Eixe^{kx}dx + \frac{3}{\beta} q\psi(0)\int\limits_t^\infty Eixdx = 0$ (24)

Zastavlyaya eto uravnenie vypolnyat'sya tochno v srednem, nahodim

$A=\frac{3}{2}\frac{q}{\beta}\frac{k^2}{\ln(1-k)+k}\psi(0) .$ (25)

Sovershenno analogichno poluchaem vyrazheniya dlya B

$B=\frac{3}{2}\frac{q}{\beta}\frac{k^2}{\ln(1-k)+k}\psi(\tau_1)e^{-kt_1} .$ (26)

Tak kak velichina β mala, to iz (23) priblizhenno sleduet

$k=\sqrt{\beta} .$ (27)

Poetomu okonchatel'no reshenie uravneiya (20) mozhno zapisat' v vide

$C_{12}(t)=3\frac{q}{\beta} \left\{ \psi(\tau) - \left(1-\frac{2}{3} \sqrt{\beta}\right) \left[\psi(0)e^{-t\sqrt{\beta}}+\psi(\tau_1)e^{-(t_1 - t)\sqrt{\beta}}\right]\right\} .$ (28)

Krome velichiny C₁₂(t), nas interesuet takzhe potok L_α-kvantov, opredelyayushii svetovoe davlenie v tumannosti. Prenebregaya chlenom s mnozhitelem β, dlya etogo potoka imeem

$F(t) = 2\pi\left[\int\limits_0^t E_{i_2} (t-t')C_{12}(t')dt' - \int\limits_t^{t'} E_{i_2} (t'-t)C_{12}(t')dt'\right].$ (29)

Dlya srednih chastei tumannosti eta formula daet

$F(t) = -4\pi\frac{q^2}{\beta}\frac{d\psi}{d\tau}.$ (30)

Na granicah zhe potok raven

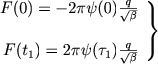
$\left. \begin{array}{r} F(0)=-2\pi\psi(0)\frac{q}{\sqrt{\beta}} \\ \\ F(t_1)=2\pi\psi(\tau_1)\frac{q}{\sqrt{\beta}} \end{array} \right\}$ (31)

Rassmotrim teper' dlya sravneniya tumannost', rasshiryayushuyusya bez gradienta skorosti. V etom sluchae v uravnenii (20) nado polozhit' β=0. Togda dlya srednih chastei tumannosti reshenie uravneniya (20) budet imet' vid

$C_{12}(t)=3\psi(0)\frac{t_1-t}{qt_1}.$ (32)

Dlya potoka L_α-izlucheniya na vnutrennei granice tumannosti bez vsyakih vychislenii poluchaem

$F(0)=-4\pi\psi(0)$ (33)

(tak kak pri otsutstvii gradienta skorosti potok L_α-kvantov na vnutrennei granice dolzhen byt' raven potoku L_c-kvantov, idushih ot central'noi zvezdy).

Sravnivaya formuly (32) i (33) sootvetstvenno s formulami (28) i (31), my vidim, chto poyavlenie gradienta skorosti v tumannosti chrezvychaino rezko ponizhaet plotnost' i potok L_α-izlucheniya. Dopustim, naprimer, chto skorosti $\frac{dv}{d\tau} \; \mbox{i} \; u$ odnogo poryadka. Togda pervaya iz formul (31) daet dlya potoka L_α-izlucheniya na vnutrennei granice tumannosti znachenie v neskol'ko sot raz men'shee, chem formula (33). A dlya plotnosti L_α-izlucheniya v srednih chastyah tumannosti po formule (28) poluchaetsya znachenie v neskol'ko desyatkov tysyach raz men'she, chem po formule (32).

Kak uzhe ukazyvalos', pole L_α-izlucheniya v tumannosti, dvizhusheisya bez gradienta skorosti, vpervye bylo rassmotreno V. A. Ambarcumyanom. Pri etom byla vyyasnena bol'shaya rol' svetovogo davleniya, vyzvannogo L_α-izlucheniem. Podschety pokazali, chto na vnutrennei granice tumannosti svetovoe davlenie primerno v 1000 raz prevoshodit silu lrityazheniya central'noi zvezdy. Etot vyvod yavlyalsya vazhnym po dvum prichinam: vo-pervyh, potomu, chto on otkryval perspektivy postroeniya dinamiki tumannosti pri uchete tol'ko odnoi sily - svetovogo davleniya, obuslovlennogo L_α-izlucheniem; i, vo-vtoryh, potomu, chto on ukazyval na sil'noe tormozhenie vnutrennih chastei tumannosti i tem samym podkreplyal gipotezu o proishozhdenii planetarnyh tumannostei iz obolochek sverhnovyh zvezd. (Kak izvestno, obolochki sverhnovyh zvezd vybrasyvayutsya s ogromnymi skorostyami poryadka neskol'kih tysyach kilometrov v sekundu, a planetarnye tumannosti rasshiryayutsya so skorostyami poryadka neskol'kih desyatkov kilometrov v sekundu; ob'yasnenie etogo razlichiya odnim tol'ko gravitacionnym tormozheniem yavlyaetsya nepravdopodobnym).

Odnako v deistvitel'nosti neobhodimo schitat', chto tumannost' dvizhetsya s gradientom skorosti (ibo esli by v nekotoryi moment vremeni tumannost' i dvigalas' s postoyannoi dlya vseh sloev skorost'yu, to postepenno, blagodarya svetovomu davleniyu, vse ravno sozdalas' by raznost' skorostei rasshireniya). No poyavlenie gradienta skorosti, kak pokazano vyshe, rezko umen'shaet potok L_α-izlucheniya. Poetomu my prihodim k vyvodu, chto svetovoe davlenie, vyzvannoe L_α-izlucheniem, ne igraet v tumannosti toi bol'shoi roli, kotoraya emu ran'she pripisyvalas'.

Sleduet otmetit', chto zadacha, reshennaya nami v etom paragrafe, byla ran'she rassmotrena Zanstra [5], Odnako metod, prinyatyi Zanstra, otlichaetsya ot nashego. Zanstra, rassmatrivaya tumannost', ogranichennuyu parallel'nymi ploskostyami, uchityval tol'ko tu sostavlyayushuyu skorosti atoma, kotoraya perpendikulyarna k etim granicam. Priblizhenno on schital, chto esli eta sostavlyayushaya odinakova dlya atomov, to oni mogut pogloshat' izluchenie drug ot druga; esli razlichny, to ne mogut.

Yasno, chto pri takom predpolozhenii bystro letyashie atomy okazyvayutsya sposobnymi pogloshat' (a znachit i izluchat') lish' ochen' nebol'shoe kolichestvo energii, tak kak oni lishayutsya vozmozhnosti pogloshat' izluchenie, idushee s bokov. Poetomu kontur linii izlucheniya, obrazovannoi elementarnym ob'emom, poluchaetsya ne pryamougol'nyi, a parabolicheskii. Eta raznica okazyvaetsya ochen' sushestvennoi, tak kak vo vtorom sluchae dolya nepogloshaemoi energii budet znachitel'no men'she, chem v pervom. Vsledstvie etogo plotnost' i potok L_α-izlucheniya, poluchennye metodom Zanstra, dolzhny rezko otlichat'sya ot nashih.

Tak eto i est' na samom dele. Vzyav zanstrovskoe znachenie potoka L_α-izlucheniya iz knigi V. A. Ambarcumyana [7]

$F(t)=-\frac{\pi}{3}\left(\frac{q}{\beta}\right)^2\frac{d\psi}{d\tau}$ (34)

i sravniv ego s nashim znacheniem [sm. formulu (30)], my vidim, chto raznica mezhdu resheniyami ogromna. Esli, naprimer, prinyat', chto skorosti $\frac{dv}{d\tau} \; \mbox{i} \; u$ odnogo poryadka, to poluchaetsya, chto zanstrovskii potok, budet primerno v 10000 raz bol'she, chem nash. Poetomu nado priznat', chto reshenie Zanstra yavlyaetsya prosto nevernym.*

Sushnost' oshibki Zanstra sostoit v tom, chto on ne uchityvaet izmeneniya chastoty svetovyh kvantov, proishodyashego pri elementarnom akte rasseyaniya, vsledstvie molekulyarnogo effekta Dopplera, t. e. schitaet, chto rasseyanie sveta yavlyaetsya kogerentnym. Dlya dvizhusheisya sredy, dlya kotoroi effekt Doplera voobshe igraet ogromnuyu rol', eta oshibka brosaetsya v glaza. Odnako nekogerentnost' rasseyaniya sveta imeet bol'shoe znachenie i dlya nepodvizhnyh atmosfer. Vvidu vazhnosti etogo voprosa my v dal'neishem posvyatim emu otdel'noe issledovanie.

* To zhe samoe nado skazat' i o drugoi rabote Zanstra [8], v kotoroi dano primenenie rezul'tatov ego pervoi raboty k dinamike gazovyh tumannostei.

<< 3.1 Pole L_c-izlucheniya | Oglavlenie | 3.3 Temperatury tumannostei i temperatury yader >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

3.2 Pole Lα-izlucheniya

3.2 Pole L_α-izlucheniya