3.3 Temperatury tumannostei i temperatury yader
V predydushih paragrafah my rassmotreli usloviya stacionarnosti dlya pervogo i vtorogo urovnei vodorodnogo atoma. Teper' my rassmotrim eshe odno uslovie stacionarnosti - zakon sohraneniya energii dlya svobodnyh elektronov tumannosti.
My budem predpolagat', chto svobodnye elektrony poluchayut energiyu pri fotoionizacii vodorodnyh atomov, a teryayut ee tremya putyami:
- pri zahvatah protonami i pri free-free transitions;
- pri stolknoveniyah, vozbuzhdayushih linii N i N "nebuliya", i
- pri neuprugih stolknoveniyah s atomami vodoroda.
Ochevidno, chto esli pri matematicheskom predstavlenii etogo zakona nam udastsya ogranichit'sya lish' izvestnymi iz nablyudenii velichinami, to my poluchim vazhnoe sootnoshenie, svyazyvayushee temperaturu central'noi zvezdy i elektronnuyu temperaturu tumannosti.
Pust' ε - srednyaya energiya, poluchaemaya elektronom pri fotoionizacii. Tak kak chislo ionizacii dolzhno ravnyat'sya chislu rekombinacii, to kolichestvo energii, poluchaemoe elektronami v 1 sm3 za 1 sek., budet ravno ![]() . Chast' etoi energii, teryaemoi pri rekombinaciyah i free-free transitions, my oboznachim cherez
. Chast' etoi energii, teryaemoi pri rekombinaciyah i free-free transitions, my oboznachim cherez ![]() , druguyu chast', perehodyashuyu v izluchenie linii "nebuliya" cherez E i, nakonec, tret'yu chast', rashoduemuyu pri stolknoveniyah s vodorodnymi atomami, cherez
, druguyu chast', perehodyashuyu v izluchenie linii "nebuliya" cherez E i, nakonec, tret'yu chast', rashoduemuyu pri stolknoveniyah s vodorodnymi atomami, cherez ![]() .
.
Zakon sohraneniya energii daet
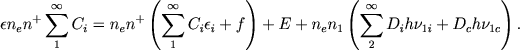
|
(35) |
Zdes' nam neizvestna velichina E, ibo my ne znaem ni effektivnyh sechenii dlya stolknovenii elektronov s atomami OIII, ni koncentracii etih atomov. No etu velichinu mozhno naiti inache, esli schitat' izvestnym otnoshenie intensivnostei linii N2/Hβ.
Uchityvaya, chto N1/N2=3, my imeem
|
|
(36) |
gde integrirovanie rasprostranyaetsya po vsemu ob'emu tumannosti, a ![]() - velichina, opredelyaemaya iz uravnenii Cillie(I, 12).
- velichina, opredelyaemaya iz uravnenii Cillie(I, 12).
Integriruya (35) po ob'emu tumannosti i prinimaya vo vnimanie (36), poluchaem
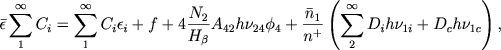
|
(37) |
|
|
(38) |
|
|
(39) |
Velichina ![]() est' energiya, poluchaemaya elektronom pri fotoionizacii, srednyaya dlya vsei tumannosti. Voobshe govorya, ona zavisit ot temperatury central'noi zvezdy i ot opticheskoi tolshiny tumannosti za granicei serii Laimana. My rassmotrim dva krainih sluchaya: 1) tumannost' pogloshaet nebol'shuyu chast' izlucheniya zvezdy (τ1 << 1) i 2) tumannost' pogloshaet vsyu energiyu zvezdy za granicei serii Laimana (τ1 >> 1).
V pervom sluchae mozhno schitat', chto e opredelyaetsya lish' ioniziruyushim izlucheniem, idushim neposredstvenno ot zvezdy. Poetomu, polagaya
est' energiya, poluchaemaya elektronom pri fotoionizacii, srednyaya dlya vsei tumannosti. Voobshe govorya, ona zavisit ot temperatury central'noi zvezdy i ot opticheskoi tolshiny tumannosti za granicei serii Laimana. My rassmotrim dva krainih sluchaya: 1) tumannost' pogloshaet nebol'shuyu chast' izlucheniya zvezdy (τ1 << 1) i 2) tumannost' pogloshaet vsyu energiyu zvezdy za granicei serii Laimana (τ1 >> 1).
V pervom sluchae mozhno schitat', chto e opredelyaetsya lish' ioniziruyushim izlucheniem, idushim neposredstvenno ot zvezdy. Poetomu, polagaya
|
|
(40) |
gde k - postoyannaya Bol'cmana, my dlya velichiny A poluchaem
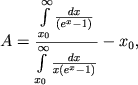
|
(41) |
Vo vtorom sluchae fotoionizaciya proishodit kak blagodarya izlucheniyu, idushemu ot zvezdy, tak i blagodarya diffuznomu izlucheniyu samoi tumannosti. Pri bol'shih τ1 mozhno, odnako, schitat', chto vse kvanty, ispuskaemye pri zahvatah elektronov na pervyi uroven', pogloshayutsya v samoi tumannosti, t. e. chto chislo ionizacii, proishodyashih pod vliyaniem diffuznogo izlucheniya, ravno ![]() , a energiya, kotoruyu elektrony poluchayut pri etom, ravna
, a energiya, kotoruyu elektrony poluchayut pri etom, ravna ![]() . Poetomu i v dannom sluchae diffuznogo izlucheniya tumannosti mozhno ne uchityvat'. Nado tol'ko Ci i Cisi summirovat', ne ot 1, a ot 2. Dlya A my teper' nahodim
. Poetomu i v dannom sluchae diffuznogo izlucheniya tumannosti mozhno ne uchityvat'. Nado tol'ko Ci i Cisi summirovat', ne ot 1, a ot 2. Dlya A my teper' nahodim
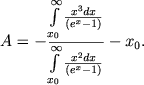
|
(42) |
Znacheniya velichiny A, vychislennye po formulam (41) i (42), privedeny v tabl. XI.
Tablica XI
| T∗/1000 | I | II | ||
| A | AT∗/1000 | A | AT∗/1000 | |
| 20 | 0,90 | 18 | 1,24 | 25 |
| 40 | 0,83 | 33 | 1,46 | 58 |
| 60 | 0,77 | 46 | 1,63 | 98 |
| 80 | 0,71 | 57 | 1,76 | 141 |
V dopolnenie k ravenstvu (6) polozhim:
|
|
(43) |
|
|
(44) |
|
|
(45) |
Togda vmesto (37) poluchaem
|
|
(46) |
Eto est' okonchatel'nyi vid sootnosheniya, svyazyvayushego temperaturu yadra s elektronnoi temperaturoi tumannosti. Chtoby primenit' eto sootnoshenie k konkretnym tumannostyam, nado eshe vychislit' koefficienty V, S i D, a takzhe dat' formuly dlya nahozhdeniya srednei stepeni ionizacii v tumannosti.
Dlya vychisleniya koefficientov V, S i D my imeem sleduyushie formuly. Soglasno Cillie (sm. stat'yu, citirovannuyu v glave I), energiya, izluchaemaya 1 sm3 za 1 sek. pri free-free transitions, ravna
|
|
(47) |
a energiya, izluchaemaya pri zahvate na i-i uroven', ravna
|
|
(48) |
Pri nashih oboznacheniyah pervoe iz etih vyrazhenii est' nen+ƒ , a vtoroe - nen+Ci(εi+hνic).
Soglastno Shotaro Mlyamoto [9], dlya velichiny Di imeem
|
|
(49) |
gde ![]() - srednee effektivnoe sechenie dlya vozbuzhdeniya i-go sostoyaniya ot normal'nogo. Mozhno prinyat', chto znacheniya
- srednee effektivnoe sechenie dlya vozbuzhdeniya i-go sostoyaniya ot normal'nogo. Mozhno prinyat', chto znacheniya ![]() dayutsya tablicei:
dayutsya tablicei:
| i | 2 | 3 | 4 | 5 |
| 1,0 | 0,2 | 0,1 | 0,06 |
esli vyrazhat' ![]() v edinicah a02π = 0,88 ⋅ 10-16 sm2. Velichina Dc opredelyaetsya formuloi, analogichnoi (49), prichem v etom sluchae
v edinicah a02π = 0,88 ⋅ 10-16 sm2. Velichina Dc opredelyaetsya formuloi, analogichnoi (49), prichem v etom sluchae ![]() = 0,2 i vmesto hν1c stoit energiya ionizacii hν1i.
= 0,2 i vmesto hν1c stoit energiya ionizacii hν1i.
Znacheniya koefficientov V, S i D, vychislennye s pomosh'yu vysheukazannyh formul, privedeny v tabl. XII.
Tablica XII
| Te/1000 | B | BTe/1000 | C/1000 | D/1000 |
| 5 | 1,02 | 5 | 12 | 0,001 |
| 7,5 | 1,04 | 8 | 12 | 3,0 |
| 10 | 1,06 | 11 | 12 | 250 |
| 12,5 | 1,08 | 14 | 12 | 2500 |
| 15 | 1,10 | 17 | 12 | 16000 |
Iz tabl. XII, mezhdu prochim, vidno, chto koefficient D menyaetsya s elektronnoi temperaturoi ochen' bystro. Eto znachit, chto velichinu ![]() , vhodyashuyu v sootnoshenie (46), dostatochno znat' lish' priblizhenno. My mozhem ukazat', naprimer, sleduyushii sposob dlya nahozhdeniya etoi velichiny.
, vhodyashuyu v sootnoshenie (46), dostatochno znat' lish' priblizhenno. My mozhem ukazat', naprimer, sleduyushii sposob dlya nahozhdeniya etoi velichiny.
Prinimaya, chto stepen' ionizacii v tumannosti menyaetsya soglasno zakonu (11), my poluchaem
|
|
(50) |
gde ![]() est' stepen' ionizacii, opredelyaemaya obychnoi ionizacionnoi formuloi [t.e. formuloi (11) pri τ=0]. Dlya nahozhdeniya velichiny
est' stepen' ionizacii, opredelyaemaya obychnoi ionizacionnoi formuloi [t.e. formuloi (11) pri τ=0]. Dlya nahozhdeniya velichiny ![]() nado znat' koefficient delyucii i elektronnuyu plotnost' pri τ=0. Ispol'zuya horosho izvestnye formuly
nado znat' koefficient delyucii i elektronnuyu plotnost' pri τ=0. Ispol'zuya horosho izvestnye formuly
|
|
(51) |
|
|
(52) |
|
|
(53) |
gde m∗ - fotograficheskaya velichina yadra i D" - uglovoi diametr tumannosti v sekundah dugi. Drugaya interesuyushaya nac velichina - chislo svobodnyh elektronov v 1 sm3 pri τ=0 - mozhet byt' naidena iz formuly
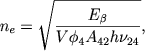
|
(54) |
gde Eβ - energiya, izluchaemaya tumannost'yu v linii Hβ. Prinimaya, chto na dolyu linii Hβ prihoditsya 1/15 chast' polnoi anergii, izluchaemoi tumannost'yu v vidimoi chasti spektra, i chto tolshina tumannosti ravna 1/10 chasti ee radiusa, vmesto (54)) poluchaem
|
|
(55) |
gde mn - vidimaya velichina tumannosti i r - rasstoyanie do tumannosti v parsekah. Takim obrazom srednyuyu stepen' ionizacii v tumannosti mozhno opredelit' iz formul (50), (11) (pri τ=0), (53) i (55).
Sootnoshenie (46) mozhet byt' ispol'zovano dlya nahozhdeniya elektronnoi temperatury tumannosti, esli temperatura yadra uzhe naidena. Kak izvestno, metody dlya opredeleniya temperatur yader vpervye byli razrabotany Zanstra [10]. Odin iz etih metodov (metod "nebuliya") osnovan na predpolozhenii, chto vsya energiya, poluchaemaya svobodnymi elektronami pri fotoionieacii, idet na vozbuzhdenie linii "nebuliya". Pri pol'zovanii etim metodom temperatura yadra opredelyaetsya iz sootnosheniya
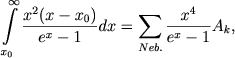
|
(56) |
v kotorom velichiny Ak (poluchennye iz nablyudenii) ravny
|
|
(57) |
gde Ek - polnaya energiya, izluchaemaya tumannost'yu v dannoi linii, a Eν∗ - energiya, izluchaemaya yadrom v edinichnom intervale chastot v tom zhe meste spektra. V deistvitel'nosti na vozbuzhdenie linii "nebuliya" rashoduetsya tol'ko dolya energii svobodnyh elektronov. Soglasno sootnosheniyu (46), eta dolya ravna ![]() . Poetomu vmesto (56) my poluchaem sleduyushee, bolee tochnoe sootnoshenie dlya opredeleniya temperatury yadra
. Poetomu vmesto (56) my poluchaem sleduyushee, bolee tochnoe sootnoshenie dlya opredeleniya temperatury yadra
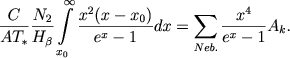
|
(58) |
Takim obrazom temperaturu tumannosti i temperaturu yadra sleduet nahodit' putem sovmestnogo resheniya uravnenii (46) i (58).
Vyvedennye uravneniya my primenili k nekotorym iz planetarnyh tumannostei. Rezul'taty vychislenii privedeny v tabl. XIII. V pervom stolbce daetsya nomer tumannosti po katalogu NGC ili JC, vo vtorom stolbce - otnoshenie
![]() , po svodke Berman [11], v tret'em - temperatura yadra, opredelennaya metodom "nebuliya", po dannym Zanstra [10], Berman [12] i Page [13], v chetvertom - ispravlennaya temperatura yadra, v pyatom - elektronnaya temperatura tumannosti,
, po svodke Berman [11], v tret'em - temperatura yadra, opredelennaya metodom "nebuliya", po dannym Zanstra [10], Berman [12] i Page [13], v chetvertom - ispravlennaya temperatura yadra, v pyatom - elektronnaya temperatura tumannosti,
Tablica XIII
| Ob'ekt | T∗/1000 | Te/1000 | Izluchenie v nepreryvnom spektre | Vozbuzhdenie N1 i N2 | Stolknoveniya s atomami vodoroda |
W | |||
| metod "nebuliya" |
ispra- vlennaya |
||||||||
| NGC 7672 | 3,7 | 599 | 76 | 14 | 10 | 30 | 60 | 0,01 | 3 ⋅ 10-15 |
| NGC 7009 | 3,1 | 40 | 45 | 10 | 15 | 55 | 30 | 0,04 | 3 ⋅ 10-15 |
| NGC 6572 | 2,4 | 40 | 48 | 13 | 15 | 40 | 45 | 0,005 | 4 ⋅ 10-14 |
| NGC 6826 | 2,0 | 27 | 29 | 9 | 25 | 60 | 15 | 0,04 | 2 ⋅ 10-14 |
| JCII 4593 | 1,7 | 24 | 25 | 10 | 30 | 60 | 10 | 0,01 | 2 ⋅ 10-13 |
| NGC 6543 | 1,6 | 33 | 41 | 11 | 20 | 30 | 50 | 0,02 | 1 ⋅ 10-14 |
v shestom, sed'mom i vos'mom - dolya energii svobodnyh elektronov, rashoduemaya sootvetstvenno pri zahvatah i free-free transitions, pri stolknoveniyah s atomami OIII i pri stolknoveniyah s atomami vodoroda, v devyatom - velichina ![]() i, nakonec, v desyatom - koefficient dilyucii.
i, nakonec, v desyatom - koefficient dilyucii.
Iz rassmotreniya tabl. XIII mozhno sdelat' sleduyushie vyvody:
- Predpolozhenie Zanstra o perehode vsei energii svobodnyh elektronov v izluchenie linii "nebuliya" yavlyaetsya ves'ma grubym. Takim putem elektrony teryayut lish' okolopoloviny svoei energii. Sootvetstvenno etomu temperatury yader, opredelennye metodom "nebuliya", dolzhny byt' povysheny na neskol'ko tysyach ili dazhe desyatkov tysyach gradusov.
- Elektronnye temperatury planetarnyh tumannostei zaklyucheny v intervale 9000 - 14000°; . Strogo govorya, eti znacheniya yavlyayutsya verhnei granicei temperatur tumannostei, tak kak elektrony mogut teryat' energiyu eshe drugimi, ne uchtennymi nami sposobami. Dlya sravneniya privedem elektronnye temperatury tumannostei, poluchennye drugim metodom, a imenno - po otnosheniyu intensivnostei linii λ 4959 (N2) i λ 4363. Etot metod, vpervye ukazannyi V. A. Ambarcumyanom [14], byl primenen k tumannostyam Miyamoto [9] i Menzel [15]. Pervyi avtor poluchil temperatury v intervale 10000 - 25000°; , a vtoroi - v intervale 6000 - 10000°; . Rashozhdenie mezhdu etimi rezul'tatami obuslovleno trudnost'yu vychisleniya veroyatnostei neuprugih stolknovenii elektronov s atomami OIII.
Estestvenno dumat', chto elektronnye temperatury sovpadayut s temperaturami protonov i neitral'nyh atomov vodoroda. Odnako dlya tumannostei, rasshiryayushihsya s gradientom skorosti, Zanstra [8] ukazal odnu prichinu, kotoraya, po ego mneniyu, vedet k kraine nizkim skorostyam vodorodnyh atomov. Eta prichina - tormozhenie bystro letyashih atomov pri pogloshenii Lα-kvantov. Zanstra proizvel priblizhennyi podschet i poluchil, chto kazhdyi atom za vremya svoei neitral'noi zhizni dolzhen poteryat' pochti vsyu svoyu kineticheskuyu energiyu. Odnako, kak uzhe ukazyvalos', Zanstra poluchil nevernoe znachenie dlya plotnosti Lα-izlucheniya. Krome togo, on ne uchityval izlucheniya, idushego ot samih bystro letyashih atomov. Poetomu vyvod Zanstra yavlyaetsya oshibochnym. Bolee tochnye podschety (privodit' kotorye my zdes' ne budem) dokazyvayut, chto prakticheski temperatury elektronov, protonov i neitral'nyh atomov vodoroda mezhdu soboyu sovpadayut. Poetomu elektronnye temperatury, naidennye nami v etom paragrafe, yavlyayutsya temperaturami tumannostei v celom.
Otmetim eshe odin rezul'tat, vytekayushii iz sootnosheniya (37). Kak izvestno, nablyudennyi bal'merovskii dekrement neskol'ko bolee krut, chem teoreticheskii (vychislennyi Cillie). Znachitel'nuyu chast' etogo rashozhdeniya Berman [11] udalos' ob'yasnit' yavleniem prostranstvennogo pokrasneniya. Vse zhe v nekotoryh sluchayah rashozhdenie ostalos', i, vsledstvie etogo, Miyamoto [9] vydvinul gipotezu o vliyanii stolknovenii na bal'merovskii dekrement. My seichas pokazhem, chto eto vliyanie neznachitel'no.
Naidem otnoshenie chisla perehodov s pervogo urovnya na k-i pod vliyaniem stolknoveniya k chislu zahvatov na k-i. uroven'. Dlya vsei tumannosti eto otnoshenie, ochevidno, ravno ![]() . Ispol'zuya sootnoshenie (37), my mozhem napisat' sleduyushuyu cep' neravenstv:
. Ispol'zuya sootnoshenie (37), my mozhem napisat' sleduyushuyu cep' neravenstv:
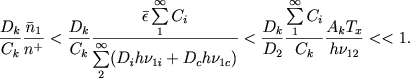
|
(59) |
Eti neravenstva deistvitel'no ustanavlivayut, chto stolknoveniya svobodnyh elektronov s vodorodnymi atomami ne mogut zametno izmenit' bal'merovskii dekrement, davaemyi rekombinacnonnoi teoriei (tochnee govorya, energiya, poluchaemaya elektronami pri fotoionizacii, nedostatochna dlya etogo). Na samom dele nebol'shie rashozhdeniya mezhdu teoriei i nablyudeniyami ob'yasnyayutsya, nevidimomu, neravnomernost'yu prostranstvennogo pokrasneniya.
V zaklyuchenie ostanovimsya na metodah dlya opredeleniya temperatur yader tumannostei. Krome metoda "nebuliya", o kotorom rech' shla vyshe, Zanstra razrabotal eshe bdin metod, dlya opredeleniya temperatur yader, kotoryi dlya kratkosti my nazovem metodom vodoroda. V osnove etogo metoda lezhit edinstvennoe predpolozhenie, chto tumannost' pogloshaet vse izluchenie, idushee ot zvezdy za granicei serii Laimana. Tak kak iz kazhdogo Lα-kvanta, pogloshennogo v tumannosti, voznikaet odin i tol'ko odin bal'merovskii kvant, to eto predpolozhenie privodit k sleduyushemu sootnosheniyu dlya opredeleniya temperatury yadra:
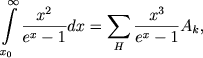
|
(60) |
gde summirovanie rasprostraneno na vsyu bal'merovskuyu seriyu (vklyuchaya kontinuum).
Kombiniruya sootnosheniya (56) i (60), Stoy [16] poluchil novyi metod dlya opredeleniya temperatur yader - po otnosheniyu intensivnostei linii "nebuliya" i bal'merovskoi serii vodoroda. Primenenie etogo metoda k tumannostyam i novym Zvezdam (Stoy [16], Page [13], Oehler 18) privelo k znachitel'no bolee nizkim temperaturam, chem poluchennye metodam Zanstra. Pol'zuyas' vysheprivedennymi formulami, my mozhem seichas vyskazat' sleduyushie soobrazheniya o vseh perechislennyh metodah dlya opredeleniya temperatur yader tumannostei.
-
Pri prakticheskom primenenii metoda vodoroda bol'shie trudnosti voznikayut pri opredelenii velichin Ak dlya linii Nα i dlya bal'merovekogo kontinuuma. Odnako trudnosti legko oboiti, esli uchest' rezul'taty raboty Cillie. Tak kak otnoshenie chisla kvantov, izluchaemyh tumannostyami v linii Nβ, k obshemu chislu bal'merovskih kvantov ravno
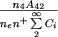 , to vmesto sootnosheniya (60) my poluchaem
, to vmesto sootnosheniya (60) my poluchaem
gde velichiny Aβ i h v pravoi chasti otnosyatsya k linii Nβ. Dlya opredeleniya temperatury yadra iz etogo sootnosheniya tochnogo znacheniya Te ne trebuetsya, tak kak velichina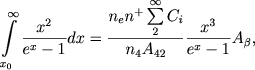
(61) 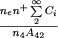 pochti ne menyaetsya s Te (mozhno prinyat', chto eta velichina ravno 9,2).
pochti ne menyaetsya s Te (mozhno prinyat', chto eta velichina ravno 9,2).
- Metod "nebuliya", osnovannyi na dopushenii, chto vsya energiya svobodnyh elektronov perehodit v izluchenie linii "nebuliya", daet, ochevidno, nizhnyuyu granicu temperatury yadra. Kak bylo vyyasneno, posle utochneniya etogo metoda, temperatura yadra dolzhna opredelyat'sya iz sootnosheniya (58). No podstavlyaya v eto sootnoshenie znacheniya A i S iz formul (42) i (44), my vidim, chto ono prevrashaetsya v sootnoshenie (61). Eto oznachaet, chto utochnennyi metod "nebuliya" ekvivalenten metodu vodoroda. Fizicheski takoi rezul'tat vpolne ponyaten, ibo oba metoda Zanstra osnovany na sravnenii odnih i teh zhe uchastkov nepreryvnogo spektra zvezdy (vidimogo i za granicei serii Laimana).
-
Esli v pravoi chasti sootnosheniya (46) prenebrech' pervym i tret'im chlenami, to my pridem k uravneniyu
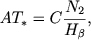
(62) kotoroe sootvetstvuet metodu Stoy. Vpolne ponyatno, chto pri opredelenii temperatur yader iz uravneniya (62) dolzhny poluchat'sya ves'ma nizkie znacheniya.
Takim obrazom my prihodim k sleduyushemu vyvodu: temperatury yader tumannostei dolzhny opredelyat'sya metodom vodoroda, t. e. iz uravnenii (60)) ili (61); posle etogo temperatury samih tumannostei mogut byt' naideny iz uravneniya (46).
Mozhno, odnako, ukazat' druguyu tochku zreniya. Esli temperatury tumannostei, opredelennye Menzel po otnosheniyu intensivnostei linii λ 4959 i λ 4363, pravil'ny, to v sootnoshenii (46) poslednii chlen okazyvaetsya malym, i eto sootnoshenie prinimaet vid
|
|
(63) |
Odnako temperatury yader, opredelennye iz uravneniya (63), budut znachitel'no nizhe temperatur, opredelennyh iz uravneniya (60). Eto protivorechie mozhno ustranit', esli sdelat' predpolozhenie, chto raspredelenie energii v spektre yadra sil'no otlichaetsya ot raspredeleniya Planka. V takom sluchae uravnenie (60) daet cvetovuyu temperaturu, harakterizuyushuyu otnoshenie intensivnostei v vidimoi chasti spektra zvezdy i za granicei serii Laimana, a uravnenie (63) - temperaturu, harakterizuyushuyu raspredelenie energii za granicei serii Laimana. Sootnoshenie (46) daet v etom sluchae verhnyuyu granicu temperatury tumannosti.
<< 3.2 Pole Lα-izlucheniya | Oglavlenie | Glava IV. Obolochki novyh zvezd >>
|
Publikacii s klyuchevymi slovami:
obolochki zvezd - perenos izlucheniya
Publikacii so slovami: obolochki zvezd - perenos izlucheniya | |
|
Sm. takzhe:
| |