Astronet > Dvizhushiesya obolochki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Dvizhushiesya obolochki zvezd << Glava IV. Obolochki novyh zvezd | Oglavlenie | 4.2 Real'nyi atom >>

4.1 Atom s tremya urovnyami

V etom paragrafe chislo ionizovannyh atomov my budem oboznachat' cherez n₃ (vmesto n⁺), a pod statisticheskim vesom tret'ego sostoyaniya budem ponimat' velichinu

$g_3 = g^+\frac{(2\pi mkT)^{\frac{3}{2}}}{n_e h^3} .$ (1)

Naryadu s shirinoi spektral'noi linii Δν_₁₂ my vvedem effektivnye shiriny Δν_₁₃ i Δν_₂₃ . Togda formal'no tretii uroven' nichem ne budet otlichat'sya ot pervyh dvuh. Raznica mezhdu nimi budet tol'ko ta, chto dlya izlucheniya s chastotoi ν_₁₂ budet imet' znachenie effekt Doplera, a dlya izlucheniya s chastotami ν_₁₃ i ν_₂₃ - ne budet.

Usloviya luchevogo ravnovesiya my poluchim iz uslovii costoyanstva chisla atomov v kazhdom iz sostoyanii. Dlya pervogo i tret'ego sostoyanii eti usloviya imeyut vid:

$\left. \begin{array}{l} n_1 B_{12}\rho_{12} + n_1 B_{13}\rho_{13} = n_2 A_{21} + n_3 A_{31} \\ n_1 B_{13}\rho_{13} + n_2 B_{23}\rho_{23} = n_3 A_{31} + n_3 A_{32} \end{array} \right\}$ (2)

Zdes' my prenebregli perehodami, vyzvannymi stolknoveniyami, a takzhe einshteinovskim otricatel'nym poglosheniem. Vvedem teper' velichiny, obychno upotreblyaemye v teorii luchevogo ravnovesiya. Pust' a_ik - ob'emnyi koefficient poglosheniya, J_ik - intensivnost' izlucheniya, ε_ik - kolichestvo energii, izluchaemoe 1 sm³ za 1 sek. v edinichnom telesnom ugle.

My imeem

$a_{ik} = \frac{n_i B_{ik} h\nu_{ik}}{c\Delta \nu_{ik}} ,$ (3)

$\rho_{ik} = \frac{1}{c} \int J_{ik} d\omega ,$ (4)

$4\pi\epsilon_{ik}\Delta\nu_{ik} = n_k A_{ki} h\nu_{ik} ,$ (5)

i uravneniya (2) mogut byt' perepisany v vide:

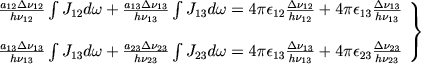
$\left. \begin{array}{l} \frac{a_{12}\Delta\nu_{12}}{h\nu_{12}}\int J_{12} d\omega + \frac{a_{13}\Delta\nu_{13}}{h\nu_{13}}\int J_{13} d\omega = 4\pi\epsilon_{12}\frac{\Delta\nu_{12}}{h\nu_{12}} + 4\pi\epsilon_{13}\frac{\Delta\nu_{13}}{h\nu_{13}} \\ \\ \frac{a_{13}\Delta\nu_{13}}{h\nu_{13}}\int J_{13} d\omega + \frac{a_{23}\Delta\nu_{23}}{h\nu_{23}}\int J_{23} d\omega = 4\pi\epsilon_{13}\frac{\Delta\nu_{13}}{h\nu_{13}} + 4\pi\epsilon_{23}\frac{\Delta\nu_{23}}{h\nu_{23}} \end{array} \right\}$ (6)

Estestvenno vvesti zdes' velichiny K_ik i C_ik, ravnye

$K_{ik} = J_{ik}\frac{\Delta\nu_{ik}}{h\nu_{ik}}, \quad C_{ik} = \epsilon_{ik}\frac{\Delta\nu_{ik}}{h\nu_{ik}}.$ (7)

Krome togo, polozhim

$\frac{a_{13}}{a_{12}} = \frac{B_{13}\nu_{13}\Delta\nu_{12}}{B_{12}\nu_{12}\Delta\nu_{13}} = q,$ (8)

$\frac{a_{13}C_{13}}{a_{23}C_{23}}=\frac{A_{31}}{A_{32}}=\frac{p}{1-p} .$ (9)

Togda vmesto (6) poluchaem

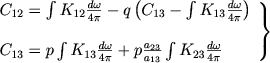
$\left. \begin{array}{l} C_{12}=\int K_{12}\frac{d\omega}{4\pi} - q\left(C_{13}-\int K_{13}\frac{d\omega}{4\pi}\right) \\ \\ C_{13}=p\int K_{13}\frac{d\omega}{4\pi} + p\frac{a_{23}}{a_{13}}\int K_{23}\frac{d\omega}{4\pi} \end{array} \right\}$ (10)

Tak kak otnoshenie a₂₃/a₁₃ proporcional'no velichine C₁₂, to, voobshe govorya, vtoroe iz etih uravnenii yavlyaetsya nelineinym. Odnako my uzhe uslovilis' schitat', chto opticheskaya tolshina obolochki v chastote ν_₂₃ men'she edinicy. Poetomu velichinu ρ_₂₃ mozhno schitat' postoyannoi.

S pomosh'yu vysheprivedennyh formul legko nahodim

$\frac{a_{23}}{a_{13}}\int K_{23}\frac{d\omega}{4\pi} = \frac{g_3}{g_2}\frac{A_{32}}{A_{21}}\frac{W\rho_{23}}{q}C_{12} ,$ (11)

gde ispol'zovano odno iz obychnyh oboznachenii:

$\sigma_{ik} = \frac{8\pi h\nu_{ik}}{c^3}, \quad \bar \rho_{ik} = \frac{1}{e^{\frac{h\nu_{ik}}{kT}}-1}.$ (12)

Vvedem eshe sleduyushee oboznachenie:

$\gamma = 3p\frac{g_3}{g_2}\frac{A_{32}}{A_{21}}W\bar \rho_{23} .$ (13)

Togda, podstavlyaya (11) v (10), okonchatel'no poluchaem

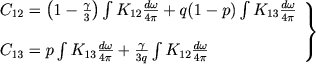
$\left. \begin{array}{l} C_{12}=\left(1-\frac{\gamma}{3}\right)\int K_{12}\frac{d\omega}{4\pi} + q(1-p)\int K_{13}\frac{d\omega}{4\pi} \\ \\ C_{13}=p\int K_{13}\frac{d\omega}{4\pi} + \frac{\gamma}{3q}\int K_{12}\frac{d\omega}{4\pi} \end{array} \right\}$ (14)

Takovy usloviya luchevogo ravnovesiya nashei zadachi.

Vvedem opticheskie rasstoyaniya ot vnutrennei granicy obolochki v chastotah ν_₁₂ i ν_₁₃:

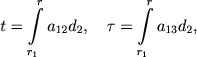
$t=\int\limits_{r_1}^r a_{12}d_2, \quad \tau=\int\limits_{r_1}^r a_{13}d_2,$ (15)

gde r₁ i r sut' rasstoyaniya vnutrennei granicy obolochki i dannogo sloya ot zvezdy. Oboznachim cherez θ ugol mezhdu napravleniem izlucheniya i napravleniem vneshnei normali k sloyu.

Togda uravnenie perenosa izlucheniya v chastote ν_₁₃ budet imet' obychnyi vid

$\cos\theta\frac{dK_{13}}{d\tau} = C_{13} - K_{13} .$ (16)

No dlya izlucheniya v chastote ν_₁₂, dlya kotorogo igraet rol' effekt Doplera, v predydushei glave my poluchili bolee slozhnoe uravnenie (III, 17). Schitaya, chto velichina β mala, vmesto uravneniya (III, 17) priblizhenno nahodim

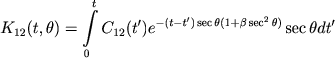
$K_{12}(t,\theta) = \int\limits_0^t C_{12}(t')e^{-(t-t')\sec\theta (1+\beta\sec^2\theta)}\sec\theta dt'$ (17)

Otsyuda poluchaetsya sleduyushee uravnenie perenosa izlucheniya v chastote ν_₁₂:

$\cos\theta\frac{dK_{12}}{dt} = -(1+\beta\cos^2\theta)K_{12} + C_{12} .$ (18)

Takim obrazom nasha zadacha svoditsya k resheniyu uravnenii (14), (16) i (18).

V predydushei glave, rassmatrivaya luchevoe ravnovesie planetarnoi tumannosti v chastote ν_₁₂, my sostavili integral'noe uravnenie dlya velichiny C₁₂. Teper', dlya prostoty, my predpochli poluchit' uravnenie perenosa (18) i reshim zadachu obychnym metodom Eddingtona.

Vvedem sleduyushie oboznacheniya:

$\bar K_{ik} = \int K_{ik}\frac{d\omega}{4\pi}, \quad H_{ik} = \int K_{ik}\cos\theta\frac{d\omega}{4\pi}.$ (19)

Iz uravnenii (16) i (18) nahodim:

$\frac{dH_{13}}{d\tau} = C_{13} - \bar K_{13}, \quad \frac{dH_{12}}{dt} = C_{12} -(1+\frac{\beta}{3})K_{12},$ (20)

$\frac{d\bar K_{13}}{d\tau} = -3H_{13}, \quad \frac{d\bar K_{12}}{dt} = -3H_{12}.$ (21)

(V poslednem uravnenii my prenebregali velichinoi β po sravneniyu s edinicei). Eti uravneniya s pomosh'yu (14) dayut:

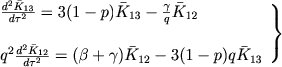
$\left. \begin{array}{l} \frac{d^2\bar K_{13}}{d\tau^2} = 3(1-p)\bar K_{13}-\frac{\gamma}{q}\bar K_{12} \\ \\ q^2\frac{d^2\bar K_{12}}{d\tau^2} = (\beta +\gamma )\bar K_{12}-3(1-p)q\bar K_{13} \end{array} \right\}$ (22)

Obshee reshenie sistemy uravnenii (22) imeet vid

$\bar K_{13} = Ae^{\lambda_1 \tau} + Be^{-\lambda_1 \tau}Ce^{\lambda_2 \tau} + De^{-\lambda_2 \tau}$ (23)

$\begin{array}{l} \bar K_{12} = \frac{q}{\gamma}[3(1-p)-\lambda_1^2](Ae^{\lambda_1 \tau} + Be^{-\lambda_1 \tau}) + \\ +\frac{q}{\gamma}[3(1-p)-\lambda_2^2](Ce^{\lambda_2 \tau} + De^{-\lambda_2 \tau}), \end{array}$ (24)

gde λ₁ i λ₂ sut' korni uravneniya

$[\lambda^2-3(1-p)][q^2 \lambda^2 - (\beta + \gamma)]=3(1-p)\gamma,$ (25)

a A, B, C, D - proizvol'nye postoyannye

V dal'neishem my budem schitat', chto

$\beta >> q^2 .$ (26)

Tak kak velichina q² ochen' mala (poryadka 10^-8), to eto uslovie yavlyaetsya vypolnennym dlya lyuboi obolochki.

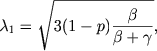
$\lambda_1 = \sqrt{3(1-p)\frac{\beta}{\beta + \gamma}} ,$ (27)

$\lambda_2 = \frac{1}{q}\sqrt{\beta + \gamma}$ (28)

i vmesto (24) imeem

$\bar K_{12} = \frac{3(1-p)q}{\beta + \gamma} (Ae^{\lambda_1 \tau} + Be^{-\lambda_1 \tau}) - \frac{\beta + \gamma}{q\gamma} (Ce^{\lambda_2 \tau} + De^{-\lambda_2 \tau}) .$ (29)

Chtoby naiti proizvol'nye postoyannye A, V, S, D, nado zadat' granichnye usloviya. Eti usloviya my zadaem v vide

$\left. \begin{array}{lr} 2H_{12} = \bar K_{12},\; 2H_{13} = \bar K_{13} & (pri\; \tau=\tau_0) \\ 2H_{12} + \bar K_{12} = 0,\; H_{13} = \frac{1}{4} S_{13} & (pri\; \tau=0) \end{array} \right\}$ (30)

Velichina πS₁₃, t.e. chislo kvantov v chastote ν_₁₃, padayushih ot zvezdy na vnutrennyuyu granicu obolochki, ravna

$\pi S_{13} = W\sigma_{13}\bar \rho_{13} c\frac{\Delta\nu_{13}}{h\nu_{13}} .$ (31)

Naibol'shii interes predstavlyaet sluchai, kogda opticheskaya tolshina obolochki v chastote ν_₁₃ znachitel'no prevoshodit edinicu (τ₀ > 1). V chtom sluchae dlya srednih chastei obolochki my legko poluchaem

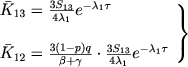
$\left. \begin{array}{l} \bar K_{13} = \frac{3S_{13}}{4\lambda_1}e^{-\lambda_1 \tau} \\ \\ \bar K_{12} = \frac{3(1-p)q}{\beta + \gamma} \cdot \frac{3S_{13}}{4\lambda_1}e^{-\lambda_1 \tau} \end{array} \right\}$ (32)

(tak kak ostal'nye chleny, vhodyashie v vyrazheniya dlya $\bar K_{13}$ i $\bar K_{12}$ , igrayut lish' rol' popravok vblizi granic). Podstavlyaya (32) v (14), dlya C₁₂ i C₁₃ nahodim

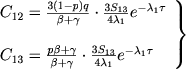
$\left. \begin{array}{l} C_{12} = \frac{3(1-p)q}{\beta + \gamma} \cdot \frac{3S_{13}}{4\lambda_1}e^{-\lambda_1 \tau} \\ \\ C_{13} = \frac{p\beta + \gamma}{\beta + \gamma} \cdot \frac{3S_{13}}{4\lambda_1}e^{-\lambda_1 \tau} \end{array} \right\}$ (33)

Znanie velichin C₁₂ i C₁₃ pozvolyaet naiti stepen' vozbuzhdeniya i ionizacii v obolochke, t. e. velichiny n₂/n₁ i n₃/n₁. Na osnovanii sootnoshenii (3), (5) i (7), my imeem

$\frac{n_i}{n_1} = \frac{4\pi}{c}\frac{B_{1i}}{A_{i1}}\frac{h\nu_{1i}}{\Delta\nu{_{1i}}} C_{1i}$ (34)

i, podstavlyaya (33) v (34) nahodim

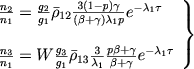
$\left. \begin{array}{l} \frac{n_2}{n_1} = \frac{g_2}{g_1}\bar \rho_{12} \frac{3(1-p)\gamma}{(\beta + \gamma) \lambda_1 p} e^{-\lambda_1 \tau} \\ \\ \frac{n_3}{n_1} = W\frac{g_3}{g_1}\bar \rho_{13}\frac{3}{\lambda_1}\frac{p\beta + \gamma}{\beta + \gamma} e^{-\lambda_1 \tau} \end{array} \right\}$ (35)

Oboznachim

$\beta = z\gamma .$ (36)

Togda formuly (35) preobrazuyutsya k vidu

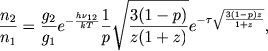
$\frac{n_2}{n_1} = \frac{g_2}{g_1}e^{-\frac{h\nu_{12}}{kT}}\frac{1}{p} \sqrt{\frac{3(1-p)}{z(1+z)}}e^{-\tau \sqrt{\frac{3(1-p)z}{1+z}}} ,$ (37)

$\frac{n_3}{n_1} n_e = W\frac{g^+}{g_1} \frac{(2\pi mkT)^{\frac{3}{2}}}{h^3} e^{-\frac{h\nu_{13}}{kT}} \frac{3(1+pz)}{\sqrt{3(1-p)z(1+z)}}e^{-\tau \sqrt{\frac{3(1-p)z}{1+z}}} ,$ (38)

Eti formuly yavlyayutsya dlya nas okonchatel'nymi. Otmetim, chto v sluchae nepodvizhnoi obolochki t. e. pri β = 0, velichiny $\bar K_{12}$ i $\bar K_{13}$ , a znachit, i velichiny n₂/n₁ i n₃/n₁, yavlyayutsya ne eksponencial'nymi, kak poluchilos' u nas, a lineinymi funkciyami ot opticheskogo rasstoyaniya.

Do sih por schitalos', chto v nebulyarnyh obolochkah stepen' vozbuzhdeniya i ionizacii zavisit ot treh velichin: ot temperatury zvezdy, ot koefficienta dilyucii i ot plotnosti materii. Teper' my vidim, chto ona zavisit takzhe - i pritom ves'ma sil'no - ot sostoyaniya dvizheniya obolochki. Chem bol'she gradient skorosti v obolochke, tem men'she stepen' vozbuzhdeniya i ionizacii i tem bystree ona padaet pri perehode ot vnutrennei granicy obolochki k vneshnei.

<< Glava IV. Obolochki novyh zvezd | Oglavlenie | 4.2 Real'nyi atom >>

Publikacii s klyuchevymi slovami: obolochki zvezd - perenos izlucheniya Publikacii so slovami: obolochki zvezd - perenos izlucheniya
Sm. takzhe: Sbrasyvayushaya massivnuyu obolochku zvezda G79.29+0.46 Obnaruzhenie goryachego vodyanogo para v obolochke uglerodnoi zvezdy. Obolochki v tumannosti Yaico Osveshennost' Planetarnye tumannosti

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\frac{dH_{13}}{d\tau} = C_{13} - \bar K_{13}, \quad \frac{dH_{12}}{dt} = C_{12} -(1+\frac{\beta}{3})K_{12},$	(20)
$\frac{d\bar K_{13}}{d\tau} = -3H_{13}, \quad \frac{d\bar K_{12}}{dt} = -3H_{12}.$	(21)

$\lambda_1 = \sqrt{3(1-p)\frac{\beta}{\beta + \gamma}} ,$	(27)
$\lambda_2 = \frac{1}{q}\sqrt{\beta + \gamma}$	(28)